2. 山东理工大学 机械工程学院, 山东 淄博 255049
针对滚动轴承状态监控中最优共振频带难确定的问题,提出一种新的寻优方法和目标函数,可快速准确地定位共振频带,提取状态信息.通过两步网格搜索法,以包络稀疏性为目标函数,对Gabor滤波器参数寻优;然后对振动信号进行滤波并得到信号包络;最后运用包络自相关谱抑制噪声,突出运行状态信息.用仿真信号和实际信号对该方法进行了验证,结果表明,该方法能准确判明轴承运行状态.
2. School of Mechanical Engineering, Shandong University of Technology, Shandong Zibo 255049, China
Aiming to the difficulty in finding the resonant frequency band in condition monitoring of rolling element bearings, a new optimization method and objective function was proposed. The resonant frequency band can be located through this proposed method. Firstly, the parameters of Gabor filter are optimized through the two-step grid search method, in which the envelope sparseness is as objective function. The vibration signal was filtered through the optimal filter and the envelop signal was calculated. The envelop autocorrelation spectrum was adopted to restrain noise and highlight operation condition information. The effectiveness and advantages of the proposed method were proved through the simulation signal and experimental signals. It is shown that the bearing operation condition can be recognized accurately by the proposed method.
滚动轴承是旋转机械中常用的支撑部件,超过30%的旋转机械故障与轴承故障有关. 基于振动信号分析的滚动轴承运行状态监控与故障诊断方法是近年来的研究热点[1, 2]. 包络分析(又称共振解调)是应用广泛且有效的滚动轴承振动信号处理技术之一,其难点在于确定共振解调频带,近来很多学者做了大量研究[3, 4, 5]. 笔者提出两步网格搜索法,以包络稀疏性为目标函数,对Gabor滤波器参数寻优. 然后运用Gabor滤波器对振动信号进行滤波,最后运用包络自相关谱抑制噪声,突出运行状态信息. 通过仿真信号和实际信号对该方法进行了验证.
1 Gabor滤波器与参数优化 1.1 Gabor滤波器Gabor滤波器[6]因为具有良好的时频局部化特性,易于调整基频带宽及中心频率从而能够很好地兼顾信号在时域和频域中的分辨能力. 一维Gabor滤波器是高斯包络下的单频率复正弦函数,定义为
| $g\left( t \right) = {{\text{e}}^{ - \frac{{{t^2}}}{{2{\sigma ^2}}}}}{{\text{e}}^{{\text{j}}2\pi {f_c}t}}/\sqrt {2\pi } \sigma $ | (1) |
其中:σ为高斯包络宽度参数,fc为中心频率. 为分析方便,利用2σ2=1/β2将式(1)改写成下面的形式,其中式(2)的频域为式(3).
| $\left. {g\left( t \right) = \frac{\beta }{{\sqrt \pi }}{\text{e}}} \right|{}^{ - {\beta ^2}{t^2}}{{\text{e}}^{{\text{j}}2\pi {f_{\text{c}}}t}}$ | (2) |
| $G\left( f \right) = {{\text{e}}^{\left( { - {\pi ^2}/{\beta ^2}} \right){{\left( {f - {f_{\text{c}}}} \right)}^2}}}$ | (3) |
其中带宽参数β和中心频率fc共同影响Gabor滤波器的形状. 假设信号x(t),其傅里叶变换是X(f),则Gabor滤波器对x(t)滤波后的信号为
| $W\left( t \right) = {F^{ - 1}}\left[{\begin{array}{*{20}{c}} {X\left( f \right)}&{G\left( f \right)} \end{array}} \right]$ | (4) |
其中F-1[·]表示逆傅里叶变换.
1.2 网格搜索与目标函数网格搜索是将待搜索参数划分成一定空间范围的网格,通过逐步计算网格中所有点的目标函数来确定最优参数. 针对传统网格搜索法搜索时间长的问题提出一种两步的网格搜索法,先以较大步长在参数空间内进行粗搜索,初步确定一个近似最优参数区间,然后在此小区间内进行精搜索,大幅度地减少了参数寻优时间,更好地满足在线状态监控的要求. 对共振频带解调而言,频率中心的重要性要高,可将频率中心的网格设置得密一些,带宽设置得疏一些.
峭度是在旋转机械状态监控中广泛应用的一个统计量,但是峭度对于随机冲击噪声非常敏感. 笔者用稀疏性作为目标函数,因为其对随机冲击具有一定鲁棒性. 稀疏性指标公式为
| $\begin{gathered} {\text{Sp}}\left( x \right) = \sqrt {\frac{1}{N}\sum\limits_{n = 1}^N {{x^2}\left( n \right)} } /\sqrt {\frac{1}{N}\sum\limits_{n = 1}^N {\left| {x\left( n \right)} \right|} } = \\ \sqrt N \frac{{{{\left\| x \right\|}_2}}}{{{{\left\| x \right\|}_1}}} \\ \end{gathered} $ | (5) |
其中N为信号x的长度. 网格搜索法搜寻滤波器参数可表达为
| ${P_{{\text{optimal}}}} = {\arg _{\left( {{f_{\text{c}}},\beta } \right)}}\max \left\{ {{\text{Sp}}\left[{{\text{env}}\left( {{\text{G}}{{\text{F}}_{\left( {{f_{\text{c}}},\beta } \right)}}\left( x \right)} \right)} \right]} \right\}$ | (6) |
其中:GF(fc,β)(x)表示参数为fc和β的Gabor滤波器对信号x进行滤波后得到的信号,env(·)表示滤波后信号的包络.
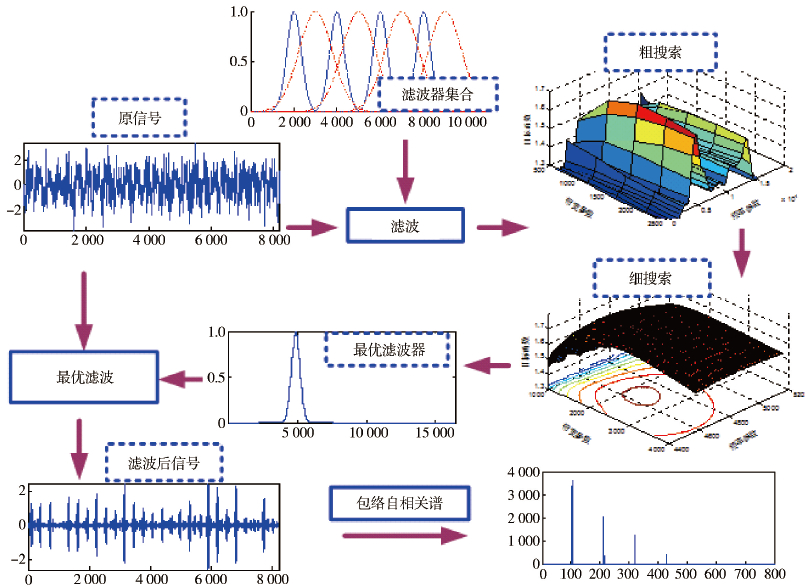
1.3 方法流程基于以上分析,提出通过两步网格搜索法,以包络稀疏性为目标函数,对滤波器参数寻优. 然后对振动信号进行滤波并得到信号包络,最后进行包络自相关谱分析. 所提出方法的流程如图 1所示,具体步骤如下.
1) 粗搜索:为减小轴转频及谐波的干扰,并考虑到采样定理,将中心频率的范围设定为(40fr~ fs/2.5)区间,形成等分的50个搜索网格. 其中,fr为轴承的旋转频率,fs为振动传感器采样频率. 假设fstep为粗搜索阶段网格间距,经过粗搜索阶段得到最优频率中心fcoarse. 将带宽参数网格设定为(3、6、9、12、15)倍的fi,其中fi为内圈特征频率.
2) 细搜索:将中心频率的范围设定为 (fcoarse± fstep/2)区间,形成等分的50个搜索网格. 将带宽参数范围设定为(3~15) fi,布置50个搜索网格.
3) 最优滤波:以粗-细网格搜索得到的最优滤波器对信号进行滤波,得到滤波后信号sOF(t).
4) 求取包络:信号 sOF(t) 包络的计算公式如式(7)所示,其中HT[·]表示希尔伯特变换.
| ${\text{env}}\left( t \right) = \sqrt {{s_{{\text{OF}}}}{{\left( t \right)}^2} + {{\left( {HT\left[{{s_{{\text{OF}}}}\left( t \right)} \right]} \right)}^2}} $ | (7) |
5) 包络自相关谱分析:为有效地抑制噪声,突出故障特征,求取env(t)的自相关为
| ${R_{xx}}\left( m \right) = E\left[{{\text{env}}\left( t \right){\text{env}}\left( {t - m} \right)} \right],m = 0,1,\cdots ,N - 1$ | (8) |
其中m为延迟.
对式(8)求其傅里叶变换:
| ${R_{xx}}\left( f \right) = F\left[{{R_{xx}}\left( m \right)} \right]$ | (9) |
分析Rxx(f)中故障特征频率成分信息即可对轴承运行状态做出判断.
2 仿真验证根据轴承外圈单点损伤的理论模型,仿真外圈故障振动信号. 仿真信号x(t)的模型为
| $\left. \begin{gathered} x\left( t \right) = \sum\limits_i {{A_i}s\left( {t - iT - {\tau _i}} \right)} \hfill \\ {A_i} = {A_1}\cos \left( {2\pi {f_{\text{M}}}t} \right) + {A_2} \hfill \\ s\left( t \right) = {{\text{e}}^{ - \zeta t}}\sin \left( {2\pi {f_{{\text{n}}1}}t + 2\pi {f_{{\text{n}}2}}t} \right) \hfill \\ \end{gathered} \right\}$ | (10) |
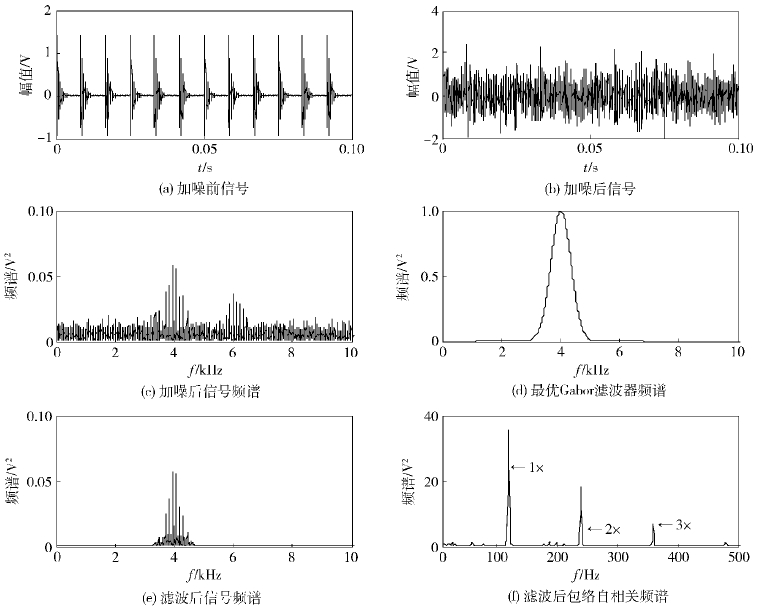
其中:s(t)是指数衰减的正弦振动信号,冲击间隔时间为T;Ai是调幅系数信号,频率为fM,A2为常数 (A2>A1);τi用于模拟随机滑动;ζ为阻尼系数;fn1和fn2为系统的两个共振频率. 根据式(10),模拟信号参数:采样频率为20 kHz,系统的两个共振频率为4 kHz和6 kHz,轴转频为30 Hz,ζ=0.05,故障频率为100 Hz. 图 2给出了仿真信号的分析过程.
图 2(a)为模拟单点故障信号,图 2(b)为加入正态分布的噪声(信噪比为-12 dB)后的信号. 图(c)为加入噪声后的频谱,从中可以看出4 kHz和6 kHz的共振带. 图 2(d)为经过粗-细搜索得到的最优Gabor滤波器的频谱,fc=4.030 kHz,β=1 500. 图 2(e)为仿真故障信号经过最优Gabor滤波器滤波后的信号频谱,可以看出确定了4 kHz的主要共振频带. 图 2(f)为滤波后信号的自相关包络频谱,可以看到清晰的故障频率及其谐波. 寻优后所得的中心频率4.030 kHz与仿真信号中的固有共振频率4 kHz基本吻合,充分说明了所提方法确定共振频带的有效性.
3 实测信号验证 3.1 实验台与数据采集为验证所提方法的有效性,在加拿大湖首大学智能机电系统实验室[7]的滚动轴承实验台上采集了多种常见运行状态下的振动信号,如外圈故障、内圈故障、滚动体故障和正常运行.
实验轴承为单列深沟球轴承,型号为MB ER-10K,其主要结构参数:节径为33.50 mm,滚动体数目为8,滚动体直径为7.94 mm,接触角为0°. 在转速为2 100 r/min的情况下,实验轴承的理论故障特征频率:外圈故障特征频率fo=107 Hz,内圈故障特征频率fi=173 Hz,滚动体故障特征频率fb=139 Hz. 采样频率设定在32 768 Hz.
3.2 方法对比为了验证所提方法的有效性,与轴承故障诊断领域中经典的包络分析法以及快速谱峭度图法进行了对比分析.
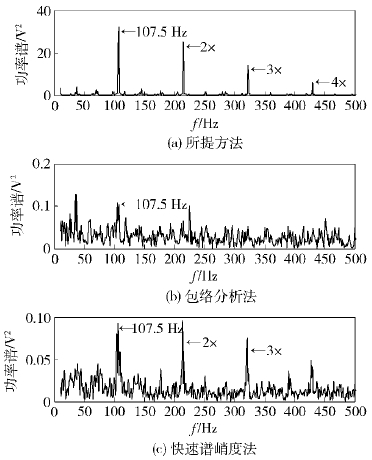
图 3为外圈故障信号的对比分析结果. 从图 3(a)中可以清晰地看到外圈故障特征频率107.5 Hz以及2~4次谐波,说明发生了外圈故障. 从图 3(b)中只可以看到外圈故障特征频率,无法看到其他谐波,说明普通的包络分析效果没有所提方法好. 虽然以峭度最大为目标的快速谱峭度图法也能发现外圈故障频率及其谐波,但是频谱噪声明显比所提方法要大很多.
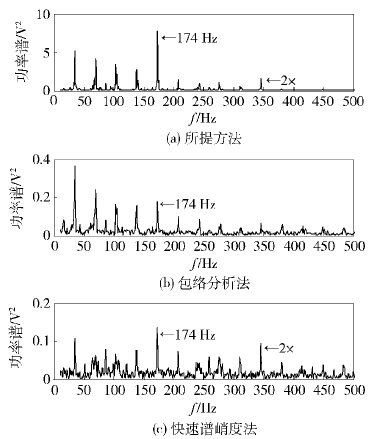
图 4为内圈故障信号的对比分析结果. 从图 4(a)中可以清晰地看到内圈故障特征频率174 Hz以及2次谐波. 从图 4(b)中虽然可看到内圈故障特征频率,但是该频率在谱图上不是主导成分,可能会导致诊断误判. 同样,图 4(c)中快速谱峭度图法也能发现故障频率,但是频谱粗糙,没有所提方法信噪比高.
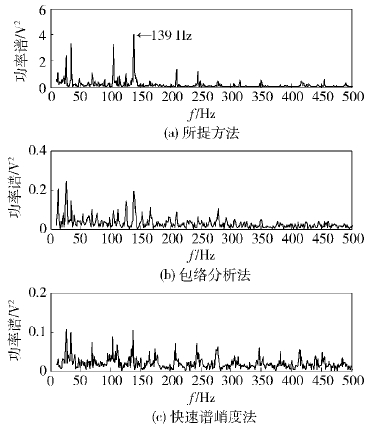
图 5为滚动体故障信号的对比分析结果. 从图 5(a)中可以看到滚动体故障特征频率139 Hz. 虽然从图 5(b)中也能看到故障特征频率成分,但其在频谱图上不是主导成分. 快速谱峭度图法只发现了轴的转频成分,无法判断故障信息.
4 结束语针对旋转机械运行状态特征提取困难问题,提出了基于最优Gabor滤波器的轴承状态监控方法. 以包络稀疏性为目标函数,通过粗-细网格法对Gabor滤波器参数寻优,有效地确定了富含运行状态信息的共振频带. 运用包络自相关谱抑制噪声,突出了运行状态信息. 通过仿真信号和实验台信号验证了所提方法的有效性及优点.
| [1] | 许同乐, 侯蒙蒙, 蔡道勇, 等. FastICA遗传神经网络算法[J]. 北京邮电大学学报, 2014, 37(4):25-28. Xu Tongle, Hou Mengmeng, Cai Daoyong, et al. FastICA genetic neural networks method[J]. Journal of Beijing University of Posts and Telecommunications, 2014, 37(4):25-28.[引用本文:1] |
| [2] | 雷亚国, 韩冬, 林京, 等. 自适应随机共振新方法及其在故障诊断中的应用[J]. 机械工程学报, 2012, 48(7):62-67. Lei Yaguo, Han Dong, Lin Jing, et al. New adaptive stochastic resonance method and its application to fault diagnosis[J]. Chinese Journal of Mechanical Engineering, 2012, 48(7):62-67.[引用本文:1] |
| [3] | Antoni J. Fast computation of the kurtogram for the detection of transient faults[J]. Mechanical Systems and Signal Processing, 2007, 27(1):108-124.[引用本文:1] |
| [4] | 丁康, 黄志东, 林慧斌. 一种谱峭度和Morlet小波的滚动轴承微弱故障诊断方法[J]. 振动工程学报, 2014, 27(1):128-135. Ding Kang, Huang Zhidong, Lin Huibin. A weak fault diagnosis method for rolling element bearings based on Morlet wavelet and spectral kurtosis[J]. Journal of Vibration Engineering, 2014, 27(1):128-135.[引用本文:1] |
| [5] | Wang Dong, Tse P W, Tsui K L. An enhanced Kurtogram method for fault diagnosis of rolling element bearings[J]. Mechanical Systems and Signal Processing, 2013, 35(1):176-199.[引用本文:1] |
| [6] | 刘军, 景晓军, 孙松林, 等. 一种用于人脸识别的基于主导近邻像素的局部Gabor空间直方图特征[J]. 北京邮电大学学报, 2015, 38(1):51-54. Liu Jun, Jing Xiaojun, Sun Songlin, et al. Feature of local Gabor spatial histogram based on dominant neighboring pixel for face recognition[J]. Journal of Beijing University of Posts and Telecommunications, 2015, 38(1):51-54.[引用本文:1] |
| [7] | Sui Wentao, Shazali O, Wang Wilson. An adaptive envelope spectrum technique for bearing fault detection[J]. Measurement Science and Technology, 2014, 25(9):1-9.[引用本文:1] |