2. 甘肃中医药大学 定西校区 数学系, 甘肃 定西 743000
针对内点算法求解半定规划进行三维无线传感器网络定位无法满足实际的需求,利用变量变换将半定规划问题转换为非线性规划问题,提出了解决非线性规划化问题的可行方向算法.在此基础上,取非线性规划问题变量的列数为3,阻止高秩解的产生.为了进一步提高计算效率,采用限制未知节点的度对三维网络图进行稀疏.仿真结果表明,可行方向算法是行之有效的,而且计算速度优于已有的稀疏半定规划内点算法.
2. Department of Mathematics of Dingxi Campus, Gansu University of Chinese Medicine, Gansu Dingxi 743000, China
By using the change of variables, the semidefinite programming (SDP) problem for solving the senor network localization (SNL) in 3D was reformulated to be a nonlinear programming (NLP) problems. Feasible direction algorithm was proposed to solve the problem. The number of columns of the variables in the NLP is chosen to be equal 3, so as to avoid the higher dimensional solutions. Computational efficiency is improved by exploiting the sparsity of graph, in which the degree of each sensor node are restricted to a small positive integer. Experiments show that the proposed is efficient and robust, and the speed is faster than the existing interior-point algorithms for the SDP.
已有的无线传感器网络定位算法大多是针对平面地形的. 而在实际应用中,网络节点往往是在三维空间中. 三维无线传感器网络定位算法主要分为测距[1, 2, 3, 4, 5]和非测距算法[6, 7]. 基于接收的信号强度指示(RSSI,received signal strength indication)[1, 2, 3, 4, 5]的测距提供了最廉价的定位方法,无须额外硬件,利用对接收无线信号的强度判断,推导收发节点间的距离,所以基于RSSI的测距是无线传感器网络定位较常采用的方法.
文献[3, 4, 5]中,将满足距离条件的可行性定位问题转化为半定规划,并通过进一步松弛半定约束和利用图论知识进行稀疏,提高了计算速度. 然而,利用内点算法软件SeDuMi 1.05对半定规划进行求解影响了计算速度.
利用变量变换将半定松弛问题转换为非线性规划问题. 基于非线性规划问题具有的特殊约束条件,提出了解决非线性规划化问题的可行方向算法. 仿真实验表明,可行方向算法在计算速度上优于稀疏半定规划的内点算法.
1 半定规划模型设无向图G表示无线传感器网络,包含m个锚节点ak(k=1,2,…,m)和n个未知节点xi(i=1,2,…,n). 假设锚节点配备全球定位系统(GPS,global positioning system)装置,可测得自身位置坐标. 设2个未知节点xj和xi之间的欧式距离为dji*,测量距离为dji. 未知节点xj与锚节点ak之间的欧式距离为djk*,测量距离为djk. 在计算中只能利用测量距离来代替真实距离.
设节点的通信半径为r,取
$$\begin{gathered} {N_x} = \left\{ {\left( {{x_j},{x_i}} \right):\left\| {{x_j} - {x_i}} \right\| \leqslant r} \right\} \hfill \\ {N_a} = \left\{ {\left( {{x_j},{a_k}} \right):\left\| {{x_j} - {a_k}} \right\| \leqslant r} \right\} \hfill \\ \end{gathered} $$分别表示未知节点之间、未知节点与锚节点之间可以相连的连接节点对的集合. 为便于描述,Sn记为n阶实对称矩阵空间,Sn中的标准内积A·B =tr(ATB). $X \succcurlyeq 0$表示X是半正定矩阵. ${\mathfrak{R}^{n \times m}}$记为n×m阶实矩阵空间. ei表示第i个元素为1其余元素均为0的列向量. A(i,j),(k,h)表示由矩阵A的第i~j行、第k~h列全部元素组成的子矩阵. vec(A)表示由n×m阶矩阵A的列叠成n×m维列向量. mat(·)是vec(·)的逆运算. 0n×m记为n×m阶零矩阵.
取R=[x1,x2,…,xn]∈$\mathfrak{R}$3×n,并且
| $X = \left( {\begin{array}{*{20}{c}} {{I_3}}&R \\ {{R^{\text{T}}}}&{{R^{\text{T}}}R} \end{array}} \right)$ | (1) |
则有
| ${\left\| {{x_j} - {x_i}} \right\|^2} = {A_{ji}} 和 {\left\| {{x_j} - {a_k}} \right\|^2} = {A_{jk}}X$ | (2) |
其中
$$\begin{gathered} {A_{ji}} = \left( {0;{e_j} - {e_i}} \right){\left( {0;{e_j} - {e_i}} \right)^{\text{T}}},\forall \left( {j,i} \right) \in {N_x} \hfill \\ {A_{jk}} = \left( { - {a_k};{e_j}} \right){\left( { - {a_k};{e_j}} \right)^{\text{T}}},\forall \left( {j,k} \right) \in {N_a} \hfill \\ \end{gathered} $$利用等式(2),三维无线传感器网络定位问题可写为如下半定规划问题:
| $\begin{gathered} \min \frac{1}{2}\sum\limits_{\left( {j,i} \right) \in {N_x}} {{{\left( {{A_{ji}}X - d_{ji}^2} \right)}^2}} + \\ \frac{1}{2}\sum\limits_{\left( {j,i} \right) \in {N_a}} {{{\left( {{A_{jk}}X - d_{ji}^2} \right)}^2}} \\ \end{gathered} $ | (3) |
常等[8]利用变换X=VVT将二次半定规划转换为非线性规划,利用增广拉格朗日算法进行求解,比内点算法提高了计算效率. 利用此变换,将问题(3)转换为非线性规划. 基于问题(3)特殊的约束条件提出了可行下降方向算法.
2 非线性规划模型 2.1 非线性规划问题对任意的$X \succcurlyeq 0$,存在V∈R(n+3)×(n+3)使得X=VVT,即问题(3)的约束$X \succcurlyeq 0$等价于X=VVT,V∈R(n+3)×(n+3). 从文献[9]可知,对于三维空间内的定位问题,如果距离的测量没有误差,并且非线性规划问题(3)的解的秩为3,则公式(1)中的R就是未知结点的准确定位值. 因此取$V \in {\mathfrak{R}^{\left( {n + 3} \right) \times }}$,即V的列数选取为3,问题(3)可以写为如下非线性规划形式:
| $\begin{gathered} \min \frac{1}{2}\sum\limits_{\left( {j,i} \right) \in {N_x}} {{{\left( {{A_{ji}}V{V^{\text{T}}} - d_{ji}^2} \right)}^2} + } \\ \frac{1}{2}\sum\limits_{\left( {j,i} \right) \in {N_a}} {{{\left( {{A_{jk}}V{V^{\text{T}}} - d_{jk}^2} \right)}^2}} \\ {\text{s}}{\text{.t}}{\text{.}}\;\;{\left( {V{V^{\text{T}}}} \right)_{\left( {1:3} \right),\left( {1:3} \right)}} = {I_3},V \in {\mathfrak{R}^{\left( {3 + n} \right) \times }} \\ \end{gathered} $ | (4) |
取网络图G(V*,E),其中V*表示图的节点集,E=Nx∪Na表示图的边集. 要准确地获得未知节点的位置,需要足够的距离信息,而且每一个未知节点必须直接或间接地与锚节点相连接. 我们作如下假设:
假设1 假设网络图是连通的,而且每一个未知节点直接或间接地与锚节点相连.
在三维空间内,如果测距是准确的,对任意的一个未知节点,一般需要4个不共面的点与之相连,才能对该点进行准确的定位. 如果未知节点只和锚节点相连,由于锚节点的位置已知,很容易判断是否共面. 然而,如果未知节点和未知节点相连,仅仅根据距离不能判断与之相连的四点是否共面. 所以,不去判断四点是否共面,而是取更多的距离信息来确定未知节点的位置. 因此,对于已知的网络图G(V*,Nx∪Na),采取如下过程进行有效的稀疏[4, 5]:
1) 优先从Na中选择:如果边多于4条,选择不共面的四个锚节点对应的边,去除多余的边. 否则,选择Na中所有的边;
2)然后从Nx中选择:如果在Na中已选择4条边,去除所有Nx中的边. 否则,如果在Na中已选择k条边,则在Nx中随机选择γ-k条边. 数值实验表明,选择的边数过多并不会带来定位的更加准确,反而影响了计算的速度. 当然,选择的边数过少,会影响定位的准确性. 采用文献[4]中的取值,取γ=7.
经过上面的稀疏过程,保留了Na中对定位价值较大的边,去除多余的边. 对于Nx中的边,因为仅仅依据距离不能判断四点是否共面,所以根据需求随机选取Nx中的边.
3 可行方向算法虽然问题(4)没有了约束$X \succcurlyeq 0$,可是目标函数不再是凸函数,约束也不是线性的. 因此问题(4)是等式约束非线性规划问题,而且约束也是非线性的.
取问题(4)的可行解集为
$$F = \left\{ {V \in {\mathfrak{R}^{\left( {3 + n} \right) \times 3}}:{{\left( {V{V^{\text{T}}}} \right)}_{\left( {1:3} \right)\left( {1:3} \right)}} = {I_3}} \right\}$$下面构造可行下降搜索方向和讨论步长的确定.
3.1 构造可行下降方向按照如下步骤构造搜索方向:
1) 假设第k-1次迭代获得可行解Vk∈F,计算目标函数在Vk的梯度:
| $\begin{gathered} \nabla f\left( {{V_k}} \right) = \sum\limits_{\left( {j,i} \right) \in {N_x}} {\left( {{A_{ji}}{V_k}V_k^{\text{T}} - d_{ji}^2} \right){A_{ji}}{V_k}} + \\ \sum\limits_{\left( {j,i} \right) \in {N_a}} {\left( {{A_{jk}}{V_k}V_k^{\text{T}} - d_{jk}^2} \right){A_{jk}}{V_k}} \\ \end{gathered} $ | (5) |
2) 取${g_k} = {\text{vec}}\left( {\nabla f{{\left( {{V_k}} \right)}_{\left( {4,n + 3} \right)\left( {1,3} \right)}}} \right)$,并且令sk=vec((Vk)(4,n+3)(1,3)),利用有限存储BFGS (L-BFGS)方法[10]计算dk=Hkgk,其中Hk是正定的,取第k次迭代的搜索方向为
| ${D_k} = - \left( {\begin{array}{*{20}{c}} {{0_{3 \times 3}}} \\ {{\text{mat}}\left( {{d_k}} \right)} \end{array}} \right)$ | (6) |
下面证明构造所得的方向为可行下降方向.
定理1 若搜索方向Dk是按照上面的步骤1)和2)获得,则Dk是Vk处的可行下降方向.
证明:由步骤1)和2)可知,Hk是正定矩阵,并且
$$\begin{gathered} {\left( {{\text{vec}}\left( {\nabla f\left( {{V_k}} \right)} \right)} \right)^{\text{T}}}{\text{vec}}\left( {{D_k}} \right) = g_k^{\text{T}}\left( { - {H_k}{g_k}} \right) = \\ - g_k^{\text{T}}{H_k}{g_k} \leqslant 0 \\ \end{gathered} $$即Dk是Vk处的下降方向. 另外,设步长为αk,αk≥0,则Vk+1=Vk+αkDk,显然Vk+1∈F,即Dk是可行方向.
3.2 准确线性搜索下面讨论步长的选择,即在每一步迭代中求一元函数ϕ(α)=f(Vk+αDk),α≥0的最优解. 由于ϕ(α)是关于α的四次多项式函数,设
| $\phi \left( \alpha \right) = a{\alpha ^4} + b{\alpha ^3} + c{\alpha ^2}a\alpha + e$ | (7) |
其中
$$\begin{gathered} a = \frac{1}{2}\sum\limits_{\left( {j,i} \right) \in {N_x}} {{{\left( {p_{ji}^{\left( 2 \right)}} \right)}^2}} + \frac{1}{2}\sum\limits_{\left( {j,i} \right) \in {N_a}} {{{\left( {p_{jk}^{\left( 2 \right)}} \right)}^2}} \\ b = \sum\limits_{\left( {j,i} \right) \in {N_x}} {p_{ji}^{\left( 1 \right)}p_{ji}^{\left( 2 \right)}} + \sum\limits_{\left( {j,i} \right) \in {N_a}} {p_{jk}^{\left( 1 \right)}p_{jk}^{\left( 2 \right)}} \\ c = \sum\limits_{\left( {j,i} \right) \in {N_x}} {p_{ji}^{\left( 0 \right)}p_{ji}^{\left( 2 \right)}} + \frac{1}{2}{\left( {p_{ji}^{\left( 1 \right)}} \right)^2} + \\ \sum\limits_{\left( {j,i} \right) \in {N_a}} {p_{jk}^{\left( 0 \right)}p_{jk}^{\left( 2 \right)}} + \frac{1}{2}{\left( {p_{jk}^{\left( 1 \right)}} \right)^2} \\ d = \sum\limits_{\left( {j,i} \right) \in {N_x}} {p_{ji}^{\left( 0 \right)}p_{ji}^{\left( 0 \right)}} + \sum\limits_{\left( {j,i} \right) \in {N_a}} {p_{jk}^{\left( 0 \right)}p_{jk}^{\left( 1 \right)}} \\ e = \frac{1}{2}\sum\limits_{\left( {j,i} \right) \in {N_x}} {{{\left( {p_{ji}^{\left( 0 \right)}} \right)}^2}} + \frac{1}{2}\sum\limits_{\left( {j,i} \right) \in {N_a}} {{{\left( {p_{jk}^{\left( 0 \right)}} \right)}^2}} \\ \end{gathered} $$并且
$$\begin{gathered} p_{ji}^{\left( 0 \right)} = {A_{ji}}{H_0},p_{ji}^{\left( 1 \right)} = {A_{ji}}{H_1},p_{ji}^{\left( 2 \right)} = {A_{ji}}{H_2} \\ p_{ji}^{\left( 0 \right)} = {A_{jk}}{H_0},p_{jk}^{\left( 1 \right)} = {A_{jk}}{H_1},p_{jk}^{\left( 2 \right)} = {A_{jk}}{H_2} \\ {H_0} = {V_k}V_k^{\text{T}},{H_1} = {V_k}D_k^{\text{T}},{H_2} = {D_k}D_k^{\text{T}} \\ \end{gathered} $$因此,很容易写出多项式函数ϕ(α)的导数,进而利用一元连续函数在闭区间上的性质获得ϕ(α)在区间[0,+∞)上满足wolf条件的最优解,即满足wolf条件的最优步长. 可行方向算法的过程可以表述如下.
可行方向算法:
步骤1 第k步,已知可行点Vk-1,计算ωk=‖Δf(Vk-1)‖,若ωk满足终止条件,Vk-1即为问题的解;否则,转到步骤2;
步骤2 按照3.1,3.2节的过程计算Vk-1点处的搜索方向和步长,获得Vk=Vk-1+αk-1Dk-1,k=k+1,转到步骤1.
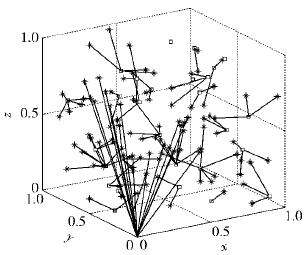
4 仿真结果及分析 4.1 可行方向算法的执行以及结果的改善因为锚节点的位置是已知的,如果未知节点与锚节点直接相连,则初始值取为离它最近的锚节点的坐标. 否则取初始值为原点坐标. 图 1体现了未知节点的初始位置,其中100个未知节点,30个锚节点,r=0.3. 其中有14个未知节点的初始位置在原点.
在可行方向算法中,取ε=10-5,当ωk<ε或者迭代次数达到200时,可行方向迭代算法终止. 将可行方向算法的结果作为初始点,利用文献[4]和[5]中采用的最速下降局部求精法改善计算结果,此方法具有全局收敛性.
4.2 数值仿真及其结果仿真是在CPU: Intel(R) Celeron(R) 2.6 GHz,内存:2 GB的个人电脑中利用Matlab 7.8进行的. 所有的锚节点和未知节点在空间区域[0, 1]3内产生,未知节点的个数为1 000个. 为了能够重复随机生成未知节点和锚节点,Matlab中的随机数取为1. 通过改变锚节点的比例、通信半径、RSSI误差系数这三类参数,观察分析它们对定位平均误差的影响,以及多参数共同作用时的影响,并进行算法相对定位误差的比较.
采用的定位平均误差为
| $\frac{1}{n}\sum\limits_{i = 1}^n {\left\| {x_i^{{\text{true}}} - x_i^{{\text{result}}}} \right\|} $ | (8) |
其中xitrue为第i个未知节点的实际位置,而xiresult是用提出的算法估计出的未知节点位置. 网络中n个未知节点的平均定位误差与通信半径r的比值记为相对定位误差.
如文献[4],用式(9)来模拟RSSI测距:
| ${\bar d_{ij}} = \left( {1 + \mu rand\left( {1,1} \right)} \right)d_{ij}^{{\text{true}}}$ | (9) |
其中:dijtrue为i,j两点间的实际距离,${\bar d_{ij}}$为所模拟的RSSI测距值,μ为RSSI测距的误差系数.
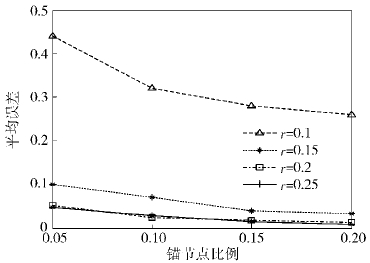
图 2表明,在不同通信半径下,随着锚节点比例增加,平均定位误差呈下降趋势. 由于当锚节点比例增加时,未知节点通信半径内的锚节点数量随之增加,未知节点可以直接获得与这些锚节点的距离信息,比通过未知节点间的距离信息进行定位更加准确. 因此,当锚节点比例增加时,平均定位误差会降低.
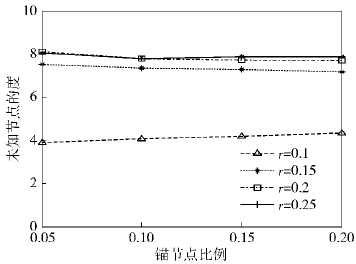
图 3体现了未知节点的度(所有节点度的平均值)随着锚节点比例和通信半径变化的变化. 随着通信半径的增加,未知节点的度也会增加. 当r=0.1时,随着锚节点比例的增加,未知节点的度会随之增加. 相反,当r>0.1时未知节点的度会减小. 因为当r=0.1时,未知节点的度均小于5,所以未知节点的度随着锚节点的增加而增加. 而当r>0.1时,未知节点的度均大于7,未知节点的度随着锚节点的增加而减少.
在图 2和图 3中,通信半径r=0.2和r=0.25的曲线图变化较小,较大的通信半径并没有带来更小的平均误差,更多的锚节点并没有提高定位误差. 这是因为采用了图的稀疏,虽然一个未知节点在较大的通信半径内有更多的锚节点和未知节点,但是稀疏之后会将一些通信半径内的未知节点去除. 而且通信半径从0.2增加到0.25后,由于对锚节点的连接数进行限制,使得通信半径内的锚节点数不会明显增多,从而导致平均误差没有多大变化.
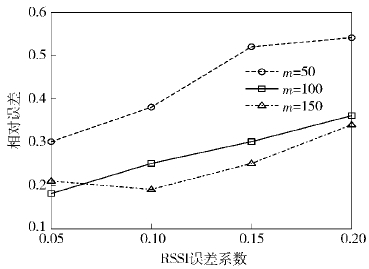
从图 4可以看出,相对误差随RSSI误差系数增加呈增加趋势,而且锚节点个数较少时,相对误差较大. 锚节点比例为15%时,相对误差介于0.2~0.3之间.
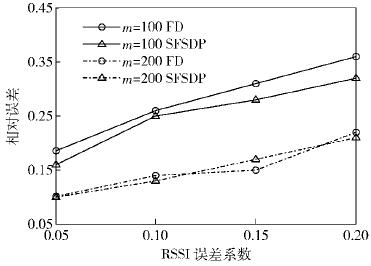
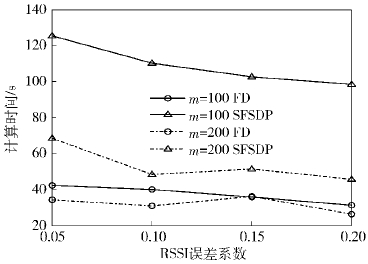
4.3 与稀疏半定规划内点算法比较在锚节点数m=100和m=200两种情况下,将提出的可行方向算法(FD,feasible direction algorithm)和文献[5]中的稀疏半定规划内点算法(SFSDP,a sparse variant of FSDP)进行比较.
从图 5和图 6可以看出,这两种算法的相对误差都随着RSSI误差系数的增加而增加,而计算时间却随着RSSI误差系数的增加有所减少. 在同等条件下,可行方向算法计算结果的准确性和稀疏半定规划内点算法基本相同. 但是,对于计算时间,可行方向算法远远优于稀疏半定规划内点算法,甚至对于m=100,μ=0.05的问题,稀疏半定规划内点算法的时间超过了120 s,而可行方向算法的计算时间不到70 s.
5 结束语
对于传感器节点数量较多的定位问题,内点算法的计算量较大,无法满足实际的需求. 为了提高计算效率,利用变量分解变换将无线传感器网络节点定位的半定规划转化为非线性规划,提出了可行方向算法. 该算法有效地提高了三维无线传感器网络节点定位的效率. 然而,随着RSSI误差系数的增加,可行方向算法定位的准确程度降低. 降低的程度对于锚节点比例较小的定位尤其明显. 因此,以后将致力于提高可行方向算法的定位准确性.
| [1] | 寿向晨, 徐宏毅. 无线传感器网络中RSSI定位算法的设计与实现[J]. 武汉大学学报:工学版, 2015, 48(2):284-288. Shou Xiangchen, Xu Hongyi. Design and implementation of RSSI localization algorithm in wireless sensor network[J]. Engineering Journal of Wuhan University, 2015, 48(2):284-288.[引用本文:2] |
| [2] | 谭志, 张卉. 无线传感器网络RSSI定位算法的研究与改进[J]. 北京邮电大学学报, 2013, 36(3):88-91. Tan Zhi, Zhang Hui. A modified mobile location algorithm based on RSSI[J]. Journal of Beijing University of Posts and Telecommunications, 2013, 36(3):88-91.[引用本文:2] |
| [3] | Biswas P, Liang T C, Wang T C, et al. Semidefinite programming based algorithms for sensor network localization[J]. ACM Transactions on Sensor Networks, 2006, 2(2):188-220.[引用本文:3] |
| [4] | Wang Z, Zheng S, Boyd S, et al. Further relaxations of the SDP approach to sensor network localization[J]. SIAM Journal on Optimization, 2008, 19(2):655-673.[引用本文:7] |
| [5] | Kim S, Kojima M, Waki H. Exploiting sparsity in SDP relaxation for sensor network localization[J]. SIAM Journal on Optimization, 2009, 20(1):192-215.[引用本文:6] |
| [6] | 孟颍辉, 闻英友, 陈剑, 等. 无线传感器网络中基于接近度的无需测距定位算法[J]. 电子学报, 2014, 42(9):1712-1717. Meng Yinghui, Wen Yingyou, Chen Jian, et al. Range free localization algorithm based on proximity fro wireless sensor network[J]. Acta Electronica Sinica, 2014, 42(9):1712-1717.[引用本文:1] |
| [7] | 蒋锐, 杨震. 基于质心迭代估计的无线传感器网络节点定位算法[J]. 物理学报, 2016, 65(3):1-8. Jiang Rui, Yang Zhen. An improved centroid localization algorithm based on iterative computation for wireless sensor network[J]. Acta Physica Sinica, 2016, 65(3):1-8.[引用本文:1] |
| [8] | 常小凯. 二次半定规划的增广拉格朗日算法[J]. 计算数学, 2014, 36(2):133-142. Chang Xiaokai. Augmented Lagrangian algorithm for solving quadratic semidefinite programming[J]. Mathematica Numerica Sinica, 2014, 36(2):133-142.[引用本文:1] |
| [9] | Man-cho So, Ye Y. The theory of semidefinite programming for sensor network localization[J]. Mathematical Programming, 2007, 109(2-3):367-384.[引用本文:1] |
| [10] | Liu D C, Nocedal J. On the limited memory BFGS method for large scale optimization[J]. Mathematical Programming, 1989, 45(1):503-528.[引用本文:1] |