2. 上海电机学院, 上海 200240
针对K用户多输入多输出干扰信道系统提出了一种基于功率分配预编码优化算法.首先通过信道的奇异值分解,基于矩阵弦距离,选出一组与最好的特征子信道最为匹配的预编码矩阵来传输信号,然后根据信道矩阵信息的强弱进行功率分配,从而对预编码矩阵进行优化,可最大化保证接收信号的强度.仿真结果表明,该算法未用迭代计算预编码矩阵和接收抑制矩阵,不仅使整个系统的复杂度大大降低,而且在系统和速率有微小损失的情况下,提高了系统的误码率性能.
The interference alignment is a transmission technology which aligns interference signal from other transmitters to the same signal subspace for reducing the interference to the desired signal. In recent years this technology has been widespread concerned. An interference alignment precoding optimization algorithm based on power allocation was proposed for the K user multiple input multiple output (MIMO) interference channel system. First, the signal is transmitted according to the best matching of the precoding matrix with the best feature sub channel based on the chord distance matrix by the singular value decomposition of the channel. Then the power allocation is assigned according to the channel matrix strength and also the precoding matrix is optimized. This method can ensure the signal strength maximally. Furthermore, the proposed algorithms calculate the precoding matrix and the receiver inhibition matrix without iteration. Simulation shows that this method not only reduces the complexity of the system, but also improves the bit error rate (BER) performance.
干扰对齐(IA,interference alignment)是一种有效的干扰管理机制,通过预编码技术使干扰在接收端重叠在一起,以彻底消除干扰对期望信号的影响[1]. 与忽略干扰、解码/消除干扰和正交接入(避免干扰)等现有处理干扰的算法不同,IA通过压缩干扰所占的信号维度,使系统获得最大自由度(DOF,degree of freedom)[2]. 由于可彻底消除干扰,能显著提高系统容量,IA技术受到广泛关注[3, 4].
Cadambe等[1]给出了一个单天线时变K用户干扰信道,可达到K/2的自由度. 为了减小干扰,王存祥等[5]给出了协作多点传输中一种基于特征子信道的干扰对齐预编码矩阵优化方案,在设计预编码矩阵时并没有充分利用系统的总功率,即在干扰子空间和期望信号映射到的子空间正交时,忽视了发射机的发送功率对接收机接收期望信号的影响. 具体来说,发射功率大小对信道信息较强的用户的影响要远小于信道信息较弱的用户,因此当信道信息较弱时,发射功率对接收期望信号的性能影响更大,即该算法在等功率分配的条件下并没有获得最优的接收性能. 在此基础上,笔者提出了一种基于功率分配的预编码优化算法,根据信道矩阵的迹的大小完成功率分配,实现预编码的优化. 仿真结果表明,在损失微小速率的情况下,系统的平均误码率性能得到了提升.
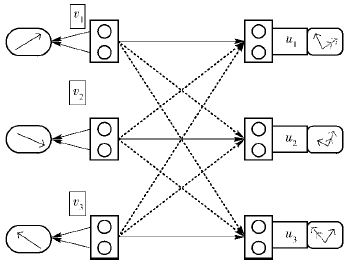
1 系统模型考虑K小区下行系统,每个小区只有1个用户,对于每个小区有多个用户的场景,可采用频分复用的方式将其简化为上述场景. 基站之间只共享信道状态信息,每个小区内的基站只给本小区用户传输数据,因而会对其他小区用户产生干扰. 同时,用户之间不进行协作. 简单但不失一般性,采用K=3的系统模型,基站和用户均配置W根天线,且W为偶数. 更为一般的场景可参考文献[1]. 系统模型如图 1所示.
小区k中用户的接收信号可表示为
| ${y_k} = {H_{kk}}{V_k}{x_k} + \sum\limits_{j \ne k} {{H_{kj}}{V_j}{x_j} + {n_k}} $ | (1) |
其中:yk为用户接收矢量;Hkj为小区j中基站到小区k中用户的信道矩阵,表征为平坦瑞利衰落,其元素服从均值为0、方差为1的独立同分布的复高斯分布;Vk为预编码矩阵;xk为小区k中基站发送的信号矢量;nk为小区k中用户的接收白噪声矢量,其分布满足nk~CN(0,σ2I). 假设每一个接收用户都知道所有的信道信息,也就是知道Hkj. 在系统中,接收用户和基站之间存在一个无干扰、无误差的广播反馈链路,基站通过接收用户反馈的有限信息获知信道状态信息.
式(1)右侧第1项为小区k中用户的有用信号,右侧第2项为多小区干扰. 因为干扰对齐要求干扰在接收端张成相同的空间,所以
| $\begin{gathered} C\left( {{H_{ik}}{V_k}} \right) = C\left( {{H_{ij}}{V_j}} \right),\forall j \ne k,\\ i \ne k,j \ne i,i,j,k = 1,2,3 \\ \end{gathered} $ | (2) |
而系统容量可表示为
| $R = \sum\limits_{i = 1}^K {{\text{lb}}} \left| {I + \frac{{{u_i}{H_{ii}}{v_i}v_i^{\text{H}}H_{ii}^{\text{H}}u_i^{\text{H}}}}{{{u_i}\left( {\sum\limits_{k \ne 1} {{H_{ik}}{v_k}v_k^{\text{H}}H_{ik}^{\text{H}} + {\sigma ^2}} } \right)u_i^{\text{H}}}}} \right|$ | (3) |
在经典干扰对齐中,式(2)中的条件简化为
| $\begin{gathered} C\left( {{H_{12}}{V_2}} \right) = C\left( {{H_{13}}{V_3}} \right) \\ {H_{21}}{V_1} = {H_{23}}{V_3} \\ {H_{31}}{V_1} = {H_{32}}{V_2} \\ \end{gathered} $ | (4) |
根据矩阵的相关理论可将式(4)变换为
| $C\left( {{V_1}} \right) = C\left( {E{V_1}} \right)$ | (5) |
| ${V_2} = {\left( {{H_{32}}} \right)^{ - 1}}{H_{31}}{V_1}$ | (6) |
| ${V_3} = {\left( {{H_{23}}} \right)^{ - 1}}{H_{21}}{V_1}$ | (7) |
| $E = {\left( {{H_{31}}} \right)^{ - 1}}{H_{32}}{\left( {{H_{12}}} \right)^{ - 1}}{H_{13}}{\left( {{H_{23}}} \right)^{ - 1}}{H_{21}}$ | (8) |
基于特征子信道的预编码优化算法不仅用到了传统算法消除其他发射机造成的干扰,而且选择信道矩阵Hii的最优特征子信道矢量构成预编码矩阵,Hii取式(8)的特征矢量集合中最为匹配发射机传输给期望接收机的信号经历的信道矩阵,从而有效地保证了接收机接收到期望信号的强度,改善了系统的可达速率性能.
首先,对本地信道矩阵Hii进行奇异值分解,将右奇异矩阵前S/2个矢量近似代替最优的特征子信道为
| $\begin{gathered} {H_{ii}} = M\Lambda {{\rm N}^{\text{H}}} \\ \left[{{m_{i1}} \cdots {m_{iS}}} \right]\left[{\begin{array}{*{20}{c}} {{a_{i1}}}&{}&{} \\ {}& \ddots &{} \\ {}&{}&{{a_{iS}}} \end{array}} \right]\left[{\begin{array}{*{20}{c}} {n_{i1}^{\text{H}}} \\ \vdots \\ {n_{iS}^{\text{H}}} \end{array}} \right] \\ \end{gathered} $ | (9) |
其中:Λ为信道矩阵Hii的奇异值按照从大到小的顺序排列构成的对角阵,对角线上的元素即为奇异值,aiS(i=1,2,3;b=1,…,S);M为左奇异向量miS(i=1,2,3;b=1,…,S)构成的矩阵;N为右奇异向量niS(i=1,2,3;b=1,…,S)构成的矩阵;niS(i=1,2,3;b=1,…,S/2)为本地信道矩阵中最优的S/2个特征子信道.
其次,计算式(9)的S个特征向量与nib的内积,并找出使内积之和最大的S/2个特征向量,这S/2个特征向量即构成优化后的预编码矩阵. 以发射机1为例,要满足以上约束条件,具体可表示为
| ${V_1} = \mathop {\arg \;\;max}\limits_{{v_{1b}} \prec {\text{eig}}\left( E \right)} \left\{ {\sum\limits_{b = 1}^{S/2} {{a_{1b}}} \left\| {{{\left( {{n_{1b}}} \right)}^{\text{H}}}{v_{1b}}} \right\|} \right\}$ | (10) |
其中:Vi为发射机1的预编码矩阵,$X \prec {\text{eig}}\left( Y \right)$表示x为Y的特征向量集合的子集,v1b为预编码矩阵Vi的第b列向量. 同时,将奇异值a1b加入内积计算,作为根据niS(i=1,2,3;b=1,…,S)选择预编码向量的影响权重因子.
最后,根据式(6)和式(7),便可计算出其他发射机的预编码矩阵V2和V3.
从上述分析可知,根据式(6)、式(7)和式(10)设计的预编码矩阵只保证了发射机1发送到接收机1的信息在最优的S/2个特征子信道中传输,并没有保证其他发射机发送的信号在对应接收机的接收强度. 类似地,如果只针对发射机2或发射机3进行上述的预编码优化算法,也不能达到整体最优的效果. 因此,为了保证整体的优化效果,需要同时设计与3条通信链路质量最好的特征子信道最为匹配的预编码矩阵. 因此可得
| $\begin{gathered} \left\langle {{V_1},{V_2},{V_3}} \right\rangle = \\ \mathop {\arg \;\max }\limits_{\begin{array}{*{20}{c}} {{v_{ib}} \prec {\text{eig}}\left( E \right)} \\ {{V_2} = {{\left( {{H_{32}}} \right)}^{ - 1}}{H_{31}}{V_1}} \\ {{V_3} = {{\left( {{H_{23}}} \right)}^{ - 1}}{H_{21}}{V_1}} \end{array}} \left\{ {\sum\limits_{i = 1}^3 {\sum\limits_{b = 1}^{S/2} {{a_{ib}}{{\left\| {{{\left( {{n_{ib}}} \right)}^{\text{H}}}{v_{ib}}} \right\|}^2}} } } \right\} \\ \end{gathered} $ | (11) |
其中:〈V1,V2,V3〉分别为3个发射机的预编码矩阵,vib为预编码矩阵Vi的第b列向量.
3 基于功率分配的预编码优化算法基于特征子信道的干扰对齐算法,在保证消除小区间干扰的前提下,尽可能地保证接收机的信号强度,但却在干扰子空间和期望信号映射到的子空间正交时,忽视了发射机的发送功率对接收机接收期望信号的影响. 具体来说,发射功率对信道信息较强的用户的影响要远小于信道信息较弱的用户,因此当信道信息较弱时,发射功率对接收期望信号的性能影响更大,即该算法在等功率分配的条件下并没有获得最优的接收性能. 针对此不足,笔者提出了基于功率分配的预编码优化算法. 因为基于特征子信道的预编码优化算法在发射机对信号进行预处理后的发射过程中,发射机分配给各接收机的功率是相同的,而在实际通信系统中,系统的接收性能与本地信道的质量直接相关,对误码率性能产生影响. 因此,上述干扰对齐算法并没有对系统的总功率进行合理的使用. 发射机采用非等功率分配问题能抽象为一个多目标优化问题,且各接收机的信道矩阵元素都是独立同分布的,因此可根据信道质量的好坏进行功率分配. 具体来说,对接收机信道质量较好的接收机分得较高的功率,对信道质量较差的接收机分得较低的功率,从整体上提高接收机接收信号的强度,降低干扰信号对期望信号的影响,从而可改善系统接收机误码率性能. 因为信道质量的好坏可根据信道矩阵特征值来判别,则它可由信道矩阵的特征值大小来表示. 所以,衡量信道质量的参数可选定为信道矩阵的迹,根据每条通信链路信道矩阵的迹来对各接收机进行功率分配. 那么,接收机K的本地信道矩阵的迹可表示为
| ${t_k} = F\left( {{H_{kk}}H_{kk}^{\text{H}}} \right)$ | (12) |
对迹的总和求平均得到
| $\bar t = \frac{1}{k}\sum\limits_{i = 1}^K {{t_i}} $ | (13) |
假设发射机的总功率为
| $P = \sum\limits_{k = 1}^K {{P_k}} $ | (14) |
那么根据信道信息的强弱对用户K进行功率分配为
| ${P_k}{\text{ = }}P\left( {\frac{{\bar t}}{{{t_k}}}} \right)/\left( {\sum\limits_{k = 1}^K {\frac{{\bar t}}{{{t_k}}}} } \right)$ | (15) |
然后对式(11)中的Vk进行归一化,将归一化后的预编码矩阵Vk与功率分配系数Pk相乘,得到优化后的预编码矩阵为
| ${\tilde V_k} = \sqrt {{P_k}} {V_k}$ | (16) |
因此,在接收机对干扰进行消除时,接收抑制矩阵需要满足
| ${\tilde U_i}{H_{ij}}{\tilde V_j} = 0,i \ne j$ | (17) |
同样地,定义一个等效信道矩阵$\tilde H_{ij}^{{\text{eff}}} = {H_{ij}}{\tilde V_j}$,对$\tilde H_{ij}^{{\text{eff}}}$作奇异值分解得到
| $\tilde H_{ij}^{{\text{eff}}} = \left[{\begin{array}{*{20}{c}} {{{\bar Q}_{ij}}}&{{{\tilde Q}_{ij}}} \end{array}} \right]\left[{\begin{array}{*{20}{c}} {\sum\limits_{ij} {} }&{} \\ {}&0 \end{array}} \right]\left[{\begin{array}{*{20}{c}} {\bar P_{ij}^{\text{H}}} \\ {\tilde P_{ij}^{\text{H}}} \end{array}} \right]$ | (18) |
根据第2节的结论可知,采用功率分配的优化算法后,得到的接收抑制矩阵为
| $\left. \begin{gathered} {\widetilde U_1} = {\widetilde Q_{12}} \hfill \\ {\widetilde U_2} = {\widetilde Q_{21}} \hfill \\ {\widetilde U_3} = {\widetilde Q_{31}} \hfill \\ \end{gathered} \right\}$ | (19) |
采用Matlab 2010b软件对以上算法进行仿真,假设基站发射功率为P=10 dBm,每个发射机的天线数为Dt=4,每个接收机的天线数为Dr=4,发射机与用户接收机之间的路径损耗为L=138.1+37.6lg(R),其中R为发射机与接收机之间实际的地理距离,单位为km. 仿真次数为1 000次. 根据式(3)计算每一个用户的速率,然后求和得到系统的和速率. 具体结果如下.
1) 当调制方式为正交相移键控(QPSK,quadrature phase shift keyin)时
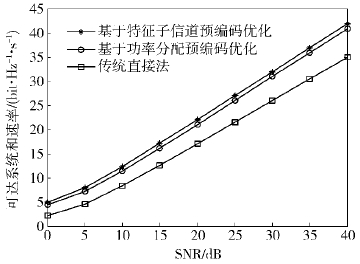
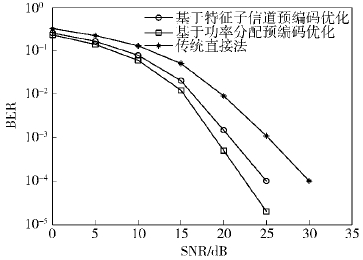
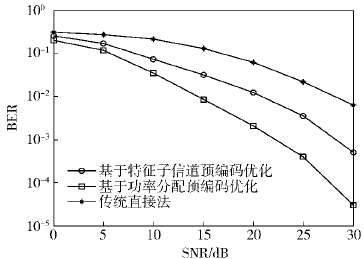
图 2和图 3给出了结合功率分配优化后的系统性能. 从图 2可以看出,基于特征子信道的预编码优化算法和基于功率分配的预编码优化算法的和速率性能都要优于传统算法,而相比于等功率分配的算法,采用功率分配对预编码进行优化后,速率有很小的降低,这是为了保证接收机接收期望信号的性能占用一定的系统资源. 从图 3可以看出,相比于基于特征子信道的预编码优化算法,采用功率分配的预编码优化算法降低了系统的平均误码率,且优于传统算法的误码率性能. 综上,验证了结合功率分配对预编码矩阵进行优化后,当速率损失在容忍范围内的情况下,能降低系统的平均误码率.
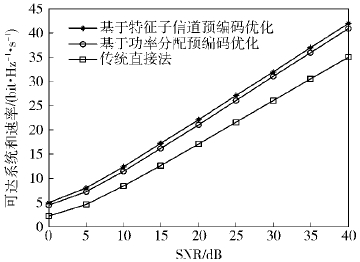
2) 当调制方式为相正交振幅调制(64QAM,64 quadrature amplitude modulation)时
从图 4可以看出,将调制方式变为64QAM后,系统的和速率并没有改变,说明调制方式对系统的和速率性能并没有影响. 从图 5可以看出,当调制方式为64QAM时,结合功率分配对预编码矩阵进行优化后,能降低系统的平均误码率. 综上,验证了采用基于功率分配的预编码优化算法后,速率虽有微小的损失,但对系统的和速率影响不大,且对误码率性能的提升效果显著.
5 结束语
主要研究了在完全信道状态下,对基于直接法设计预编码矩阵干扰对齐算法的优化. 首先针对传统干扰对齐算法主要以处理干扰信号和获取最优发送自由度为目标,忽视了发射机给期望接收机发送信号经过信道的质量问题,从增强接收机期望信号强度的角度出发,研究了基于特征子信道的预编码优化算法,通过在预编码向量集合中选择最优的预编码矩阵,使期望信号在最优的特征子信道中传输,从而提升了系统的和速率. 其次考虑该算法在设计预编码矩阵时,发射机分配给不同接收机的功率是相同的,而等功率分配并不是最优的选择,且功率因素对信道信息较弱的接收机的影响远大于信道信息较强的接收机,对此提出了基于功率分配的预编码优化算法,以信道矩阵的迹来衡量信道信息的强弱,根据信道信息的强弱来进行功率分配,从而优化预编码矩阵. 仿真结果表明,基于功率分配的预编码优化算法在系统的和速率少量损失的情况下,在误码率性能上较基于特征子信道的预编码优化算法有显著的提升.
| [1] | Cadambe V R, Jafar S A. Interference alignment and degrees of freedom of the K-user interference channel[J]. IEEE Transactions on Information Theory, 2008, 54(8):3425-3441.[引用本文:3] |
| [2] | Zheng Lizhong, Tse D N C. Diversity and multiplexing:a fundamental tradeoff in multiple-antenna channels[J]. IEEE Transactions on Information Theory, 2003, 49(5):1073-1096.[引用本文:1] |
| [3] | Sung H, Park S H, Lee K J, et al. Linear precoder designs for K-user interference channels[J]. IEEE Transactions on Wireless Communications, 2010, 9(1):291-301.[引用本文:1] |
| [4] | Nosrat-Makouei B, Andrews J G, Heath R W. MIMO interference alignment over correlated channels with imperfect CSI[J]. IEEE Transactions on Signal Processing, 2010, 59(6):2783-2794.[引用本文:1] |
| [5] | 王存祥, 邱玲. 协作多点传输中一种基于特征子信道的干扰对齐预编码矩阵优化方案[J]. 信号处理, 2011, 27(3):395-399. Wang Cunxiang, Qiu Ling. An optimized precoding scheme based on eigen-channel in interference alignment for coordinated multi-point transmission systems[J]. Signal Processing, 2011, 27(3):395-399.[引用本文:1] |