无线网络中的信息数据到达率和无线信道动态变化会使无线网络不能为用户信息的扩散提供完美的服务质量^{[1, 2]}.为了改善信息扩散的性能，网络中的节点应能对无线信道和信息数据到达率的动态变化做出及时的应对策略，从而有预见性地分配网络资源.

以无线自主网络为背景，对用户信息在动态分布式网络中的高效扩散进行研究.针对信息数据到达率和无线信道动态特性，将信息扩散描述为多用户的马尔可夫决策过程，并运用对偶分解原理将其分解.在信息数据到达率和无线信道动态变化的情况下，用户通过在线学习，仅通过1次迭代就可确定自身具有预见性的行为决策，从而达到传输收益长期最大化的目的.

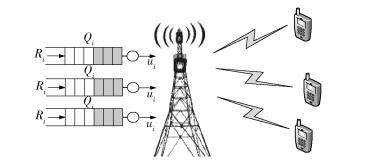
1 系统模型

考虑一个时隙离散的无线网络，如图 1所示. 无线用户用i来表示，其中1≤i≤M. 在信息扩散的过程中，若基站在时隙t为用户i分配的传输功率大小为p_i^t，则用户i的传输速率可表示为

$ u_i^t = \log \left( {1 + p_i^t{{\left| {h_i^t} \right|}^2}} \right) $

(1)

其中h_i^t为t时刻用户i的信道状态. 若基站总的传输功率为P_max，则基站为所有用户分配的传输功率需满足约束$ \sum\limits_{i = 1}^M {p_i^t < {p_{\max }}} $.

在无线网络中，各无线用户的信息数据到达率R_i^t(1≤i≤M)相互独立且服从泊松分布. 用Q_i表示基站中积压着的用户i的数据队列长度，则相邻时隙间积压的数据队列满足

$ Q_i^{t + 1} = \max \left\{ {Q_i^t - u_i^t,0} \right\} + R_i^t $

(2)

其中：R_i^t为t时刻的数据到达率，u_i^t为数据离开的速率. 假设为无线用户i分配功率p_i^t带来的收益定义为

$ \phi _i^t\left( {p_i^t} \right) = {w_i}\log \left( {p_i^t + e} \right) $

(3)

其中：w_i为无线用户i的权重，e为自然对数的底. 式(3)可表示无线用户i的公平性.

2 问题描述

李亚普诺夫稳定性理论可有效地分析网络中传输队列的稳定性.首先为基站中的用户数据队列定义一个李亚普诺夫能量函数为

$ {L^t} = \frac{1}{2}\sum\limits_{i = 1}^M {{{\left( {Q_i^t} \right)}^2}} $

(4)

定义ΔL^t=L^t+1－L^t为李亚普诺夫漂移. 根据式(2)，可得队列的李亚普诺夫漂移为

$ \Delta {L^t} \le \frac{1}{2}\sum\limits_{i = 1}^M {{{\left( {u_i^t} \right)}^2}} + \frac{1}{2}\sum\limits_{i = 1}^M {{{\left( {R_i^t} \right)}^2}} + \sum\limits_{i = 1}^M {Q_i^t\left( {R_i^t - u_i^t} \right)} $

(5)

在式(5)的左右2端加上惩罚项－VΦ_i^t(p_i^t)，其中V为正系数，得

$ \Delta {L^t} - V\sum\limits_{i = 1}^M {\phi _i^t\left( {p_i^t} \right)} \le D - \sum\limits_{i = 1}^M {\left\{ {V\phi _i^t\left( {p_i^t} \right) + Q_i^tu_i^t} \right\}} $

(6)

其中由于现实情况下的用户数据到达率和无线信道速率，常量D不可能无限大.为了保证优化过程中的队列稳定(李亚普诺夫漂移最小)，需将不等式(6)右端的项最小化^[3]. 因此，可将无线用户i的收益重新定义为

$ \bar \phi _i^t\left( {s_i^t,p_i^t} \right) = V\phi _i^t\left( {p_i^t} \right) + Q_i^tu_i^t $

(7)

其中：s_i^t=(Q_i^t,h_i^t)，则在t时刻最大化式(7)就相当于最小化李亚普诺夫漂移；s_i^t∈S_i为无线用户i在t时刻的状态，S_i为所有可能的状态集合；p_i^t∈P_i为无线用户i在t时刻的行为，P_i为所有可能的行为集合. 无线用户状态s_i^t的转移概率为

$ \begin{array}{l} \gamma \left( {s_i^{t + 1}|s_i^t,p_i^t} \right) = \\ \gamma \left( {h_i^{t + 1}|h_i^t} \right)\gamma \left( {Q_i^{t + 1}|Q_i^t,p_i^t} \right) \end{array} $

基站在t时刻观察到无线用户的状态s_i^t，为用户分配传输功率p_i^t且带来收益$ \bar \phi _i^t\left( {s_i^t,p_i^t} \right) $.在长时间内考虑无限范围的累积折扣收益，得优化问题为

$ \begin{array}{l} {U^*} = \max \sum\limits_{s_1^0 \in {S_1},\cdots ,s_M^0 \in {S_M}} {\mathop \Pi \limits_{i = 1}^M v\left( {s_i^0} \right) \times } \\ E\left[{\sum\limits_{t = 0}^\infty {\sum\limits_{i = 1}^M {{\alpha ^t}\bar \phi _i^t\left( {s_i^t,p_i^t} \right)|{s^0}} } } \right]\\ {\rm{s}}{\rm{.t}}{\rm{.}}\sum\limits_{i = 1}^M {p_i^t \le {P_{\max }}} \end{array} $

(8)

其中：s⁰={s₁⁰,s₂⁰,…,s_M⁰}为无线传输系统的初始状态，α∈(0,1)为表示瞬时优先的折扣因子，v(s_i⁰)为用户状态的初始分布. 在系统中，状态s_i的转移只依赖于行为p_i，因此该问题可描述为一个多用户的马尔可夫决策过程(MMDP，multi-user Markov decision process).

3 分布式马尔可夫决策过程 3.1 多用户的马尔可夫决策

在每一个状态s^t，对式(8)中的约束条件引入一个拉格朗日乘子λ_s^t，则式(8)的对偶函数为

$ \begin{array}{l} U\left( \lambda \right) = \mathop {\max }\limits_{p_1^0 \in {P_1},\cdots ,p_M^t \in {p_M}} \sum\limits_{s_1^0 \in {S_1},\cdots ,s_M^0 \in {S_M}} {v\left( {s_i^0} \right)} \\ E\left[{\sum\limits_{t = 0}^\infty {\alpha \sum\limits_{i = 1}^M {\left( {\bar \phi _i^t\left( {s_i^t,p_i^t} \right) - {\lambda _{st}}p_i^t + \frac{{{P_{\max }}{\lambda _{st}}}}{M}} \right)|{s^0}} } } \right] \end{array} $

(9)

原问题的对偶规划可表示为

$ {U^{\lambda ,*}} = \mathop {\min }\limits_{\lambda \ge 0} U\left( \lambda \right) $

(10)

问题为凸优化问题，所以原问题和对偶问题之间的对偶距离为0，即U^λ,*=U^*. 解决式(9)，相当于解决贝尔曼方程^[2]为

$ \begin{array}{l} U\left( {s,\lambda } \right) = \mathop {\max }\limits_{p_1^0 \in {P_1},\cdots ,p_M^t \in {p_M}} [\sum\limits_{i = 1}^M {\left( {\bar \phi _i^t\left( {s_i^t,p_i^t} \right) - {\lambda _{st}}p_i^t + \frac{{{P_{\max }}{\lambda _{st}}}}{M}} \right)} + \\ \alpha \sum\limits_{s'} {\mathop \Pi \limits_{i = 1}^M \gamma \left( {s{'_i}|{s_i},{p_i}} \right)U} \left( {s{'_i},\lambda } \right)] \end{array} $

(11)

由于资源的价格因子(即拉格朗日乘子)在各状态下不一致，所以各状态下的用户资源价格互相耦合在一起. 因此，暂时先假设1个各状态一致的价格因子，则式(9)可表示为

$ \begin{array}{l} U\left( \lambda \right) = \mathop {\max }\limits_{p_1^0 \in {P_1},\cdots ,p_M^t \in {p_M}} \sum\limits_{s_1^0 \in {S_1},\cdots ,s_M^0 \in {S_M}} {v\left( {s_i^0} \right)} \times \\ E\left[{\sum\limits_{t = 0}^\infty {{\alpha ^t}\sum\limits_{i = 1}^M {\left( {\bar \phi _i^t\left( {s_i^t,p_i^t} \right) - {\lambda _{st}}p_i^t + \frac{{{P_{\max }}{\lambda _{st}}}}{M}} \right)|{s^0}} } } \right] \end{array} $

(12)

对应的对偶规划为

$ {{\hat U}^{\lambda ,*}} = \mathop {\min }\limits_{\lambda \ge 0} U\left( \lambda \right) $

(13)

由于一致的价格因子，对偶规划式(13)不再和原问题存在强对偶关系. 相反，和它强对偶的问题为

$ \begin{array}{l} {{\hat U}^*} = \max \sum\limits_{s_1^0 \in {S_1},\cdots ,s_M^0 \in {S_M}} {\mathop \Pi \limits_{i = 1}^M v\left( {s_i^0} \right) \times } \\ E\left[{\sum\limits_{t = 0}^\infty {\sum\limits_{i = 1}^M {{\alpha ^t}\bar \phi _i^t\left( {s_i^t,p_i^t} \right)|{s^0}} } } \right]\\ {\rm{s}}{\rm{.t}}{\rm{.}}\sum\limits_{t = 0}^\infty {\sum\limits_{i = 1}^M {\left( {{\alpha ^t}} \right)\left( {p_i^t - \frac{{{P_{\max }}}}{M}} \right)} \le 0} \end{array} $

(14)

进一步发现，式(14)和式(8)中的约束满足的关系为

$ \left\{ {\sum\limits_{i = 1}^M {p_i^t \le P\max } } \right\} \subset \left\{ {\sum\limits_{t = 0}^\infty {\sum\limits_{i = 1}^M {\left( {p_i^t - \frac{{{P_{\max }}}}{M}} \right)} \le 0} } \right\} $

即式(8)中的约束为式(14)中约束的子集，因此有

$ {{\hat U}^{\lambda ,*}} = {{\hat U}^*} \ge {U^{\lambda ,*}} = {U^*} $

(15)

从中可以看出，$ {{\hat U}^*} $为原问题的上界.

按文献[2]给出的策略，在设置各状态一致价格因子的情况下，式(14)的贝尔曼方程可分解为M个局部的贝尔曼方程和1个资源价格更新方程，且每一个局部的贝尔曼方程可描述为1个局部的马尔可夫决策过程(MDP，Markov decision process)，即问题式(14)的贝尔曼方程可表示为

$ U\left( \lambda \right) = \sum\limits_{i = 1}^M {\sum\limits_{s_0^i} {v\left( {s_0^i} \right){U^i}\left( {s_0^i,\lambda } \right)} } $

(16)

其中

$ \begin{array}{l} {U^i}\left( {s_0^i,\lambda } \right) = \mathop {\max }\limits_{{p_i} \in {P_i}} {{\bar \phi }_i}\left( {{s_i},{p_i}} \right) - \lambda {p_i} + \frac{{{P_{\max }}}}{M} + \\ \alpha \sum\limits_{s'} {\gamma \left( {{s_i}'|{s_i},{p_i}} \right)U\left( {{s_i}',\lambda } \right)} \end{array} $

(17)

对于资源价格，则按更新策略更新为

$ {\lambda ^{k + 1}} = {[{\lambda ^k} + {\beta ^k}\left( {\sum\limits_{i = 1}^M {{Z^i} - \frac{{{P_{\max }}}}{{1 - \alpha }}} } \right)]^ + } $

(18)

其中：$ {Z^i} = {\sum\limits_s {v\left( s \right){e^T}\left( {I - \alpha \Gamma } \right)} ^{ - 1}}p $为折扣累积资源开销的期望，Γ为状态转移矩阵，p为资源分配向量；β为步长因子，满足

$ \sum\limits_k {{\beta ^k} = \infty } ,\sum\limits_k {{{\left( {{\beta ^k}} \right)}^2} < \infty } $

在前面的讨论中，式(12)强制使用了1个各状态一致的价格因子，且得出算法性能的上界$ {{\hat U}^*}\left( {{{\hat U}^*} \ge {U^*}} \right) $. 然而，此解有可能违反原问题中的功率约束而变得不可行.为了避免违反原问题中的功率约束，即$ \sum\limits_{i = 1}^M {p_i^t} > {P_{\max }} $，使用收缩规则对分布式MDP得到的最优解{p_i^*|i=1,…,M}处理为

$ \hat p_i^* = \frac{{p_i^*}}{{\sum\limits_{i = 1}^M {p_i^*} }}{P_{\max }} $

(19)

经收缩后的解为资源分配机制的解.

3.2 基于模型的学习策略

将无线用户在状态s_i下采取行为p_i的值函数定义为

$ \begin{array}{l} {G_i}\left( {{s_i},{p_i}} \right) = {{\bar \phi }_i}\left( {{s_i},{p_i}} \right) - \lambda {p_i} + \frac{{{P_{\max }}}}{M} + \\ \alpha \sum\limits_{s'} {\gamma \left( {{s_i}'|{s_i},{p_i}} \right)U\left( {{s_i}',\lambda } \right)} \end{array} $

(20)

在自主学习的框架中，通过值函数G_i(s_i,p_i)来确定资源的分配策略. 由于各无线用户的学习过程基本相同，在下面的描述中省略状态和行为的下标. 在值函数更新的过程中，需要知晓用户节点的状态转移概率，但在现实情况下，状态转移概率并不能提前得知，因此需要在资源的分配过程中，对用户状态随行为变化的规律进行学习，并对状态转移概率进行估计. T_s,s′^t(p)为无线用户状态转移概率的估计值，并在值函数的更新过程中随时间不断更新.在基于模型的学习策略中，采用最大似然策略来估计无线用户的状态转移概率. n_s,s′^t(p)为截止服务时刻t，无线用户在状态s时选择行为p并使状态从s转移到s′的次数. N_s^t(p)为截止服务时刻t，无线用户在状态s时选择行为p的次数. 对节点的状态转移概率估计为

$ T_{s,s'}^t\left( p \right) = \frac{{n_{s,s'}^t\left( p \right)}}{{N_s^t\left( p \right)}} $

(21)

其中T_s,s′^t(p)为状态转移概率的估计值，根据长期的观察统计得到，并在每个时刻进行更新.无线用户在每个时隙根据值函数做出资源分配策略. 在初始时刻，假设所有的值函数为0，即$ G\left( {s,p} \right) = 0,\forall s,p $. 无线用户在选择行为p作为资源分配策略后对下一时刻的G(s,p)值进行更新.

$ \begin{array}{l} {G^{t + 1}}\left( {s,{p^t}} \right) = \left( {1 - {p^t}} \right){G^t}\left( {s,{p^t}} \right) + {p^t}\{ {{\bar \phi }_i}\left( {{s_i},{p_i}} \right) - \\ \lambda {p_i} + \frac{{{P_{\max }}}}{M} + \alpha \mathop {\max }\limits_P \sum\limits_{s'} {{T_{s,s'}}\left( p \right){G^y}\left( {{s^{t + 1}},p} \right)\} } \end{array} $

(22)

其中0<ρ<1为学习速率，为了保证G(s,p)值的收敛性，要求$ \sum\limits_t {{p^t} = \infty } ,\sum\limits_t {{{\left( {{p^t}} \right)}^2} < \infty } $. 当无线用户处于状态s时，使用软平稳策略来选择行为，Ω(s,p)为用户在状态s时选择行为p的概率，软策略通过波尔兹曼分布定义为

$ \Omega (s,p) = \frac{{{\rm{exp}}\left( { - {G^t}\left( {s,p} \right)/\tau } \right)}}{{\sum\limits_{p'} {{\rm{exp}}\left( { - {G^t}\left( {s,p} \right)/\tau } \right)} }} $

(23)

其中τ为调节参数，参数τ较小时，在相同的状态下，不同的行为被选择的概率相差比较大.在每个服务间隔内，用户需要对每一个状态的G(s,p)值进行更新. 完成G(s,p)值的更新后，再通过式(23)确定策略.

4 仿真分析

采用Matlab软件对用户信息在自主无线网络中的扩散问题进行仿真，并与文献^[4]中的Q学习策略进行比较. 需要指出的是，文献^[4]中的Q学习策略没有对式(22)中的状态转移概率进行学习. 设α=0.75，ρ=0.5.

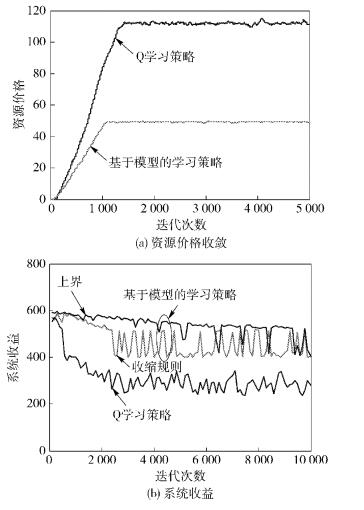
图 2(a)示出了基于模型学习策略和Q学习策略的资源价格收敛曲线. 可以看出，基于模型的学习策略可获得比Q学习策略更低的资源价格和更快的收敛速率. 这是因为在基于模型的学习策略中，用户可根据状态转移概率的估计值作出更准确的预见性决策，因此可获得更低的资源价格和更快的收敛速度.

图 2(b)示出了2种学习策略下系统的长期收益.可以看出，基于模型的学习策略能获得更高的长期收益，这是因为在基于模型的学习策略中，有着更低的资源价格，所以用户可获得更多的资源来提升系统的长期收益.图 2中系统性能的上限表示不使用收缩规则时系统的长期收益，由式(15)给出.可以看出，在收缩规则下，系统的长期收益近似达到上限.

表 1所示为累积折扣因子对系统收益和系统达到稳定所需迭代次数的影响.可以看出，α越大，系统收益越高，但达到稳定所需的迭代次数越多.这是因为α越大，系统越多考虑将来时刻收益，从而产生更高的系统收益和花费更长的时间进行学习.

表 2分析了学习速率ρ对系统性能的影响.从表 2可以发现，ρ越大，系统收益越低.这是因为ρ越大，系统越忽略过去的经验值(见式(22))，从而造成较低的系统收益. 从表 2还可以看出，当0.5<ρ<0.7时，系统有较好的收益和收敛速率.

5 结束语

针对无线自主网络中的信息扩散问题，提出了一种自主的资源分配策略，并使用李亚普诺夫漂移的方法来分析网络的稳定性.随后，将问题描述为一个多用户的马尔可夫决策问题，并提出了一种对偶分解方法将问题进行分解.对于未知的信息数据到达率和无线信道状态，用户通过在线学习可确定自身具有预见性的行为决策，且能使长期传输收益最大化.