电子侦察是信息的重要来源，在现代复杂的雷达对抗信号环境中，如何快速准确地对雷达信号进行正确地分选和匹配显得尤为重要^[1].目前传统的雷达侦察主要是依靠信号在时间、空间、频谱等特征参数的差别进行分选和辐射源检测^{[2, 3, 4]}.基于脉冲重复周期的信号分选方法，聚类分选方法，多参数模板匹配方法以及基于脉内调制的分选方法均是基于信号参数级进行分选，但对于大量在时间、空间、频谱上的随机交叠信号，现有的许多参数测量方法无法进行有效的分辨，造成测量和检测错误，进而影响分选的正确率. 笔者基于压缩感知理论，将待分选信号在过完备样本字典下进行稀疏表示，提出了一种新的雷达信号分选方法，以少量的观测数据，就可以实现对随机交叠雷达信号的快速分选.

1 压缩感知理论

压缩感知是基于信号稀疏性的采样理论^[5]，其主要思想是：如果信号在某个变换域是稀疏的或可压缩的，就可以利用一个与变换基不相关的观测矩阵将信号投影到一个低维空间上，利用少量的观测值，通过求解一个最优化的问题恢复出原信号. 设长度为N的信号x在一组基Ψ=[Ψ₁,Ψ₂,…,Ψ_N]，(Ψ_i为N维列向量)下的系数为α=[α₁,α₂,…,α_N]，即

$ x = \sum\limits_{i = 1}^N {{\psi _i}{\alpha _i}} $

(1)

写成矩阵形式为

$ x = \Psi {\alpha ^{\rm{T}}} $

(2)

其中：Ψ为N×N矩阵，α为1×N维向量. 若向量α中只有$ {\rm{k}} \ll N $个非零系数时，则称信号是稀疏(可压缩)的，称Ψ为信号x的一个基.

压缩感知观测模型中，利用一个M×N维的观测矩阵Φ对信号x进行压缩采样，得到M×1维观测向量y($ {\rm{k < M}} \ll N $)：

$ y = \Phi x = \Phi \Psi {\alpha ^{\rm{T}}} = \Theta {\alpha ^{\rm{T}}} $

(3)

其中Θ=ΦΨ，为M×N维矩阵恢复矩阵.

由于观测向量y的维数M远小于信号的长度N，且M个观测值已经包含了信号的全部信息，M的取值与观测矩阵的结构和信号的稀疏表示均有关系，压缩感知理论指出，观测矩阵Φ要满足等距约束性准则^[6]，而高斯随机测量矩阵具有很好的等距约束常数，信号能够以很高的概率实现重构.

2 基于压缩感知的雷达信号分选算法

现代雷达对抗信号环境密度大，范围广，为满足实时性的要求，侦察过程中必须在最短的时间内利用最少量的数据来完成雷达信号的比对与分选.侦察接收机收到的是辐射源直接发射的信号，信号能量反比于距离的二次方，具有距离优势，所以在许多情况下(如主瓣侦收)可以获得高信噪比辐射源的原始信号样本，而威胁雷达信号往往会多次出现，这就可以利用辐射源信号的重复性和截获的信号样本进行快速的雷达信号分选.

2.1 待分选雷达信号的稀疏表示

雷达信号分选的实质就是找出信号之间在某一维特征空间上的不同，进而将其分离开，而提取出的各维特征参数就是信号所包含的信息，因此完全可以直接利用信号所包含的信息的不同将其分选出来.利用压缩感知模型将待分选的雷达信号进行稀疏表示，经过压缩采样大大降低了数据的处理量.不但对于常见的雷达信号形式(单载频、线性调频、二相编码等)能很好地分选，并且可以对时域交叠，频域交叠等利用传统方法很难区别的信号进行很好的分离.

假设待分选的雷达信号为x(t)，已知的雷达信号样本记为Ψi(N×1维向量)，表示的是第i个归一化雷达原始信号样本.由于考虑到雷达信号的多样性，很难用一个正交基稀疏表示各种形式的信号. Peyre指出利用冗余字典代替正交基可以得到信号更为稀疏的表示[7]，而Rauhut等[8]则证明了信号在冗余字典下进行稀疏表示，仍可利用压缩感知重构算法实现信号的重构或近似重构. 由于信号的稀疏性是压缩感知理论的先决条件，所以首先要能对待分选的雷达信号进行很好的稀疏表示. 雷达原始信号样本{Ψi}Nsi=1是利用先验信息和实际侦收的雷达信号产生的，而待分选的雷达信号是其一个极小子集，所以待分选信号在雷达原始信号样本空间上具有良好的稀疏性. 利用{Ψi}Nsi=1建立过完备稀疏字典Ψ

$ \Psi {\rm{ = }}\left[{{\psi _1},{\psi _2},\ldots {\psi _{{N_s} - 1}}} \right] $

(4)

其中：过完备稀疏字典Ψ为N×N_s维矩阵，Ψ_i为第i个归一化雷达原始信号样本，N_s为字典的长度，则待分选的雷达信号x(t)可以表示为

$ x\left( t \right) = \sum\limits_{i = 1}^k {{\alpha _i}{\psi _i}\left( t \right) + \varepsilon \left( t \right),{\alpha _i} \ne 0} $

(5)

其中：k为待分选雷达信号中所包含的信号个数，Ψ_i是字典中的第i列，称为字典中的一个原子，α_i为相应原子对应的系数，ε(t)为多普勒频差、迟延等因素的误差分量. 待分选的雷达信号x(t)在Ψ上稀疏表示后，得到稀疏系数构成的稀疏向量α=[α₀,α₁,…,α_Ns－1]^T，写成矩阵形式如式(6)所示.

$ x\left( t \right) = \Psi \alpha + \varepsilon \left( t \right) $

(6)

信号在稀疏字典上的稀疏度就是待分选雷达信号中所包含的信号个数k，稀疏向量α中的每一个系数α_i的值代表了信号对应的幅度，而α_i的所在稀疏向量中α的位置则对应了字典相匹配的原子.因此，基于雷达信号原始样本建立的过完备稀疏字典不但能够对待分选的雷达信号进行稀疏表示，还能够对其进行有效的分选.

考虑到实际应用中待分选信号和样本信号噪声的影响，待分选的雷达信号x(t)可以表示为

$ x\left( t \right) = \Psi \alpha + \varepsilon \left( t \right) + n\left( t \right) = \Psi \alpha + w\left( t \right) $

(7)

其中w(t)为各种因素引入的误差.在雷达信号的原始样本空间构建的过完备稀疏字典中，若待分选的雷达信号与字典中某一个或某几个原子(某个或某些独立的雷达信号样本)高度匹配，则相应的系数α_k为远大于零的值，而其他原子上的系数近似为零.由于待分选的雷达信号x只包含了过完备稀疏字典中的k个分量，则信号的稀疏度为k，远小于信号的实际长度N，因此，信号的采样率不再取决于带宽，而是取决于信号在字典下的稀疏程度.

2.2 压缩采样求解

为了实现对待分选的雷达信号x(t)进行压缩采样，得到压缩后的观测数据y，y与矩阵Θ={θ_m,n}和稀疏系数α之间的关系为

$ y = \Theta \alpha = \Phi \Psi = \Phi x\left( t \right) + w\left( t \right) $

(8)

其中：y为M×1维向量，Φ为M×N的高斯随机观测矩阵，Θ为M×N_s矩阵，w(t)为噪声.

由于压缩采样后测量值y的维数为M维，远小于信号的长度，所以大大降低了A/D的采样速率和数据处理量，只需知道稀疏向量α中非零系数的位置，就实现了雷达信号的分选.式(8)中稀疏系数α的求解可以转化成如下优化问题：

$ \mathop {\min }\limits_\alpha {\left\| \alpha \right\|_1}{\rm{s}}{\rm{.t}}{\rm{.}}\;{\left\| {\Theta \alpha - y} \right\|_2} < \varepsilon $

(9)

其中ε为误差量. 利用压缩感知重构算法可以求取最优解，得到稀疏向量α. α中峰值α_k的位置即表示信号与过完备稀疏字典中的原子Ψ_i相匹配. 若同时在α中多个位置出现峰值，则证明当前信号是过完备稀疏字典中多个原子的线性叠加；若信号在α中无峰值出现，则可认为此信号为收集到的新样本，将其补充到过完备稀疏字典中，以便于进行下次侦收. 侦收一段时间后，根据信号与字典中各原子的匹配程度和出现次数等，选取特定威胁等级的信号进行有针对性的后续信号处理.

3 算法分析

传统的分选算法是在对信号进行检测和参数测量，然后基于提取出的多维信号参数来对信号进行分选. 即传统的分选算法是参数级的信号分选，提取的是有限维信号参数，当信号在这些维参数上相同时则无法有效的分选，而提取的参数维数又不能无限多，这也是参数级分选算法的局限性. 另一方面，参数级信号分选算法是建立在Nyquist采样定理的基础上的，实现的前提是能够对信号进行完整的取样并且准确地获取信号参数.本文所提出的算法则是利用信号之间的相关性直接在信号级进行分选，且能够在对信号压缩采样的条件下实现信号的分选，取得较好的分选效果.与传统的分选算法相比，该算法利用的是压缩采样后得到的M维观测数据进行运算，且M维观测值已经包含了信号的全部信息，所以极大地降低了A/D的采样速率和后续的数字信号处理的数据量，而且算法的分选过程是在信号级进行的，省去了传统算法中信号参数提取的过程，只利用较少的压缩采样值完成信号的分选，过程更为简单.

由于待分选的雷达信号观测时初相位存在着一定的差异，而利用过完备稀疏字典对信号进行分选利用的是信号与字典中原子的匹配程度(或信号之间相关性的强弱)，若同一信号之间的相位差过大，则信号之间的相关性会明显减弱，甚至失配，造成检测错误.为了使得构建的过完备稀疏字典对于信号的初相位具有一定的鲁棒性，可以利用相位量化的方式予以解决，相位量化后的字典表示为

$ \Psi = \left[{{{\bar \psi }_1},{{\bar \psi }_2},\cdots {{\bar \psi }_{{N_s} - 1}},} \right] $

(10)

其中

$ \begin{array}{l} {{\bar \psi }_i} = \left[{{\psi _i}{e^{j\varphi 0}},{\psi _i}{e^{j\varphi 1}},\cdots {\psi _i}{e^{j\varphi L - 1}}} \right],\\ \;\;\;\;\;\;\;\;\;\;\;i = 0,1,\cdots ,{N_s} - 1 \end{array} $

(11)

φ_k=2kπ/L,L为相位量化位数，k=0,1,…,L－1. 字典的长度也由N_s维变成了N_sL维，若L选得过大会使的字典的长度急剧增加，造成雷达原始信号样本的冗余，且破坏了样本之间的独立性，故只选φ₀=0，φ₁=π/2两个正交的相位就可以对信号进行很好的区分,此时相当于将信号在过完备稀疏字典上的投影值进行正交分解，由正交性可知，信号能量保持不变.

由于信号在传播过程中不可避免地会产生到达时间的迟延和多普勒频差，使得待分选的雷达信号不能够完全表示为样本信号的线性组合，会引入一定的误差分量，如式(5)所示.由于雷达信号样本存储的均是雷达信号脉内波形，待分选的雷达信号采样的也是脉冲持续期间的数据，所以不会由于到达时间不同而出现失配；而由于时间同步问题，由采样间隔引起的迟延是存在的，但是这个迟延通常较小，待分选信号与样本信号之间仍有较强的相关性，一般不会产生失配.算法对待分选的射频信号直接进行压缩采样，字典中存储也是射频信号的原始样本，因此，多普勒频差与载频相比相差了几个数量级，一般不会影响信号之间的匹配，所以也对分选结果影响较小.

4 仿真结果

为了验证所提分选算法的正确性与有效性，进行如下仿真实验.仿真中选取常见的雷达信号形式，且特征参数互有交叠.

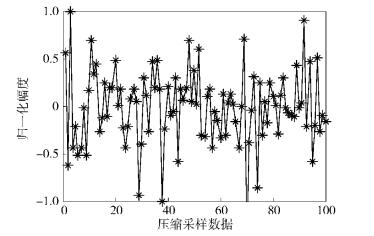
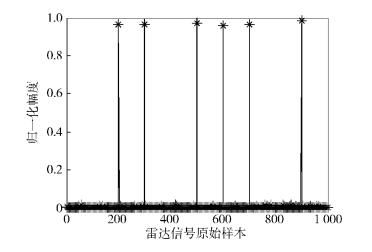
仿真1 假设待分选的雷达信号长度N=500，由6个时频交叠的雷达信号混合而成，SNR为20 dB. 3个单载频信号频率分别为10、20和30 MHz；2个线性调频信号，中心频率分别为30 MHz和40 MHz，带宽分别为40 MHz和20 MHz；1个相位编码信号，载频20 MHz，采用巴克码方式编码. 构建的过完备稀疏字典的长度N_s=1 000，存有雷达信号的原始样本，并假设待分选的雷达信号均在字典中.采用高斯随机矩阵对其进行压缩采样，采样次数M=100，得到的时域波形如图 1所示，利用压缩后的少量观测数据进行分选，得到分选结果如图 2所示.

从图 1可以看出，由于进行了压缩采样，极大地降低了采样率，虽然只获得了100个观测数据，但是这100个观测值已经包含了信号的全部信息.由于选取的待分选信号在时域上交叠，且信号在频域上也有重叠，利用传统的参数测量的分选方法很难区分开来，而利用信号在过完备稀疏字典上的稀疏性，通过寻找稀疏系数的位置，就可以得到良好的分选结果.如图 2所示，待分选信号分别于字典中的第200、300、500、600、700和900个原子相匹配，则证明了信号中包含了这几个分量，再根据字典中相应原子已知的信息，很容易获取信号的特征，对于多次出现的威胁信号则可进行后续处理，以得到更为细致的特征参数.

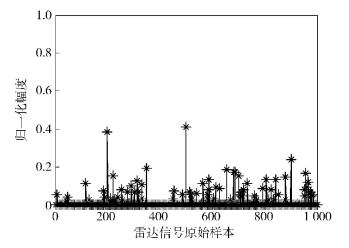
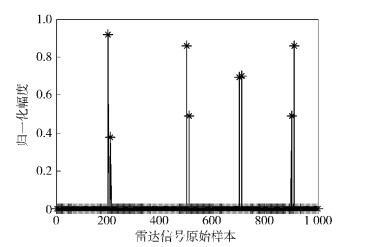
仿真2 根据前面的分析，待分选雷达信号的初相位不同也会对分选结果造成影响，为了使分选算法对于信号的初相具有一定的鲁棒性，可以运用相位量化的方法，每个雷达信号样本选取初相为0和π/2两个正交相位构建过完备稀疏字典，再进行分选.选取初相位分别为π/8、π/6、π/4、π/3的4个单载频信号，图 3、图 4分别给出了未经相位量化和相位量化后的分选结果.

从图 3中可见，由于未对相位进行量化，而待分选的雷达信号附加了不同的初相位，造成了与字典中原子的失配，难以找到匹配的分量，导致分选失败.而相位量化后，待分选的雷达信号在两个正交的样本上均有投影分量，相当于将信号的投影值进行了正交分解，信号的总能量等于两正交分量的矢量合成，并且通过两个正交分量上投影值的大小，还可以近似计算出待分选雷达信号中每个信号的初相位(见图 4).

$ {\varphi _0}{\rm{ = arctan}}\left( {\frac{{{P_{\pi /2}}}}{{{P_0}}}} \right) $

(12)

其中：P₀为0相位样本上的投影值，P_π/2为π/2相位样本上的投影值.

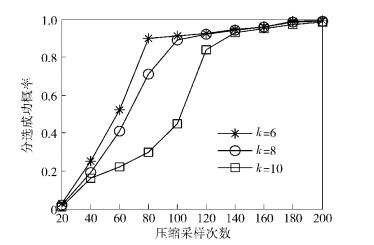
仿真3 压缩采样的次数直接影响了A/D的采样速率和数据处理量的大小，也是影响算法快慢和复杂度的重要因素，而压缩采样的次数与待分选的雷达信号长度和信号在字典下的稀疏度均有关系.从稀疏字典中随机选取雷达信号组成待分选的雷达信号进行验证，信号长度N=500，每个压缩采样值下分别进行1 000次蒙特卡罗实验，得到分选成功概率(全部信号均分选出来才算成功)与压缩采样观测次数之间的关系曲线，如图 5示.

如图 5所示，三条曲线分别给出了信号稀疏度k=6,8,10(待分选雷达信号中包含的信号个数)时的分选成功概率与压缩采样观测次数之间的关系.当待分选的雷达信号长度一定时，包含的信号个数越多，对应的信号稀疏度越大，则需要压缩采样的次数也就越多. 压缩采样次数M一般要满足M≥cklg(N/k)，其中c是常数，不同的观测矩阵、稀疏字典的构建以及不同的重构算法M的取值一般也会有所不同，在随机高斯观测矩阵的情况下，采用基追踪算法，压缩采样次数M近似满足M≈2klg (N)，这时可以保证信号能够以很高的概率分选成功.

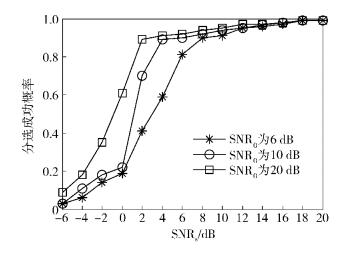
仿真4 实际的雷达信号中均会有噪声的存在，而信噪比则会对信号分选的性能产生重要的影响. 算法中信噪比的影响包括两部分，即雷达信号原始样本的信噪比SNR₀和待分选的雷达信号的信噪比SNR_s.每个信噪比下随机选取6个雷达信号组成待分选的雷达信号进行验证(假设选取的信号均在字典中有对应的雷达信号原始样本)，分别进行1 000次蒙特卡罗实验，记录分选成功次数(全部信号均分选出来才算成功). 图 6所示为不同信噪比下的分选成功概率，在雷达信号原始样本信噪比SNR₀分别等于6、10和20 dB的条件下得到的待分选雷达信号的信噪比SNR_s与分选成功概率之间的关系.从仿真结果可以看出，提高待分选雷达信号的输入信噪比和样本信噪比均有利于分选成功概率的提高，其中样本的信噪比对于分选成功的概率至关重要，若具有高信噪比的雷达信号原始样本，就可以实现在低信噪比的情况下对信号进行分选，成功概率仍然很高. 而实际情况中，由于电子侦察接收机具有距离优势，接收的是辐射源直接发射的信号，所以往往可以截获到高信噪比的信号样本，使得该分选算法在低信噪比下仍能达到较为理想的效果.

5 结束语

压缩感知理论是一种不同于传统的Nyquist采样定理的信息采样理论，在该理论下信号的采样速率不再取决于信号的带宽，而是取决于信号中所包含的信息.笔者结合电子侦察中的雷达信号分选问题，提出了一种能快速进行雷达信号分选的新算法，将信号的分选问题转化成了在压缩采样的情况下，求解稀疏系数的问题，大大减少了数据处理量，并且对于大量的信号在时间、空间、频谱发生随机交叠，低信噪比等情况下均能取得较理想的分选效果.