为了提高大规模天线能量广播系统的平均用户能量收获效用,在采用最大比传输预编码下,利用大规模天线的性质推导了单能量源场景的最优功率分配方案,利用小区间干扰提出了多能量源协作传输方法,并给出了协作能量传输的最优功率分配方案.仿真结果表明,在单能量源中,所提功率分配方案的性能好于等功率分配方案的性能,协作能量传输方案的性能优于非协作能量传输方案的性能.
In order to improve the average user utility of energy harvesting in energy broadcasting system with massive antennas, the maximum ratio transmission precoder was employed. Considering the single energy source scenario, the optimal power allocation scheme is first derived with aid of advantage of the characteristics of massive antennas. To exploit the inter-cell interference, a cooperative energy transfer scheme was proposed in multiple energy sources scenario, and the optimal power allocation for cooperative energy transfer was deduced correspondingly. Simulations indicate that the performance with the optimal power allocation is better than that with equal power allocation in single energy source scenario, and the cooperative energy transfer outperforms the non-cooperative energy transfer in multiple energy sources scenario.
无线能量传输被视为解决真正“无线”通信的重要技术[1]. 其研究内容主要包括射频长距离无线能量传输和电磁耦合近场能量传输技术等[2]. 在单用户能量传输系统中,无线信息与能量混合传输的时分和功分方案已经成为学术界的研究热点[3]. 而考虑到大规模天线可利用极窄波束成倍提高多用户的信号接收强度,布置大规模阵列的系统不仅可改善系统的谱效和能效,而且可增强无线能量传输的效率[4],因此笔者研究大规模天线系统中的能量广播技术.
为了提高大规模天线系统能量广播的平均用户能量收获效用,笔者采用最优能量广播的最大比传输预编码[5],首先在单能量源下,利用大规模天线的性质推导了系统的最优功率分配,并与等功率分配方案进行对比. 其次考虑到小区间干扰有益于用户的能量收获,提出了多能量源协作能量传输方案,推导了该方案下的最优功率分配,并与非协作能量传输方案进行对比.
1 能量广播系统模型如图 1所示,考虑一个下行能量广播系统、一个M根天线的能量站同时同频服务K个单天线能量请求用户,且M $ \gg $K.系统采用时分复用模式,用户在上行传输正交导频序列,基站根据接收到的导频信号可估计得到上行信道,进而根据信道互易性得到下行信道. 基站利用得到的下行信道构造预编码,在TE时间内给用户广播能量.
假设gk=θk1/2hk∈CM(k=1,2,…,K)为从用户k到能量站的信道向量,其中θk为包含路径损失和阴影衰落的大尺度衰落系数,hk=[hk1,hk2,…,hkM]T为小尺度衰落向量,且其元素hkm为标准复高斯随机变量,即hkm~CN(0,1).
首先,在大规模天线系统中,最大比传输预编码对能量传输是最优的[5, 6];其次,能量请求用户仅在射频处收获能量,而不进行基带的解调解码等,因此能量站可给不同能量用户传输相同的符号s,且满足|s|=1. 因此,多用户的能量传输预编码为
| $ w(\alpha ) = \sum\limits_{k = 1}^K {{\alpha _k}{g_k}^*} $ | (1) |
其中α=[α1,α2,…,αK]T为包含预编码组合系数的向量,且满足归一化条件$ {\left\| {w(\alpha )} \right\|^2} = 1 $.
当能量站的总传输功率为p/M时,其传输信号为$ \sqrt {p/M} w\left( \alpha \right)s $. 进而第k个用户接收到的信号为
| $ {y_k}\left( \alpha \right) = \sqrt {p/Mg} _k^Tw\left( \alpha \right)s + {n_k} $ | (2) |
其中噪声nk~CN(0,σ2). 假设能量收获效率为η,则用户k在时间TE内收获的能量为
| $ \begin{array}{l} {E_k}\left( \alpha \right) = \eta {T_E}E[|{y_k}\left( \alpha \right){|^2}] = \\ \eta T\left\{ {\frac{p}{M}E[{\rm{|}}g_k^Tw\left( \alpha \right){\rm{|}}] + {\sigma ^2}} \right\} \end{array} $ | (3) |
考虑不同能量请求用户的公平性,采用对数函数来刻画用户的能量收获效用,而平均单用户的能量收获效用为
| $ U\left( \alpha \right) = \frac{1}{K}\sum\limits_{K = 1}^K {\ln [{E_k}\left( \alpha \right)]} $ | (4) |
在给定能量站的发射功率p/M下,笔者的目的是最大化系统的平均用户能量收获效用,即研究的问题为
| $ \begin{array}{l} \mathop {\max }\limits_\alpha \left\{ {U\left( \alpha \right)} \right\}\\ {\rm{s}}{\rm{.t}}.{\left\| {w\left( \alpha \right)} \right\|^2} = 1 \end{array} $ | (5) |
由于在大规模天线下,用户间的信道具有极限正交特性[4],当采用最大比预编码时,用户间的干扰趋于0,因此,为了简化分析,笔者不考虑信息传输问题. 从上面的系统模型描述可以看出,能量预编码的系数优化问题也就是系统的功率分配问题. 下面针对单能量源和多能量源2种场景分别进行研究.
2 单能量源功率分配方案定理1 在单能量源场景下,能量广播预编码的最优组合系数为
| $ \alpha _k^2 = \frac{1}{{M{\theta _k}}}{[\frac{1}{\lambda } - \frac{{M{\sigma ^2} + p{\theta _k}}}{{Mp{\theta _k}}}]^ + } \approx \frac{1}{{M{\theta _k}}}{[\frac{1}{\lambda } - \frac{{{\sigma ^2}}}{{p{\theta _k}}}]^ + } $ | (6) |
其中[x]+=max {0,x},而λ由式 $ M\sum\limits_{k = 1}^K {\alpha _k^2} {\theta _k} = 1 $决定.
证明 首先推导用户平均效用的表达式,进而再根据约束条件求得平均效用下最优能量预编码的组合系数.
根据概率论知识可得
| $ {\gamma _k} = {\left\| {h_k^T} \right\|^2} \sim \Gamma \left( {m,1} \right) $ | (7) |
而根据文献[7],当hk和hi为相互独立的随机向量时,可得如下的变量分布关系
| $ {\beta _{ki}} = {\left| {\frac{{h_k^T}}{{\left\| {h_k^T} \right\|}}\frac{{h_k^*}}{{\left\| {h_k^*} \right\|}}} \right|^2} \sim B\left( {1,M - 1} \right) $ | (8) |
且βki与γk或γi是相互独立的. 进而利用期望关系E[γk]=M、E[γk2]=M(M+1)和E[βki]=1/M可得
| $ \begin{array}{l} E\left[{{{\left| {g_k^Tw\left( a \right)} \right|}^2}} \right] = E\left[{{{\left| {g_k^T\sum\limits_{i = 1}^K {{\alpha _i}g_i^*} } \right|}^2}} \right] = \\ \alpha _k^2\theta _k^2\left[{{{\left\| {{h_k}} \right\|}^4}} \right] + {\theta _k}\sum\limits_{i = 1,i \ne 1}^K {\alpha _i^2} {\theta _i}E\left[{{{\left\| {h_k^T} \right\|}^2}} \right] \times \\ E\left[{\left| {\frac{{h_k^T}}{{\left\| {h_k^T} \right\|}}\frac{{h_i^*}}{{\left\| {h_i^*} \right\|}}} \right|} \right]E\left[{\left\| {h_i^*} \right\|h2} \right] = \\ \alpha _k^2\theta _k^2{M^2} + M{\theta _k}\sum\limits_{i = 1}^K {\alpha _i^2} {\theta _i} \end{array} $ | (9) |
由大规模天线系统的信道硬化现象
| $ \frac{1}{M}{\left\| {{g_k}} \right\|^2} \to {\theta _k},M \gg 1 $ | (10) |
和不同用户信道的正交性
| $ \frac{1}{M}g_k^Tg_i^* \to 0,k \ne i,M \gg 1 $ | (11) |
式(5)的约束条件为
| $ {\left\| {w\left( \alpha \right)} \right\|^2} = E[{\left\| {w\left( \alpha \right)} \right\|^2}] = M\sum\limits_{i = 1}^K {\alpha _i^2{\theta _i}} = 1 $ | (12) |
因此式(9)重新为
| $ E\left[{{{\left| {g_k^Tw\left( a \right)} \right|}^2}} \right] = \alpha _k^2\theta _k^2{M^2} + {\theta _k} $ | (13) |
进而用户k收获的能量为
| $ {E_k}\left( a \right) = \eta T{\sigma ^2}\left[{\frac{{p{\theta _k}}}{{M{\sigma ^2}}}\left( {\alpha _k^2{M^2}{\theta _k} + 1} \right) + 1} \right] $ | (14) |
平均用户能量收获效用为
| $ \begin{array}{l} U\left( \alpha \right) = \frac{1}{K}\sum\limits_{k = 1}^K {\ln \left[{{E_k}\left( \alpha \right)} \right]} = \ln \left( {\eta T{\sigma ^2}} \right) + \\ \frac{1}{K}\sum\limits_{k = 1}^K {\ln \left[{\frac{{p{\theta _k}}}{{M{\sigma ^2}}}\left( {\alpha _k^2{M^2}{\theta _k} + 1} \right) + 1} \right]} \end{array} $ | (15) |
有了平均用户能量收获效用的表达式,下面求解最优能量预编码的组合系数. 根据式(12)和式(15),式(5)转换为
| $ \begin{array}{l} \mathop {\max }\limits_a \left\{ {\sum\limits_{k = 1}^K {\ln \left[{\frac{{p{\theta _k}}}{{M{\sigma ^2}}}\left( {\alpha _k^2{M^2}{\theta _k} + 1} \right) + 1} \right]} } \right\}\\ {\rm{s}}{\rm{.t}}{\rm{.}}M\sum\limits_{i = 1}^K {\alpha _i^2{\theta _i}} = 1 \end{array} $ | (16) |
上述问题的Lagrange函数为
| $ \begin{array}{l} L\left( {\alpha ;\lambda } \right) = - \sum\limits_{k = 1}^K {\ln \left[{\frac{{p{\theta _k}}}{{M{\sigma ^2}}}\left( {\alpha _k^2{M^2}{\theta _k} + 1} \right) + 1} \right]} + \\ \lambda \left( {M\sum\limits_{i = 1}^K {\alpha _i^2{\theta _i}} - 1} \right) \end{array} $ | (17) |
根据凸优化理论[8],求得式(17)的一阶偏导为
| $ \frac{{\partial L\left( {\alpha ;\lambda } \right)}}{{\partial {\alpha _k}}} = - \frac{{2p{\alpha _k}\theta _k^2M}}{{\frac{p}{M}[\alpha _k^2\theta _k^2{M^2} + {\theta _k}] + {\sigma ^2}}} + 2{\alpha _k}\lambda M{\theta _k} $ | (18) |
令$ \partial L\left( {\alpha ;\lambda } \right)/\partial {\alpha _k} = 0\left( {K = 1,2,\ldots k} \right) $,且考虑问题的约束条件式(12),可得定理.
讨论 将系统的用户按照大尺度衰落θk进行降序排列,当前$ {\tilde K} $个用户的能量预编码组合系数不为0时,根据式(12)可得
| $ \lambda \left( {\tilde K} \right) = \frac{{\tilde K}}{{\left[{1 + \frac{{\tilde K}}{M} + \frac{{{\sigma ^2}}}{p}\sum\limits_{i = 1}^{\tilde K} {\frac{1}{{{\theta _k}}}} } \right]}} $ | (19) |
进而根据式(15)可得$ U(\tilde K) $.由于系统服务的用户数有限,可直接由小到大搜索,直到用户预编码组合系数不为0的假设不成立为止. 此时得到最优用户预编码组合系数不为0的个数为$ {K^ \circ } = \tilde K - 1 $,而其他用户预编码组合系数为0且$ \lambda = \lambda \left( {\tilde K - 1} \right) $.
3 多能量源协作功率分配方案在信息传输系统中,邻区信号对本小区用户信号会造成干扰;而在能量广播系统中,接收到的干扰越大越有利于用户收获更多的能量.在单小区能量广播系统中,没有充分利用邻区干扰信号的能量,因此笔者提出多能量源协作能量传输方案,以提高能量广播系统的平均用户能量收获效用.
假设有L个能量站同时同频服务LK个能量请求用户,从用户k到能量站l的信道向量为glk=θlk1/2hlk,其中θlk和hlk的定义类似于单小区,此处略去.为了获得最大比传输预编码的增益,提出不同能量站给同一用户传输的预编码组合系数相同,即第l个能量站的预编码为
| $ {w_l}\left( \alpha \right) = \sum\limits_{k = 1}^{LK} {{\alpha _k}{g_{lk}}^*} $ | (20) |
记wC(α)=[wT1(α),wT2(α),…,wTL(α)]T,系统的预编码需要满足约束条件‖wC‖2=1. 当L个能量站的总功率约束为Lp/M,所有能量站传输相同符号s时,用户k的接收信号为
| $ {y_k}\left( \alpha \right) = \sum\limits_{l = 1}^L {\sqrt {Lp/Mg} _{lk}^T{w_l}\left( \alpha \right)s} + {n_k} $ | (21) |
利用大规模天线的信道硬化现象和正交特性,用户k在时间TE内收获的能量为
| $ \begin{array}{l} {E_k}\left( \alpha \right) = \eta {T_E}E[|{y_k}\left( \alpha \right){|^2}] \approx \\ \eta {T_E}{\sigma ^2}\left\{ {\frac{{LpM\alpha _k^2}}{{{\sigma ^2}}}{{\left( {\sum\limits_{l = 1}^L {{\theta _{lk}}} } \right)}^2} + 1} \right\} \end{array} $ | (22) |
平均用户的能量收获效用为
| $ \begin{array}{l} {U_c}\left( \alpha \right) = \frac{1}{{LK}}\sum\limits_{k = 1}^{LK} {\ln \left[{{E_k}\left( \alpha \right)} \right]} = \ln \left( {\eta T{\sigma ^2}} \right) + \\ \frac{1}{{LK}}\sum\limits_{k = 1}^{LK} {\ln \left[{\frac{{LpM\alpha _k^2}}{{{\sigma ^2}}}\left( {\sum\limits_{l = 1}^L {{\theta _{lk}}} } \right) + 1} \right]} \end{array} $ | (23) |
根据预编码的约束条件可得
| $ {\left\| {{w_c}\left( \alpha \right)} \right\|^2} = M\sum\limits_{k = 1}^{LK} {\left( {{\alpha _k}^2\sum\limits_{l = 1}^L {{\theta _{lk}}} } \right) = 1} $ | (24) |
统平均用户效用最大化问题为
| $ \begin{array}{l} \mathop {\max }\limits_a \left\{ {\sum\limits_{k = 1}^{LK} {\ln \left[{\frac{{LpM\alpha _k^2}}{{{\sigma ^2}}}{{\left( {\sum\limits_{l = 1}^L {{\theta _{lk}}} } \right)}^2} + 1} \right]} } \right\}\\ {\rm{s}}{\rm{.t}}{\rm{.}}M\sum\limits_{i = 1}^{LK} {{{\left( {{\alpha _k}^2\sum\limits_{l = 1}^L {{\theta _{lk}}} } \right)}_i}} = 1 \end{array} $ | (25) |
定理2 在多能量源协作能量传输情况下,系统的最优能量预编码组合系数为
| $ \alpha _k^2 = \frac{1}{{M\sum\limits_{l = 1}^L {\theta lk} }}{\left[{\frac{1}{\lambda } - \frac{{{\sigma ^2}}}{{Lp}}{{\left( {\sum\limits_{l = 1}^L {{\theta _{lk}}} } \right)}^{ - 1}}} \right]^ + } $ | (26) |
其中参数λ满足约束$ M\sum\limits_{i = 1}^{LK} {{{\left( {{\alpha _k}^2\sum\limits_{l = 1}^L {{\theta _{lk}}} } \right)}_i}} = 1 $.
证明 类似于单能量源的证明过程,此处略.
利用定理2和单能量源场景的讨论方法,可得最终能量预编码组合系数和最优平均用户效用.
4 仿真结果与分析在模拟仿真过程中,假设用户的大尺度衰落系数为θlk=Φdlk-αξlk. 其中:Φ为与天线增益和载波频率有关的常数,dlk为用户k与第l个能量站之间的距离,ξlk为阴影衰落系数且分布为10lg ξlk~CN(0,σSF2). 除去半径为r0的中心圆,每K个用户均匀分布在边长为R的六边形小区中. 仿真中采用归一化噪声功率,即σ2=1,且信噪比定义为p/(Mσ2). 仿真中使用归一化时间,即TE=1. 具体仿真中采用的参数如表 1所示.
| 表1 能量广播系统参数 |
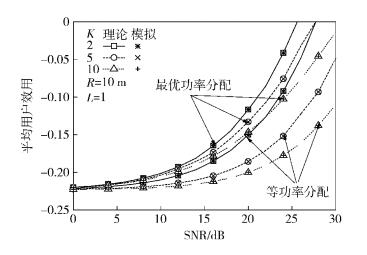
在单能量源场景中,当小区边长R为10 m时,图 2给出了在等功率分配和所提最优功率分配下平均用户效用的对比结果.从图 2可以看出,随着横轴信噪比的增加,每个用户分配到的功率会增加,故每条线代表的平均用户效用会逐渐上升;在相同的用户个数下,与等功率分配相比,所提最优功率分配具有更高的平均用户效用,证明了所提功率分配方案的有效性;在相同功率分配算法和信噪比下,系统的用户个数越多,每个用户分到的功率越小,因此平均用户效用会越低.
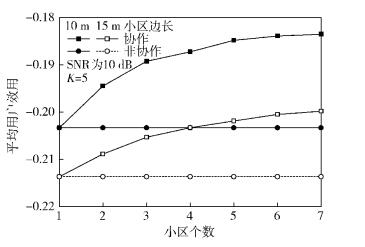
在多能量源场景中,图 3给出了在信噪比为5 dB和每个小区分布5个用户时,协作能量传输和非协作能量传输下平均用户效用的对比. 非协作能量传输结果即为单能量源下的多小区平均结果. 从图 3可以看出,在相同的小区边长下,与非协作能量传输对比,协作能量传输得到的平均用户效用更高,验证了所提协作能量传输方案的有效性;随着小区边长的增加,用户的大尺度衰落更加严重,因此边长为15 m的平均用户效用低于边长为10 m的平均用户效用;随着协作小区个数的增加,平均用户效用逐渐增加,但增加的幅度逐渐减小,同时系统的复杂度也会上升,因此邻区协作是一个复杂度和性能间的折中方案.
5 结束语为了改善下行大规模天线系统中能量广播的平均用户能量收获效用,笔者首先利用大规模天线的性质提出了一种最优功率分配方案.其次考虑到能量传输的特殊性,提出了多能量源协作能量传输方案,推导了协作能量传输下的最优功率分配.仿真结果表明,单能量源中所提功率分配方案的平均用户效用高于等功率分配,多能量源中协作能量传输的平均用户效用好于非协作能量传输,验证了所提2种方案的有效性.
| [1] | Huang Kaibin, Zhou Xiangyun. Cutting the last wires for mobile communications by microwave power transfer[J]. IEEE Communications Magazine, 2015, 53(6):86-93.[引用本文:1]) |
| [2] | Massa A, Oliveri G, Viani F, et al. Array designs for long-distance wireless power transmission:state-of-the-artand innovative solutions[J]. Proceedings of the IEEE, 2013, 101(6):1464-1481.[引用本文:1]) |
| [3] | Krikidis I, Timotheou S, Nikolaou S, et al. Simultaneous wireless information and power transfer in modern communication systems[J]. IEEE Communications Magazine, 2014, 52(11):104-110.[引用本文:1]) |
| [4] | 赵龙, 赵慧, 龙航, 等. 上行大规模天线系统能效分析[J]. 北京邮电大学学报, 2013, 36(6):60-63, 68. Zhao Long, Zhao Hui, Long Hang, et al. Energy efficiency analysis of uplink massive antenna system[J]. Journal of Beijing University of Posts and Telecommunications, 2013, 36(6):60-63, 68.[引用本文:2]) |
| [5] | Xiang Zhengzheng, Tao Meixia, Wang Xiaodong. Massive MIMO multicasting in noncooperative cellular networks[J]. IEEE Journal on Selected Area in Communications, 2014, 32(6):1180-1193.[引用本文:2]) |
| [6] | Zhang Rui, Ho C K. MIMO broadcasting for simultaneous wireless information and power transfer[J]. IEEE Transactions on Wireless Communications, 2013, 12(5):1989-2001.[引用本文:1]) |
| [7] | Lin Shihchun, Chang Tsunghui, Liang Yalan, et al. On the impact of quantized channel feedback in guaranteeing secrecy with artificial noise:the noise leakage problem[J]. IEEE Transactions on Wireless Communications, 2011, 10(3):901-915.[引用本文:1]) |
| [8] | Boyd S, Vandenberghe L. Convex optimization[M]. New York:Cambridge University Press, 2004:100-101, 103.[引用本文:1]) |