关于稀疏表示理论的图像融合主要是利用加权系数方法来确定稀疏系数的融合规则,通过遗传算法求解最优加权系数,实现全色图像和多光谱图像的融合.所提算法与Contourlet变换、主成分分析算法和高通滤波等遥感图像融合算法相比,在提高图像清晰度的同时,光谱保真度相对较高.
Due to sparse nature of the nature of image, the sparse signal representation theory can be well used in image processing, and with sparse representation theory of continuous improvement, it is also widely used in image de-noising rehabilitation and integration process. The sparse representation of image fusion theory was used to determine the weighting factor fusion rules sparse coefficients, and to solve the optimal weighting coefficients of genetic algorithm to achieve image fusion panchromatic, multispectral images, contourlet transform, principal component analysis (PCA) algorithm and the high-pass filter image fusion algorithm. Also it improves the image clarity spectral fidelity compared to other algorithms.
近年来,在国内外发表的有关遥感图像融合技术研究的学术论文中,遥感图像融合的方法正在从粗放、简单向精细、复杂的融合方法转变,并从实验研究的理论模型阶段转化为概括型融合框架阶段,对于遥感图像融合技术的研究大多集中于图像的像素级融合层面上.遥感图像的像素级融合方法可大致分为3类:基于代数运算的遥感图像融合方法、基于空间变换的遥感图像融合方法、基于金字塔式分解和重建的遥感图像融合方法.
近年来,基于稀疏表示理论的图像融合得到了广泛的关注[1, 2]. 笔者针对目前将源图像经过稀疏分解后,稀疏系数的融合规则使用加权系数相对单一的特点,利用遗传算法的寻优特性,对所需权值进行优化,求解出在图像融合中最优的加权系数,然后对图像进行融合. 笔者首先介绍遗传算法,然后介绍稀疏表示理论,研究并论述基于遗传算法优化的稀疏表示遥感图像融合算法,并与不同的融合方法的结果进行对比分析得出结论.
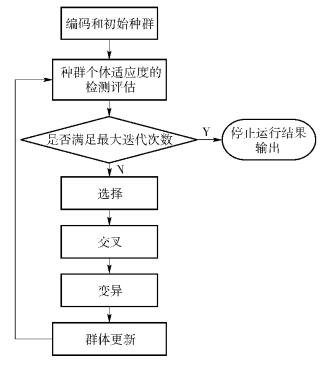
1 遗传算法遗传算法是一种随机优化算法,但它不是简单的随机游动过程,它可以利用已知信息来处理并搜索所要求解的问题,与自然进化相类似,即利用已知的染色体上的基因,搜寻更好的染色体来求解问题.在算法初始阶段,遗传算法对求解实际问题一无所知,通过对每个染色体的评价,并通过相应的适应度的值,使适应度更好的染色体有着更高的繁殖概率,进而获得更好的解的过程. 标准的遗传算法流程如图 1所示.
2 遗传算法优化的稀疏表示图像融合方法在已有的基于稀疏表示的遥感图像融合算法当中,通常是将具有高空间分辨的全色图像和多光谱图像利用常见的稀疏表示的分解方法,获得相应的完备字典和稀疏系数,对于2幅图像中同一地区的稀疏系数应用相应的融合规则,最后再利用完备字典和稀疏系数得出最后的融合结果.在现有的研究中,使用的融合规则有加权系数、绝对值取大和范数取大等规则.绝对值取大和范数取大的方法通常会丢失源图像的某些信息,此外由于在训练字典的过程中,通常将图像进行分块化,当使用绝对值取大和范数取大的方法时,会造成融合结果的块状化非常明显.加权系数效果较好,能很好地克服融合效果的块状化效果,然而如何确定加权系数又受到学者的广泛关注.肖冬杰[3]利用稀疏系数的方差来求解加权系数,其融合效果相对理想.针对加权系数的确定问题,笔者利用遗传算法对加权系数进行优化求解.
由于遗传算法是寻找目标函数解空间中的最优解的过程,所以选取适当的目标函数也尤为重要,Zhou[4]提出了对比2幅图像的扭曲程度的评价系数,Luciano等[5]对此做出了改进,通过引入超复数四元数的概念来对多光谱影像融合进行评价判定,然而由于多光谱影像并不一定都是具有4个波段的影像,对此笔者对多光谱的每个波段和融合结果的对应波段计算相似程度为
| $ {Q_i} = \frac{{4\sigma _{xy}^i{{\bar x}^i}{{\bar y}^i}}}{{\left( {{{\left( {\sigma _x^i} \right)}^2} + {{\left( {\sigma _y^i} \right)}^2}} \right)[{{\left( {{{\bar x}^i}} \right)}^2} + {{\left( {{{\bar y}^i}} \right)}^2}]}} $ | (1) |
其中:$ {\bar x} $为多光谱第i个波段的均值,$ {\bar y} $为融合结果对应第i个波段的均值,σxi为多光谱第i个波段的标准差,σyi为融合结果第i个波段的标准差,σxyi为多光谱和融合结果第i个波段的协方差. 当Qi的取值越接近1时,表明2幅图像相似程度越高.
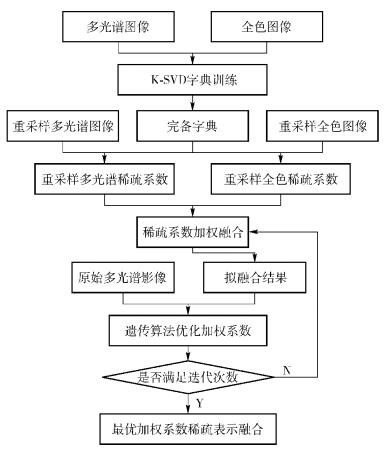
遗传算法优化稀疏表示的融合算法流程如图 2所示.
在遗传算法优化稀疏表示的图像融合算法中,笔者使用QuickBird卫星的全色图像和多光谱图像进行融合,记原始的全色图像为P和多光谱图像为M,首先将原始的全色图像降采样为2.4 m×2.4 m的空间分辨率图像Pi,原始的多光谱图像降采样为9.6 m×9.6 m的空间分辨率图像Mi,然后对P、Pi、M和Mi图像用K奇异值分解(K-SVD,K-singular value decomposition)方法得到图像的过完备字典D,进而利用字典D得出4幅图像的稀疏系数分别为CP、CPi、CM和CMi. 稀疏表示的融合过程为
| $ {C_f} = \alpha {C_{Pi}} + \beta {C_{Mi}} $ | (2) |
其中:Cf为加权得到的稀疏系数,α和β为对应的权值. 用计算得出的稀疏系数Cf和过完备字典D得出拟融合结果,记为图像F,将图像F与图像M相应波段用式(1)计算得出评判数值,式(1)为遗传算法的适应度函数,通过不同种群产生不同的α和β进行迭代进化,最终选出最优的α和β应用于图像P和图像M的稀疏系数的加权融合中,得出最终的融合结果.笔者为了验证遗传算法优化的稀疏表示在图像融合中的应用,对同一数据使用传统的融合方法(如主成分分析(PCA,principal component analysis)[6]、高通滤波[7]和Contourlet变换[8])进行对比实验,对比多种融合算法在不同客观评价指标下的优势,来分析笔者所提算法和其他算法的优缺点.
3 实验结果及分析实验使用QuickBird卫星数据,高空间分辨率图像选取QuickBird卫星的全色图像,其空间分辨率为0.6 m×0.6 m,低空间分辨率图像选取QuickBird卫星的多光谱图像,其空间分辨率为2.4 m×2.4 m,其多光谱图像具有4个波段,波长分别在近红外、红、绿和蓝波长范围内.与经典的融合算法相同,笔者所提融合算法的目的是对全色图像和多光谱图像进行融合,得到具有4个波段和空间分辨率为0.6 m×0.6 m的图像融合结果.实验结果图像如图 3所示.其中:高通滤波融合的滤波半径为r=5;Contourlet变换融合为3阶变换融合;遗传算法(GA,genetic algorithm)优化的稀疏表示融合的种群数为n=20,迭代次数为e=100.
一般情况下,在像素级图像融合方面,为使融合结果既能得到精准的地物分类结果,又能得到便于人工的目视解译效果,因此针对以上2种特性,遥感图像融合的目的在于既能保证原始多光谱图像的光谱信息,又能提高图像的空间分辨率.对于融合质量的好坏,目前采用主观评价和客观评价2种方法,由于在传统的主观评价方法中,评价结果受人为因素影响严重,算法对比评价不能很好地评价哪个算法最优,而在客观的评价方法中,目前还没有完善的统一指标来表明融合质量的好坏,客观的评价方法只能在融合结果的某一个方面进行评价.笔者针对以上情况,并不单一地使用主观评价方法和客观评价方法,而是通过主观的目视和客观的评价指标来综合分析不同融合算法的优缺点.
从目视效果来看,图 3中使用的4种算法的融合结果均使多光谱图像的空间信息得到了增强,其中高通滤波和Contourlet变换在增强图像的纹理特征方面效果显著,然而高通滤波和Contourlet变换出现了明显的光谱畸变. PCA变换、GA优化的稀疏表示在保持多光谱图像的原始光谱特性方面效果显著,同时这2种方法也增强了图像的纹理特征.
在多种客观评价的指标(如均值、标准差和清晰度等)中,目前用来对图像空间信息增强的指标主要有清晰度和信息熵,其中均值和标准差并不能定量地用来分析融合结果的好坏,因此对以上4种算法,笔者计算4种结果的清晰度和信息熵,从客观的角度分析这4种算法在图像空间信息增强的能力,清晰度计算结果如表 1所示,信息熵计算结果如表 2所示.
| 表1 同算法融合结果清晰度 |
从表 1可以看出,高通滤波和Contourlet变换确实与目视效果相一致,这3种方法在提高图像的空间分辨率方面效果明显,相对于原始的多光谱数据,以上4种算法均提高了图像的空间分辨率.
从表 2可以看出,高通滤波和Contourlet变换在提高图像的信息能力方面表现突出,PCA变换提高信息能力方面最弱,其主要原因是在融合算法中,直接用全色图像替换K-L(Karhunen-Loeve)变换得到第一主成分,这样会丢失大量的信息.然而,图像信息熵的提高并不一定说明图像融合的质量最好,因为随着图像中噪声的增加,也会带来图像信息熵的提高.
| 表2 不同算法融合结果信息熵 |
此外,在遥感图像融合质量的客观评价方面,相关系数和光谱扭曲度用来作为衡量图像融合质量评价的重要指标,原因是遥感图像融合的目的在于方便人为的目视解译的同时,需要对融合结果进行地物分类和环境监测,而这些都离不开对光谱曲线的计算,因此保留原始多光谱的光谱信息显得尤为重要,所以在客观评价指标中更为重要的是与原始多光谱相关系数(光谱保真度)和光谱扭曲度(光谱畸变程度).通过与原始多光谱计算得到的相关系数如表 3所示,与原始多光谱计算得到的光谱扭曲度如表 4所示.
| 表3 不同算法融合结果与原始多光谱相关系数 |
| 表4 不同算法的光谱扭曲度 |
从表 3和表 4可以看出,在这4种算法中,高通滤波和Contourlet变换的光谱保真能力和光谱畸变最大,这是因为这2种算法都直接将全色图像的高频信息直接添加到融合结果中,且多光谱的高频信息也被丢失,虽然大量地增加了图像的空间信息,但引入了更多的噪声信息,同时造成了光谱畸变,与以上2种算法不同,GA优化稀疏表示保留了更多原始的多光谱图像信息和全色图像信息,因此图像结果显得更为平滑,其结果在保持了原有光谱信息的基础上,提高了图像的空间分辨率,为实际应用提供了更为有效的方法.
4 结束语立足于遥感图像融合的像素级融合层面,针对特征级和决策级融合,目前国内外研究尚浅,笔者所提算法为图像的特征提取和决策过程提供了新的思路.在笔者所提的基于遗传算法优化的稀疏表示图像融合算法中,目标函数的设定合适与否也相当重要,对于融合结果的客观评价指标还没有统一的评判标准,如果选择一种合理的图像融合评价指标,设定更为合理的目标函数,那么遗传算法在遥感图像融合技术领域的使用将会有更广阔的前景.
| [1] | Iqbal M, Chen Jie, Wen Xianzhong, et al. Remote sensing image fusion using best bases sparse representation[C]//Geoscience and Remote Sensing Symposium (IGARSS), 2012. Munich:IEEE International, 2012, 22(27):5430-5433.[引用本文:1] |
| [2] | 余南南. 基于稀疏表示的图像融合与去噪算法研究[D]. 大连:大连理工大学, 2012.[引用本文:1] |
| [3] | 肖冬杰. 基于稀疏表示的自适应图像融合方法研究[D]. 南昌:南昌航空大学, 2013.[引用本文:1] |
| [4] | Zhou Wang. A universal image quality index[C]//Signal Processing Letters. Storrs:IEEE, 2002, 9(3):81-84.[引用本文:1] |
| [5] | Luciano A, Stefano B. A global quality measurement of pan-sharpened multispectral imagery[C]//Geoscience and Remote Sensing Letters. Alagoas:IEEE, 2004, 1(4):313-317.[引用本文:1] |
| [6] | Richards J A. Remote sensing digital image analysis:an introducion[M]. Berlin Heidelberg, Germany:Springer-Verlag, 2013:267-292.[引用本文:1] |
| [7] | Ranchin T, Wald L. Fusion of high spatial and spectral resolution images:the ARSIS concept and its implementation[J]. Photogrammetric Engineering and Remote Sensing, 2000, 66(1):49-56.[引用本文:1] |
| [8] | Miao Qiguang, Wang Baoshu. A novel image fusion method using Contourlet transform[C]//IEEE Communications, Circuits and Systems Proceedings. Guilin:IEEE, 2006:311-394.[引用本文:1] |