引用本文
王桂宝. 圆形极化阵列到达角和极化参数估计[J]. 北京邮电大学学报, 2016, 39(2): 69-72.  
WANG Gui-bao. Direction of Arrival and Polarization Estimation with a Polarized Circular Array[J]. JOURNAL OF BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS, 2016, 39(2): 69-72.  
Permissions
Copyright©2016, 《北京邮电大学学报》编辑部
《北京邮电大学学报》编辑部 所有
圆形极化阵列到达角和极化参数估计
王桂宝    
陕西理工学院 物理与电信工程学院, 陕西 汉中 723001;
西安电子科技大学 雷达信号处理国防科技重点实验室, 西安 710071
作者简介: 王桂宝(1977-),男,副教授,博士,E-mail:gbwangxd@126.com.
收稿日期: 2015-07-31
基金项目: 国家自然科学基金项目（61475094，61201295）；陕西理工学院院士工作站课题（fckt201504）
摘要

为了放宽布阵条件，解决现有方法存在的相位模糊问题，采用旋转不变信号谱估计算法研究了基于均匀圆形极化阵列的信号参数估计.利用子空间理论，并根据导向矢量的特点得到相邻阵元间的相位差估计，消除了相位模糊；利用沿z轴方向放置的电偶极子阵列导向矢量和磁偶极子阵列导向矢量之间的关系，通过矩阵运算给出了信号极化和到达角估计的最小二乘解，该算法不需要搜索运算和参数配对运算，仿真实验结果验证了该算法的有效性.

关键词: 阵列信号处理    极化敏感阵列    参数估计    子空间    最小二乘         
中图分类号:TN911.23 文献标志码:A 文章编号:20160214 DOI:10.13190/j.jbupt.2016.02.014
Direction of Arrival and Polarization Estimation with a Polarized Circular Array
WANG Gui-bao    
School of Physics and Telecommunication Engineering, Shaanxi University of Technology, Shaanxi Hanzhong 723001, China;
National Laboratory of Radar Signal Processing, Xidian University, Xi'an 710071, China
Abstract

In order to relax the embattle conditions and solve the phase ambiguity of existing algorithm, a signal parameter estimation algorithm based on the polarized uniform circular polarized array was studied using the estimating signal parameters via rotational invariance techniques (ESPRIT) algorithm. The phase differences between two adjacent array elements are obtained based on the performance of steering vector using the subspace theory, the phase ambiguity is resolved. Using the relationship of array manifold vector between z-axis electric dipoles and magnetic dipoles, the least squares solution to the signal polarization and direction of arrival estimations were given with matrix operations without spectral peak searching and parameter matching. Simulations verify the effectiveness of the algorithm.

Key words: array signal processing    polarization sensitive array    parameter estimation    subspace algorithm    least squares    

电磁矢量传感器阵列可获取空间电磁信号的波达方向和极化信息，近来备受人们的关注. 在极化参数估计和误差校正[1, 2, 3, 4, 5, 6]方面，国内外学者取得了许多有价值的研究成果. Wang等[7, 8]提出了利用阵元和圆心的相位差(PDOE，phase difference between origin and element)估计到达角的算法，该算法无相位模糊的条件为圆半径小于最小半波长，该条件导致高频情况下算法失效且布阵困难. 基于旋转不变信号谱估计(ESPRIT，estimating signal parameters via rotational invariance techniques)算法，笔者提出了利用相邻阵元间的相位差(PDAE，phase difference between adjacent elements)估计到达角的算法，扩大了无模糊到达角的估计范围，该算法给出了信号参数估计闭式解，不需要搜索和配对运算，计算量小.

1 信号模型

假设第k(1≤k≤K)个单位功率的完全极化横电磁波通过各向同性的均匀介质入射到电磁矢量传感器上，θk(0≤θk≤π/2)和Φk(0≤Φk≤2π)分别为入射波的俯仰角和方位角，γk(0≤γk≤π/2)和ηk(-π≤ηk≤π)为入射波的极化参数，则传感器输出的电磁场[1]为

$a = \left[\begin{gathered} \sin {\gamma _k}cos{\theta _k}\cos {\phi _k}{e^{{\text{j}}\eta k}} - \cos {\gamma _k}\sin {\phi _k} \hfill \\ \sin {\gamma _k}cos{\theta _k}\sin {\phi _k}{e^{{\text{j}}\eta k}} + \cos {\gamma _k}\cos {\phi _k} \hfill \\ - \sin {\gamma _k}\sin {\theta _k}{e^{{\text{j}}\eta k}} \hfill \\ - \cos {\gamma _k}cos{\theta _k}\cos {\phi _k} - \sin {\gamma _k}\sin {\phi _k}{e^{{\text{j}}\eta k}} \hfill \\ - \cos {\gamma _k}cos{\theta _k}\sin {\phi _k} + \sin {\gamma _k}\cos {\phi _k}{e^{{\text{j}}\eta k}} \hfill \\ \cos {\gamma _k}\sin {\theta _k} \hfill \\ \end{gathered} \right]$ (1)

接收阵列是由N个偶极子对构成的阵列，其阵元是由一个沿z轴方向的电偶极子和一个也沿z轴方向的小磁环组成，N个偶极子对均匀分布在以原点为圆心、R为半径的xOy平面内的圆周上，第1个传感器处于x轴上，沿圆周逆时针方向分别为第0,1,…,N-1个阵元，坐标原点放置1个参考阵元.

此时单个阵元的输出为

$a = \left[\begin{gathered} {e_{kz}} \hfill \\ {h_{kz}} \hfill \\ \end{gathered} \right] = \left[\begin{gathered} - \sin {\theta _k}\sin {\gamma _k}{e^{{\text{j}}\eta k}} \hfill \\ \sin {\theta _k}\cos {\gamma _k} \hfill \\ \end{gathered} \right]$ (2)

N阵元和原点的相位因子构成的空域导向矢量为

${q_k} = \left[\begin{gathered} 1 \hfill \\ q\left( {{\theta _k},{\phi _k},{\varphi _0}} \right) \hfill \\ \vdots \hfill \\ q\left( {{\theta _k},{\phi _k},{\varphi _{N - 1}}} \right) \hfill \\ \end{gathered} \right] = \left[\begin{gathered} 1 \hfill \\ {e^{{\text{j}}\frac{{2\pi R\sin {\theta _k}\cos \left( {{\phi _k} - {\varphi _0}} \right)}}{\lambda }}} \hfill \\ \vdots \hfill \\ {e^{{\text{j}}\frac{{2\pi R\sin {\theta _k}\cos \left( {{\phi _k} - {\varphi _{N - 1}}} \right)}}{\lambda }}} \hfill \\ \end{gathered} \right]$ (3)

其中φn=2πn/N,n=0,1,…,N-1. 从式(3)可以看出，不存在相位模糊的条件为R/λmin ≤0.5，放宽布阵条件,由相邻阵元间的相位因子构成的空域导向矢量为

${{\tilde q}_k} = {q_k}\left( {3:N} \right)/{q_k}\left( {2:N - 1} \right)$ (4)

不存在相位模糊的条件为

$R/{\lambda _{\min }} \leqslant 0.25/\sin \left( {\pi /N} \right)$ (5)

由电偶极子和小磁环构成的子阵导向矢量为

A1=[-sinθ1sinγ1ejη1q1,…,-sinθKsinγKejηKqK]

A2=[sinθ1cosγ1q1,…,sinθKcosγKqK]

比较A1和A2可以发现

${A_2} = {A_1}\Phi $ (6)

$\Phi = {\text{diag}}\left( {\left[{ - {\text{ctg}}{\gamma _{\text{1}}}{e^{ - {\text{j}}\eta 1}},\cdots ,- - {\text{ctg}}{\gamma _k}{e^{ - {\text{j}}\eta k}}} \right]} \right)$ (7)

由Φ可以估计极化参数，在不存在相位模糊的情况下，由式(4)可以估计到达角.

2 信号参数估计算法

将电偶极子阵列和磁偶极子阵列的接收数据顺序排列，得到全阵列的接收数据为

$X\left( t \right) = AS\left( t \right) + N\left( t \right)$ (8)

其中：S(t)为K个互不相关的信号构成的矩阵，N(t)是均值为0、方差为σ2的高斯白噪声，A=[A1;A2].

接收数据的自相关矩阵为

${R_x} = E\left[{X{X^{\text{H}}}} \right] = A{R_s}{A^H} + {\sigma ^2}I$ (9)

其中：E[·]为统计平均，(·)H为转置复共轭操作，Rs=E[S(t1)SH(t1)]为入射信号的自相关函数，对Rx进行特征分解，K个大特征值对应的特征矢量构成信号子空间Es，N-K个小特征值对应的特征矢量构成噪声子空间En，根据子空间理论有

${E_s} = AT = {\left[{{A_1};{A_2}} \right]^T}$ (10)

$\begin{align} & {{E}_{s}}=AT={{\left[ {{A}_{1}};{{A}_{2}} \right]}^{T}} \\ & {{E}_{s1}}={{A}_{1}}T,{{E}_{s2}}={{A}_{2}}T={{A}_{1}}\Phi T \\ & E_{s1}^{\#}{{E}_{s2}}{{T}^{-1}}={{T}^{-1}}\Phi \\ \end{align}$ (11)

对Es1#Es2进行特征分解，特征值构成矩阵${\hat \Phi }$，特征矢量构成矩阵T-1，从而可得

${{\hat \gamma }_k} = {\text{arcctg}}\left( {\left| {{{\hat \Phi }_{kk}}} \right|} \right),{{\hat \eta }_k} = - \arg \left( { - {{\hat \Phi }_{kk}}} \right)$ (12)

${{\hat A}_1} = {E_{s1}}{T^{ - 1}}$ (13)

根据阵列导向矢量${{\hat A}_1}$，得到N个阵元和参考阵元的相位因子构成的空域导向矢量为

${{\hat q}_k} = \frac{{{{\hat A}_1}\left( {:,k} \right)}}{{{A_1}\left( {1,k} \right)}} = \left[{1\;\;{e^{{\text{j}}\frac{{2\pi R\sin {\theta _k}\cos \left( {{\phi _k} - {\phi _0}} \right)}}{\lambda }}} \cdots {e^{{\text{j}}\frac{{2\pi R\sin {\theta _k}\cos \left( {{\phi _k} - {\phi _{N - 1}}} \right)}}{\lambda }}}} \right]$ (14)

相邻阵元间的相位差构成的矢量可表示为

$D = \arg \left[{{{\hat q}_k}\left( {3:N} \right)/{{\hat q}_k}\left( {2:N - 1} \right)} \right]$ (15)

令

$\begin{gathered} {W_1} = \frac{{2\pi R}}{\lambda }\left[\begin{gathered} \;\;\;\;\;\sin \left( {\frac{{2\pi }}{N}} \right)\;\;\;\;\;\;\;\;\;\;\cos \left( {\frac{{2\pi }}{N}} \right) - 1 \hfill \\ \sin \left[{\left( {N - 2} \right)\frac{{2\pi }}{N}} \right]\;\;\cos \left[{\left( {N - 2} \right)\frac{{2\pi }}{N}} \right] - 1 \hfill \\ \end{gathered} \right] \hfill \\ {W_2} = \frac{{2\pi R}}{\lambda }\left[\begin{gathered} \;\;\;\;\;\sin \left( {2\frac{{2\pi }}{N}} \right)\;\;\;\;\;\;\;\;\;\;\cos \left( {2\frac{{2\pi }}{N}} \right) - 1 \hfill \\ \sin \left[{\left( {N - 1} \right)\frac{{2\pi }}{N}} \right]\;\;\cos \left[{\left( {N - 1} \right)\frac{{2\pi }}{N}} \right] - 1 \hfill \\ \end{gathered} \right] \hfill \\ W = {W_2} - {W_1},\Gamma = \left[\begin{gathered} {\Gamma _1} \hfill \\ {\Gamma _2} \hfill \\ \end{gathered} \right] = \left[\begin{gathered} \sin {{\hat \theta }_k}\sin {{\hat \phi }_k} \hfill \\ \sin {{\hat \theta }_k}\cos {{\hat \phi }_k} \hfill \\ \end{gathered} \right] \hfill \\ \end{gathered}$

则有

$\begin{gathered} D = W\Gamma \hfill \\ \left[\begin{gathered} {\Gamma _1} \hfill \\ {\Gamma _2} \hfill \\ \end{gathered} \right] = \left[\begin{gathered} \sin {{\hat \theta }_k}\sin {{\hat \phi }_k} \hfill \\ \sin {{\hat \theta }_k}\cos {{\hat \phi }_k} \hfill \\ \end{gathered} \right] = {W^\# }D \hfill \\ \end{gathered} $ (16)

由式(16)得到信号的俯仰角和方位角估计为

${{\hat \theta }_k} = \arcsin \left( {\sqrt {\Gamma _1^2 + \Gamma _2^2} } \right)$ (17)

$\left. \begin{gathered} {{\hat \phi }_k} = \arcsin \left( {\frac{{{\Gamma _1}}}{{{\Gamma _2}}}} \right),{\Gamma _2} \geqslant 0 \hfill \\ {{\hat \phi }_k} = \pi + \arctan \left( {\frac{{{\Gamma _1}}}{{{\Gamma _2}}}} \right),{\Gamma _2}{\text{ < }}0 \hfill \\ \end{gathered} \right\}$ (18)

3 仿真结果

阵元数为N=16，噪声为相互独立的0均值复高斯随机变量，且与信号不相关，2个非相关的完全极化横电磁波入射信号的俯仰角为[30°,72°]，方位角为[43°,85°]，极化辅助角为[67°,30°]，极化相位差为[80°,120°]，每个信噪比点独立进行Monte Carlo仿真实验200次，每次实验的快拍数为512次，将笔者提出的PDAE算法与PDOE算法作仿真比较.

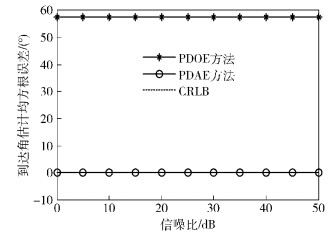
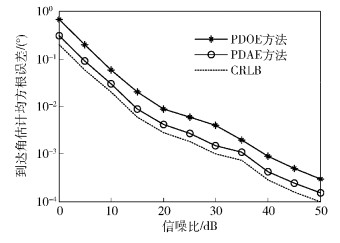
仿真1    圆环半径R=0.9λmin，圆环上相邻2个阵元间隔小于最小半波长，仿真结果如图 1和图 2所示.

图1 到达角估计均方根误差与信噪比的关系

图2 到达角估计的标准偏差随信噪比的变化关系

从图 1可以看出，PDOE算法的估计性能很差，到达角估计均方根误差大于55°，这是由于圆心和阵元间隔大于最小半波长，圆心和阵元间的相位差超出了[-π,π]的范围，从而出现相位模糊，造成到达角估计出错，此时PDOE算法失效. 笔者提出的PDAE算法利用圆环上相邻阵元间的相位差估计到达角，阵元间隔小于最小半波长，相位差在[-π,π]范围内，不存在相位模糊，到达角的估计是正确的.

从图 2可以看出，PDOE算法和PDAE算法的标准偏差几乎一样，说明2种方法的估计值都在平均值附近很小的范围扰动，也就是PDOE算法的估计值都几乎偏离真值55°，而PDAE算法的估计值与真值的偏离程度都在0°附近.

从图 1和图 2可以看出，PDAE算法的估计性能明显优于PDOE算法，且随着信噪比的提高，PDAE算法的估计误差越来越小，越来越接近误差性能下界(CRLB，Cramér-Rao low bound).

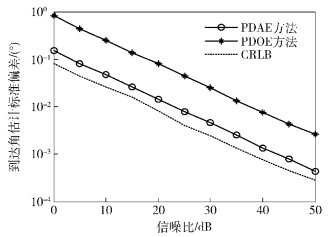
仿真2    圆环半径R=0.5λmin，圆环上相邻2个阵元间隔小于最小半波长，仿真结果如图 3和图 4所示.

图3 到达角估计的均方根误差随信噪比的变化关系

图4 到达角估计的标准偏差随信噪比的变化关系

从图 3和图 4可以看出，PDOE算法与PDAE算法相比较，其到达角估计值与真值的偏离程度更大，且在其均值附近的更大范围内扰动. PDOE算法与PDAE算法均不存在相位模糊，因为2种方法的阵元间隔均小于最小半波长，随着信噪比的提高，2种方法的估计误差越来越小，越来越接近CRLB.

仿真3    圆环半径R=0.9λmin和R=0.5λmin这2种情况的极化参数估计如图 5所示.

图5 极化角估计的标准偏差随信噪比的变化关系

从图 5可以看出，PDOE算法和PDAE算法的极化角估计性能是相同的，2种方法均是利用电偶极子阵列导向矢量和磁偶极子阵列导向矢量之间的关系估计极化参数，极化参数的估计和到达角的估计是独立的，且极化参数的估计精度与阵列孔径无关，阵列稀布对极化参数估计精度没有影响.

4 模糊性分析

由式(3)可得不存在相位模糊的条件为

$R/{\lambda _{\min }} \leqslant 0.5$ (19)

该条件保证圆心和阵元间的距离差小于半波长，相位差小于2π. 由式(4)可知，不存在相位模糊的条件为

$R/{\lambda _{\min }} \leqslant 0.25/\sin \left( {\pi /N} \right)$ (20)

该条件保证圆周上相邻阵元间的距离差小于半波长，相位差小于2π.

当阵元数N < 6时，式(19)比式(20)的条件更宽松，当阵元数N>6时，式(20)比式(19)的条件更宽松. 当阵元数N=6时，2个条件等价. 因此，选择哪个条件进行布阵要由阵元数决定，为了不存在相位模糊，利用式(19)的条件时要取阵元和坐标原点的相位差，利用式(20)的条件时要取圆周上相邻阵元间的相位差，否则上述布阵条件无法保证相位的无模糊.

5 结束语

利用子空间方法研究了基于均匀圆形偶极子对极化阵列的信号到达角和极化参数联合估计算法. 利用相邻阵元间的相位差进行到达角估计，放宽了无相位模糊的条件. 笔者提出的PDAE算法联合利用特征分解的特征值和特征矢量进行参数估计，并给出了信号极化参数和到达角估计的最小二乘解，避免了搜索和配对运算，降低了计算量.

参考文献
[1] Wong Kainamthomas, Yuan Xin. Vector cross-product direction-finding with an electromagnetic vector-sensor of six orthogonally oriented but spatially noncollocating dipoles/loops[J]. IEEE Trans Signal Process, 2011, 59(1):160-171.[引用本文:2]
[2] Yuan Xin. Estimating the DOA and the polarization of a polynomial-phase signal using a single polarized vector-sensor[J]. IEEE Trans Signal Process, 2012, 60(3):1270-1282.[引用本文:1]
[3] Wang Guibao. A joint parameter estimation method with conical conformal CLD pair array[J]. Progress in Electromagnetics Research C, 2015, 57:99-107.[引用本文:1]
[4] 王桂宝, 陶海红, 王兰美. 电偶极子组天线幅相误差校正[J]. 北京邮电大学学报, 2013, 36(5):6-10. Wang Guibao, Tao Haihong, Wang Lanmei. Gain and phase error calibration of a dipole triad antenna[J]. Journal of Beijing University of Posts and Telecommunications, 2013, 36(5):6-10.[引用本文:1]
[5] Zheng Guimei, Wu Bo, Ma Yan, et al. Direction of arrival estimation with a sparse uniform array of orthogonally oriented and spatially separated dipole-triads[J]. IET Radar, Sonar and Navigation, 2014, 8(8):885-894.[引用本文:1]
[6] 陶军, 田彦涛, 崔伟, 等. 基于极化敏感传感器阵列的扩展信号参数估计算法[J]. 仪器仪表学报, 2010, 31(6):1224-1228. Tao Jun, Tian Yantao, Cui Wei, et al. DOA estimation algorithm of scattered sources based on polarization sensitive sensor array[J]. Chinese Journal of Scientific Instrument, 2010, 31(6):1224-1228.[引用本文:1]
[7] Wang Lanmei, Chen Zhihai, Wang Guibao, et al. Estimating DOA and polarization with spatially spread loop and dipole pair array[J]. Journal of System Engineering and Electronics, 2015, 26(1):44-49.[引用本文:1]
[8] 许远. 基于圆形极化阵列的信号多参数估计[D]. 长春:长春理工大学, 2008.[引用本文:1]