2. 大庆石化建设公司 仪表一分公司, 黑龙江 大庆 163714
针对恒模信号,将概率约束稳健算法与恒模算法相结合,提出一种新的稳健自适应波束形成算法.先将导向偏差分为高斯随机分布和未知分布2种场景,分别建立优化代价函数,并将该优化问题转化为二阶锥规划问题,运用内点法高效求解.然后对算法求解的全局最优性进行理论分析.在数值仿真部分,用所提算法与相关稳健算法作对比仿真,验证该算法的优越性和有效性.
2. Instrument First Branch, Daqing Petrochemical Construction Company, Heilongjiang Daqing 163714, China
This article combines probability-constrained optimization technique with constant modulus algorithm to study a new robust adaptive beamforming algorithm for constant modulus signals. Aiming at the two kinds of cases that steering vector mismatch follows the Gauss distribution and unknown distribution, the optimization cost functions are respectively built, and these optimization problems are changed to the second order cone (SOC) programming ones solved with interior point methods. Then, the convex analyses of the optimization problems are carried out as well. In the simulation, the proposed algorithm compares with related robust algorithms to demonstrate its superiority and effectiveness.
稳健自适应波束形成技术一直是阵列信号处理领域研究的热点问题. 当前经典的稳健波束形成方法主要有对角加载法、特征空间法[1]、导向矢量估计法[2]、最差情况最优法[3]和概率约束稳健算法[4]. 最差情况最优法以实现简便、性能优良为特点,得到人们的广泛关注,但最差情况的约束范围较大,不容易获得较高的信干噪比(SINR,signal-to-interference-plus-noise ratio);而在某些实际应用场景中,导向偏差分布的先验信息已知,概率约束稳健算法能取得更好的效果. 笔者利用恒模信号的恒模特性,将概率约束稳健算法与恒模算法相结合,提出一种新的基于概率约束的稳健自适应波束形成算法.
1 阵列模型假定M元全向均匀线阵,接收N个远场窄带信号,令x(i)=[x1(i),…,xM(i)]T∈CM×1为第i拍的接收数据,则可表示为
| $\begin{gathered} x\left( i \right) = \sum\limits_{k = 0}^{N - 1} {{s_k}\left( i \right){a_k} + n\left( i \right)} = \hfill \\ {s_0}{a_0} + \sum\limits_{k = 0}^{N - 1} {{s_k}\left( i \right){a_k} + n\left( i \right)} = \hfill \\ {x_0}\left( i \right) + {x_{\operatorname{int} }}\left( i \right) + n\left( i \right) \hfill \\ \end{gathered} $ | (1) |
其中:sk(i)和${a_k} = {\left[{1,{e^{ - 2\pi {\text{j}}\frac{d}{\lambda }\cos {\theta _k}}},\cdots ,{e^{ - 2\pi {\text{j}}\left( {M - 1} \right)\frac{d}{\lambda }\cos {\theta _k}}}} \right]^{\text{T}}}$为第k个信号波形及其导向矢量,θk,k=0,1,…,N-1为信号的波达角,d=λ/2为阵元间距,λ为波长,x0(i)为有用信号向量,xint(i)为干扰信号向量,n(i)∈CM×1为高斯白噪声向量.
波束形成器的输出为
| $y\left( i \right) = {w^{\text{H}}}x\left( i \right)$ | (2) |
其中w=[w1,…,wM]T∈CM×1为波束形成的权矢量. 阵列的输出SINR为
| $\frac{{\sigma _0^2{{\left| {{w^{\text{H}}}{a_0}} \right|}^2}}}{{{w^{\text{H}}}{R_{i + n}}w}}$ | (3) |
其中:σ02为有用信号功率,Ri+n为干扰加噪声协方差,其表达式为
| ${R_{i + n}} = E\left\{ {\left( {{x_{\operatorname{int} }}\left( i \right) + n\left( i \right)} \right){{\left( {{x_{\operatorname{int} }}\left( i \right) + n\left( i \right)} \right)}^{\text{H}}}} \right\}$ | (4) |
在实际应用中,Ri+n不容易获得,常代替为
| $\hat R = \frac{1}{Q}\sum\limits_{i = 1}^Q {x\left( i \right){x^{\text{H}}}\left( i \right)} $ | (5) |
其中Q为采样快拍数.
2 概率约束稳健波束形成算法概率约束最小方差波束形成算法对导向矢量施加概率约束条件,且只对高概率事件保持无畸变响应,不同于最差情况最优法,对所有情况都保持约束. 假定导向矢量偏差e为未知的随机变量,概率约束最小方差波束形成问题的表达式为
| $\begin{gathered} \mathop {\min }\limits_w {w^{\text{H}}}\hat Rw \hfill \\ {\text{s}}{\text{.t}}{\text{.Pr}}\left\{ {\left| {{w^{\text{H}}}\tilde a} \right| \geqslant \delta } \right\} \geqslant p \hfill \\ \end{gathered} $ | (6) |
其中:Pr {·}为概率函数,p为概率值,δ为常系数,通常设为1,$\tilde a$=a+e为假定导向矢量. 式(6)表示在附加随机约束的条件下,使波束形成输出功率最小化. 利用柯西-许瓦兹不等式,由式(6)可得
| $\begin{gathered} \mathop {\min }\limits_w {w^{\text{H}}}\hat Rw \hfill \\ {\text{s}}{\text{.t}}{\text{.Pr}}\left\{ {\left| {{w^{\text{H}}}e} \right| \leqslant \left| {{w^{\text{H}}}a} \right| - \delta } \right\} \geqslant p \hfill \\ \end{gathered} $ | (7) |
根据应用场景不同,将导向矢量偏差e的概率密度函数分为2种情况研究:一种是针对莱斯信道场景,假设e服从0均值圆对称复高斯分布;另一种是针对e的概率分布为未知的场景.
2.1 偏差为复高斯分布场景假设e服从均值为0,方差为Ce的圆对称复高斯随机分布,即
| $e~{N_c}\left( {{0_M},{C_e}} \right)$ | (8) |
其中0M为M×1维零向量.
协方差矩阵Ce为导向矢量偏差的二阶统计量. 在许多应用场景[5]中,可将协方差矩阵表示为对角阵的形式,而对于Ce在一些场景为非对角阵的情况,可通过变换,使其近似对角化.
由式(8)可得
| ${w^{\text{H}}}\left( {a + e} \right)~{N_c}\left( {{w^{\text{H}}}a,{{\left\| {C_e^{1/2}w} \right\|}^2}} \right)$ | (9) |
如果x、y为2个独立、同分布、0均值,且方差为σ2的高斯随机变量,则$z = \sqrt {{x^2} + {y^2}} $的累积分布函数为
| $F\left( z \right) = 1 - {e^{ - {z^2}/2{\sigma ^2}}}$ | (10) |
因而,可将式(7)的约束条件写为
| $\begin{gathered} \Pr \left\{ {\left| {{w^H}e} \right| \leqslant \left| {{w^H}a} \right| - \delta } \right\} = \hfill \\ 1 - \exp \left( { - \frac{{{{\left( {\left| {{w^{\text{H}}}a} \right| - \delta } \right)}^2}}}{{{{\left\| {C_\delta ^{1/2}w} \right\|}^2}}}} \right) \geqslant p \hfill \\ \end{gathered} $ | (11) |
即可推得
| $\left\| {C_e^{1/2}w} \right\| \leqslant \frac{1}{{\sqrt { - \ln \left( {1 - p} \right)} }}\left( {\left| {{w^{\text{H}}}a} \right| - \delta } \right)$ | (12) |
因为任意改变w的相位不影响式(6)的目标函数值,所以可令
| $\operatorname{Re} \left\{ {{w^{\text{H}}}a} \right\} \geqslant 0,\operatorname{Im} \left\{ {{w^{\text{H}}}a} \right\} = 0$ | (13) |
因而,可将式(6)写为
| ${\text{s}}{\text{.t}}{\text{.}}\left\| {C_e^{1/2}w} \right\| \leqslant \frac{1}{{\sqrt { - \ln \left( {1 - p} \right)} }}\left( {{w^{\text{H}}}a - \delta } \right)$ | (14) |
如果导向矢量偏差e的概率分布为未知,则需要考虑最差不匹配,即概率值Pr {|wHe|≤|wHa|-δ}为最小的情况. 假设存在一个均值为0,方差为σξ2的随机变量ξ,对于任意正实数α,由切比雪夫不等式可得
| $\Pr \left\{ {\left| \xi \right| \geqslant a} \right\} \leqslant \frac{{\sigma _\xi ^2}}{{{\alpha ^2}}}$ | (15) |
因而,Pr {|wHe|≤wHa-δ}≥p的下边界表示为
| $\inf \Pr \left\{ {\left| {{w^{\text{H}}}e} \right|{\text{ < }}{w^{\text{H}}}a - \delta } \right\} = 1 - \frac{{{{\left\| {C_e^{1/2}w} \right\|}^2}}}{{\left( {{w^{\text{H}}}a - \delta } \right)}}$ | (16) |
对于e为任意分布
| $ {\left\| {C_e^{1/2}w} \right\|^2}{\text{ < }}{\left( {{w^{\text{H}}}a - \delta } \right)^2}$ | (17) |
都成立. 所以,在该场景下,式(6)的优化问题可表示为
| ${\text{s}}{\text{.t}}{\text{.}}\left\| {C_e^{1/2}w} \right\| \leqslant \sqrt {1 - p} \left( {{w^{\text{H}}}a - \delta } \right)$ | (18) |
在无线通信系统中,各种环境干扰和多径效应的存在,使接收信号产生幅值的波动. 恒模算法利用了恒模信号的恒包络特性,使阵列输出保持在恒定的幅值,起到抑制干扰的作用. 恒模算法[6, 7]的代价函数为
| $J\left( {p,q} \right) = E\left[{{{\left( {{{\left| {y\left( i \right)} \right|}^p} - r} \right)}^q}} \right]$ | (19) |
其中:y(i)为阵列输出,r为有用信号的恒模值,p和q为预设参数,通常设置p=2,q=2,E[·]为期望,|·|为绝对值,i为采样快拍.
3.2 优化问题的形成采用文献[6]的方法,当快拍数较多时,
| ${w^{\text{H}}}\left( i \right)x\left( i \right) \approx {w^{\text{H}}}\left( {i - 1} \right)x\left( i \right)$ |
因而式(19)可近似表示为
| $\begin{gathered} J = E\left[{\left( {{{\left| {y\left( i \right)} \right|}^2} - {r^2}} \right)} \right] = \hfill \\ E\left\{ {{{\left( {{w^{\text{H}}}\left( i \right)x\left( i \right){x^{\text{H}}}\left( i \right)w\left( i \right) - r} \right)}^2}} \right\} \approx \hfill \\ E\left\{ \begin{gathered} {\left( {{w^{\text{H}}}\left( i \right)x\left( i \right){x^{\text{H}}}\left( i \right)w\left( {i - 1} \right) - r} \right)^{\text{H}}} \times \hfill \\ \left( {{w^{\text{H}}}\left( {i - 1} \right)x\left( i \right){x^{\text{H}}}\left( i \right)w\left( i \right) - r} \right) \hfill \\ \end{gathered} \right\} = \hfill \\ {w^{\text{H}}}E\left\{ {{{\left| {y\left( i \right)} \right|}^2}x\left( i \right){x^{\text{H}}}\left( i \right)} \right\}w - \hfill \\ 2r\operatorname{Re} \left\{ {{w^{\text{H}}}E\left\{ {{y^ * }\left( i \right)x\left( i \right)} \right\}} \right\} \hfill \\ \end{gathered} $ | (20) |
其中y(i)=wH(i-1)x(i). 因此,偏差为复高斯分布场景的优化问题可表示为
| $\begin{gathered} \mathop {\min }\limits_w {w^{\text{H}}}{R_a}w - 2r\operatorname{Re} \left\{ {{d^{\text{H}}}w} \right\} \hfill \\ {\text{s}}{\text{.t}}{\text{.}}\left\| {C_e^{1/2}w} \right\| \leqslant \frac{1}{{\sqrt { - \ln \left( {1 - p} \right)} }}\left( {{w^{\text{H}}}a - \delta } \right) \hfill \\ \end{gathered} $ | (21) |
偏差为未知分布场景的优化问题可表示为
| $\begin{gathered} \mathop {\min }\limits_w {w^{\text{H}}}{R_a}w - 2r\operatorname{Re} \left\{ {{d^{\text{H}}}w} \right\} \hfill \\ {\text{s}}{\text{.t}}{\text{.}}\left\| {C_e^{1/2}w} \right\| \leqslant \sqrt {1 - p} \left( {{w^{\text{H}}}a - \delta } \right) \hfill \\ \end{gathered} $ | (22) |
其中
| $\begin{gathered} {R_a} = E\left\{ {{{\left| {y\left( i \right)} \right|}^2}x\left( i \right){x^{\text{H}}}\left( i \right)} \right\} \hfill \\ d = E\left\{ {{y^ * }\left( i \right)x\left( i \right)} \right\} \hfill \\ \end{gathered} $ |
1) 初始化
| $ {R_a}\left( 0 \right) = \sigma _n^2I$ | (23) |
| $d\left( 0 \right) = 0$ | (24) |
| $w\left( 0 \right) = a/M$ | (25) |
2) 参数Ra(i)和d(i)的迭代更新
| $y\left( i \right) = {w^{\text{H}}}\left( {i - 1} \right)x\left( i \right)$ | (26) |
| ${R_a}\left( i \right) = \mu {R_a}\left( {i - 1} \right) + {\left| {y\left( i \right)} \right|^2}x\left( i \right){x^{\text{H}}}\left( i \right)$ | (27) |
| $d\left( i \right) = \mu d\left( {i - 1} \right) + x\left( i \right){y^ * }\left( i \right)$ | (28) |
其中μ∈(0,1)为迭代的遗忘因子.
3) 优化问题的求解
根据式(21)和式(22)优化问题的表达式,利用二阶锥(SOC,second order cone)规划实现最优解的求取. 关于该解的全局最优性将在第4节进行分析.
在式(21)的约束条件中,Ce为对角阵,不妨设为${C_e} = \frac{{\sigma _e^2}}{M}{I_M}$. 其中:IM为M阶单位阵,σe2为导向向量偏差e的方差,于是可将式(21)变为
| $\begin{gathered} \mathop {\min }\limits_w {w^{\text{H}}}{R_a}w - 2r\operatorname{Re} \left\{ {{d^{\text{H}}}w} \right\} \hfill \\ {\text{s}}{\text{.t}}{\text{.}}\beta \left\| w \right\| \leqslant {w^{\text{H}}}a - \delta \hfill \\ \end{gathered} $ | (29) |
其中$\beta = {\sigma _e}\sqrt {\frac{{ - \ln \left( {1 - p} \right)}}{M}} $为常系数.
再使用克罗内克分解Ra=RacHRac,将式(29)用SOC规划求解的形式表示为
| $\begin{gathered} \mathop {\min }\limits_{\tau ,w} \tau \hfill \\ {\text{s}}{\text{.t}}{\text{.}}{w^{\text{H}}}R_{ac}^{\text{H}}{R_{ac}}w - 2r\operatorname{Re} \left\{ {{d^{\text{H}}}w} \right\} \leqslant \tau \hfill \\ {w^{\text{H}}}a - \delta \geqslant \beta {\left\| w \right\|_2} \hfill \\ \end{gathered} $ | (30) |
然后,将式(30)用标准形式表示为
| $\begin{gathered} \mathop {\min }\limits_{\tau ,w} \tau \hfill \\ {\text{s}}{\text{.t}}{\text{.}}\frac{1}{2} + r{d^{\text{H}}}w + \frac{\tau }{2} \geqslant \left\| {\left[\begin{gathered} \frac{1}{2} - r{d^{\text{H}}}w - \frac{\tau }{2} \hfill \\ {R_{ac}}w \hfill \\ \end{gathered} \right]} \right\| \hfill \\ {w^{\text{H}}}a - \delta \geqslant \beta {\left\| w \right\|_2} \hfill \\ \end{gathered} $ | (31) |
笔者选用高效优化求解工具包Sedumi进行求解,将式(31)用工具包[8]要求的形式表示为
| $\begin{gathered} \mathop {\min }\limits_u {p^{\text{T}}}u \hfill \\ {\text{s}}{\text{.t}}{\text{.}}f + {F^{\text{T}}}u \in S_1^{M + 2}S_2^{M + 1} \hfill \\ \end{gathered} $ | (32) |
其中
| $\begin{gathered} p = \left[{1,{0^{\text{T}}}} \right] \in {R^{\left( {M + 1} \right) \times 1}} \hfill \\ u = \left[{\tau ;w} \right] \in {R^{\left( {M + 1} \right) \times 1}} \hfill \\ f = {\left[{1/2,1/2,{0^{\text{T}}},- \delta ,{0^{\text{T}}}} \right]^{\text{T}}} \in {R^{\left( {2M + 3} \right) \times 1}} \hfill \\ {F^{\text{T}}} = \left[\begin{gathered} \;\;\frac{1}{2}\;\;\;\;r{d^{\text{H}}} \hfill \\ - \frac{1}{2}\;\; - r{d^{\text{H}}} \hfill \\ \;\;\;0\;\;\;\;\;{R_{ac}} \hfill \\ \;\;\;0\;\;\;\;\;{a^{\text{H}}} \hfill \\ \;\;\;0\;\;\;\;\;\beta I \hfill \\ \end{gathered} \right] \hfill \\ \end{gathered} $ |
S1M+2和S2M+1分别为M+2维和M+1维的SOC集合.
式(22)优化问题的实现过程与式(21)类似,在这里不再赘述.
4 全局最优解存在性分析判断所提算法的解是否具有全局最优性,只需判断所提算法目标函数的凸性,即判断式(21)和式(22)优化问题的海森矩阵是否是半正定的,式(21)和式(22)的分析方式相同,下面以式(21)为例进行分析.
因为该优化问题的最优解存在于约束边界处,为了便于分析,利用式(29)的约束条件β‖w‖=wHa-δ,将w写为
| $w = \frac{a}{M}\left( {\delta + \beta \left\| w \right\|} \right) + Bz$ | (33) |
其中:z∈CM×1,B的列向量为aH的单位0空间,aHa=M.
由式
| ${\left\| w \right\|_2} = \tau = \sqrt {\frac{1}{M}{{\left( {\delta + \beta \tau } \right)}^2} + {z^{\text{H}}}z} $ | (34) |
推得
| $\tau = \frac{{\beta \delta }}{{M - {\beta ^2}}} + \sqrt {\frac{{M{z^{\text{H}}}z + {\delta ^2}}}{{M - {\beta ^2}}} + {{\left( {\frac{{\beta \delta }}{{M - {\beta ^2}}}} \right)}^2}}$ | (35) |
因而,将w用以z为自变量的函数表示为
| $w\left( z \right) = \frac{a}{M}\left( \begin{gathered} \delta + \frac{{{\beta ^2}\delta }}{{M - {\beta ^2}}} + \hfill \\ \beta \sqrt {\frac{{M{z^{\text{H}}}z + {\delta ^2}}}{{M - {\beta ^2}}} + {{\left( {\frac{{\beta \delta }}{{M - {\beta ^2}}}} \right)}^2}} \hfill \\ \end{gathered} \right) + Bz$ | (36) |
代入到恒模算法的目标函数为
| $\begin{gathered} J = E\left\{ {{{\left| {y\left( i \right)} \right|}^2} - r} \right\} = \hfill \\ E\left\{ {{{\left[{{w^{\text{H}}}\left( z \right)x{x^{\text{H}}}w\left( z \right) - r} \right]}^2}} \right\} \hfill \\ \end{gathered} $ | (37) |
因而,海森矩阵H为
| $\begin{gathered} H = 2\frac{\partial }{{\partial {z^{\text{H}}}}}\left( {E\left\{ {{{\left| {y\left( i \right)} \right|}^2} - r} \right\}} \right)\frac{\partial }{{\partial z}}\left( {E\left\{ {{{\left| {y\left( i \right)} \right|}^2} - r} \right\}} \right) + \hfill \\ 2E\left\{ {{{\left| {y\left( i \right)} \right|}^2} - r} \right\}\frac{\partial }{{\partial {z^{\text{H}}}}}\frac{\partial }{{\partial z}}\left( {E\left\{ {{{\left| {y\left( i \right)} \right|}^2} - r} \right\}} \right) \hfill \\ \end{gathered} $ | (38) |
考虑如果E{|y(i)|2-r}≥0,则H的第1项满足半正定,将第2项展开得
| ${H_2} = E\left\{ \begin{gathered} {\left( { - \frac{\beta }{2}\left( {\frac{1}{{\sqrt \phi }}} \right)} \right)^3}{\left( {\frac{M}{{M - {\beta ^2}}}} \right)^2}\operatorname{Re} \left\{ \eta \right\}z{z^{\text{H}}} + \hfill \\ \beta \frac{1}{{\sqrt \phi }}\left( {\frac{M}{{M - {\beta ^2}}}} \right)\operatorname{Re} \left\{ \eta \right\}{I_{M - 1}} + \hfill \\ \frac{\beta }{2}\frac{1}{{\sqrt \phi }}\left( {\frac{M}{{M - {\beta ^2}}}} \right)\frac{{{a^{\text{H}}}}}{M}x{x^{\text{H}}}\frac{a}{M}\frac{\beta }{2}\frac{1}{{\sqrt \phi }}\left( {\frac{M}{{M - {\beta ^2}}}} \right)z{z^{\text{H}}} + \hfill \\ \left( {\frac{\beta }{2}\frac{1}{{\sqrt \phi }}\left( {\frac{M}{{M - {\beta ^2}}}} \right)z\frac{{{a^{\text{H}}}}}{M} + {B^{\text{H}}}} \right)x{x^{\text{H}}} \times \hfill \\ \left( {\frac{a}{M}\frac{\beta }{2}\frac{1}{{\sqrt \phi }}\left( {\frac{M}{{M - {\beta ^2}}}} \right){z^{\text{H}}} + B} \right) \hfill \\ \end{gathered} \right\}$ | (39) |
其中
| $\begin{gathered} \phi = \left( {\frac{{M{z^{\text{H}}}z + {\delta ^2}}}{{M - {\beta ^2}}} + {{\left( {\frac{{\beta \delta }}{{M - \beta }}} \right)}^2}} \right) \hfill \\ \eta = \frac{{{a^{\text{H}}}}}{M}x{x^{\text{H}}}\left( {\phi \frac{a}{M} + Bz} \right) \hfill \\ \phi = \left( {\delta + \frac{{{\beta ^2}\delta }}{{M - \beta }} + \beta \sqrt \phi } \right) \hfill \\ \end{gathered} $ |
假设
| $\operatorname{Re} \left\{ \eta \right\} = \operatorname{Re} \left\{ {\frac{{{a^{\text{H}}}}}{M}x{x^{\text{H}}}\left( {\phi \frac{a}{M} + Bz} \right)} \right\} \geqslant 0$ | (40) |
该假设是可行的,只要xHBz可补偿${x^{\text{H}}}\phi \frac{a}{M}$的值,因此式(40)除了第1项皆为半正定,令H2的4项分别表示为H2,1,…,H2,4,如果满足
| ${{v}^{\operatorname{H}}}{{H}_{2,2}}v\ge -{{v}^{\text{H}}}{{H}_{2,1}}v$ | (41) |
则H2满足半正定条件. 其中:v为与z有相同范数的任意向量,即zHz=vHv且-zHH2,1z为-vHH2,1v的上界. 将其展开、整理,可得
| $2\left( {\frac{{M{z^{\text{H}}}z + \delta }}{{M - {\beta ^2}}} + {{\left( {\frac{{\beta \delta }}{{M - {\beta ^2}}}} \right)}^2}} \right) \geqslant \left( {\frac{{M{z^{\text{H}}}z}}{{M - {\beta ^2}}}} \right)$ | (42) |
式(42)显然成立,得证式(41)成立,即可得证在E{|y(i)|2-r}≥0的条件下,存在全局最优解. 若保证该不等式成立,只需满足r≤δE{|s0|2},即可保证所求解为全局最优解.
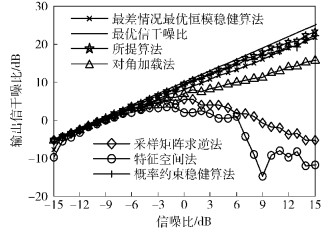
5 算法仿真一个等距均匀线阵,阵元数为M=10,阵元间距为半波长,有用信号方向为3°,2个干扰信号的波达角分别为30°和50°,干扰信号相对于有用信号的功率为7 dB,噪声为高斯白噪声,噪声相对于有用信号的功率为0,选用对角加载法、特征空间法、采样矩阵求逆法、概率约束稳健算法[4]、最差情况最优恒模稳健算法[7]和所提算法作对比仿真,分为2部分,实验1和2是在偏差为复高斯分布场景下的仿真,实验3和4是在偏差为未知分布场景下的仿真.
选用的相干干扰模型和非相干干扰模型分别为
| $e = \frac{{{\sigma _e}}}{{\sqrt {ML} }}\sum\limits_{l = 1}^L {{e^{{\text{j}}\vartheta l}}a\left( {{\theta _0} + {\theta _l}} \right)} $ | (43) |
和
| $e = \frac{{{\sigma _e}}}{{\sqrt {ML} }}\sum\limits_{l = 1}^L {{C_l}\left( i \right)a\left( {{\theta _0} + {\theta _l}} \right)} $ | (44) |
相关参数的设置为|s0|=1,δ=1,μ=0.998,p=0.95,Ce=${C_e} = \frac{{\sigma _e^2}}{M}{I_M}$,σe2=0.3M,L=4,θl服从均值为3°、标准差为2°的均匀分布,vl服从在[0,2π]之间的均匀分布,Cl(k)是均值为0,方差为1的圆对称复高斯随机变量,对应的快拍i独立产生. 每次仿真,相干干扰模型中的vl和θl在每个快拍不产生变化,但每次运行都发生改变. 非相干干扰模型中的Cl(k)和θl在每次运行和每个快拍都发生改变.
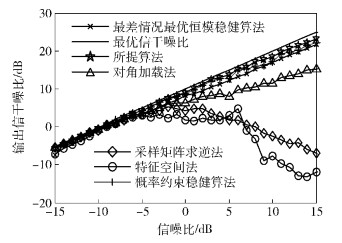
在偏差为复高斯分布场景下,实验1为相干扰动,实验2为非相干扰动. 图 1和图 2为对应于快拍i=200时的输出SINR随输入信噪比(SNR,signal noise ratio)的变化情况. 从图 1和图 2可以看出,所提算法在相干干扰和非相干干扰条件下,随着输入SNR的增大,对比算法之间的SINR差异逐渐明显,所提算法的性能优于其他算法,并近似于最优SINR曲线. 还可以观察到,随着输入SNR的增加,所提算法相比于概率约束稳健算法,SINR性能提升了大约1 dB.
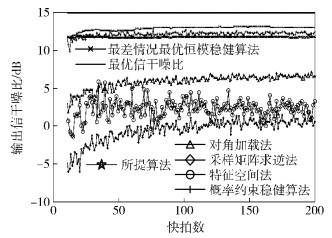
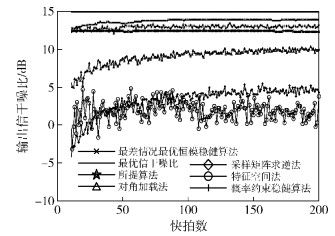
在偏差为未知分布场景下,有用信号为5 dB. 实验3为相干扰动,实验4为非相干扰动. 图 3和图 4给出了SINR随快拍的变化情况. 从图 3和图 4可以看出,在比较的6种算法中,所提算法在收敛SINR和收敛数值稳定性上都具有较好的性能,并近似于最优SINR曲线. 还可以观察到,由于最差情况最优恒模稳健算法和所提算法都利用了有用信号的恒模特性,因而获得了较平稳的收敛数值,但由于前者未利用导向偏差的先验概率信息,所以只达到了相对较低的SINR. 所提算法与概率约束稳健算法相比,由于利用了有用信号的恒模特性,所以在SINR随快拍收敛后,获得了约1 dB的SINR提升.
6 结束语
实际应用中,导向偏差的先验分布是已知的,而最差情况最优算法的“最差情况”不常发生,过于严格的约束会导致SINR性能的下降. 针对这种情况,概率约束稳健波束形成算法更具有实际价值. 所提算法将概率约束稳健算法与恒模算法相结合,提出一种针对恒模信号的稳健波束形成算法. 在导向偏差为高斯分布和未知分布2种场景下,分别形成优化代价函数,运用凸优化理论精确求解,并对求解的全局最优性进行理论分析. 在仿真部分,验证了所提算法在输出SINR和稳健性方面具有较好的性能. 在一些具有恒模信号的无线通信系统中,所提算法具有广泛的应用价值.
| [1] | Huang Fei, Sheng Weixing, Ma Xiaofeng. Modified projection approach for robust adaptive array beamforming[J]. Signal Processing, 2012, 92(7):1758-1763.[引用本文:1] |
| [2] | Hassanien A, Vorobyov S A, Wong Konmax. Robust adaptive beamforming using sequential quadratic programming:an iterative solution to the mismatch problem[J]. IEEE Signal Processing Letters, 2008, 15:733-736.[引用本文:1] |
| [3] | Vorobyov S A, Gershman A B, Luo Zhiquan. Robust adaptive beamforming using worst-case performance optimization:a solution to the signal mismatch problem[J]. IEEE Transactions on Signal Processing, 2003, 51(2):313-324.[引用本文:1] |
| [4] | Vorobyov S A, Rong Yue, Gershman A B. Robust adaptive beamforming using probablitity-constrained optimization[C]//IEEE/SP 13th Workshop on Statistical Signal Processing, 2005:934-939.[引用本文:2] |
| [5] | Fuks G, Goldberg J, Messer H. Bearing estimation in a Ricean channel I inherent accuracy limitations[J]. IEEE Transactions on Signal Processing, 2001, 49(5):925-937.[引用本文:1] |
| [6] | Chen Yuxin, Le-Ngoc T, Champagne B, et al. Recursive least squares constant modulus algorithm for blind adaptive array[J]. IEEE Transactions on Signal Processing, 2004, 52(5):1452-1456.[引用本文:2] |
| [7] | Landau L, De L R C, Haardt M. Robust adaptive beamforming using worst-case optimization with constrained constant modulus criterion[C]//IEEE 17th International Conference on Digital Signal Processing (DSP), 2011:1-6.[引用本文:2] |
| [8] | Sturm J F. Using SeDuMi 1.02, a matlab toolbox for optimization over symmetric cones[J]. Optimization Methods and Software, 1999, 11(1-4):625-653.[引用本文:1] |