2. 西安交通大学 电子与信息工程学院, 西安 710049;
3. 西安邮电大学 通信与信息工程学院, 西安 710061
针对网络流量的非线性和多维度动力学特性,结合小波多尺度分析的能力,提出了基于Morlet小波核函数的支持向量机回归算法(Morlet-SVR)和自回归积分滑动平均模型(ARIMA)的组合模型预测网络流量.采用Morlet-SVR和ARIMA分别预测通过Mallat小波分解和单支重构得到的近似信号和多尺度细节信号,最后通过线性叠加得到最终预测结果.通过仿真实验分别对比分析了基于径向基核函数的支持向量机回归算法和ARIMA预测模型,通过3种误差评估得知该组合模型具有更高的预测精度.
2. School of Electronic and Information Engineering, Xi'an Jiaotong University, Xi'an 710049, China;
3. School of Communication and Information Engineering, Xi'an University of Posts and Telecommunications, Xi'an 710061, China
According to the nonlinear and multi-dimensional dynamic characteristics of network traffic, combined with the ability of multi-scale wavelet analysis, a comprehensive forecasting model based on Morlet-support vector regression (Morlet-SVR) and auto regressive integrated moving average (ARIMA) was proposed, in which Morlet-SVR and ARIMA are employed to forecast the approximate signal and the multi-scale detail signals respectively by use of Mallet wavelet decomposition and single reconstruction. The final prediction result is obtained by linear superposition of the layers. Simulations give out comparisons with radial basis function-support vector regression and ARIMA model respectively, the proposed model shows higher prediction accuracy by comparison with three error evaluation measurements.
网络流量预测研究对管理者实时监控网络流量和优化网络部署方案有着重要的意义. 目前关于网络流量预测研究方法主要分为两类:针对线性时间序列的预测和非线性时间序列预测. 线性时间序列预测算法典型的有自回归模型[1]、自回归滑动平均模型(ARMA,auto regressive moving average)[2]、差分自回归滑动平均模型[3]等,这些模型无法高效预测呈非线性特性的网络流量. 针对非线性时间序列的预测,代表算法有分形差分自回归滑动平均模型[4]、基于小波分析的预测模型[5]、基于最大相关熵准则的网络流量预测方法[6]等,这些模型在一定程度上提高了非线性时间序列的预测精度,相比而言算法的复杂度较高. 对于支持向量机回归算法(SVR,support vector regression),其最大的优势在于不仅能够很好地解决非线性和高维度数据集的模型回归问题,而且能够有效地避免维数灾难保证收敛到全局最优点. 文献[7]则通过与反向传播神经网络的对比得出SVR具有更高的预测性能和可扩展性.
笔者结合小波多尺度分析的特性,针对网络流量的非线性和多维度动力学特性,提出基于Morlet小波核函数的支持向量机回归算法(Morlet-SVR,Morlet-support vector regression)和自回归积分滑动平均模型(ARIMA,auto regressive integrated moving average)的组合模型预测网络流量. 通过对网络流量时间序列进行Mallat小波分解和单支重构,生成频率成分更加单一、更加易于预测的时间序列. 对更能反映原始信号趋势的近似信号使用Morlet-SVR进行回归预测,而对不同尺度的细节信号则利用ARIMA进行预测. 仿真实验对比基于径向基核函数的支持向量机回归算法(RBF-SVR,radial basis function-support vector regression)和ARIMA模型对于网络流量的预测,得出该组合模型具有更高的预测精度.
1 预测模型理论 1.1 小波多尺度分析小波变换核心思想是将信号分解到不同的频率上从而实现多尺度分析,它可以通过伸缩平移运算对信号(函数)逐步进行多尺度细化,最终达到高频处时间细分,低频处频率细分,能自动适应时频信号分析的要求,从而可聚焦到信号的任意细节. 小波变换的关键在于选取适当的小波函数和级数,现将网络流量时间序列分解为l层,如式(1)所示.
| $\left. \begin{gathered} s_k^{\left( l \right)} = \sum\limits_n {{h_{{\text{low}}}}\left( {n - 2k} \right)s_n^{l + 1},l \geqslant 0,l \in Z} \hfill \\ d_k^{\left( l \right)} = \sum\limits_n {{h_{{\text{high}}}}\left( {n - 2k} \right)s_n^{l + 1},l \geqslant 0,l \in Z} \hfill \\ \end{gathered} \right\}$ | (1) |
其中:dk为分离所得的细节系数,sk为近似系数,hlow(n)和hhigh(n)分别为低通滤波和高通滤波器的系数,Z为整数集.
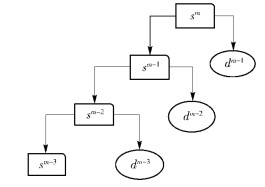
利用小波分解算法,原始信号sm通过小波分解得到低频近似信号sm-j和高频细节信号dm-1,dm-2,…,dm-j,其中j为分解级数. 图 1展示了原始信号sm 3层分解过程. 选用3层小波分解和单支重构来预处理原始流量信号.
1.2 ARIMA算法ARIMA是一种系统模型,它是用于将非平稳时间序列转换为平稳时间序列,然后将因变量仅对其滞后值以及随机误差项的现值和滞后值进行回归所建立的模型. ARIMA模型是由ARMA模型转变而来的,ARMA(p,q)定义为
| ${y_i} = \sum\limits_i^p {{\phi _i}{y_{t - i}} + } \sum\limits_j^p {{\theta _j}{\tau _{t - j}}} $ | (2) |
其中:yt为时间序列,τt为白噪声过程,$\phi $i(i=1,2,…,p)和θj(j=1,2,…,q)均为常量. ARIMA(p,d,q)在ARMA(p,q)的基础上增加了差分操作,进行差分操作的目的是为了将不平稳时间序列转变为平稳时间序列. 具体的ARIMA(p,d,q)模型表示为
| $\begin{gathered} \Delta {x_t} = {\phi _1}\Delta {x_{t - 1}} + {\phi _2}\Delta {x_{t - 2}} + \cdots + {\phi _p}\Delta {x_{t - p}} + \hfill \\ {u_t} - {\theta _1}{u_{t - 1}} - {\theta _2}{u_{t - 2}} - \cdots - {\theta _q}{u_{t - q}} \hfill \\ \end{gathered} $ | (3) |
其中:$\phi $i(i=1,2,…,p)为自回归系数,θi(i=1,2,…,q)为滑动平均系数,Δxt为d阶平稳时间序列,ut为误差项. ARIMA算法以时间序列的自相关分析为基础,对于短期趋势的预测准确率较高,因此可用其预测小波分解所得的细节信号.
1.3 Morlet-SVR算法支持向量机最初用于解决模式识别和其他分类问题,后来扩展到非线性回归和曲线拟合. 算法核心是采用核函数映射,把输入空间的数据映射到一个高维特征空间中去,从而把非线性不可分问题转换为线性可分的问题. 因其高效的曲线拟合能力,笔者采用基于小波核函数的SVR预测通过小波分解所得的近似流量信号.
目前关于SVR的参数求解(包括惩罚系数c、不敏感损失度系数ε和核函数的选择)没有统一标准,只能凭借经验、测试对比、大范围搜索或者交叉验证的方法来寻求最优. 笔者着重从核函数选择方面来改进传统SVR,传统SVR中核函数主要包括线性核函数、多项式核函数、径向基函数和Sigmoid核函数. 下面给出所提出的小波基核函数以及证明其满足Mercer定理.
假定ψ(x)为一维母小波函数,则利用张量积理论,可分离的d维小波函数表示为
| ${\psi _d}\left( x \right) = \prod\limits_{i = 1}^d {\psi \left( {{x_i}} \right)}$ | (4) |
构造平移不变小波核函数:
| $k\left( {x,x'} \right) = k\left( {x,x'} \right) = \prod\limits_{i = 1}^d {\psi \left( {\frac{{{x_i} - {x_i}'}}{{{a_i}}}} \right)} $ | (5) |
其中ai>0为小波伸缩因子. 平移不变核函数应严格满足定理1的条件.
定理1 k(x,x′)=k(x-x′)平移不变核函数是一个允许支持向量核,当且仅当k(x)的傅里叶变换:
| $F\left[{k\left( \omega \right)} \right] = {\left( {2\pi } \right)^{ - 2/d}}\int_{{R^d}} {\exp \left( { - {\text{j}}\omega x} \right)k\left( x \right){\text{d}}x \geqslant 0} $ | (6) |
成立.
在确定具体的小波核函数时,利用某种具体的函数替代母小波即可得到相应的小波核函数. 目前能满足条件的母小波有一维Haar小波、Mexico帽小波、双正交B样条小波和Morlet小波[8]. 笔者选取Morlet小波基函数来代替母小波函数,复Morlet小波[9]的形式为
| $\psi \left( x \right)=\sqrt{\pi {{f}_{\text{b}}}}\exp \left( \text{j2}\pi {{f}_{\text{c}}}x \right)\exp \left( \frac{-{{x}^{2}}}{{{f}_{\text{b}}}} \right)$ | (7) |
其中:fb为频宽,fc为中心频率. 为了构建平移不变小波核函数,取其实部:
| $\psi \left( x \right)=\sqrt{\pi {{f}_{\text{b}}}}\exp \left( \text{2}\pi {{f}_{\text{c}}}x \right)\exp \left( \frac{-{{x}^{2}}}{{{f}_{\text{b}}}} \right)$ | (8) |
则平移不变Morlet小波核函数定义为
| $k\left( x,{x}' \right)=\prod\limits_{i=1}^{d}{\sqrt{\pi {{f}_{\text{b}}}}\cos \left( 2\pi {{f}_{\text{c}}}\frac{{{x}_{i}}-{{x}_{i}}^{\prime }}{a} \right)}\times \exp \left( -\frac{{{\left\| {{x}_{i}}-{{x}_{i}}^{\prime } \right\|}^{2}}}{{{f}_{\text{b}}}{{a}^{2}}} \right)\text{ }$ | (9) |
该平移不变核函数是可允许的支持向量核函数,证明过程见文献[9].
最后本实验所选取量化后的Morlet小波核函数为
| $\begin{gathered} k\left( {x,x'} \right) = \prod\limits_{i = 1}^d {h\left( {\frac{{{x_i} - {x_i}'}}{{{a_i}}}} \right)} = \hfill \\ \prod\limits_{i = 1}^d {\left( {\cos \left( {1.75 \times \frac{{{x_i} - {x_i}'}}{{{a_i}}}} \right)\exp \left( { - \frac{{{{\left\| {{x_i} - {x_i}} \right\|}^2}}}{{2a_i^2}}} \right)} \right)} \hfill \\ \end{gathered} $ | (10) |
其中:d为高维空间的维数,ai为伸缩因子.
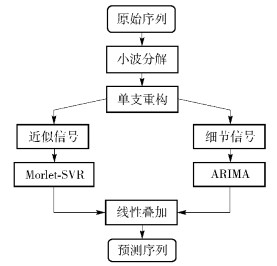
1.4 组合模型网络流量具有明显的分形特征,如自相似性、突变性和长时间依赖性. 因此利用小波变换来分解信号,使得分解所得的信号具有单一的分形特征,然后分别选用Morlet-SVR和ARIMA对分解所得的信号进行预测. 具体的模型如图 2所示.
详细的组合预测模型如下:
1) 对原始信号进行归一化处理得到X.
2) 对原始信号进行小波分解,选取多贝西小波(db1),通过3层分解得到近似信号和各尺度下的细节信号.
3) 对近似信号和细节信号分别进行Mallat单支重构得到a3、d3、d2和d1.
4) 对近似信号a3选取Morlet-SVR进行回归预测. 近似信号在很大程度上能够反映原始序列的整体特征,结合SVR在解决小样本回归的优势和小波基函数在时间和频率两重维度的细化特性,最终利用Morlet-SVR对近似信号进行预测得到A3.
5) 对3层细节信号选取ARIMA进行回归预测. 细节信号着重反映信号的短相关特征,ARIMA能够很好地刻画流量的短相关特性. 最后得到预测信号D3、D2和D1.
6) 对各预测信号进行叠加得到最终的预测信号序列X′.
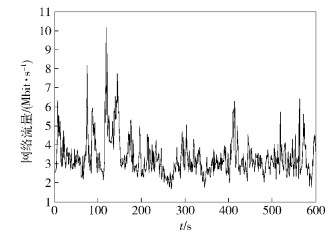
2 仿真实验仿真实验采用真实网络流量数据进行模型预测检验,使用公开流量数据源测试[10],该数据源于怀卡托大学计算机科学系的WAND研究小组,流量采集于奥克兰大学的校园局域网,收集时间段从6:00—12:00. 从中截取600个样本点,采样时间间隔为1 s,如图 3所示. 其中,前550个样本点作为模型构建的训练集,后50个样本点作为检验模型精确度的测试集.
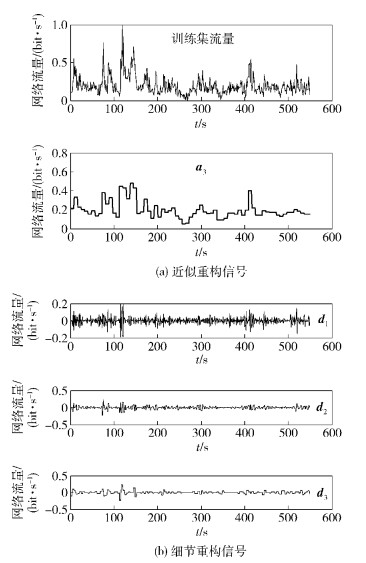
通过归一化得到最终的样本数据. 首先对样本数据进行小波分解与重构. 利用一阶多贝西小波(db1)对样本数据进行3层分解,并进行单支重构,最终得到近似重构信号a3,细节重构信号d3、d2和d1,分别如图 4(a)和图 4(b)所示.
对近似信号,采用Morlet-SVR进行回归预测分析,利用LIBSVM工具箱实现,采用Morlet小波基函数替换传统SVR中的核函数,经实验得到的bestc和bestg分别为11.313 7和0.007 8. 对3层细节信号,选取ARIMA模型进行预测,表 1展示了每层细节信号所对应ARIMA模型的参数.
| 表1 ARIMA(p,d,q)模型参数 |
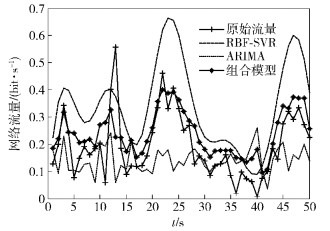
最后对预测所得的信号进行线性叠加得到完整预测值. 为体现组合模型的优越性,分别对比采用RBF-SVR或ARIMA算法的网络流量预测精度. 图 5展示了不同模型回归波形,4条曲线分别代表原始流量、RBF-SVR预测值、ARIMA预测值和组合模型预测值.
出于合理评估预测算法性能的需要,采取3种误差精度表现方法,分别是均方误差(MSE,mean squared error)eMSE、归一化均方误差(NMSE,normalized mean squared error) eNMSE和平均绝对相对误差(MARE,mean absolute relative error) eMARE,如式(11)所示.
| $\left. \begin{gathered} {e_{{\text{MSE}}}} = \frac{1}{N}\sum\limits_{n = 1}^N {{{\left( {X\left( n \right) - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{X} \left( n \right)} \right)}^2}} \hfill \\ {e_{{\text{MSE}}}} = \frac{{\frac{1}{N}\sum\limits_{n = 1}^N {{{\left( {X\left( n \right) - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{X} \left( n \right)} \right)}^2}} }}{{\operatorname{var} \left( {X\left( n \right)} \right)}} \hfill \\ {e_{{\text{MSE}}}} = \frac{1}{N}\sum\limits_{n = 1}^N {\left| {\frac{{X\left( n \right) - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{X} \left( n \right)}}{{X\left( n \right)}}} \right|} \hfill \\ \end{gathered} \right\}$ | (11) |
其中:$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{X} \left( n \right)$为X(n)的预测值,var(X(n))为X(n)的方差,N为时间序列长度.
表 2展示了3种预测算法各自的误差精度,所提出的组合模型要比RBF-SVR或ARIMA模型在时间序列预测方面具有更高的预测精度.
| 表2 预测性能 |
针对网络流量的非线性和多维度动力学特性,结合小波多尺度分析的能力,将原始序列数据通过多贝西小波分解得到反映整体信号趋势的近似信号和多尺度下的细节信号. 针对分解信号的特点采用Morlet-SVR和ARIMA分别预测近似信号和各尺度细节信号,最后通过线性叠加求得最终的预测结果. 仿真实验分别对比RBF-SVR和ARIMA模型,通过MSE、NMSE和MARE 3种误差评估得出所提出的组合模型具有更高的预测精度. 未来的研究点是拓展应用对象到更高维数据样本,另外可以结合类似神经网络这类机器学习理论,探索出一种更为高精度的预测模型.
| [1] | Chen Bor-sen, Peng Sen-chueh, Wang Ku-chen. Traffic modeling, prediction, and congestion control for high-speed networks:a fuzzy AR approach[J]. IEEE Transactions on Fuzzy Systems, 2000, 8(5):491-508.[引用本文:1] |
| [2] | 邹柏贤, 刘强. 基于ARMA模型的网络流量预测[J]. 计算机研究与发展, 2002, 39(12):1645-1652. Zou Boxian, Liu Qiang. ARMA-based traffic prediction and overload detection of network[J]. Journal of Computer Research and Development, 2002, 39(12):1645-1652.[引用本文:1] |
| [3] | Wang Jin. A process level network traffic prediction algorithm based on ARIMA model in smart substation[C]//IEEE Signal Processing, Communication and Computing (ICSPCC). Kunming:IEEE, 2013:1-5.[引用本文:1] |
| [4] | 陈晓天, 刘静娴. 改进的基于小波变换和FARIMA模型的网络流量预测算法[J]. 通信学报, 2011, 32(4):153-157. Chen Xiaotian, Liu Jingxian. Network traffic prediction based on wavelet transformation and FARIMA[J]. Journal on Communications, 2011, 32(4):153-157.[引用本文:1] |
| [5] | Zhang Kun, Chai Yinping, Fu Xing-an. A network traffic prediction model based on recurrent wavelet neural network[C]//IEEE Computer Science and Network Technology (ICCSNT). Changchun:IEEE, 2012:1630-1633.[引用本文:1] |
| [6] | Qu Hua, Ma Wentao, Zhao Jihong, et al. Prediction method for network traffic based on maximum correntropy criterion[J]. China Communications, 2013, 10(1):134-145.[引用本文:1] |
| [7] | Wei Xianmin. Supporting vector-machine prediction of network traffic[C]//IEEE Electrical and Control Engineering (ICECE). Yichang:IEEE, 2011:3203-3206.[引用本文:1] |
| [8] | 李元诚, 方廷健. 小波支持向量机[J]. 模式识别与人工智能, 2004, 17(2):167-172. Li Yuancheng, Fang Tingjian. Wavelet support vector machines[J]. Pattern Recognition and Artificial Intelligence, 2004, 17(2):167-172.[引用本文:1] |
| [9] | 陈维荣, 郑永康, 戴朝华, 等. 基于复Morlet小波SVM的负荷预测[J]. 西南交通大学学报, 2009, 44(5):631-636. Chen Weirong, Zheng Yongkang, Dai Chaohua, et al. Short-term load forecasting based on complex Morlet wavelet SVM[J]. Journal of Southwest Jiaotong University, 2009, 44(5):631-636.[引用本文:2] |
| [10] | Waikato. Waikato Internet traffic storage(WITS)[EB/OL]. Waikato:Wand Network Research Group(2011)[2011].http://wand.net.nz/wits/waikato/8/20110520-000000-0.php.[引用本文:1] |