2. 国家计算机网络应急技术处理协调中心, 北京 100029
在对未知应用静态分析的基础上,提取AndroidManifest.xml中申请的权限为特征,采用信息增益算法优化选择分类特征,再采用拉普拉斯校准、乘数取自然对数改进的朴素贝叶斯算法创建恶意应用分类器.通过十折交叉试验验证改进的朴素贝叶斯分类器的准度和精度较高,且通过信息增益优化选择的分类特征在保障准确率的情况下能有效提高检测效率.与k最近邻和k-Means分类器相比,改进的朴素贝叶斯分类器具有较好的分类效果.
2. National Computer Network Emergency Response Technical Team/Coordination Center of China(CNCERT/CC), Beijing 100029, China
Permissions are extracted as features via static analysis. The information gain (IG) algorithm is applied to select significant features. The Naïve Bayesian (NB) classifier is created which is improved through Laplace calibration and natural logarithm of multiplier. The results with 10-fold cross validation indicate that the improved NB classifier achieves higher accuracy and precision, and the selected features by IG algorithm improve the detection efficiency in ensuring the accuracy of the case. Comparing k-nearest neighbor (KNN) and k-Means classifier, NB classifier has good performance on validity, accuracy and efficiency.
Android平台的恶意程序制作成本逐渐降低,且可批量生成恶意程序,致使针对移动端的攻击行为逐渐规模化.据360互联网安全中心统计,2015年全年累计截获Android平台新增恶意程序样本326.0万个,平均每天恶意程序感染量达到了87.5万人次.经研究发现,资费消耗、隐私获取和恶意扣费类型的计算机应用程序(APP,application)所占比例超过90%.另外,还暗藏恶意传播、诱骗欺诈、系统破坏、远程控制等非法行为,给用户带来巨大损失[1].
笔者提出对Android应用逆向工程提取Permission信息为特征;采用信息增益(IG,information gain)算法对特征优化选择,提高运算效率;采用以Laplace校准、乘数取自然对数方式改进朴素贝叶斯(NB,Nave Bayesian)算法,建立分类器,识别恶意应用;最后给出试验对比结果和分析.
1 NB算法 1.1 算法内涵NB分类算法对于准备好的训练数据集,首先基于特征条件独立假设学习输入/输出的联合概率分布;然后基于此模型,对特定的输入X,利用贝叶斯定理求出后验概率最大的输出Y[2, 3].
1)设输入空间为n维向量的集合,输出空间为类标记集合{c1,c2,…,ck},X为定义在输入空间上的随机变量,Y为定义在输出空间上的随机变量.
2)训练数据集
| $T=\left\{ {\left({{x_1},{y_1}} \right),\left({{x_2},{y_2}} \right),\cdots,\left({{x_n},{y_n}} \right)} \right\}$ | (1) |
其中:xn为第n个样本,yn为第n个样本的类别.
3)NB算法的条件概率分布假设为条件独立假设.
| $P\left({X=x\left| {Y={c_k}} \right.} \right)=\prod\limits_{j=i}^n {p\left({{x^{\left(i \right)}}={x^{\left(i \right)}}\left| {Y={c_k}} \right.} \right)} $ | (2) |
其中:x(i)为样本的第i个特征,xn(i)为第n个样本的第i个特征.
4)先验概率为P(Y=ck),通过学习模型计算后验概率分布为
| $\begin{array}{l} P\left({Y={c_k}\left| {X=x} \right.} \right)=\\ \frac{{P\left({X=x\left| {Y={c_k}} \right.} \right)P\left({Y={c_k}} \right)}}{{\sum\limits_k {P\left({X=x\left| {Y={c_k}} \right.} \right)P\left({Y={c_k}} \right)} }} \end{array}$ | (3) |
将式(2)代入式(3)得
| $\begin{array}{l} P\left({Y={c_k}\left| {X=x} \right.} \right)=\\ \frac{{P\left({Y={c_k}} \right)\prod\limits_{j=i}^n {p\left({{x^{\left(i \right)}}={x^{\left(i \right)}}\left| {Y={c_k}} \right.} \right)} }}{{\sum\limits_k {P\left({Y={c_k}} \right)\prod\limits_{j=i}^n {p\left({{x^{\left(i \right)}}={x^{\left(i \right)}}\left| {Y={c_k}} \right.} \right)} } }} \end{array}$ | (4) |
5)NB分类器为
| $y=\arg \;\mathop {\max }\limits_{{c_k}} \frac{{p\left({Y={c_k}} \right)\prod\limits_{j=i}^n {p\left({{x^{\left(i \right)}}={x^{\left(i \right)}}\left| {Y={c_k}} \right.} \right)} }}{{\sum\limits_k {p\left({Y={c_k}} \right)\prod\limits_{j=i}^n {p\left({{x^{\left(i \right)}}={x^{\left(i \right)}}\left| {Y={c_k}} \right.} \right)} } }}$ | (5) |
式(5)中的分母对所有ck都是相同的,则
| $y=\arg \;\mathop {\max }\limits_{{c_k}} \prod\limits_{j=i}^n {p\left({{x^{\left(i \right)}}={x^{\left(i \right)}}\left| {Y={c_k}} \right.} \right)} $ | (6) |
对于NB分类器的评价指标采用准确率、受试者工作特征(ROC,receiver operating characteristic)曲线和ROC曲线下的面积(AUC,area under curve)[4].
准确率反映分类器的正确判定能力,即将正类判定为正类,负类判定为负类,定义为(TP+FN)/(TP+TN+FP+FN).其中:真正(TP,true positive),真负(TN,true negative),假正(FP,false positive),假负(FN,false negative).
ROC曲线反映分类器的优劣,以假正率(FPR,false positive rate)为横轴,真正率(TPR,true positive rate)为纵轴,描绘分类器的灵敏度,曲线越接近左上角,说明该分类器性能越好.
AUC值越大,说明分类效果越好.在ROC曲线无法清晰反映分类效果时,比较AUC的值,有助于增强分类器之间的比对.
2 NB算法改进基本的NB算法对数据处理不够细致,容易产生偏差,笔者对此提出2点改进措施.
1)Laplace校准
在NB算法分类时,需要计算多个概率的乘积,以得到属于某个应用类别的概率,即计算式(5)的值,如果其中一个条件概率为0,总的结果也为0,会影响整个分类结果,解决这一问题的关键是采用Laplace校准[3],即为每个类别所有特征划分的计数都加1,为了避免下溢出时的乘数太小,为每个类别样本的计数加2,样本集数量足够大,不会对结果产生影响,还解决了概率为0的问题.
2)自然对数避免下溢出
由于太多很小的数相乘会造成下溢出,或不正确,采取对乘积取自然对数的解决方法,将连乘变为连加.另外,在运算效率上,加法也比乘法降低了分类的时间复杂度O(n).采用自然对数可避免下溢出或浮点数舍入导致的错误,且不会有任何损失.
经Laplace校准和乘数取自然对数改进的NB分类器为
| $\begin{array}{l} y=\arg \;\mathop {\max }\limits_{{c_k}} \sum\limits_{j=i}^n {\;\ln p\left({\left({{x^{\left(i \right)}}={x^{\left(i \right)}}\left| {Y={c_k}} \right.} \right)} \right)}=\\ \arg \;\mathop {\max }\limits_{{c_k}} \sum\limits_{j=i}^n {\ln \left({\frac{{\sum\limits_{i=1}^N {I\left({x_i^{\left(j \right)}={a_j},{y_i}={c_k}} \right)+1} }}{{\sum\limits_{i=1}^N {I\left({{y_i}={c_k}} \right)+2} }}} \right)} \end{array}$ | (7) |
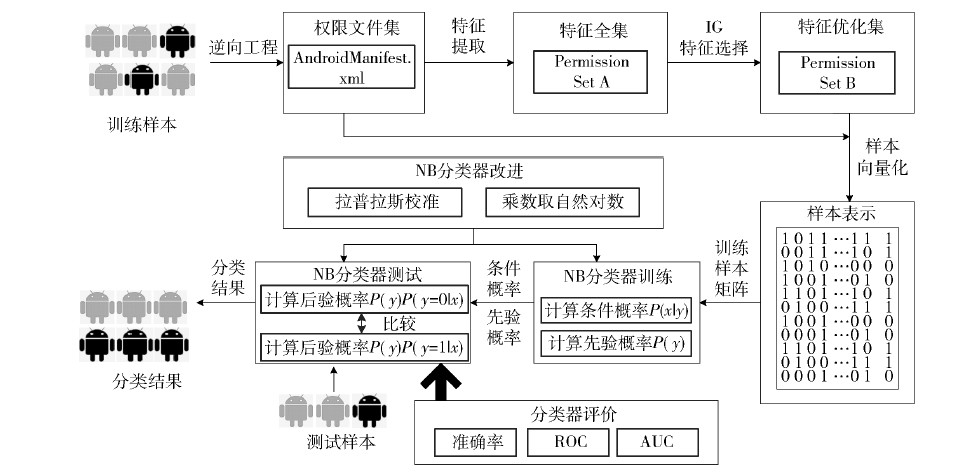
以Permission为特征属性[5],采用改进的NB算法为分类器,快速地识别出恶意应用,具体的应用分类模型如图 1所示.
分类模型分为3个阶段,第1阶段为数据准备阶段.首先,对训练样本Android安装包(APK,Android package)进行反编译,提取AndroidManifest.xml中的权限作为分类特征,对各样本的特征集合求并集A,作为分类的特征全集;采用IG特征选择算法,优化提取区分度明显的特征优化集B,作为分类器的输入.分类效果很大程度上取决于样本本身的质量和特征选取的质量,这一阶段的效果对整个分类过程起到决定性作用.
第2阶段为分类器训练阶段,主要任务是计算训练样本中的条件概率和先验概率,它们对分类器的测试效果起到决定性影响.通过调节样本集中的样本分布,可得较好效果的条件概率和先验概率.
第3阶段为分类器测试阶段,主要任务是对测试样本进行分类,并对分类器效果进行评价.按照十折交叉验证,将样本集轮流地以9:1的比例划分为训练集和测试集,根据改进的NB分类原理,计算每个测试样本在类别划分中的概率和每个特征在每个类别的条件概率,经过Laplace校准、对乘数取自然对数,得到其趋向于各个类别的概率,进一步得到应用的分类类别,与真实类别相比较,使用准确率和AUC对分类器的分类效果进行评价.
4 试验与测试 4.1 试验样本在测试过程中共采集了3 644个样本,其中1 844个是良性应用,分别下载自广受信赖的应用商城Google Play,包含所有应用类别.另外1 800个应用为恶意应用,从https://virusshare.com、http://sanddroid.xjtu.edu.cn网站上收集,覆盖恶意应用家族的所有类别.
4.2 样本分析对于上述采集到的应用样本,通过静态分析方式,使用AXMLPrinter2、Dex2jar、JD-GUI等工具逆向APK应用文件,提取出权限信息作为应用的特征.
在对应用样本集实际分析的过程中,经过统计发现,无论是良性应用还是恶意应用,最经常申请的权限为INTERNET、READ_PHONE_STATE、ACCESS_NETWORK_STATE和WRITE_EXTERNAL_STORAGE,它们也是应用内置广告推送的必要权限,是由现阶段应用的商业模式决定的.较多的恶意应用申请如SEND_SMS、RECEIVE_SMS、READ_SMS和WRITE_SMS等短信相关的权限,可能导致泄露隐私或资费消耗等风险.
4.3 特征选择采用IG特征选择算法[6],计算各特征在分类器中的信息增益,值越大,说明该特征对分类越重要.其中,排在前20种的权限如表 1所示.
| 表1 IG算法优化选择的前20种特征 |
在IG选择的分类特征中,包含这些特征的恶意应用数目大于良性应用.经统计,约69%的恶意应用申请了短信相关权限,约6%的良性应用申请了短信相关权限,且较多恶意应用申请了RECEIVE_BOOT_COMPLETED、GET_TASKS、READ_PHONE_STATE和CHANGE_WIFI_STATE等权限,这表明恶意应用存在隐私泄露、资费消耗、远程控制等风险.
4.4 改进的NB分类器在测试过程中,基于十折交叉验证原则,轮流将样本集的90%作为训练集,10%作为测试集,取10次试验的平均结果,作为对分类器精度的估计.
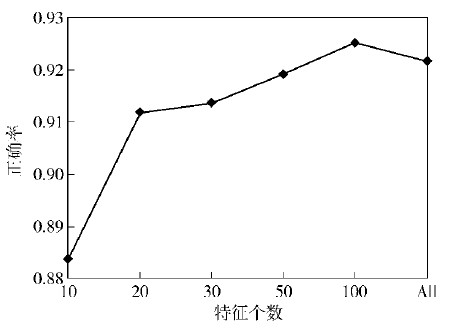
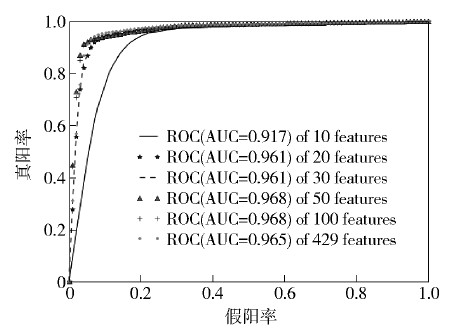
试验针对3 644个样本,通过IG算法,选择信息增益值较大的前10、20、30、50、100种和全部特征作为分类器输入,结果取平均值,统计结果如图 2和图 3所示.
分析上述试验结果,可得以下结论:
1)改进的NB分类器对恶意应用检测有很大作用,准确率高达90%以上;
2)随着特征数目的增加,准确率和AUC随之增加,当特征数目增加到一定程度后,准确率变化不明显,说明经IG算法选择出的少量特征能代表整个样本的特征,且能排除冗余和噪声特征对分类效果的干扰;
3)结合分类器的工作时间,在追求准确率的情况下,可增加特征数目,在追求效率的情况下,平衡准确率,可减少分类器输入的特征数目.
4.5 不同分类器比较常用的有监督分类器有NB、k最近邻(KNN,k-nearest neighbor)、支持向量机(SVM,support vector machine)、决策树(DT,decision tree)、逻辑斯谛回归(LR,logistic regression)等[7],无监督分类器有k-Means等,其中NB为最简单的分类器,直接对应用分类,分类效率较高;其他有监督分类器都经历复杂的训练过程,影响了分类效率;而无监督分类器分类准确率和效率较低.笔者在使用中对NB、KNN和k-Means分类器的比较如表 2所示.
| 表2 不同分类器准确率和AUC比较 |
比较结果表明,在相同的样本特征情况下,改进的NB分类器优于KNN和k-Means分类器.在Android应用分类的场景下,综合考虑分类效率和分类效果,建议采用改进的NB分类器.
5 结束语分析良性应用和恶意应用的特点,提取Permission为属性特征,并采用IG特征选择算法优化提取特征,再采用改进的NB算法建立基于权限的Android恶意应用分类器,智能化地识别恶意应用.
对NB分类器的改进体现在Laplace校准和对乘数取自然对数,主要目的是为了解决乘数为0和太多较小乘数相乘的问题,避免在分类器计算过程中产生结果偏差,进而提高算法的精度.
在十折交叉试验过程中,当特征数目超过20种时,改进的NB分类器准确率达到90%以上.然而,由于现在的很多恶意应用刻意伪装成良性应用,在特征表现上很相似,为恶意应用的正确识别带来很大困难.未来可结合应用程序编程接口(API,application programming interface)调用序列,选择更有区分度的特征,提高分类器的准度和精度.
| [1] | Zhou Yajin, Jiang Xuxuan. Dissecting android malware:characterization and evolution[C]//Security and Privacy(SP), 2012 IEEE Symposium on. San Francisco:IEEE, 2012:95-109.[引用本文:1] |
| [2] | Mitchell T. Machine learning[M]. Beijing:China Machine Press, 2012:112-136.[引用本文:1] |
| [3] | Harrington P. Machine learning in action[M]. New York:Manning Publications Co Development, 2013:62-82.[引用本文:1] |
| [4] | Davis J, Goadrich M. The relationship between precision-recall and ROC curves[C]// Proceedings of the 23rd International Conference on Machine Learning.New York:ACM, 2006:233-240.[引用本文:1] |
| [5] | Felt A P, Chin E, Hanna S, et al. Android permissions demystified[C]//Proceedings of the 18th ACM Conference on Computer and Communications Security. New York:ACM, 2011:627-638.[引用本文:1] |
| [6] | Feizollah A, Anuar N B, Salleh R, et al. A review on feature selection in mobile malware detection[J]. Digital Investigation, 2015, 13:22-37.[引用本文:1] |
| [7] | Cen Lei, Gates C S, Si Luo, et al. A probabilistic discriminative model for android malware detection with decompiled source code[J]. Dependable and Secure Computing, IEEE Transactions on, 2015, 12(4):400-412.[引用本文:1] |