2. 解放军96518部队, 怀化 418000;
3. 解放军信息工程大学, 郑州 450001
在非平衡基下,通过局域操作引入纠缠态的非对称性,证明了非平衡基可以提高连续变量量子密码方案的密钥生成速率.以典型的密钥分配实验为例,经过数值计算验证,在同等密钥生成速率的条件下,非平衡基的量子密钥分配安全距离可以扩展20 km左右.
2. PLA 96518 Division, Huaihua 418000, China;
3. PLA Information Engineering University, Zhengzhou 450001, China
With its security based on quantum no-cloning and Heisenberg uncertainty relation, the quantum cryptography is a newly developed key distribution protocol. The recent research on continuous variable quantum cryptography assumes that the choice of basis is balanced. However, the performance of continuous variable quantum cryptography is an interesting but open question. By introducing the asymmetry in the shared bipartite two-mode entanglement state, the secret key rate was improved with unbalanced basis. Furthermore, numerical simulations with typical continuous variable quantum key distribution experiment show that the secure distance can be prolonged by 20km for a given secure key rate.
量子密码又称量子密钥分配,是20世纪80年代信息领域兴起的一项新兴技术[1].连续变量量子密码采用光子的正则动量和正则坐标进行编码,在解码时光探测效率可以接近100%[2].现有的关于连续变量量子密码的研究都是建立在Alice和Bob两组基的选择是完全平衡的条件下进行的.非平衡选基对于连续变量量子密码的影响是一个有趣而公开的问题.
笔者研究非平衡基条件下连续变量量子密码方案,通过在Alice和Bob之间共享的纠缠态上引入局域操作的办法,提高了量子密码方案的密钥生成率,获得比平衡基条件下更远的密钥分发距离.
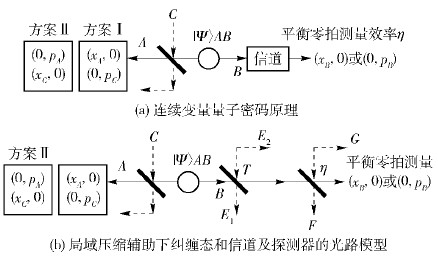
1 连续变量量子密码方案 1.1 基于非平衡基的连续变量量子密码协议首先给出基于两模纠缠态的非平衡基连续变量量子密码协议[3].
1)Alice制备两模纠缠态$\hat{S}\left(s \right)\otimes \hat{S}\left(s \right){{\left| \psi \right\rangle }_{AB}}$,并将B模式通过量子信道发送给Bob.
2)Bob分别以p0和1-p0的概率采取平衡零拍测量的方法测量(xB,0)或(0,pB).
3)Alice采用外差法测量手中的A模式量子态:将A模式与真空C模式利用50:50的光学分束器进行耦合.而后Alice采取两种备选方案.第Ⅰ种方案,Alice分别在A模式和C模式测量(xA,0)和(0,pC);第Ⅱ种方案,Alice分别在A模式和C模式测量(0,pA)和(xC,0);在非平衡基密码协议中,Alice的这两种测量方案的概率不相等,分别为p0和1-p0.
4)Bob通过经典信道与Alice进行比对,二者仅保留同时测量正交位置分量或同时测量正交动量分量的测量结果.
5)Alice和Bob交换部分数据,并判断通信是否安全.若安全,二者通过密钥纠错和保密增强技术最终获取保密且完全一致的密钥.否则,放弃.
图 1(a)展示了实际情形下的连续变量量子密钥分配方案.A-B为两模纠缠态,B模式被送到一个透过效率为T、热噪声为ε的信道.而后在Bob端采用一个探测效率为η的探测设备进行探测.其中,非平衡基指方案Ⅰ与方案Ⅱ的选取概率不相等.
1.2 协议的安全性分析模型对原理图 1(a)的联合攻击可以用图 1(b)所示的联合攻击模型加以表示.不失一般性,假设信道是由参数T和ε共同决定的热噪声信道.在光路上,一般用一个透过率为T和一个纯的两模压缩真空态|ψ〉E1E2表示.而非理想探测效率的平衡零拍探测器则由一个透过率为η和一个额外辅助的纯两模压缩真空态|ψ〉GF表示.|ψ〉E1E2和|ψ〉GF的方差分别是VE1E2=1+Tε/(1-T),VGF=1+vel/(1-η),其中ε和vel分别为热噪声水平和平衡零拍探测器的电子噪声水平[4].
在Alice和Bob分别进行零拍测量之后,二者的测量结果会形成一定的关联.这种关联进而形成了二者之间共有的保密密钥.在非平衡基条件下且Alice采取方案Ⅰ和方案Ⅱ的概率各为p0和1-p0时,总体的密钥生成率可以表示为
| $R=p_{0}^{2}{{R}^{\left(x \right)}}+{{\left(1-{{p}_{0}} \right)}^{2}}{{R}^{\left(p \right)}}$ | (1) |
其中R(x)=βIAB(x)-χBE(x)、R(p)=βIAB(p)-χBE(p)分别表示在正则坐标方向和正则动量方向上形成的密钥生成率,IAB(x)(IAB(p))为Alice和Bob测量结果之间的互信息,χBE(x)(χBE(p))为窃听者的量子态与Bob测量结果之间的量子Holevo信息[5].0<β<1指Alice和Bob进行反向数据调谐的效率.
2 非对称基下的密钥生成率计算 2.1 正则位置方向在图 1(b)的光路中,量子信道为高斯信道,平衡零拍测量为高斯测量,Alice和Bob的测量结果都服从高斯分布,二者互信息IAB(x)可以由测量结果的方差给出$I_{AB}^{\left(x \right)}=\frac{1}{2}\text{lb}\frac{{{V}_{B}}}{{{V}_{\left.B \right|A}}}$,其中VB为Bob测量结果的方差,而VB|A为Alice公布自己的测量结果之后Bob测量结果的条件概率分布所对应的方差.VB和VB|A的计算需要借助于图 1(b)中量子态的演化.首先,需要引入两模压缩真空态的协方差矩阵
| $\gamma \left(V \right)=\frac{1}{2}\left(V{{I}_{4}}+\sqrt{{{V}^{2}}-1}\left(\begin{matrix} {} &1 \\ 1 &{} \\ \end{matrix} \right)\otimes \left(\begin{matrix} 1 &{} \\ {} &-1 \\ \end{matrix} \right)\right)$ |
光路中的透过率为T的分束器则可以表示为对于协方差的辛变换.具体地,作用在k和l两个模式上透过率为t的分束器可以表示为$S_{^{BS}}^{\left( k,l \right)}=\sqrt{t}{{I}_{4}}+\sqrt{1-t}\left( \begin{matrix} 1 & {} \\ {} & -1 \\ \end{matrix} \right)\otimes {{I}_{2}}$.于是,A、B、C、E1、E2、F、G这7个模式的量子态演化可以表示为
| ${\Gamma _{AB{E_1}{E_2}FG}} = {S_{{\rm{tot}}}}\left[ {{\gamma _{AB}} \oplus \frac{1}{2}{I_2}^{\left( c \right)} \oplus \gamma \left( {{V_{{E_1}{E_2}}}} \right) \oplus \gamma \left( {{V_{FG}}} \right)} \right]S_{{\rm{tot}}}^{\rm{T}}$ | (2) |
其中Stot=SBSBF(η)SBSBE1(T)SBSAC(1/2),γAB=[S(s)⊕S(s)]γ(V)[S(s)⊕S(s)]T,S(s)=diag(es,e-s)为单模压缩操作的辛变换.
所关心的Bob测量结果的方差则可以由ΓABE1E2FG的B模式的量子态的x分量所给出.经过计算,可以得出VB(x)=N0ηT(Ve2s+χtot),χtot=χline+χhom /T,χline=1/T-1+ε,χhom =(1+vel)/η-1.VB|A(x)的值则反映了Bob已知Alice测量结果的条件下Bob手中的测量结果的不确定度.由于本小节着重研究正则坐标方向形成的密钥,于是Alice将采取方案Ⅰ进行测量.根据平衡零拍测量的基本理论,可以得到VB|A(x)=Tη(1+χtot)/2+Tη(e2s-e-2s)/(2e-2s+2V).以下考查窃听者和Bob测量结果之间的Holevo信息量.根据Holevo信息量[6]定义,
| $\chi _{BE}^{\left(x \right)}=S\left({{\rho }_{{{E}_{1}}{{E}_{2}}}} \right)-\int{\text{d}{{x}_{B}}p\left({{x}_{B}} \right)}Sp\left(\rho _{{{E}_{1}}{{E}_{2}}}^{{{x}_{B}}} \right)$ | (3) |
其中:ρE1E2为Bob探测之前的五模量子态ABCE1E2中两模E1E2的约化密度矩阵,ρxBE1E2为Bob测量结果为xB时五模纯态AE1E2FG的E1E2约化密度矩阵,S(·)为冯诺伊曼熵[7].由于ρE1E2为高斯态,有$S\left({{\rho }_{{{E}_{1}}{{E}_{2}}}} \right)=\sum\limits_{i=1}^{2}{G\left({{\beta }_{i}}-\frac{1}{2} \right)}$,${{\beta }_{1}}=\sqrt{\frac{1}{2}A-\sqrt{{{A}^{2}}-4B}}$,${{\beta }_{2}}=\sqrt{\frac{1}{2}A+\sqrt{{{A}^{2}}-4B}}$,A=(V2(1-T)2+T2χline2+2T+(e-2s+e2s)T2Vχline)/4,B=T2(e2s+Vχline)(e-2s+Vχline)/16.在Bob进行完平衡零拍测量并且测量得到结果为xB后,五模态AE1E2FG仍然是纯态.B模进行的x方向平衡零拍测量等价于将ABE1E2FG六模态的B模投影到一个一阶量为(xB,0)、协方差阵为diag(e-2ξ,e2ξ)且ξ→∞的高斯态.AE1E2FG五模态的协方差阵为$V_{{{E}_{1}}{{E}_{2}}AFG}^{xB}={{\gamma }_{{{E}_{1}}{{E}_{2}}AFG}}-{{\sigma }_{{{E}_{1}}{{E}_{2}}AFG,B}}\left(\begin{matrix} 1/\gamma _{B}^{\left(1,1 \right)} &0 \\ 0 &0 \\ \end{matrix} \right)\sigma _{{{E}_{1}}{{E}_{2}}AFG,B}^{\text{T}}$把经过所有分束器之后的六模态的协方差矩阵进行分块,并重排:
| ${{V}_{{{E}_{1}}{{E}_{2}}FGB}}=\left(\begin{matrix} {{\gamma }_{{{E}_{1}}{{E}_{2}}AFG}} &{{\sigma }_{{{E}_{1}}{{E}_{2}}AFG,B}} \\ \sigma _{{{E}_{1}}{{E}_{2}}AFG,B}^{\text{T}} &{{\gamma }_{B}} \\ \end{matrix} \right)$ |
其中γB(1,1)为γB矩阵的第1行第1列元素.ρE1E2xB的协方差矩阵可以由VE1E2AFGB左上4×4子矩阵给出.因此,有$S\left(\rho _{_{{{E}_{1}}{{E}_{2}}}}^{{{x}_{B}}} \right)=\sum\limits_{i=1}^{2}{G\left({{\lambda }_{i}}-\frac{1}{2} \right)}$,其中${{\lambda }_{1}}=\sqrt{\frac{1}{2}\left(C-\sqrt{{{C}^{2}}-4D} \right)}$,${{\lambda }_{2}}=\sqrt{\frac{1}{2}\left(C+\sqrt{{{C}^{2}}-4D} \right)}$, $\begin{align} & C=\frac{TV\left({{\text{e}}^{2s}}+V{{\chi }_{\text{line}}} \right)+T\left({{\text{e}}^{2s}}V+{{\chi }_{\text{line}}} \right)+4A{{\chi }_{\text{hom}}}}{4T\left({{\text{e}}^{2s}}V+{{\chi }_{\text{tot}}} \right)} \\ & D=\frac{TV\left({{\text{e}}^{2s}}+V{{\chi }_{\text{line}}} \right)+16B{{\chi }_{\text{hom}}}}{16T\left({{\text{e}}^{2s}}V+{{\chi }_{\text{tot}}} \right)} \end{align}$ S(ρE1E2xB)是与xB数值无关的量,因而
| ${{R}^{\left(x \right)}}=I_{AB}^{\left(x \right)}-\sum\limits_{i=1}^{2}{G\left({{\beta }_{i}}-\frac{1}{2} \right)+}\sum\limits_{i=1}^{2}{G\left({{\lambda }_{i}}-\frac{1}{2} \right)}$ |
在正则动量方向,Alice将采取方案Ⅱ进行测量,Bob也将在正则动量方向获取数据.相应的$V_{{{E}_{1}}{{E}_{2}}AFG}^{pB}={{\gamma }_{{{E}_{1}}{{E}_{2}}AFG}}-{{\sigma }_{{{E}_{1}}{{E}_{2}}AFG,B}}\left(\begin{matrix} 0 &0 \\ 0 &1/\gamma _{B}^{\left(2,2 \right)} \\ \end{matrix} \right)\sigma _{{{E}_{1}}{{E}_{2}}AFG,B}^{\text{T}}$密钥生成率可以表示为
| ${{R}^{\left(p \right)}}=I_{AB}^{\left(p \right)}-\sum\limits_{i=1}^{2}{G\left(\beta _{i}^{'}-\frac{1}{2} \right)+}\sum\limits_{i=1}^{2}{G\left(\lambda _{i}^{'}-\frac{1}{2} \right)}$ |
其他相关的参数为
| $\begin{align} &V_{B}^{\left(p \right)}=\eta T\left(V{{e}^{-2s}}+{{\chi }_{\text{tot}}} \right)/2 \\ &V_{\left.B \right|A}^{\left(p \right)}=T\eta \left(1+{{\chi }_{\text{tot}}} \right)/2+T\eta \left({{e}^{-2s}}-{{e}^{2s}} \right)/\left(2{{e}^{2s}}+2V \right)\\ &{{A}^{'}}=\left({{V}^{2}}{{\left(1-T \right)}^{2}}+{{T}^{2}}\chi _{\text{line}}^{2}+2T+\left({{e}^{-2s}}-{{e}^{2s}} \right){{T}^{2}}V{{\chi }_{\text{line}}} \right)/4 \\ &{{B}^{'}}=N_{0}^{4}{{T}^{2}}\left({{e}^{2s}}+V{{\chi }_{\text{line}}} \right)\left({{e}^{-2s}}+V{{\chi }_{\text{line}}} \right)/16 \\ &{{C}^{'}}=\frac{TV\left({{e}^{-2s}}+V{{\chi }_{\text{line}}} \right)+T\left({{e}^{-2s}}V+{{\chi }_{\text{line}}} \right)+4{{A}^{'}}{{\chi }_{\hom }}}{4T\left({{e}^{-2s}}V+{{\chi }_{\text{tot}}} \right)} \\ &{{D}^{'}}=\frac{TV\left({{e}^{-2s}}+V{{\chi }_{\text{line}}} \right)+16{{B}^{'}}{{\chi }_{\hom }}}{16T\left({{e}^{-2s}}V+{{\chi }_{\text{tot}}} \right)} \end{align}$ |
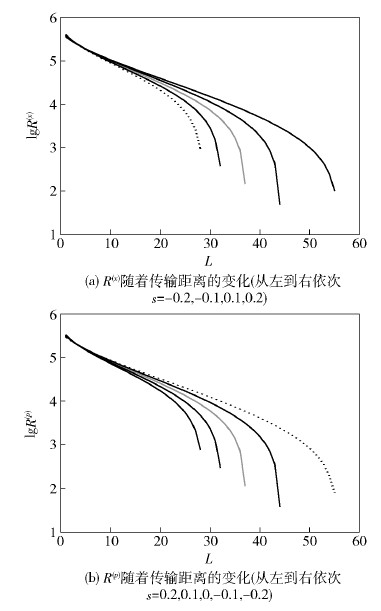
以上分别从正则位置方向和正则动量方向获得了密钥生成率.当s=0即无压缩时,容易得出R(x)=R(p)并且与文献[4]一样.
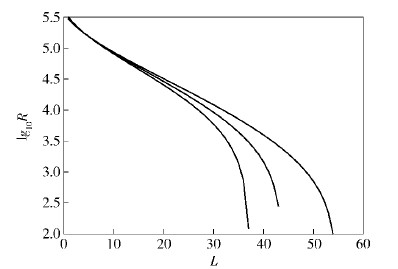
3 典型参数下的密钥生成速率选取方差V=19.5,探测效率η=0.606,电子学噪声vel=0.041,并设信道采用1 550 nm的光纤通信信道,光纤损耗为0.20 dB/km,系统重复频率为350 kHz,图 2给出了R(x)和R(p)随着传输距离的变化关系.当s=0时R(x)=R(p),而不断地增大s,修正后的两模纠缠态在正则坐标方向和正则动量方向上的方差进行了分化.所形成的密钥量也随即变化.随着s的增大,R(x)增加而R(p)减小.若s取负值并且|s|增大时则有R(x)减小而R(p)增加.图 3中选取了p0=0.1并给出了整体的密钥生成率R随着传输距离的变化关系.局域操作?(s)的引入在密钥生成率方面可以带来较大的改善.以s=0.1为例,密钥在L=58 km处仍然有较大的生成速率.而无压缩即s=0时密钥在L=38 km处即趋向于零.因此,局域压缩在密钥分配的距离上有较大的扩展.
4 讨论
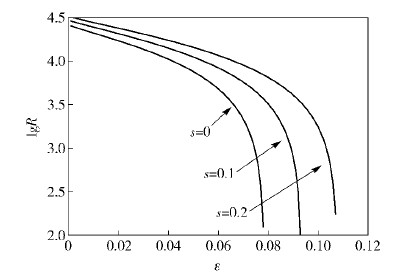
密钥生成率的提高给实际连续变量量子密码系统带来了诸多好处,它可以提高系统抗干扰能力.以信道热噪声为例,ε的增大,使得量子密钥分配形成的数据关联度降低,形成的密钥数目下降.以20 km的通信距离为例,比较了s=0和s=0.2时密钥生成率与ε的依赖关系.如图 4所示,在局域压缩存在下,密钥生成率对ε=0.078的容忍度可以提高到ε=0.107,这给连续变量量子密码系统设计带来便利.
5 结束语证明了非平衡基在连续变量量子密码中的优势,同时,通过局域压缩操作证实了在密钥生成率方面,局域压缩修正的纠缠态可以保证更远的安全距离.从纠缠态的角度为进一步改进连续变量量子密码协议提供了一种思路.
| [1] | Bennett C H, Brassard G. Quantum cryptography:public key distribution and coin tossing[C]//Processing of the IEEE International Conference on Computers, Systems, and Signal Processing. Bangalore:IEEE Press, 1984:175-179.[引用本文:1] |
| [2] | Hillery M. Quantum cryptography with squeezed states[J]. Physical Review A, 2000, 61:022309(1)-022309(8).[引用本文:1] |
| [3] | Grosshans F, Grangier P. Continuous variable quantum cryptography using coherent states[J]. Physical Review Letters, 2000, 88:057902(1)-057902(4).[引用本文:1] |
| [4] | Lodewyck J, Bloch M, García-Patrón G, et al. Quantum key distribution over 25 km with an all-fiber continuous-variable system[J]. Physical Review A, 2007, 76:042305(1)-042305(10).[引用本文:2] |
| [5] | Holevo A S, Sohma M, Hirota O. Capacity of quantum Gaussian channels[J]. Physical Review A, 1999, 59:1820-1828.[引用本文:1] |
| [6] | Pirandola S, Ottaviani C, Spedalieri G, et al. High-rate measurement-device-independent quantum cryptography[J]. Nature Photonics, 2015, 9:397-402.[引用本文:1] |
| [7] | Von Neumann J. Mathematische grundlagen der quantenmechanik[M]. Berlin:Springer, 1932.[引用本文:1] |