2. 西安邮电大学通信与信息工程学院, 西安 710061
提出了一种蜂窝网络中关于移动中继的选择方案,将小区内的用户按照下行路径损耗分为一跳用户和两跳用户.一跳用户由基站直接对其分配资源,两跳用户采用整体优化的吞吐量预测中继选择算法选择空闲用户作为中继节点.该算法全面考虑了带宽与信道质量对通信速率的影响,以两跳用户所在接入链路与回程链路吞吐量相等为原则主动调节两跳用户带宽分配比例,并且通过匈牙利算法计算出系统吞吐量最大时的最佳匹配矩阵.仿真结果表明,该算法能够有效提升边缘用户吞吐量和频谱利用率.
2. The School of Telecommunication and Information Engineering, Xi'an University of Posts and Telecommunications, Xi'an 71006 l, China
A mobile relay selection scheme used in the cellular network was designed, it divides the users into one-hop users and two-hop ones according to the path loss. The one-hop users receive signal from the Base Station (BS) directly. However, the two-hop users could choose the idle one-hop users as Relay Nodes (RN) with the global optimal throughput prediction relaying (GOTPR). The proposed algorithm puts the impact of bandwidth and channel quality onto the rate of communication into account adequately, adjusts the bandwidth of two-hop users based on the equality of throughput of access link and backhaul link, and acquires the optimal matching matrix with the maximum throughput by the Hungarian algorithm. Simulations presents that the proposed method could improve the cell edge users throughput and spectral efficiency significantly.
多跳蜂窝网络中信道质量好的移动节点(MNs,mobile nodes)与基站(BS,base station)直接进行通信,边缘用户选择信道质量好的用户作为中继节点(RN,relay node)与基站进行间接通信[1],从而在覆盖范围、传输速率以及通信能耗方面都得到有效提升[2, 3].为了更好地分配宽带资源,提出了一种基于吞吐量预测的整体优化中继选择算法(GOTPR,global optimal throughput prediction relaying).两跳用户通过采用GOTPR算法,平衡了接入链路(AL,access link)与回程链路(BL,backhaul link)的吞吐量并且利用匈牙利算法为两跳用户匹配更合理的中继,从而有效提升两跳用户吞吐量和频谱利用率.
1 研究背景传统选择算法中,对中继节点的选取问题提出了多种算法.机会中继策略(OR,opportunistic relaying)是应用最为广泛的一种.其核心思想是,以信道质量为指标,选出所有备选中继节点实时链路信干噪比最大的节点作为最优中继[4].另外,一些文章直接以到用户的距离作为参考因素,选择两跳用户通信范围内,离基站最近的用户作为中继节点[5].其中,OR算法首先选择两跳用户所在接入链路与回程链路中信干噪比较小的链路作为“瓶颈链路”.然后,将两跳用户通信范围内的空闲用户纳入备选中继集合,选出其中“瓶颈链路”信干噪比最大时所对应的空闲用户作为最优中继,能够提升边缘用户吞吐量,但由于只能被动地选取相对较好的用户,因此对通信速率的提升相当有限.另外,Hossain等[5]所提方法,具有算法复杂度低的优势,但是该方法没有考虑两条链路中的瓶颈效应,具有一定的盲目性,对通信质量的提升不明显.为此,提出了GOTPR算法,考虑了带宽资源与信道质量对传输速率的影响,加入了吞吐量预测环节,以两跳用户所在接入链路与回程链路吞吐量相等为原则调节带宽分配比例,接着建立指派问题的数学模型,通过匈牙利算法得出系统吞吐量最大时的最佳匹配矩阵[6].如此,可以变被动选择为主动调节,能有效提升边缘用户平均吞吐量以及频谱利用率.所提算法以蜂窝小区场景为例进行阐述,但应用场景并不局限于蜂窝小区.
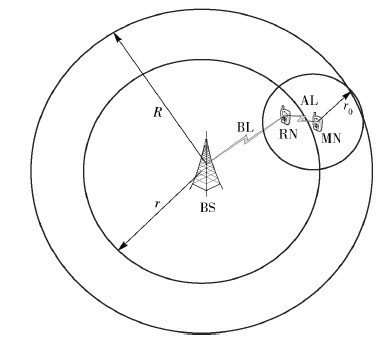
2 GOTPR算法模型 2.1 用户区分策略蜂窝小区按照通信距离远近被分为中心区域与边缘区域,如图 1所示.其中,中心区域内的用户与基站直接通信,称为一跳用户;边缘区域内的用户通过中心区域用户与基站进行通信,称为两跳用户[1].
图 1中,R为小区半径,r为中心小区半径,r0为用户通信范围,其中中心小区半径r由用户通信范围r0与小区半径R共同决定,即r=R-r0.基于文献[5]和[7],小区半径R=1 000 m,用户通信范围r0=200 m,中心小区半径r=800 m.
基站收到资源请求后,向用户发送参考信号,然后基站根据式(1)计算下行路径传播损耗值L:
| $L=58.83+37.6\lg D+211{\rm{g}}f$ | (1) |
其中:D为基站与用户的距离,f为中继蜂窝系统的载频(一般取2 GHz),基站将每个用户的下行路径传播损耗值与下行路损判决门限Lth进行比较,Lth取图 1中中心区域与边缘区域交界线上用户到基站之间的路径损耗,若L<Lth,则用户为一跳用户;若L≥Lth,则用户为两跳用户.
2.2 资源初始分配基站根据一跳用户与两跳用户所占的比例进行带宽资源的初始分配,当用户随机分布时可按照中心区域与边缘区域面积之比初始分配带宽资源.假设,基站包含资源块总数为Stotal,分配给一跳用户的资源块数目为S1,分配给两跳用户的资源块数目为S2.则,S1与S2满足如下关系:
| $=\left.\begin{array}{l} {S_1}+{S_2}={S_{{\rm{total}}}}\\ \frac{{{S_1}}}{{{S_2}}}=\frac{{\pi {r^2}}}{{\pi {R^2}+\pi {r^2}}} \end{array} \right\}$ | (2) |
提出的GOTPR算法将接入链路与回程链路的带宽分配比例设定为可变值,通过调节分配比例使得两条链路用户吞吐量相等,进而有效规避了“瓶颈效应”造成的资源浪费.GOTPR算法的核心思想是,两跳用户向周围用户发送参考信号,将周围所有空闲用户,总数为N,纳入备选中继集合,基站将备选中继集合内所有用户所在的接入链路与回程链路分配资源的比例设为可变值,然后以两条链路吞吐量相等为原则,计算出两条链路带宽资源分配值的大小,并通过匈牙利算法求得使系统吞吐量最大时的最佳匹配矩阵,接着利用最佳匹配矩阵对每个用户分配合适的中继节点.
基于GOTPR算法的实现满足如下规则:
规则1:
| ${S_{{\rm{AL}}}}+{S_{{\rm{BL}}}}=\frac{{{S_2}}}{{{N_{{\rm{user}}}}}}$ | (3) |
其中:S2为系统预留给两跳用户的资源块总数,Nuser为系统接入的两跳用户总数,SAL与SBL分别为两跳用户接入链路与回程链路理论上分得的资源块数目.即认为每个两跳用户获得带宽资源的概率均等,且为其所在两条链路分得资源之和.
规则2:
| ${C_{{\rm{AL}}}}=B{S_{{\rm{AL}}}}{\rm{lb}}\left({1+{\gamma _{{\rm{AL}}}}} \right)$ | (4) |
| ${C_{{\rm{BL}}}}=B{S_{{\rm{BL}}}}{\rm{lb}}\left({1+{\gamma _{{\rm{BL}}}}} \right)$ | (5) |
| ${C_{{\rm{AL}}}}={C_{{\rm{BL}}}}$ | (6) |
其中:CAL为接入链路的吞吐量预测值,SAL为接入链路分配的资源块数目预测值,γAL为接入链路的信干噪比;CBL为回程链路吞吐量预测值,SBL为回程链路分得的资源块数目预测值,γBL为回程链路的信干噪比;B为单个资源块所占的带宽.式(4)和(5)按照香农定理预测出两跳用户所在链路的吞吐量,其中S2、Nuser和B为已知参数,γAL和γBL可以在基站端测试得到,SAL、SBL、CAL和CBL是未知参数,联立公式(3)、(4)、(5)、(6)可以求出SAL与SBL.
规则3:
| $\begin{array}{l} \;\;\;\;\;\;\;\;{P_{ij}}=\max \left\{ {{Q_{ij}}} \right\} - {Q_{ij}}\\ i=1,2,\cdots,M;j=1,2,\cdots,N \end{array}$ | (7) |
式(7)中,效益因子Qij是指第i个用户被第j个用户协助所产生的吞吐量预测值,即规则2中求得的CAL与CBL.其中,两跳用户的总数是M个,所有两跳用户通信范围内的可能被选作中继的用户总数是N个.由于匈牙利算法需要求出效益因子之和的最小值,因此将效益因子Qij转化为新的效益因子Pij.一般情况下,两跳用户数目M总是小于备选中继数目N,因此要将非平衡指派问题转化为指派问题,需要借助于“虚设变量”,将原效益矩阵P增加N-M行,得方阵${{P}^{'}}={{\left[ \frac{{{P}_{M\times N}}}{{{0}_{\left( N-M \right)\times N}}} \right]}_{N\times N}}$.需要注意的是,增加的0元素是没有意义的,并不会对指派问题的求解结果产生影响.为每一个两跳用户/中继用户定义一个二值函数Xij:
| ${x_{ij}}=\left\{ \begin{array}{l} 1\;\;\;\;\;第i个两跳用户选择第j个中继\\ 0\;\;\;\;\;第i个两跳用户未选择第j个中继 \end{array} \right.$ |
则指派问题的数学模型为
| $z=\min \sum\limits_{i=1}^{N}{\sum\limits_{j=1}^{N}{P_{ij}^{'}}}{{X}_{ij}}$ | (8) |
| $\sum\limits_{i=1}^N {{X_{ij}}=1\;\;\;j=1,2,\cdots,N} $ | (9) |
| $\sum\limits_{j=1}^N {{X_{ij}}=1\;\;\;j=1,2,\cdots,N}$ | (10) |
| ${X_{ij}}=1,0$ | (11) |
由P′ij组成的矩阵P′=(P′ij)N×N称为指派问题效率矩阵,则式(8)~(11)解的问题等价于:
从P′中选择n个元素,使满足:1)每列中恰有一个元素被选中,以保证每个中继用户只协助一个两跳用户通信;2)每行中恰有一个元素被选中,以保证一个两跳用户只借助于一个中继用户进行通信;3)被选出的n个元素和最小.
由于指派问题具有这样的性质,从系数矩阵P′的一行(列)各元素中分别减去该行(列)的最小元素得出的新矩阵求出的最优解与原矩阵所求最优解相同,利用这一性质并结合匈牙利算法,在变形的系数矩阵中找出N个独立的0元素,这便是系统吞吐量最大时的最佳匹配矩阵,接着按照最佳匹配矩阵对两跳用户分配合适的中继节点,并且按照SAL和SBL对合适的中继的两条链路分配资源块.
3 仿真结果分析本节中将建立移动中继节点选择模型,并利用该模型对所提算法以及传统算法进行仿真分析.在仿真中,对比了中继场景下经典的机会中继算法、选择距离基站最近用户算法以及提出的GOTPR算法.
模拟郊区环境中的蜂窝小区环境进行对GOTRP算法进行仿真[7].系统资源块总数100块,基站发射功率PBS=40 W,中继用户发射功率PMN=40 W,基站天线增益GBS=15 dBi,中继用户天线增益GMN=5 dBi.对于选择距离基站最近用户算法和OR算法,当多个边缘用户选中同一中继时,产生最大吞吐量的边缘用户被选中.利用上述参数对GOTPR算法进行了仿真,从边缘用户平均吞吐量和频谱利用率方面与传统中继节点选择算法进行了对比并且仿真了匈牙利算法解决中继选择冲突次数.
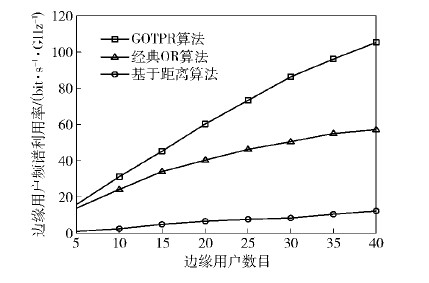
图 2为3种选择算法的小区边缘用户频谱利用率对比图.其中,选择用户通信范围内离基站最近用户作为中继的算法在选择中继节点时,没有考虑链路的信道质量,具有一定的盲目性以至于对系统性能的提升并不明显;经典的机会中继算法即OR算法,在选择中继节点时,考虑了接入链路与回程链路信道质量的对比,选择出通信质量最好的链路进行信号传输,能有效提升边缘用户的频谱利用率;所提出的GOTPR算法,通过调节接入链路与回程链路分配的带宽资源,避免了“瓶颈效应”造成的资源浪费,并且通过匈牙利算法实现了边缘用户与中继用户的最佳匹配选择,与经典OR算法相比明显提升了边缘用户频谱利用率.由此说明所提算法确实有效地提高了边缘用户频谱利用率.
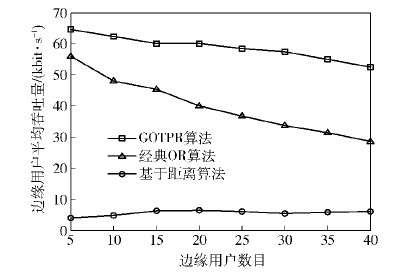
图 3为3种选择算法的小区边缘用户平均吞吐量对比图.其中,GOTPR算法与经典OR算法相比依然明显提升了边缘用户的平均吞吐量,而且随着边缘用户数目增加,对于基于距离算法来说,由于其中继选择具有一定的盲目性,因此边缘用户数目增多对于其平均吞吐量的影响并不大.而与经典OR算法相比,GOTPR算法下的边缘用户平均吞吐量下降慢,这是因为随着边缘用户数目增多,每个边缘用户的备选中继集合之间会产生更多的选择冲突,由于GOTPR算法采用了匈牙利算法选取最佳匹配矩阵,因此能够有效缓解选择冲突导致的边缘用户平均吞吐量下降.
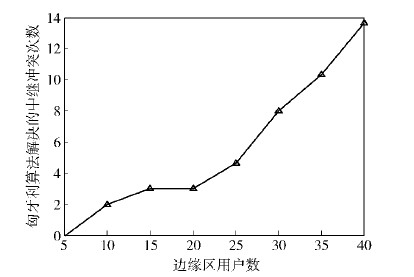
图 4中选择冲突次数随着边缘用户数目的增加而增加,因为当多个边缘用户选中同一用户作为备选中继节点时,若只是简单按照此边缘用户吞吐量大小作为这一中继支持哪个边缘用户的准则,那么对于整个小区来说按照这一准则所求吞吐量并不是最大的.然而当采用匈牙利算法时,求出了边缘用户与备选中继的最佳匹配矩阵,按这一准则将会产生最大的系统吞吐量,而且当边缘用户增多时,多个边缘用户选中同一备选中继而产生冲突可能性大大增加,而GOTPR算法可以有效解决这一问题.因此,GOTPR算法更适用于边缘用户数目较多的情况.
4 结束语为了提升蜂窝小区边缘用户吞吐量及系统频谱利用率等性能,提出了一种基于吞吐量预测的整体优化中继节点选择策略(GOTPR).该策略中,根据用户到基站的路径损耗,将用户分为一跳用户和边缘两跳用户,系统按照两跳用户接入链路与回程链路吞吐量相等给两条链路分配带宽资源,接着利用匈牙利算法求出最佳匹配矩阵,对每个两跳用户选择合适的中继分配预先估算好的带宽.将所提算法与传统的经典算法进行对比,通过仿真实验,验证了所提中继节点选择算法方法对边缘用户吞吐量与频谱利用率等方面的性能有明显提升,对整个系统的性能也有很大改善.
| [1] | Lin Y D, Hsu Y C. Multihop cellular:a new architecture for wireless communications[C]//INFOCOM. Tel Aviv:IEEE, 2000:1273-1282.[引用本文:2] |
| [2] | Sendonaris A, Erkip E, Aazhang B. User cooperation diversity:Part I. System description[J]. IEEE Transactions on Communications, 2003, 51(11):1927-1938.[引用本文:1] |
| [3] | 唐菁敏, 罗涛, 乐光新. 基于中继选择的认知系统性能[J]. 北京邮电大学学报, 2011, 3(3):44-47. Tang Jingmin, Luo Tao, Yue Guangxin. Performance of cognitive system based on relay selection[J]. Journal of Beijing University of Posts and Telecommunications, 2011, 3(3):44-47.[引用本文:1] |
| [4] | Bletsas A, Khisti A, Reed D P, et al. A simple cooperative diversity method based on network path selection[J]. IEEE Journal on Selected Areas in Communications, 2006, 24(3):659-672.[引用本文:1] |
| [5] | Hossain M F M, Mämmelä A, Chowdhury H. Impact of mobile relays on throughput and delays in multi-hop cellular network[C]//ICWMC. Athens:IEEE, 2008:304-308.[引用本文:3] |
| [6] | 柳毅, 佟明安. 匈牙利算法在多目标分配中的应用[J]. 火力与指挥控制, 2002, 27(4):34-37. Liu Yi, Tong Mingan. An application of Hungarian algorithm to the multi-target assignment[J]. Fire Control & Command Control, 2002, 27(4):34-37.[引用本文:1] |
| [7] | Zhang Hao, Hong Peilin, Xue Kaiping. Mobile-based relay selection schemes for multi-hop cellular networks[J]. Journal of Communications & Networks, 2013, 15(1):45-53.[引用本文:2] |