传统协同过滤方法面临数据稀疏问题,稀疏的用户-项目关联数据将产生不准确的相似用户或项目,为了改善推荐质量,提出一种基于Map Reduce的混合协同过滤方法.该方法利用用户特征和用户-项目评分数据构造项目偏好向量,然后使用模糊K-Means算法对项目进行聚类,并从每个项目簇中选择相似项目,最后组合所有项目簇的预测结果作出推荐.实验结果显示,该方法能缓解数据稀疏问题,改善推荐精度.
Addressing the information overloading problem, the collaborative filtering is an effective technique, and extensively applied in recommender systems. It make predictions by finding users with similar taste or items that have been similarly chosen. However, as the number of users or items grows rapidly, the traditional collaborative filtering approach is suffering from the data sparsity problem. The sparse user-item associations can generate inaccurate neighborhood for each user or item. A distributed hybrid collaborative filtering method was proposed based on Map Reduce, aiming at improving the recommendation quality. This method utilizes user features and ratings to construct item preference vectors. Then, it clusters items using fuzzy K-Means algorithm, and respectively chooses similar items from each clustering, finally it combines all predictions from each clustering and makes recommendation. Experiments show that the distributed hybrid collaborative filtering method can help reduce the sparsity problem, and improve the recommendation accuracy.
当前不断增加的数据量使用户需要花费很多时间才能找到自己喜欢的项目.协同过滤(CF,collaborative filtering)是解决这一问题的有效技术之一,并已应用于一些网站.但CF是依赖用户对项目的共同评分来计算相似性的,因此共同评分的稀疏性将影响相似性度量的精度和推荐质量.
为解决上述问题,笔者提出了一种基于Map Reduce的分布式混合协同过滤(DHCF,distributed hybrid collaborative filtering)方法.该方法在个性化推荐中利用用户特征信息和用户-项目评分矩阵构造项目偏好向量.用户特征的引入有助于检测用户和项目之间的隐含关系,缓解数据稀疏性,而这种关系正是传统CF所缺失的.该方法首先使用模糊K-Means算法依据项目特征和项目偏好将项目聚类到不同的簇中,然后在各个项目簇中为目标项目选择相似项目集,最后汇合各簇的计算结果作出推荐.
1 相关研究传统CF利用用户对项目的共同评分来计算用户的相似度.为有效利用单评分,Xu等[1]提出将单评分转为共同评分的方法.Zhang等[2]使用项目领域特征来构建用户偏好模型,并将此用户偏好模型与CF相结合.Yang[3]提出使用条件概率分布来捕获社交网络中朋友之间的相似性.上述方法通常依赖于用户的各种反馈,但每个人的描述习惯和语言表达方式具有多样性,因此影响了利用反馈信息或社交系统信息计算用户相似性的准确性.
为解决多样性和模糊性问题,Boulkrinat等[4]采用定性评价方法来表达不精确和模糊的用户偏好.Son[5]提出了一种混合式基于用户的模糊协同过滤(HU-FCF,hybrid user-based fuzzy collaborative filtering)方法.在HU-FCF方法中,用户之间的最终相似度集成了模糊相似度和硬相似度,前者根据人口统计数据计算获得,后者依据用户的历史评分计算得到.
在实现技术方面,Xu等[1]和Xie等[6]采用Map Reduce实现对数据的并行处理,Apache的Mahout开源项目亦使用Map Reduce实现传统的CF(Mahout CF).
2 DHCF方法DHCF包括3个阶段:①构建项目的偏好向量;②利用项目偏好和项目基本特征对项目进行模糊聚类;③基于项目簇的CF.
2.1 构建项目的偏好向量经济学和心理学理论建议将一个异质市场细分为较小的同质消费群体,使得每个消费者群中成员有类似的需求、特性或行为.在推荐系统中,为分析项目在各类用户群中的影响,DHCF借鉴市场细分原理先将用户细分为若干类用户,再生成每类用户对于各项目的偏好,然后将项目偏好加入到项目轮廓中.
项目轮廓包含两大类项目特征:基本特征和项目偏好.基本特征用于描述项目的基本特性,如电影流派;项目偏好用于描述项目受各类用户群欢迎的程度.DHCF利用各类用户群中用户对项目的历史评分构建项目偏好向量.假设Rm×n为m个用户和n个项目的评分矩阵,其中ru,i∈Rm×n是用户u对项目i的评分.Uj是用户j的特征向量.C={S1,S2,…,St}是利用模糊K-Means算法对用户聚类而得到的用户簇集.由于采用的是模糊聚类,所以每个用户Uj按一定概率pj,l指派给多个用户簇,其中pj,l为Uj隶属于用户簇Sl∈C的概率.Ei=(ej,li)表示用户簇中用户对项目i的评分矩阵,其中矩阵行为m个用户,列为t个用户簇,ej,li为第l用户簇中用户j对项目i的评分(由式(1)定义).
| $e_{j,l}^i = \left\{ \begin{array}{l} {r_{j,i}},\;\;j \in {S_l}\\ 0,\;\;\;\;j \notin {S_l} \end{array} \right.$ | (1) |
用V={vi,1,vi,2,…,vi,t}描述项目偏好特征向量,其中vi,l(1≤l≤t)为项目i对用户簇l的偏好特征(由式(2)定义).
| ${v_{i,l}} = \frac{{\sum\limits_{^{^{{w_{i,l}}}}j \in \left\{ {j\left| {e_{j,l}^i > 0,j \in {S_l},{S_l} \in C} \right.} \right\}} {\left( {{P_{j,l}}e_{j,l}^i} \right)} }}{{\sum\limits_{j \in \left\{ {j\left| {e_{j,l}^i > 0,j \in {S_l},{S_l} \in C} \right.} \right\}} {{P_{j,l}}} }}$ | (2) |
其中wi,l为偏好特征的权重,表示为
| ${w_{i,l}} = \frac{{\left| {\left\{ {j\left| {e_{j,l}^i > 0,j \in {S_l},{S_l} \in C} \right.} \right\}} \right|}}{{\mathop {\max }\limits_{1 \le h \le t} \left\{ {\left| {\left\{ {j\left| {e_{j,h}^i > 0,j \in {S_h},{S_h} \in C} \right.} \right\}} \right|} \right\}}}$ |
用Ii=(bi,1,…,bi,q,vi,1,…,vi,t)表示项目i的特征向量,其前q列为项目的基本特征值,后t列为项目偏好值.
2.2 项目的模糊聚类CF算法的一个重要步骤是搜索目标的邻居集.为了缩小搜索范围,DHCF利用模糊K-Means聚类方法为每个项目簇选取隶属概率大于阈值θ的项目,生成K个项目簇B={G1,G2,…,GK}.同时,为每个项目簇G∈B分配唯一的簇标识ZG.由于项目聚类将所有项目划分为若干较小的项目簇,因此便于采用分而治之的方法,在Map Reduce计算环境中对各个项目簇进行并行处理.
2.3 基于项目簇的CF在推荐系统中,Pearson相关系数可用于度量两个评分向量之间的线性相关性.但若两个评分向量的共同评分太少,则将影响相似度的正确性.为了克服这个问题,DHCF在计算项目相似度Sim(i1,i2)时采用式(3)综合项目评分相似度和项目特征相似度.
| $\begin{array}{l} Sim\left( {{i_1},{i_2}} \right) = \frac{{\omega Sim\left( {{i_1},{i_2}} \right)Q\left( {{i_1},{i_2}} \right)}}{{\mathop {\max \left( {\left\{ {Q\left( {i,j} \right)} \right\}} \right)}\limits_{i,j \in G} }} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {1 - \omega } \right)Si{m_{\rm{F}}}\left( {{i_1},{i_2}} \right) \end{array}$ | (3) |
其中:i1,i2∈G,G∈B;Q(i1,i2)表示同时对项目i1和i2评分的用户数;ω为项目评分相似度SimR(i1,i2)的权值;SimF(i1,i2)为项目特征相似度,由式(4)中的欧氏距离定义.
| $\begin{array}{l} D\left( {{I_{i1}},{I_{i2}}} \right) = \sqrt {\sum\limits_{j = 1}^q {{{\left( {{b_{{i_1},j}} - {b_{{i_2},j}}} \right)}^2}} } + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sqrt {\sum\limits_{j = 1}^t {{{\left( {{v_{{i_1},j}} - {v_{{i_2},j}}} \right)}^2}} } \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;Si{m_{\rm{F}}}\left( {{i_1},{i_2}} \right) = \frac{1}{{1 + D\left( {{I_{i1}},{I_{i2}}} \right)}} \end{array}$ | (4) |
模糊K-Means允许将项目i指派给多个项目簇,因此当预测用户u对项目i的评分时,可能会跨越多个项目簇,预测评分步骤如下.
1) 分别在每个项目簇G∈B中搜索项目i的邻居集NG(i)={j|Sim(i,j)≥d,i,j∈G},d为邻居相似度阈值.
2) 剔除重复的邻居.由于任意一个项目和其部分邻居均可能被指派到多个项目簇中,所以在各项目簇中搜索到的项目邻居集的交集可能不为空,即满足条件$\mathop \cap \limits_{G \in B} {N_G}\left(i \right)\ne \emptyset$.为避免在预测评分时某个邻居多次参与预测,需要从NG(i)中剔除重复的邻居.
3) 分别在项目簇G∈B中按照式(5)计算用户u对项目i邻居项的评分加权偏差和、相似度和.
| $\left. \begin{array}{l} {e_G}\left( {u,i} \right) = \sum\limits_{h \in {N_G}\left( i \right)} {\left( {{r_{u,h}} - {A_h}} \right){\mathop{\rm sim}\nolimits} \left( {i,h} \right)} \\ {S_G}\left( {u,i} \right) = \left| {\sum\limits_{h \in {N_G}\left( i \right)} {{\mathop{\rm sim}\nolimits} \left( {i,h} \right)} } \right| \end{array} \right\}$ | (5) |
其中Ah为用户对项目h的平均评分.
4)汇总各项目簇的处理结果,按照式(6)计算预测评分.
| ${P_{u,i}} + {A_i} + \frac{{\sum\limits_{_{G \in B}} {{e_G}\left( {u,i} \right)} }}{{\sum\limits_{_{G \in B}} {{S_G}\left( {u,i} \right)} }}$ | (6) |
其中Ai为用户对项目i的平均评分.
3 基于Map Reduce的DHCF实现基于Map Reduce的DHCF实现包含3大步骤:①采用Apache Mahout项目提供的模糊K-Means算法构建项目的偏好向量;②对项目进行模糊聚类;③按照2.3节介绍的原理实现基于项目簇的CF,该步骤包含2对Map-Reduce(MR)作业.
第1对MR作业定义了3类映射器:评分数据映射器、项目映射器和预测目标映射器.预测目标映射器读取目标用户和项目对(ua,ib),获取项目ib所隶属的项目簇ZG,然后输出键值对〈ZG,(ua,ib)〉.评分数据映射器读取评分数据文件的用户u对项目i的评分(u,i,ru,i),然后依据第2步的项目模糊聚类结果,获取项目i所隶属的项目簇标识ZG,生成并输出键值对〈ZG,(u,i,ru,i)〉,其中ZG为关键字,(u,i,ru,i)为值.项目映射器读取项目i的特征向量Ii,在获取项目i所隶属的项目簇标识ZG之后,生成并输出键值对〈ZG,Ii〉.
各映射器所在节点以并行方式将上述输入数据依据ZG分别映射到该簇对应的预测目标集TG、项目特征向量集IG和评分矩阵RG中,然后再依据关键字将上述集合中相同键值的值合并,合并后键值对记为L=〈ZG,TG∪RG∪IG〉.这些经排序和组合后的键值对将被派发给第1对MR作业中Reduce组件,并按如下过程处理.
1) 读入键值对L,解析获得关键字ZG,然后再从值列表中解析获得隶属于ZG簇的TG、RG和IG.
2) 采用Pearson相关系数公式计算RG中各项目之间的评分相似度;依据式(4)计算IG集中各项目之间项目特征相似度;依据式(3)计算项目之间的相似度.
3) 针对TG中每个目标ib,进行如下过程处理.
OG=Ø; For(∀ib∈TG)在IG中搜索项目ib的邻居集NG(ib);
从NG(ib)中剔除重复的邻居;
计算RG中各用户对ib的平均分Aib;
For(∀(ua,ib)∈TG)
利用式(5)计算eG(ua,ib)和SG(ua,ib);
v=(ua,Aib,eG(ua,ib),SG(ua,ib));
OG=OG∪{v};
key=(ib,ZG);
输出键值对〈key,OG〉;
End for
End For第2对MR作业的Map组件读取上一对MR的输出,并输出键值对〈key,OG〉;然后Map端将相同键值的值合并到一个集合中,并派发给Reduce组件处理.Reduce读取合并后的键值对,并解析得到ib在各个簇中的预测结果,然后使用式(6)预测目标(ua,ib)的评分.
4 实验及结果分析为比较各算法的推荐质量,采用Java语言分别实现了DHCF、HU-FCF方法[5]和基于项目的协同过滤(ICF,item-based collaborative filtering)算法.HUFCF和ICF均使用Pearson相关系数测量项目之间的评分相似度,并使用式(7)预测评分.为了确保公平性,对这些算法的参数进行了优化,以达到各自最佳性能.
| ${P_{u,i}} + {A_i} + \frac{{\sum\limits_{h \in {N_i}} {\left( {{r_{u,h}} - {A_h}} \right){\mathop{\rm sim}\nolimits} \left( {i,h} \right)} }}{{\sum\limits_{h \in {N_i}} {\left| {{\mathop{\rm sim}\nolimits} \left( {i,h} \right)} \right|} }}$ | (7) |
其中Ni为项目i的邻居集.
实验采用平均绝对误差(M)、召回率(W)和准确率(H)评估算法的精度.平均绝对误差是预测评分和真正评分之间误差的平均值;召回率指推荐命中总数占测试集中所有相关项的比例;准确率也称为命中率,是推荐命中总数占推荐列表长度的比例.通常情况下,准确率和召回率并不是孤立讨论的,常采用F1度量,实验采用式(8)计算F1.
| ${F_1} = \frac{{2WH}}{{\left( {W + H} \right)}}$ | (8) |
实验搭建的Hadoop平台拥有7台物理计算机.采用3个数据集:MovieLens 100 KB、MovieLens 1 MB以及Yahoo! Movies.前2个数据集用户数分别为943和6 040,项目数分别为1 680和3 900;第3个数据集用户数为1 699,项目数为1 167.
4.1 节点数对算法执行速度的影响表 1显示了分别使用MovieLens 1 MB和100 KB数据集在Hadoop上运行DHCF和Mahout CF实现所需要的执行时间.结果显示:与K/2个Reduce节点数相比,当DHCF采用K个Reduce节点数处理Reduce任务时,由于对K个项目簇的计算分布在K个节点上并行运行,所以DHCF运行时间可明显缩短.表 1也显示了DHCF算法执行时间快于Mahout CF实现.
| 表1 在MovieLens上的执行时间 |
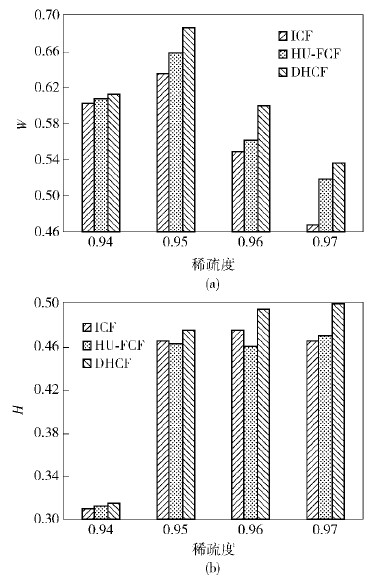
图 1显示DHCF的召回率和准确率在MovieLens 100KB数据集上均优于另外2种算法.特别是数据集稀疏时改善更为显著.例如,当稀疏度为0.94和0.97时,DHCF的召回率相对于ICF分别提高了1.9%和12.9%,相对于HU-FCF分别提高了0.8%和3.5%;DHCF的准确率相对于ICF分别提高了1.3%和6.9%,相对于HU-FCF分别提高了1.2%和5.5%.
4.3 评分相似度权重影响为确定可产生最佳推荐精度的评分相似度权重ω,实验尝试了不同ω值.表 2比较了在不同ω值下使用Yahoo!数据集的预测质量,Top-N设置为10,项目模糊聚类数K=1.实验结果表明,当数据集变得稀疏时,ω取值将变小,如在稀疏度为0.99,ω为0.9时,DHCF可达到最佳F1和M值.
| 表2 ω对推荐质量的影响 |
为缓解数据集的稀疏性,DHCF方法在项目轮廓中引入项目偏好,利用已有的评分数据和用户特征生成项目偏好向量.利用模糊聚类方法将项目分为若干簇,然后采用Map Reduce范式实现对各簇中项目相似度计算、邻居选择和推荐的并行计算处理.
| [1] | Xu Ruzhi, Wang Shuaiqiang, Zheng Xuwei, et al. Distributed collaborative filtering with singular ratings for large scale recommendation[J]. The Journal of Systems and Software, 2014, 95(9):231-241.[引用本文:2] |
| [2] | Zhang Jing, Peng Qinke, Sun Shiquan, et al. Collaborative filtering recommendation algorithm based on user preference derived from item domain features[J]. Physica A:Statistical Mechanics and Its Applications, 2014, 396(2):66-76.[引用本文:1] |
| [3] | Yang Xiwang, Guo Yang, Liu Yong. Bayesian-inference based recommendation in online social networks[J]. IEEE Transactions on Parallel and Distributed Systems, 2013, 24(4):642-651.[引用本文:1] |
| [4] | Boulkrinat S, Hadjali A, Mokhtari A. Towards recommender systems based on a fuzzy preference aggregation[C]//Proceeding of the Eighth Conference of the European Society for Fuzzy Logic and Technology (EUSFLAT-13). Milan:[s. n.], 2013:146-153.[引用本文:1] |
| [5] | Son L H. HU-FCF:a hybrid user-based fuzzy collaborative filtering method in recommender systems[J]. Expert Systems with Applications, 2014, 41(15):6861-6870.[引用本文:2] |
| [6] | Xie Feng, Chen Zhen, Xu Hongfeng, et al. TST:threshold based similarity transitivity method in collaborative filtering with cloud computing[J]. Tsinghua Science and Technology, 2013, 18(3):318-327.[引用本文:1] |