针对L阵的二维波达方向估计问题,提出了一种低计算复杂度、高精度的二维波达方向估计算法.首先利用L阵子阵互相关矩阵和均匀线阵导向矢量的共轭交换性质扩展阵列孔径,并构造新的阵列接收数据;然后利用旋转不变子空间算法得到二维角度估计;最后将子阵互相关矩阵对角元素Toeplitz化,在不损失阵列孔径的情况下重构出类阵列自相关矩阵,利用Nystöm方法得到信号子空间估计,进而通过少量角度搜索得到正确的二维角度配对.该算法无须大量角度搜索,具有角度估计精度高、运算量小、所需快拍数少的优点.理论分析和仿真实验结果证明了算法的正确性和有效性.
A 2-D direction of arrival estimation method for L-shaped array with low computation complexity and high accuracy was presented. Firstly, the subarray cross-correlation matrix of L-shaped array and the conjugate exchange properties of the uniform linear array steering vectors is given, the proposed method extends the array aperture and constructs a new array received data matrix as well. Then the estimations of 2-D angles is obtained with the estimating of signal parameters via rotation invariance techniques algorithm. Finally, the subspace is estimated via applying the Nystöm method to the autocorrelation-like matrix, which is reconstructed by Toeplitzation-the diagonal elements of the subarray cross-correlation matrix without loss of the array aperture. Therefore, the correct angle pairing is achieved with a few angle search. The proposed method does not require massive angle search, and is high in the angle estimation accuracy, low in computation complexity and few in the necessary number of snapshots. Simulation is presented to validate the correction and effectiveness of the proposed method.
二维波达方向(2-D DOA,two dimensional direction of arrival)估计在通信、雷达等领域已有了广泛的应用. 由于L阵具有很好的二维角度估计性能[1],针对L阵的2-D DOA估计已有很多研究成果[2, 3, 4, 5, 6]. Hua等[1]提出最大似然角度估计算法,该算法具有接近克拉美罗下界(CRLB,Cramer-Rao lower bound)的优异的角度估计性能,但是需要二维搜索,运算量巨大. 针对如何降低运算量这一问题,Tayem等[2]提出的传播算子-旋转不变子空间(PM-ESPRIT,propagator method-estimating of signal parameters via rotation invariance techniques)算法,虽然运算量小,但是低信噪比低快拍情况下性能差. Wang等[3]所提基于互相关的计算有效的二维波达方向估计(CODE,computationally efficient cross-correlation based 2-D DOA estimation)算法,和Xi等[4]所提计算有效的子空间(CESA,computationally efficient subspace algorithm)算法,虽然将二维角度搜索转化为两次一维角度搜索,但是运算量依然很大.
上述这些算法或需要大量的角度搜索,运算量大,或低信噪比、低快拍情况下性能差. 针对这些问题,笔者首先利用L阵子阵互相关矩阵,构造新的阵列接收数据,然后采用旋转不变子空间(ESPRIT,estimating of signal parameters via rotation invariance techniques)算法得到二维角度估计,最后利用子阵互相关矩阵对角元素构造类阵列自相关矩阵,并对其利用Nystöm方法得到信号子空间估计,从而通过一维简单搜索得到正确配对的二维角度估计值. 与现有算法相比,所提算法具有角度估计精度高、运算量小、所需快拍数少的优点,非常适合于需要快速角度估计的实际应用场合.
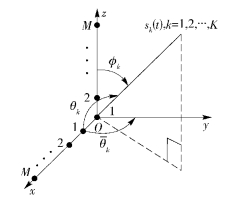
1 数据模型如图 1所示,假设t时刻(其中t=1,2,…,N,N为快拍数)有K个载波波长为λ的互不相关的窄带远场信号$\{ {s_k}(t)\} _{k = 1}^K$入射到由2M个阵元构成的L阵,阵元分别在x-z轴上,且x轴和z轴的子阵均为间距为d的M阵元均匀线阵. K个信号对应的方位角和俯仰角分别为$\{ ({\bar \theta _k},{\phi _k})\} _{k = 1}^K$,则x子阵与z子阵接收到的信号为[3]
| $X(t) = {A_\theta }S(t) + {N_x}(t)$ | (1) |
| $Z(t) = {A_\phi }S(t) + {N_z}(t)$ | (2) |
其中:接收信号矢量$X(t) = {[{x_1}(t),{x_2}(t),\cdots ,{x_M}(t)]^{\rm{T}}}$,$Z(t) = {[{z_1}(t),{z_2}(t),\cdots ,{z_M}(t)]^{\rm{T}}}$,信源信号矢量为$S(t) = {[{s_1}(t),{s_2}(t),\cdots ,{s_K}(t)]^{\rm{T}}}$. 为了简化表达,与文献[4]类似,定义伪方位角为θk,且$\cos {\theta _k} = \cos {\bar \theta _k}\sin {\phi _k}$,则x子阵和z子阵的流形矩阵可以分别表示为${A_\theta } = [a({\theta _1}),a({\theta _2}),\cdots ,a({\theta _K})]$,${A_\phi } = [a({\phi _1}),a({\phi _2}),\cdots ,a({\phi _K})]$,其中第k个信号对应 的子阵导向矢量为$a({\theta _K}) = {[1,{\xi _k},\cdots \xi _k^{M - 1}]^{\rm{T}}}$,$a({\phi _K}) = {[1,{\eta _k},\cdots \eta _k^{M - 1}]^{\rm{T}}}$,${\xi _k} = \exp ({\rm{j}}2\pi d\cos {\theta _k}/\lambda )$,${\eta _k} = \exp ({\rm{j}}2\pi d\cos {\phi _k}/\lambda )$. x子阵和z子阵接收信号的加性噪声分别为${N_x}(t) = {[{n_{x1}}(t),{n_{x2}}(t),\cdots ,{n_{xM}}(t)]^{\rm{T}}}$和 ${N_z}(t) = {[{n_{z1}}(t),{n_{z2}}(t),\cdots ,{n_{zM}}(t)]^{\rm{T}}}$,且假定加性噪声为方差σn2的零均值高斯白噪声,且与信号相互独立. 上标T表示矩阵转置.
2 算法原理构造x子阵和z子阵互相关矩阵为
| $\begin{array}{l} {R_{xz}} = E\{ X(t){Z^{\rm{H}}}(t)\} = \\ {A_\theta }E\{ S(t){S^{\rm{H}}}(t)\} A_\phi ^{\rm{H}} + E\{ {N_x}(t)N_z^{\rm{H}}(t)\} = \\ {A_\theta }{R_{ss}}A_\phi ^{\rm{H}} \end{array}$ | (3) |
式(3)中,由于噪声为零均值高斯白噪声,有$E\{ {N_x}(t)N_z^{\rm{H}}(t)\} = 0$. 同时由信号不相关可知,信号相关矩阵${R_{{\rm{ss}}}} = {\rm{diag}}\{ {p_1},{p_2},\cdots ,{p_k}\} $,$\{ {p_k}\} _{k = 1}^K$表示信号功率,diag{·}表示对角化,上标H表示共轭转置.
2.1 快速2-D DOA估计Thakre等[5]指出均匀线阵流形矩阵具有共轭交换性质,将其扩展应用于L阵可得
| ${J_M}{A_\theta }* = {A_\theta }\Phi _\theta ^{ - (M - 1)}$ | (4) |
| $A_\phi ^{\rm{T}}{J_M} = \Phi _\theta ^{M - 1}A_\phi ^{\rm{H}}$ | (5) |
| ${J_M}{A_\phi }* = {A_\theta }\Phi _\phi ^{ - (M - 1)}$ | (6) |
| $A_\theta ^{\rm{T}}{J_M} = \Phi _\theta ^{M - 1}A_\theta ^{\rm{H}}$ | (7) |
其中:上标*表示共轭;JM为M×M阶交换矩阵,即其反对角线元素全为1且其他元素均为0;${\Phi _\theta } = {\rm{diag}}\{ {\xi _1},{\xi _2},\cdots ,{\xi _K}\} $,${\Phi _\phi } = {\rm{diag}}\{ {\eta _1},{\eta _2},\cdots ,{\eta _K}\} $.
根据式(1)和式(2)可知,伪方位角θ和俯仰角Φ的估计可以独立进行. 下面以求解伪方位角θ为
例,首先构造方位增广互相关矩阵Raug(θ):
| ${R_{{\rm{aug}}}}(\theta ) = \left[{\begin{array}{*{20}{c}} {{R_{xz}}}\\ {{J_M}{R_{xz}}*{J_M}} \end{array}} \right]$ | (8) |
根据式(4)和式(5)且Rss=Rss*有
| $\begin{array}{l} {R_{{\rm{aug}}}}(\theta ) = \left[{\begin{array}{*{20}{c}} {{A_\theta }{R_{{\rm{ss}}}}A_\phi ^{\rm{H}}}\\ {{J_M}({A_\theta }{R_{{\rm{ss}}}}A_\phi ^{\rm{H}})*{J_M}} \end{array}} \right] = \\ \left[{\begin{array}{*{20}{c}} {{A_\theta }{R_{{\rm{ss}}}}}\\ {{A_\theta }\Phi _\theta ^{ - (M - 1)}{R_{{\rm{ss}}}}\Phi _\phi ^{M - 1}} \end{array}} \right]A_\phi ^{\rm{H}} = {A_{{\rm{aug}}}}(\theta )A_\phi ^{\rm{H}} \end{array}$ | (9) |
由式(9)可知,Aaug(θ)的维数为2M×K,即利用共轭交换性质增加了x子阵的孔径.
根据均匀线阵导向矢量的特征可知Aaug(θ)满足旋转不变性,即
| ${{\tilde J}_1}{A_{{\rm{aug}}}}(\theta ){\Phi _\theta } = {{\tilde J}_2}{A_{{\rm{aug}}}}(\theta )$ | (10) |
其中:${{\tilde J}_1} = \left[{\begin{array}{*{20}{l}}{{I_{M - 1}}} & 0 & {{0_{M - 1}}} & 0\\{{0_{M - 1}}} & 0 & {{I_{M - 1}}} & 0\end{array}} \right]$,${{\tilde J}_2} = \left[{\begin{array}{*{20}{l}}0 & {{I_{M - 1}}} & 0 & {{0_{M - 1}}}\\0 & {{0_{M - 1}}} & 0 & {{I_{M - 1}}}\end{array}} \right]$,IM-1、0M-1分别表示维数为(M-1)×(M-1)的单位阵和零矩阵,0表示维数为(M-1)×1的零向量.
但是由于Aaug(θ)是未知的,令Us(θ)表示方位信号子空间,可知式(10)等价于
| ${{\tilde J}_1}{U_{\rm{s}}}(\theta ){\Psi _\theta } = {{\tilde J}_2}{U_{\rm{s}}}(\theta )$ | (11) |
其中:${\Psi _\theta } = {T^{ - 1}}{\Phi _\theta }T$,T-1为T的逆矩阵.
方位信号子空间Us(θ)可以通过对Rθ=Raug(θ)RaugH(θ)进行特征值分解或对Raug(θ)进行奇异值分解求得,但运算量较大. Qian等[6]指出,Nystöm方法能以较低的运算量得到信号子空间估计,同时对后续角度估计影响很小. 因此,方位信号子空间Us(θ)通过对Raug(θ)利用Nystöm方法得到.
由ESPRIT算法可知,式(11)的最小二乘解为
| ${\Psi _\theta } = {({{\tilde J}_1}{U_{\rm{s}}}(\theta ))}$†${{\tilde J}_2}{U_{\rm{s}}}(\theta )$ | (12) |
其中${( \cdot )}$†表示伪逆.
根据${\Psi _\theta } = {T^{ - 1}}{\Phi _\theta }T$可知,Φθ与Ψθ具有相同的特征值,而同时Φθ是一个对角阵,从而
| ${\Phi _\theta } = {\rm{angle}}({\rm{EVD}}({\Psi _\theta }))$ | (13) |
其中angle和EVD表示取相角和特征值分解.
根据式(13)及Φθ的定义可得到伪方位角估计值$\{ {{\hat \theta }_k}\} _{k = 1}^K$.
同理,对于俯仰角Φ,构造俯仰增广互相关矩阵Raug(Φ):
| ${R_{{\rm{aug}}}}(\phi ) = \left[{\begin{array}{*{20}{c}} {R_{xz}^{\rm{H}}}\\ {{J_M}R_{xz}^{\rm{H}}{J_M}} \end{array}} \right]$ | (14) |
采用与Raug(θ)类似的处理过程,对Raug(Φ)利用Nystöm方法得到俯仰子空间估计Us(Φ),进而利用ESPRIT算法可以得到俯仰角估计值$\{ {{\hat \phi }_k}\} _{k = 1}^K$.
2.2 角度配对虽然2.1节得到了伪方位角和俯仰角的估计值,但是需要配对才能得到信号位置的估计.
根据L阵接收数据特征可知,Rxz的对角元素可表示为
| ${r_{{\rm{diag}}}} = ({A_\theta }* \odot {A_\phi }){r_{{\rm{ss}}}}$ | (15) |
其中,⊙表示Hadamard积,${r_{{\rm{ss}}}} = {[{p_1},{p_2},\cdots {p_k}]^{\rm{T}}}$.
利用rdiag构成Toeplitz矩阵RθΦ:
| ${R_{\theta \phi }} = {\rm{Toeplitz(}}{r_{{\rm{diag}}}}{\rm{) = }}({A_\theta }* \odot {A_\phi }){R_{{\rm{ss}}}}{({A_\theta }* \odot {A_\phi })^{\rm{H}}}$ | (16) |
其中Toeplitz(·)表示以原向量元素构成新的Toeplitz矩阵.
对RθΦ利用Nystöm方法得到信号子空间Us(θ,Φ),然后构造如下的代价函数f(θ,Φ):
| $f(\theta ,\phi ) = \frac{1}{{{{\tilde a}^{\rm{H}}}(\theta ,\phi )(I - {{\tilde U}_s}(\theta ,\phi )\tilde U_s^{\rm{H}}(\theta ,\phi ))\tilde a(\theta ,\phi )}}$ | (17) |
其中:${{\tilde a}^{\rm{H}}}(\theta ,\phi ) = a*(\theta ) \odot a(\phi )$,${{{\tilde U}_s}(\theta ,\phi )}$是通过对Us(θ,Φ)按列进行Gram-Schmidt正交化得到.
将得到的伪方位角和俯仰角的估计值$\{ {{\hat \theta }_k}\} _{k = 1}^K$、$\{ {{\hat \phi }_k}\} _{k = 1}^K$代入式(17),重复图 2中伪码表示的过程.
根据配对的伪方位角和俯仰角的估计值$\{ {{\hat \theta }_k}\} _{k = 1}^K$、$\{ {{\hat \phi }_k}\} _{k = 1}^K$求出方位角的估计值,即
$ {{\mathop {\bar \theta }\limits^ \wedge }_k} = \arccos (\cos {{\hat \theta }_K}/\sin {{\hat \theta }_K}) $
2.3 算法分析笔者提出的算法与Xi等[4]提出的CESA算法都将阵列的孔径扩展为原来的2倍,但是CESA算法重构矩阵后仅利用了(2M-K)个阵元的数据,损失了扩展的阵列孔径,而笔者重构矩阵利用了2M个阵元的数据,没有损失扩展的阵列孔径,因而所提出的算法的角度估计精度更高.
CESA算法由于采用了类多重信号空间分类(MUSIC-Like,multiple signal classification-like)的角度估计算法,需要两次大量的一维角度搜索. 其计算复杂度主要体现在2次角度搜索,计算复杂度为$O(({N_\theta } + {N_\phi })(K + 1){(2M - K)^2})$,这里Nθ、NΦ表示方位角和俯仰角搜索的次数.
笔者提出的算法采用ESPRIT算法估计角度,除去配对过程的少量角度搜索,无需大量的角度搜索,其计算复杂度主要体现在采用Nystöm方法估计信号子空间及利用ESPRIT算法求解角度,计算复杂度为$O(5{M^2}K + 5M{K^2} + 4{K^3})$.
一般情况下,${N_\theta },{N_\phi } \gg M$且M>K,根据上述2个算法的运算复杂度表达式可知,在Nθ,NΦ≥1 800(角度搜索范围为0°~180°,角度搜索间隔≤0.1°)且M≤180的情况下,显然所提出的算法比CESA算法具有更低的计算复杂度.
3 仿真分析为了验证所提算法的正确性和有效性,与CESA算法及CRLB做对比,进行如下仿真实验.
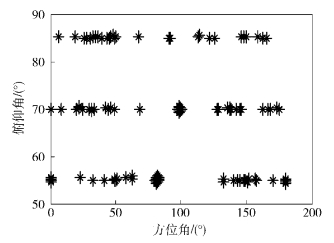
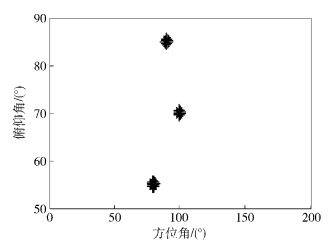
3.1 实验设置仿真实验1 为了比较所提算法与CESA算法的角度估计与配对性能,假定x和z子阵阵元数M=8,子阵阵元间距d=λ/2,3个信号的方位角和俯仰角分别为(80°,55°)、(90°,85°)、(100°,70°),快拍数N=512. CESA算法角度搜索范围为0°~180°,角度搜索间隔0.1°. 信噪比为0 dB,进行500次蒙特卡洛仿真实验,两种算法得到的角度估计及配对结果如图 3和图 4所示.
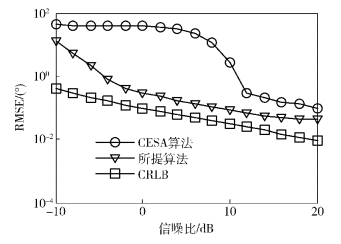
仿真实验2 为了比较所提算法与CESA算法的角度估计及配对性能随信噪比的变化,假定除信噪比外,其他仿真条件同仿真实验1,改变信噪比,使其从-10 dB变化到20 dB,间隔2 dB,每个信噪比下进行500次蒙特卡洛仿真实验,角度估计的均方根误差(RMSE,root mean square error)随信噪比变化结果如图 5所示(${\delta _{{\rm{RMSE}}}} = \sqrt {\sum\limits_{l = 1}^L {\sum\limits_{k = 1}^K {\left( {{{\left( {{\mathop {\bar \theta }\limits^ \wedge} _k^{(l)} - {{\bar \theta }_k}} \right)}^2} + {{\left( {\hat \phi _k^{(l)} - {\phi _k}} \right)}^2}} \right)} } } $,L为蒙特卡洛仿真次数,${{\mathop {\bar \theta }\limits^ \wedge} _k^{(l)}}$和${\hat \phi _k^{(l)}}$分别为第l次蒙特卡洛仿真实验得到的第k个信号的方位角和俯仰角的估计值).
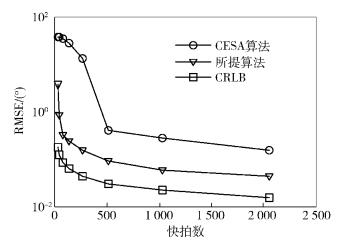
仿真实验3 为了比较所提算法与CESA算法的角度估计与配对性能随快拍数的变化,假定除信噪比和快拍数外,其他仿真条件同仿真实验1,固定信噪比10 dB,改变快拍数,从24变化到211,每个快拍数下进行500次蒙特卡洛仿真实验,角度估计RMSE随快拍数变化结果如图 6所示.
仿真实验4 为了比较所提算法与CESA算法的运算复杂度,假定除子阵阵元数M外,其他仿真条件同仿真实验1,改变子阵阵元数M,使其从8变化到128,间隔为8,不同阵元数下分别进行500次蒙特卡洛仿真实验,统计两种算法在不同子阵阵元数M下的平均运行时间,结果如图 7所示.
3.2 实验分析由图 3和图 4可知,所提算法角度估计RMSE比CESA算法低,同时在低信噪比情况下,所提配对算法比CESA算法对应的角度配对算法具有更高的成功配对率.
由图 5可知,所提算法角度估计的RMSE随信噪比的增加而降低,验证了所提算法的有效性. 同时与CESA算法相比,所提算法RMSE更低,表明所提算法具有更高的角度估计精度,进一步验证了2.3节所述算法的孔径扩展能力.
由图 6可知,所提算法角度估计的RMSE随快拍数的增加而降低,进一步验证所提算法的有效性. 同时由图 6可知,所提算法相对于CESA算法达到相同的角度估计精度所需的快拍数少得多,这对于实际快拍数较少的应用场合很重要.
由图 7可知,所提算法平均运行时间比CESA算法运行时间要少得多,在子阵阵元数M≤128且角度搜索精度为0.1°时,所提算法平均运行时间不超过CESA算法运算量的2%,进一步验证了2.3节针对所提算法计算复杂度的分析.
4 结束语笔者将均匀线阵流形矩阵的共轭交换性质扩展应用于L阵,增加了阵列的孔径,进而提高了角度估计的精度,同时利用Nystöm方法得到信号子空间的估计并利用ESPRIT算法估计角度,无须大量角度搜索,降低了运算量. 所提出的算法具有角度估计精度高、运算量小、所需快拍数少的优点,非常适合于实时性要求较高且快拍数较少的场合. 但是注意到所提角度配对算法在信号部分相关甚至相干时,信号相关矩阵Rss不能近似为对角阵,此时角度配对算法性能下降甚至失效,因此在将来会研究一种可工作在部分相关甚至相干情形下的角度配对算法. 另一方面,由于所提算法需要角度配对,而且在低信噪比下存在误配,影响该算法的使用,因此下一步需要研究一种基于L阵的无须配对的快速2-D DOA估计算法.
| [1] | Hua Yingbo, Saker T, Weiner D. An L-shaped array for estimating 2-D directions of wave arrival[J]. IEEE Trans on Antennas Propag, 1991, 39(2):143-146.[引用本文:2] |
| [2] | Tayem N, Kwon H M. L-shape 2-dimensional arrival angle estimation with propagator method[J]. IEEE Trans on Antennas Propag, 2005, 53(5):1622-1630.[引用本文:2] |
| [3] | Wang Guangmin, Xin Jingmin, Zheng Nanning, et al. Computationally efficient subspace-based method for two-dimensional direction estimation with L-shaped array[J]. IEEE Trans on Signal Process, 2011, 59(7):3197-3212.[引用本文:3] |
| [4] | Xi Nie, Li Liping. A computationally efficient subspace algorithm for 2-D DOA estimation with L-shaped array[J]. IEEE Signal Process Letters, 2014, 21(8):971-974.[引用本文:4] |
| [5] | Thakre A, Haardt M, Giridhar K. Single snapshot spatial smoothing with improved effective array aperture[J]. IEEE Signal Process Letters, 2009, 16(6):505-508.[引用本文:2] |
| [6] | Qian Chen, Huang Lei, So H. C. Computationally efficient ESPRIT algorithm for direction-of-arrival estimation based on Nystöm method[J]. Signal Process, 2014, 94:74-80.[引用本文:2] |