2. 江苏省无线传感网高技术研究重点实验室, 南京 210003;
3. 北京邮电大学 网络与交换技术国家重点实验室, 北京 100876
针对多媒体传感网采集图像信息的空间冗余问题,提出了一种面向数据压缩的无线多媒体传感器网络节点的选择方法.该方法从节点3维感知模型出发,设计空间相关模型以描述感知图像数据之间的相关性,在此基础上,提出基于相关性的节点选择方法,减少了采集数据的空间冗余.仿真实验结果验证了新方案的有效性.
2. Jiangsu High Technology Research Key Laboratory for Wireless Sensor Networks, Nanjing 210003, China;
3. State Key Laboratory of Networking and Switching Technology, Beijing University of Posts and Telecommunications, Beijing 100876, China
Multimedia sensor network is an advanced form of sensor networks. It has multimedia information perception, processing and transmission capacity. For the problem of great redundancy and correlation in the collection data, a node selection approach for data compression was designed. By using the correlation model based on three-dimensional perception, it describes the relevant characteristics between the observed images data. Then the camera node selection algorithms was proposed based on correlation coefficients to reduce the spatial redundancy of sensing data. A set of comparisons are performed to evaluate the effective of our algorithms.
近年来,无线多媒体传感器网络(WMSNs,wireless multimedia sensor networks)作为一种新兴的网络模式引起了研究者的广泛关注[1],WMSNs视觉信息的获取和处理相比传统标量信息需要更多的带宽和更高的处理能力,单个相机传感节点直接感知自身视野数据,空间位置接近节点对应感知区域,必然存在重叠[2]. 通常导致相邻相机节点获得的视觉信息高度相关,使网络中的数据具有相当大冗余,严重消耗节点能量. 针对该问题,笔者在前期工作[3]的基础上,研究了基于空间相关的无线多媒体传感网节点选择方法.
Wang等[4]设计了一个基于空间相关性的无线多媒体传感网图像压缩框架;Mowafi等[5]研究了不同感知半径和视角的节点部署问题. Alaei等[6]对多媒体传感器节点分簇聚合,将感知视角(FoV,field of view)作为分簇的重要依据. 韩崇等[7]提出了基于网格划分的多媒体传感网时空覆盖调度算法. 但上述研究都是针对传统2维相机感知模型. 在现实情况中,相机节点模型和实际感知环境都是3维结构,传统2维相机感知模型很难直接应用于物理现实环境. Ma等[8]提出了相机节点的3维感知模型. Han等[9]设计了FoV相关性模型来描述相机之间由重叠的FoV产生的相关特性,并进一步提出了2种计算节点FoV相关性的方法. Nevat等[10]则对2维标量节点的空间相关随机域进行估计,设计了新的算法对节点的空间域重建、估计和分类. 不同于Han等[9]提出的相关性模型,笔者设计了新的相关性模型以描述相机两两之间由重叠的FoV产生的相关特性,并提出了基于空间相关性的节点选择方法来对WMSNs中的相机节点进行选择,实现感知数据的去空间冗余,从而降低节点能耗.
1 节点空间相关性模型 1.1 3维有向感知模型[3]3维空间中的无线多媒体传感器节点的感知模型取决于节点的空间坐标、水平感知方向和垂直方向的最大张角. 传感器节点的覆盖区域为一个等腰梯形. 笔者采用前期研究[3]设计的多媒体传感器节点3维感知模型,如图 1所示.
多媒体传感器节点3维感知模型可由一个四元组(P, C, α, β)表示. 其中:P=(x, y, z)为节点在3维空间中的坐标;C=(γ, θ)为节点的感知方向,γ为仰俯角,θ为偏向角;2α为水平方向上节点的感知视角,2β为垂直方向上节点的感知视角. 在监测区域内,传感器节点随机分布,节点的主感知方向C的值一般也为随机分布,θ的取值范围为[0, 2π],γ的取值范围为[0, π/2).
1.2 相关性模型在多媒体传感网中,部署在监测场景中的若干相机传感器节点是为了实现对环境的多视角、全方位监测和数据感知. 如图 2所示,相机节点随机部署于监测环境中,每个相机节点只能对自己的FoV进行监测感知,不同相机节点之间的FoV可能发生重叠. 对应感知数据中存在较大的空间相关性,导致多媒体传感网感知数据的空间冗余.
当部署在监测场景中的所有相机节点位置固定,且满足下列条件:所有相机都被固定于同样的高度,所有节点同构,具有相同的俯仰角、最大水平感知视角2α和垂直感知视角2β,而决定相机节点感知方向的θ角可能不同. 因梯形区域形状大小由γ、α、β决定,所以不同相机节点的对应感知区域大小保持一致. 在满足上述条件时,部署在环境中的相机节点拥有相同大小的感知区域和不同感知方向.
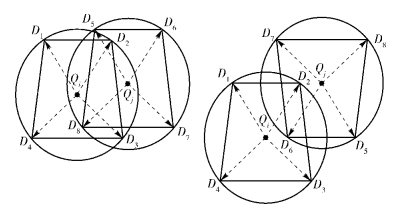
定义1 设相机节点Ci感知区域D1D2D3D4的外接圆圆心为点Qi,相机节点Cj感知区域D5D6D7D8的外接圆圆心为点Qj,则2个相机节点感知区域的外接圆圆心之间的距离为|QiQj|,如图 3所示.
定义相机节点Ci与Cj之间的相关系数为
| ${\rho _1} = \left\{ {\begin{array}{*{20}{l}} {0, \;\;|{Q_i}{Q_j}| \ge 2r}\\ {1 - \frac{{|{Q_i}{Q_j}|}}{{2r}}, \;\;|{Q_i}{Q_j}| < 2r} \end{array}} \right.$ | (1) |
其中r为相机节点感知区域的外接圆半径.
当ρ1值越小时,相机节点Ci与Cj的感知区域外接圆圆心距离越近,节点Ci与Cj整体上越相关.
定义2 由相机节点Ci感知区域D1D2D3D4的外接圆圆心Qi向D1、D2、D3、D4作向量${{{\overrightarrow {{Q_i}D} }_1}}$、${{{\overrightarrow {{Q_i}D} }_2}}$、${{{\overrightarrow {{Q_i}D} }_3}}$、${{{\overrightarrow {{Q_i}D} }_4}}$,由相机节点Cj的感知区域D5D6D7D8的外接圆圆心Qj向D5、D6、D7、D8作向量${{{\overrightarrow {{Q_j}D} }_5}}$、${{{\overrightarrow {{Q_j}D} }_6}}$、${{{\overrightarrow {{Q_j}D} }_7}}$、${{{\overrightarrow {{Q_j}D} }_8}}$,如图 4所示.
分别计算$|{\overrightarrow {{Q_i}D} _1} - {\overrightarrow {{Q_j}D} _5}|$、$|{\overrightarrow {{Q_i}D} _2} - {\overrightarrow {{Q_j}D} _6}|$、$|{\overrightarrow {{Q_i}D} _3} - {\overrightarrow {{Q_j}D} _7}|$、$|{\overrightarrow {{Q_i}D} _4} - {\overrightarrow {{Q_j}D} _8}|$的值,然后取它们的平均值为
| $\begin{array}{l} {\delta _{ij}} = \frac{1}{4}(|{\overrightarrow {{Q_i}D} _1} - {\overrightarrow {{Q_j}D} _5}| + |{\overrightarrow {{Q_i}D} _2} - {\overrightarrow {{Q_j}D} _6}| + \\ |{\overrightarrow {{Q_i}D} _3} - {\overrightarrow {{Q_j}D} _7}| + |{\overrightarrow {{Q_i}D} _4} - {\overrightarrow {{Q_j}D} _8}| \end{array}$ | (2) |
定义相机节点Ci与Cj之间的相关系数为
| ${\rho _2} = 1 - \frac{{{\delta _{ij}}}}{{0.5(|{{\overrightarrow {{Q_i}D} }_1}| + |{{\overrightarrow {{Q_i}D} }_2}| + |{{\overrightarrow {{Q_i}D} }_3}| + |{{\overrightarrow {{Q_i}D} }_4}|)}}$ | (3) |
ρ2为相机节点偏向角θ的另一种表现形式. 当Ci与Cj的偏向角θ相等时,ρ2取最大值为1;当Ci与Cj的偏向角相差π时,ρ2取最小值为0. 对应2种情况如图 5所示.
定义3 3维空间中的多媒体传感网,对于任意2个相机传感器Ci和Cj,假设在同一时间它们感知到的图像分别为Xi和Xj. 当Xi和Xj发生重叠时,Xi和Xj对应的相关系数为ρij. ρij可较准确地表示相机节点Ci与Cj感知获取的图像Xi和Xj之间的相关性.
| ${\rho _{ij}} = \left\{ {\begin{array}{*{20}{l}} {0, \;\;\;\;|{Q_i}{Q_j}| \ge 2r}\\ {\alpha {\rho _1} + \beta {\rho _2}, \;\;\;|{Q_i}{Q_j}| < 2r} \end{array}} \right.$ | (4) |
其中:0<α≤1,0≤β<1,α+β=1.
2 基于相关性的节点选择方法假定无线多媒体传感器网络对应的监测区域内有总数为N的相机传感器节点可进行感知获取监测图像. 如果网络资源允许,所有节点传输感知图像信息给汇聚节点,汇聚节点可得区域总信息. 但考虑到相机节点处理能力有限,且大数据量的传输也会消耗网络能量,笔者考虑基于节点的空间相关性,进行采集数据节点的有效选择,在保证监测场景数据整体完整的同时,尽可能降低节点数量.
对应为相机节点的选择问题:如果M个相机(M≤N)可传输它们感知的图像数据至汇聚节点,考虑从N个相机中选择M个节点使汇聚节点尽可能获得最多的信息,即尽可能地减少数据冗余. 相机节点之间的相关性越小,它们能提供的信息越多. 所以为了使汇聚节点获得的信息最大化,笔者尝试使选中的所有相机节点相关性最小.
依据贪心准则设计一个基于相关性的相机节点选择方法来选择M个相机节点向汇聚节点传输感知图像信息. 具体步骤如下.
初始状态 相机节点集S中有N个相机节点,由相关性模型计算出相机节点两两之间的相关系数,得N维矩阵(ρij)N×N.
步骤1 从矩阵(ρij)N×N中找出相关系数最小的一对相机节点,将它们加入选择节点集Q(当M=2时结束).
步骤2 计算相机节点集中的每个未加入Q的节点与选择节点集Q中的节点的相关系数的平均值,选出与节点集Q中平均值最小的节点,将其加入选择节点集Q.
步骤3 当选择节点集Q中的节点数小于M时,重复步骤2.
步骤4 当选择节点集Q中的节点数等于M时,选择结束,得选择节点集Q. Q中有M个相机节点,即当该M个相机节点向汇聚节点传输感知图像信息时,可得最佳效果.
3 实验及分析 3.1 3维感知的节点相关性模型评价1) 相关系数的有效性
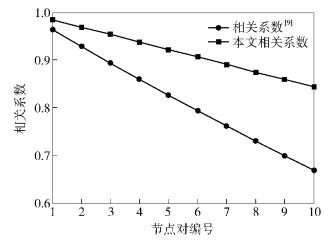
假设场景:相机节点1和节点2均部署于同一监测区域中监测感知图像数据. 它们固定于10 m高,俯仰角γ同为58°,最大水平感知视角2α为60°,最大垂直感知视角2β为50°;偏向角θ同为10°. 相机节点的x坐标、y坐标随机产生;产生的相机节点坐标的水平方向距离逐渐增大;相关系数ρij中的系数α=1,β=0. 实验计算的2个节点1之间的相关系数和文献[9]对应模型的相关系数结果如图 6所示.
从图 6可以看出,当相机节点的部署坐标越接近,相机之间的水平距离越近,笔者提出的相机之间的相关系数越大,相机之间越具有相关性,与文献[9]的相关系数拥有相同的变化趋势. 因为相机节点坐标越接近,它们的感知区域之间的重叠区域越大,相机之间越具有相关性.
2) 能量消耗的对比
主要讨论笔者提出的3维节点感知相关性模型与文献[9]相关性模型的能量消耗.
如果相机节点想知道彼此的相关特性,即计算彼此之间的相关系数,就需要传感器节点之间进行通信计算. 笔者提出的相关性模型在计算节点之间相关系数时,只需确定相机节点感知区域等腰梯形的顶点坐标和梯形外接圆圆心坐标,然后进行一些简单的向量加减和长度计算即可. 对应的计算时间复杂度为O(n12lbN). 其中:N为监测场景中部署的相机节点个数,n1为对某个节点感知区域的外接圆圆心距离小于2r的节点数. 而Han等[9]提出的相关性模型有2种计算相机之间相关系数的方法. 第1种为基于网格划分的计算方法,该方法将整个监测环境区域划分为尽可能小的网格. 在计算2个相机节点之间的相关系数时,需遍历节点感知区域覆盖的所有网格,网格划分越小,对应计算量越大. 第2种为基于相关位置的计算,该方法需确定一个相机节点感知区域的顶点是否位于另一个相机节点的感知区域内,计算求出2个节点感知区域的交点,最后将所得点集按一定顺序排列,才能计算对应的相关系数. 计算时间复杂度为O(Nn22lbN),其中n2为与某个节点感知区域重叠的节点数. 第2种计算方法与第1种计算方法相比,虽减少了2个数量级的时间复杂度[13],但与笔者提出的相关性模型相比,仍需大量的计算,产生较多的能量消耗.
3.2 节点选择方法评价在一个100 m×100 m×10 m的监测区域中,随机部署N个相机节点进行监测感知,汇聚节点选择M个相机节点向其传输它们感知的图像. 假设每个相机节点可获得1幅感知图像. 设{X1, X2, …, XN}为N个相机节点感知的图像. 假设1个单独图像的熵为某一恒定值,设H(Xi)=0.5(i=1, 2, …, N). 对于部署在监测环境中的N个相机节点,根据第1节可得1个相关矩阵. 下面使用文献[2]中计算多节点联合熵的方法来比较以下2个节点选择方法的性能. 1)随机选择:从N个相机节点中随机选择M个相机节点. 2)基于相关性选择:基于相关性的节点选择方法考虑相关性来选择M个相关的相机节点,使选择相机节点的信息量尽可能最大化.
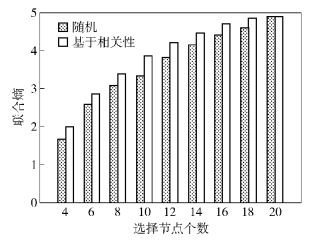
实验中,随机在监测区域中部署N个相机节点,节点总数为N=20时,每次使用笔者提出的节点选择方法选择相同数量的相机节点,实验结果如图 7所示.
可以看出,笔者基于相关性的节点选择方法得到的联合熵总是大于随机选择相机节点的信息熵. 从另一个角度看,如果汇聚节点有某一确定的联合熵临界,基于相关性的节点选择方法比随机选择方法需要更少的相机节点.
4 结束语针对WMSNs的相关性和数据冗余问题,从WMSNs相机节点的3维感知模型出发,提出了一个新的3维节点感知相关性模型来描述相机之间的相关特性,在此基础上提出了基于相关性的节点选择方法来对WMSNs中的节点进行选择,从而实现多媒体传感网感知数据的去空间冗余,仿真实验结果验证了新方案的有效性.
| [1] | Akyildiz I F, Melodia T, Chowdhury K R. A survey on wireless multimedia sensor networks[J]. Compute Networks, 2007, 51(4):921-960.[引用本文:1] |
| [2] | Dai Rui, Akyildiz I F. A spatial correlation model for visual information in wireless multimedia sensor networks[J]. IEEE Transaction on Multimedia, 2009, 11(6):1148-1159.[引用本文:2] |
| [3] | 肖甫, 王汝传, 孙力娟, 等. 一种面向三维感知的无线多媒体传感器网络覆盖增强算法[J]. 电子学报, 2012, 40(1):167-172. Xiao Fu, Wang Ruchuan, Sun Lijuan, et al. Coverage-enhancing algorithm for wireless multi-media sensor networks based on three-dimensional perception[J]. Acta Electronica Sinica, 2012, 40(1):167-172.[引用本文:3] |
| [4] | Wang Pu, Dai Rui, Akyildiz I F. A spatial correlation-based image compression framework for wireless multimedia sensor networks[J]. IEEE Transaction on Multimedia, 2011, 13(2):388-401.[引用本文:1] |
| [5] | Mowafi M Y, Awad F H, Aljoby W A. Spatial correlation model for heterogeneous cameras in wireless multimedia sensor networks[C]//WoWMoM 2013. Madrid:IEEE Press, 2013:1-6.[引用本文:1] |
| [6] | Alaei M, Barcelo-Ordinas J M. Node clustering based on overlapping FoVs for wireless multimedia sensor networks[C]//WCNC 2010. Sydney:IEEE Press, 2010:1-6.[引用本文:1] |
| [7] | 韩崇, 孙力娟, 郭剑. 一种基于网格划分的有向传感网时空覆盖调度算法[J]. 南京邮电大学学报(自然科学版), 2013, 33(5):82-87. Han Chong, Sun Lijuan, Guo Jian. A scheduling algorithm for spatial-temporal coverage in the directional sensor networks based on grid partition[J]. Journal of Nanjing University of Posts and Telecommunications (Natural Science), 2013, 33(5):82-87.[引用本文:1] |
| [8] | Ma Huadong, Zhang Xi, Ming Anlong. A coverage-enhancing method for 3D directional sensor networks[C]//INFOCOM 2009. Washington:IEEE Press, 2009:2791-2795.[引用本文:1] |
| [9] | Han Chong, Sun Lijuan, Xiao Fu, et al. FoVs correlation model for wireless multimedia sensor networks based on three-dimensional perception[J]. Advances in Information Sciences and Service Sciences, 2012, 4(3):27-34.[引用本文:6] |
| [10] | Nevat I, Peters G W, Septier F, et al. Estimation of spatially correlated random fields in heterogeneous wireless sensor networks[J]. IEEE Transactions on Signal Processing, 2015, 63(10):2597-2609.[引用本文:1] |