2. 宁夏沙漠信息智能感知重点实验室, 银川 750021;
3. 北京邮电大学 信息与通信工程学院, 北京 100876
针对Goldstein枝切线法存在的问题,根据残差点的分布特点,提出了一种新的干涉合成孔径雷达相位解缠方法.该方法首先对邻近偶极子对进行预处理,生成独立且长度很短的枝切线,使用自适应遗传模拟退火算法计算剩余正负残差点的优化组合,不仅在短时间内设置出总体长度较短的枝切线,且有效地避免了大面积"孤岛"出现.实验结果表明,相比于几种典型的相位解缠算法,该方法在时间和精度上具有优越性.
2. Ningxia Key Laboratory of Intelligent Sensing for Desert Information, Yinchuan 750021, China;
3. School of Information and Communication Engineering, Beijing University of Posts and Telecommunications, Beijing 100876, China
Due to disadvantages of Goldstein's branch cut algorithm, a new phase unwrapping method for interferometric synthetic aperture radar (INSAR) was proposed according to distribution characteristics of residue. Firstly, the neighbor dipoles preprocessing algorithm was performed to establish independent and short branch cuts. Secondly, the adaptive genetic simulated annealing algorithm was performed to calculate optimized combination of remaining residues. Ultimately, the branch cuts with short length was generated in a short time, and large "isolated island" phenomenon was avoided. Experiment shows that the proposed method has advantages in precision and operation time compared with some typical phase unwrapping algorithm.
相位解缠作为干涉合成孔径雷达(INSAR,interferometric synthetic aperture radar)技术中最为关键的一步,其解缠结果的好坏将直接影响后期数字高程模型(DEM,digital elevation model)的精度. 围绕相位解缠问题,发展起来的代表性算法主要有路径跟踪法、最小范数法和网络流法三大类. 其中,以Goldstein等[1]提出的枝切线法最为经典和有效,在得不到DEM校准的情况下,它的解缠结果常被作为评判其他相位解缠算法结果的基准. 因此,一般也将其作为最先尝试的相位解缠算法. 但Goldstein法在残差点密集处设置的枝切线很难达到最短,且由于枝切线重复连接,容易形成大量不可解缠的封闭区域,产生“孤岛”现象[2],对后续高程反演造成一定影响.
笔者提出了一种将邻近偶极子对预处理和自适应遗传模拟退火算法相结合的相位解缠算法. 既实现了枝切线整体较短,也避免了大量“孤岛”出现,提高了解缠精度和速度. 最后给出实验结果和分析.
1 枝切截断与改进的枝切线法在INSAR信号采集与处理过程中,往往存在噪声、欠采样、透视收缩和地形剧烈起伏等问题,均会导致干涉相位场出现不一致的现象[3],在干涉条纹图中表现为残差点,这些残差点可以通过计算某点(i, j)的残差值Q(i, j)来确定[4],即
| $\begin{array}{l} Q(i, j) = W\{ \varphi (i, j + 1) - \varphi (i, j)\} + \\ W\{ \varphi (i + 1, j + 1) - \varphi (i, j + 1)\} + \\ W\{ \varphi (i + 1, j) - \varphi (i + 1, j + 1)\} + \\ W\{ \varphi (i, j) - \varphi (i + 1, j)\} \end{array}$ | (1) |
其中:W{*}为缠绕运算,当Q(i, j)>0时,该点为正残差点;当Q(i, j)<0时,该点为负残差点. 如果解缠路径包含了这些残差点,误差将会在全图传播.
枝切截断路径跟踪法(简称枝切线法)通过连接邻近的正负残差点,生成中性“枝状切线”. 在逐点解缠时,枝切线起到截断解缠路径的作用,从而避免了误差在全局进行传播. 但Goldstein枝切线法的原则是只要扫描到残差点就连接到当前枝切线,因此常常会出现枝切线过长和围成封闭区域等问题. 由于较短的枝切线在解缠过程中不仅更容易被避开,而且不易围成无法解缠的“孤岛”,同时又能降低在枝切线附近产生的累加误差. 因此,总长度越短,解缠效果越好[5].
为了构建出较短的枝切线,考虑将正负残差点两两匹配连接,那么每条枝切线都是中性的,可以起到隔绝误差的作用. 当正负残差点各有N个时,上述可能的连接方式就有N!种,对于任一种连接方式,其枝切线总长度可以表示为
| $f = \sum\limits_{i = 1}^n {\sqrt {{{(x_i^{{\rm{positive}}} - x_i^{{\rm{negative}}})}^2} + {{(y_i^{{\rm{positive}}} - y_i^{{\rm{negative}}})}^2}} } $ | (2) |
其中:${(x_i^{{\rm{positive}}}, y_i^{{\rm{positive}}})}$和${(x_i^{{\rm{negative}}}, y_i^{{\rm{negative}}})}$分别为第i个 匹配的正负残差点在干涉条纹图中的坐标. 为了使f达到最小,旅行商问题(TSP,traveling salesman problem)理论[6]、粒子群算法[7]等优化算法均被用来改善残差点的匹配方式. 然而,由于残差点数量直接关系到优化算法的计算时间和精度,因此当残差点数量较多时,直接使用优化算法会造成时间和空间复杂度的大幅增加,计算效率下降,在短时间内很难得出较优的解. 笔者所提方法采取邻近偶极子对预处理与优化算法相结合的方式,在较短时间内实现残差点的优化匹配.
1.1 邻近偶极子对预处理算法在干涉相位图中,残差点主要分为2类:偶极子对残差点和单极子残差点[8]. 其中,偶极子对残差点主要由随机相位噪声引起,以距离较近的正负残差点对的形式出现,而单极子残差点主要由目标不连续或没有遵循Nyquist采样定律造成,通常单独出现或正负残差点相距很远. 针对残差点的特点,提出了距离阈值R内的邻近偶极子对预处理算法. 具体步骤如下.
1) 分别将干涉相位图中的正负残差点标记为“+1”和“-1”极性,并对所有残差点标记为不平衡,设置距离阈值R.
2) 找到一个不平衡残差点,并以该残差点为中心,放置一个N×N(N=3)搜索窗. 若该残差点为边界点,转3),否则转4).
3) 在N×N搜索窗内搜索残差点,将所有找到的残差点与中心残差点用枝切线相连,并对每个残差点标记为平衡;若无其他残差点,则将中心残差点设置成枝切线,并标记为平衡,转2).
4) 在N×N搜索窗内搜索异性残差点,若找到,则在该残差点和中心残差点之间设置枝切线,并将这2个残差点标记为平衡,转2);若未找到,则判断搜索窗是否已到达图像边界,若已到达边界,则将该残差点与边界相连,标记为平衡后,转2),否则转5).
5) 令N=N+2,若N≤2R+1,转4);若N>2R+ 1,则放弃对该残差点的操作,转2).
重复步骤1)~5),遍历所有残差点后,若剩余不平衡的残差点数量不相等,则通过将最靠近边界的残差点与边界相连或增加边界点的方式来实现残差点数量平衡. 距离阈值R为大于等于1的整数,可根据图像大小和残差点数量自行设置.
1.2 自适应遗传模拟退火算法遗传算法(GA,genetic algorithm)和模拟退火算法(SA,simulated annealing)作为2种较为成熟的智能算法,在解决优化问题上得到了广泛应用. GA的优势在于全局搜索能力强,但容易出现过早收敛和陷入局部最优解等问题,局部搜索能力较弱. SA在接受优解的同时,还能有限度地接受恶化解,从而使算法从局部最优解中跳出,因此其局部搜索能力较强,但全局搜索能力较差. 针对2种算法存在的优缺点,提出了一种自适应遗传模拟退火算法,用于计算剩余不平衡残差点的优化组合. 算法中引入由Srinvivas算子改进后的自适应交叉概率Pc和变异概率Pm为
| ${P_{\rm{c}}} = \left\{ {\begin{array}{*{20}{l}} {{P_{{\rm{c}}1}} - \frac{{({P_{{\rm{c}}1}} - {P_{{\rm{c2}}}})(f' - {f_{{\rm{avg}}}})}}{{{f_{\max }} - {f_{{\rm{avg}}}}}}, \;\;f' \ge {f_{{\rm{avg}}}}}\\ {{P_{{\rm{c}}1}}, \;\;f' < {f_{{\rm{avg}}}}} \end{array}} \right.$ | (3) |
| ${P_{\rm{m}}} = \left\{ {\begin{array}{*{20}{l}} {{P_{{\rm{m}}1}} - \frac{{({P_{{\rm{m}}1}} - {P_{{\rm{m2}}}})({f_{\max }} - f)}}{{{f_{\max }} - {f_{{\rm{avg}}}}}}, \;\;f \ge {f_{{\rm{avg}}}}}\\ {{P_{{\rm{m}}1}}, \;\;f < {f_{{\rm{avg}}}}} \end{array}} \right.$ | (4) |
其中:fmax 为群体中最大的适应度值,favg为每代群体的平均适应度值,f′为要交叉的2个个体中较大的适应度值,f为要变异个体的适应度值,Pc1和Pc2为最大和最小交叉概率,Pm1和Pm2为最大和最小变异概率. 可以看出,当群体中各个个体的适应度趋于一致或趋于局部最优时,Pc和Pm增大,种群的多样性会提高,当群体的适应度值较为分散时,Pc和Pm减小. 因此,自适应操作既可以防止优良基因因为变异遭到破坏,又可以在陷入局部最优解时引入新的基因,在保持种群多样的同时,也保证了遗传算法的收敛性. 同时,在算法执行过程中,使用单方向进化逆转操作,进一步提高种群多样性,防止算法陷入局部最优解. 自适应遗传模拟退火算法计算正负残差点优化组合的具体步骤如下.
1) 设置遗传算法和模拟退火算法的各项控制参数,在这里对遗传算子和模拟退火算子不予赘述.
2) 编码,采用整数排列编码方式. 对预处理后的N个正负残差点均从1到N进行编码,将正残差点的排列建模为“主染色体”,作为各项操作的对象. 负残差点的排列为“参考染色体”,排列方式始终固定不变. 在2种染色体中,同一位置的基因对应图中匹配连接的一对正负残差点.
3) 种群初始化. 通过对“主染色体”进行随机排列,产生初始父代种群.
4) 适应度函数. 将“主染色体”对应的枝切线总长度fi的倒数作为适应度函数,即
| $a = \frac{1}{{\sum\limits_{i = 1}^N {{f_i}} }}$ | (5) |
5) 选择策略. 使用随机遍历抽样法. 相比于传统轮盘赌,可进一步提高选择的公平性.
6) 交叉操作. 将父代染色体随机两两分组,之后采用部分匹配交叉(PMX,partially matched crossover)算法完成对每组中2个父代染色体的交叉操作.
7) 变异操作. 通过互换染色体中任意2个位置的基因得到变异的子代染色体.
8) 单向进化逆转操作. 对染色体中的某一段基因进行逆转,计算逆转前和逆转后的染色体适应度值,保留适应度值较高的染色体.
9) 当种群完成步骤1)~8)操作后,依次对每个染色体执行模拟退火操作,具体步骤如下.
步骤1 产生新解. 交换当前染色体S1中任意2个位置的基因,产生新的染色体S2.
步骤2 Metropolis准则. 若S1和S2对应的枝切线总长度分别为f(S1)和f(S2),则2者长度差为
$ {\rm{d}}f = f({S_2}) - f({S_1}) $
使用Metropolis准则,有
| $P = \left\{ {\begin{array}{*{20}{l}} {1, \;\;{\rm{d}}f < 0}\\ {\exp \left( { - \frac{{{\rm{d}}f}}{{{T_0}}}} \right), \;\;{\rm{d}}f \ge 0} \end{array}} \right.$ | (6) |
如果df<0,则以概率1接受新的染色体S2,否则以概率exp(-df/T0)接受S2.
步骤3 降温. 当种群中所有“主染色体”执行完步骤1和步骤2后,进行降温操作. 若小于结束温度或达到最大遗传代数,则停止迭代,输出适应度最高的染色体,否则继续迭代.
得到最终输出的“主染色体”之后,将其与“参考染色体”对应起来,即可确定正负残差点对的组合方式. 之后,在干涉相位图中用枝切线连接所匹配的正负残差点,并根据干涉相位图生成相位导数方差质量图,从质量最好的点开始,使用洪水漫淹法(Flood-fill)绕开枝切线完成相位解缠.
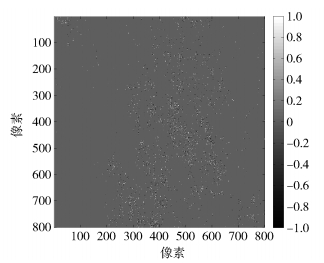
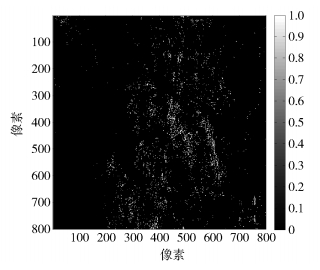
2 实验结果及分析实验中,对ER S-1/2获取的2幅Etna火山影像进行处理后得到800×800干涉相位,如图 1所示. 图 2为经4点环路积分法检测出的残差点图,其中正负残差点各3 819个. 使用Goldstein法和笔者所提方法设置的枝切线如图 3和图 4所示. 可以发现,Goldstein法在残差点密集处设置的枝切线很长,且存在非常多的重复连接的现象. 笔者所提方法通过预处理(距离阈值R=3)和后期优化,最终形成的枝切线都是许多独立的小“枝岔”,这样也就减少了无法进行解缠点的个数,同时也不会出现大面积的“孤岛”. 表 1给出了笔者所提方法和Goldstein法设置枝切线的时间、长度和封闭区域的量化对比.
| 表1 设置的枝切线长度、时间和封闭区域对比(运算环境:CPU为core i5-4200M,内存为4G) |
可以看出,笔者所提方法设置枝切线总长度比Goldstein法设置枝切线总长度减少7 161个像素,下降了40.5%,封闭区域数量下降了98.7%. 从运行时间上看,由于图像中心区域残差点分布较为密集,Goldstein法在设置枝切线时对大量残差点进行了重复连接,因此运行时间略长. 而笔者所提方法在预处理时,将大量距离较近的正负残差点进行了匹配,从而降低了后期优化算法的运行时间,提高了算法的整体运行速度. 因此,笔者所提方法在处理残差点过多的干涉相位图时,在枝切线的长度和运算时间上都要优于Goldstein枝切线法.
为了进一步验证笔者所提方法的有效性,分别对Goldstein枝切线法、笔者所提方法、质量图引导法和最小二乘法的解缠结果进行对比,并用算法总运行时间和解缠误差作为量化对比指标. 其中,解缠误差一般为
| $\begin{array}{l} \varepsilon = \frac{1}{{MN}}\sum\limits_{i = 1}^{M - 1} {\sum\limits_{j = 1}^N {\omega _{i, j}^x|{\phi _{i + 1, j}} - {\phi _{i, j}} - \Delta _{i, j}^x{|^p}} } + \\ \;\;\;\frac{1}{{MN}}\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^{N - 1} {\omega _{i, j}^y|{\phi _{i, j + 1}} - {\phi _{i, j}} - \Delta _{i, j}^x{|^p}} } \end{array}$ | (7) |
其中:${\omega _{i, j}^x}$和${\omega _{i, j}^y}$为缠绕相位梯度${\Delta _{i, j}^x}$和${\Delta _{i, j}^y}$对应的权重,一般从相位质量图导出,也可将权重忽略,即${\omega _{i, j}^x}$=${\omega _{i, j}^y}$=1. 笔者取${\omega _{i, j}^x}$=${\omega _{i, j}^y}$=1,并令p=0,即计算最小化解缠相位中的梯度与缠绕相位中的梯度不匹配的数目,也就是不连续点的数目,计算结果如表 2所示.
| 表2 解缠效果对比(运算环境:CPU为core i5-4200M,内存为4GB) |
图 5~图 8给出了上述4种算法的解缠结果. 从中可以看出,在残差点密集处,Goldstein法的解缠结果出现大面积“孤岛”,如图 5中的黑色区域所示. 最小二乘法的解缠相位图最为平滑,如图 8所示,运行时间也比较短,但作为一种全局算法,它将误差在相位图进行了扩散,可靠度较低,解缠误差远大于其他几种算法. 质量图引导法在解缠精度上有一定的优越性,但它对质量图的依赖较大,且在迭代过程中需要对纳入解缠队列中的元素按质量值的大小进行排序,因此运行时间远大于其他几种算法. 笔者所提方法得到的解缠结果如图 6所示,可以看出,枝切线整体较短,且没有形成大面积的封闭区域,解缠误差只略大于质量图引导法,但运行时间远小于质量图引导法. 相比Goldstein法,笔者所提方法的解缠误差和运行时间均有所降低. 因此,综合考虑解缠精度和运行时间,笔者所提方法具有一定的优越性.
3 结束语
在分析了Goldstein枝切线法不足之处的基础上,针对干涉相位图中残差点的分布特点,提出了一种将邻近偶极子对预处理和自适应遗传模拟退火算法相结合的相位解缠方法,用于生成许多极性平衡的小段枝切线. 最终不仅使枝切线整体长度较短,且有效地避免了大面积“孤岛”出现. 同时,可变距离阈值的预处理过程也保证了算法不会因残差点的数量过多而大幅降低执行效率. 对比实验结果表明,该方法兼顾了解缠精度和运行时间,是一种较为有效的相位解缠方法.
| [1] | Goldstein R M, Zebker H A, Werner C L. Satellite radar interferometry:two-dimensional phase unwrapping[J]. Radio Science, 1988, 23(4):713-720.[引用本文:1] |
| [2] | Huang Qian, Zhou Huiqun, Dong Shaochun, et al. Parallel branch-cut algorithm based on simulated annealing for large-scale phase unwrapping[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 3(7):3833-3834.[引用本文:1] |
| [3] | Ghiglia D C. Cellular-automata method for phase unwrapping[J]. Journal of the Optical Society of America, 1987, 1(4):267-280.[引用本文:1] |
| [4] | Dai Zhiyang, Zha Xianjie. An accurate phase unwrapping algorithm based on reliability sorting and residue mask[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 9(2):219-223.[引用本文:1] |
| [5] | 魏志强, 金亚秋. 基于蚁群算法的InSAR相位解缠算法[J]. 电子与信息学报, 2008, 30(3):518-523. Wei Zhiqiang, Jin Yaqiu. InSAR phase unwrapping algorithm based on ant colony algorithm[J]. Journal of Electronics and Information Technology, 2008, 30(3):518-523.[引用本文:1] |
| [6] | 曲小宁, 冯大政, 张妍, 等. TSP理论在二维相位解缠的应用[J]. 系统工程与电子技术, 2011, 33(4):742-745. Qu Xiaoning, Feng Dazheng, Zhang Yan, et al. TSP theory in the application of two-dimensional phase unwrapping[J]. Systems Engineering, and Electronics, 2011, 33(4):742-745.[引用本文:1] |
| [7] | 张妍, 冯大政, 曲小宁. 基于改进粒子群算法的二维相位解缠方法[J]. 电波科学学报, 2012, 27(6):1116-1123. Zhang Yan, Feng Dazheng, Qu Xiaoning. Two-dimensional phase unwrapping method based on improved particle swarm optimization[J]. Chinese Journal of Radio Science, 2012, 27(6):1116-1123.[引用本文:1] |
| [8] | Cusack R, Huntley J M. Improved noise-immune phase-unwrapping algorithm[J]. Applied Optics, 1995, 34(5):781-789.[引用本文:1] |