2. 鲁东大学数学与统计学院, 山东烟台 264025
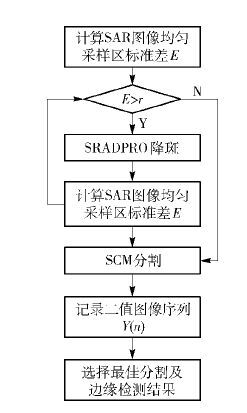
将改进后各向异性扩散相干斑抑制算法(SRADPRO)用于合成孔径雷达(SAR)图像相干斑抑制,并和脉冲发放皮层模型(SCM)结合,提出一种自适应SAR图像分割算法.该算法首先计算SAR图像均匀采样区的标准差,并以此评价SAR图像中相干斑的影响程度,进而自适应地决定是否采用SRADPRO进行降斑处理,然后再利用SCM进行图像分割.由于SCM的自动波扩散机理,使得该算法在获得分割后的SAR目标的同时,也得到了目标边缘检测结果.与多种常规算法的比较结果证明了SAR图像分割算法的有效性.
2. School of Mathematics and Statistics, Ludong University, Shandong Yantai 264025, China
An improved speckle reducing anisotropic diffusion (SRADPRO) algorithm was adopted to reduce the speckle in synthetic aperture radar (SAR) image. An adaptive SAR image segmentation algorithm speckle reducing spiking cortical model (SRSCM) was proposed when SRADPRO and spiking cortical model (SCM) was combined. In SRSCM, the standard deviation was calculated through a uniform sample region in the SAR image, and then the effect degree of speckle can be estimated as a result whether to employ the operator of SRADPRO was determined. At the second stage, the SCM operator was executed. Because of the auto wave characteristic of SCM, the segmented image and edge detection result can be obtained together. The effectiveness of SRSCM was proved by the comparisons with several traditional algorithms.
脉冲发放皮层模型(SCM,spiking cortical model)[1]是对脉冲耦合神经网络(PCNN,pulse coupled neural network)[2]模型的简化改进,具有和PCNN类似的同步脉冲发放特性,能较好地模拟视皮层神经元的工作特性。 目前,SCM模型已被应用到光学图像的特征提取、增强、分割、降噪等领域[3, 4],取得了优良的处理效果。
基于物理学领域的热传导过程或光顺理论而建立起来的一系列偏微分扩散方程模型[5, 6, 7],由于具有明确的物理含义和良好的处理效果,近年来被广泛应用到图像处理的降噪、分割、修复等领域。
由于特殊的成像机理,合成孔径雷达(SAR,synthetic aperture radar)图像中含有较强的相干斑噪声[8],若直接将光学图像处理中的一些经典算法用到SAR图像处理中,可能会失效。 笔者将SCM模型引入到SAR图像分割处理中,给出了SCM模型的适用条件,并结合各向异性偏微分扩散方程[5, 6],提出了一种自适应SAR图像分割算法(SRSCM,speckle reducing spiking cortical model),通过对不同类型SAR图像的处理,验证了SRSCM算法的有效性。
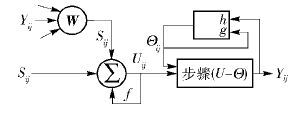
1 脉冲发放皮层模型SCM模型由哺乳动物初级视皮层神经元脉冲发放现象演化而来,比传统PCNN模型更简单,但仍具备了PCNN模型中生物电传输的指数衰减特性和视觉神经元神经系统的Gamma震荡特性,具有良好的生物学基础。 单个SCM神经元迭代可用式(1)~式(3)表示,SCM神经元模型结构如图 1所示. [1, 3, 4]。其中:Uij(n)为神经元(i,j)在网络运行中第n次迭代的内部活动项;Sij为神经元所受外部刺激,在图像处理应用中表示像素点(i,j)位置处的灰度值;Yij(n)为当前神经元脉冲输出状态,“1”表示神经元点火,有脉冲输出,“0”表示未点火;连接域突触连接权值矩阵Wijkl和Yij(n-1)的卷积表示邻域内神经元对中心神经元的影响程度;f,g分别为内部活动项Uij和阈值Θij的衰减系数,取值小于1;h为阈值Θij的放大系数,一般取值较大(如20),这样可使神经元发放一次脉冲后,阈值即获得较大提高,从而在后面较长一段时间内避免再次发放,此特性较好地模拟了生物神经元存在的不应期现象。
| \[{U_{ij}}\left( n \right) = f{U_{ij}}\left( {n - 1} \right) + Sij\sum\limits_{kl} {{W_{ijkl}}} {Y_{ij}}\left( {n - 1} \right) + {S_{ij}}\] | (1) |
| \[{\Theta _{ij}}(n) = (n - 1) + h{Y_{ij}}(n - 1)\] | (2) |
| \[{Y_{ij}}(n) = \left\{ {_{0}^{1{U_{ij}}(n) > {\Theta _{ij}}(n)}} \right.\] | (3) |
SCM模型能够用来进行图像分割,是由其具有脉冲同步发放特性决定的。 该特性是指,在SCM模型迭代过程中,灰度值较高的像素对应的神经元会自然激发,释放出的脉冲又会引起领域内灰度值相似的神经元的同步脉冲发放,从而使图像全局相似灰度值和局部相邻灰度值相似的像素点同步输出“1”,这样在神经元的输出端对Y进行记录,即可得到分割后的二值图像序列,从中挑选出分割效果较好的结果。
2 相干斑抑制算法SRADPRO偏微分方程(PDE,partial differential equations)方法近年来在图像处理领域得到了广泛应用,其去噪模型经过从线性扩散模型到非线性扩散模型、从各向同性扩散模型到各向异性扩散模型、从低阶扩散模型到高阶扩散模型的不同发展阶段,形成了系统的去噪理论[5, 6, 7]。 其中对于相干斑的抑制处理,Yu等[5]提出的各向异性扩散相干斑抑制算法(SRAD,speckle reducing anisotropic diffusion)首次将衡量相干斑抑制程度的等效视数用来构造扩散系数,不再采用幅度域图像的灰度确定扩散系数,这使该算法对相干斑的抑制效果有了大幅度提升。 但当迭代次数较大时,该算法仍会模糊图像的边缘和细节。 针对此问题,Yu等[6]进一步对扩散系数进行了改进。 笔者采用改进后各向异性扩散相干斑抑制算法(SRADPRO,speckle reducing anisotropic diffusion improve)。
采用PDE方法对灰度图像I0(x,y)进行降噪,可建模为对式(4)进行求解的过程[5, 6, 7]。
\[\left. {\begin{array}{*{20}{c}}
{\frac{{\partial I\left( {x,y;t} \right)}}{{\partial t}} = div\left[{c\left( {q\left( {x,y;t} \right)} \right)\nabla I\left( {x,y;t} \right)} \right]} \\
{I\left( {x,y,0} \right) = {I_0}\left( {x,y} \right),\left( {\frac{{\partial I\left( {x,y;t} \right)}}{{\partial n}}} \right)\left| {_{\partial \Omega } = 0} \right.}
\end{array}} \right\}\]
(4)
其中:div为散度;Δ为梯度;Ω和Ω分别为图像区域和图像边界;n为图像边界的外法线;I(x,y; t)为t时刻偏微分方程的迭代输出结果,其中(x,y)为像素的坐标;c(q(x,y; t))为扩散系数,不同降噪模型的区别主要体现在扩散系数的设计上。对微分方程式(4)进行离散化,假设Δt和h分别为足够小的时间和空间采样步长(取h=1,Δt=0.2),满足t=nΔt,n=0,1,…,x=ih,y=jh,i=0,1,…,M-1,j=0,1,…,N-1,其中图像大小为Mh×Nh,则式(4)中的连续图像I(x,y; t)可表示为I(ih,jh;nΔt),简写为Ii,jn,用di,jn表示c(·) ΔI的散度值,则式(4)的近似数值解可表示为[6]其中m为取中值函数。SRADPRO中的扩散系数由于采用了更准确的边缘检测算子式(8),所以算法在迭代降斑过程中更好地实现了对目标边缘和细节的保护。
| \[I_{i,j}^{n + 1} = I_{i,j}^n + \frac{1}{4}\Delta td_{i,j}^n\] | (5) |
| \[d_{i,j}^n = \frac{1}{{{h^2}}}\left[{c_{i + 1}^n - 1,j\left( {I_{j + 1,j}^n - I_{i,j}^n} \right) + c_{i,j}^n\left( {I_{i - i,j}^n - I_{i,j}^n} \right) + c_{i,j + 1}^n} \right.(I_{i,j + 1}^n - I_{i,j}^n) + c_{i,j}^n\left( {I_{i,j - 1}^n - I_{i,j}^n} \right)\] | (6) |
| \[c_{i,j}^n = \frac{1}{{1 + \left[{{{\left( {q_{i,j}^n} \right)}^2} - {q^2}0\left( n \right)} \right]/\left[{{q^2}0\left( n \right)\left( {1 + {q^2}0\left( n \right)} \right)} \right]}}\](7) | (7) |
| \[q_{i,j}^n = \frac{{{{\left| {\frac{1}{2}{{\left\| {\nabla I_{i,j}^n} \right\|}^2} - \frac{1}{{17}}{{\left[{{\nabla ^2}I_{i,j}^n} \right]}^2}} \right|}^{1/2}}}}{{\left[{I_{i,j}^n + \frac{1}{4}{\nabla ^2}I_{ij}^n} \right]}}\] | (8) |
| \[\left\| {\nabla I_{i,j}^n} \right\| = \frac{1}{{\sqrt 2 }}{\left( {{{\left\| {{\nabla _ + }I_{i,j}^n} \right\|}^2} + {{\left\| {{\nabla _ - }I_{i,j}^n} \right\|}^2}} \right)^{1/2}}\] | (9) |
| \[{\nabla _ \pm }I_{i,j}^n = \pm \frac{1}{h}\left[{I_{i \pm 1,j}^n - I_{i,j}^n,I_{i,j \pm 1}^n - I_{i,j}^n} \right]\] (10) | (10) |
| \[{\nabla ^2}I_{i,j}^n = \frac{1}{{{h^2}}}\left[{I_{i,j + 1}^n + I_{i,j - 1}^n + I_{i + 1,j}^n + I_{i - 1,j}^n - 4I_{i,j}^n} \right]\] | (11) |
| \[{q_0}\left( n \right) = 1.048m\left\{ {\left\| {\nabla \ln I - m\left[{\left\| {\nabla \ln I} \right\|} \right]} \right\|} \right\}\] | (12) |
由于相干斑的存在,使SCM模型直接用来对SAR图像进行分割在多数情况下不再适用。通过实验分析发现,只要相干斑影响足够小,则SCM模型仍可直接用来进行分割,否则需要先对SAR图像进行相干斑抑制处理。笔者采用SAR图像中均匀无目标区域的标准差来作为衡量SAR图像相干斑影响大小的指标,可表示为
\[E = \sqrt {\frac{1}{s}\sum\limits_{i = 1}^s {{{\left( {{x_i} - \mu } \right)}^2}} } \]
(13)
SRSCM分割算法的另一优点是,在输出二值图像序列中,最佳分割结果后面紧接着最佳边缘检测结果。因此,使用该算法可同时获得SAR图像目标分割和边缘检测结果,无须再额外施加任何边缘检测算子,这是由SCM自动波扩散的内在特性决定的。
4 实验结果首先列出了SRSCM算法对MSTAR库中运输车(zil131)、主战坦克(t72a64)和装甲运输车(btr60)在17°俯视角所成SAR图像的几组典型处理结果。 然后,又通过对某地区大范围海岛图片进行分割处理,进一步验证了SRSCM的有效性。
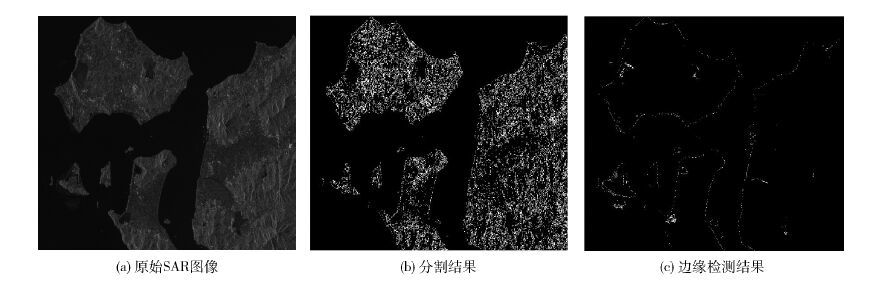
4.1 常见相干斑抑制算法与SCM模型结合后处理效果的对比图 3(a)和图 3(b)分别给出了运输车(zil131)的光学和SAR图像,从图 3中可以看出,2者特性差异很大。 为了证明SRSCM算法的有效性,图 3(c)~图 3(g)分别给出了SRAD[5]、DPAD[7]、PM扩散方程、Lee滤波器、Kuan滤波器与SCM模型结合的分割结果,图 3(h)和图 3(i)给出了SRSCM算法得到的分割和边缘检测结果。 通过对比可见,SRSCM模型分割最准确,并可同时得到目标边缘检测结果。
图 3(b)中的均匀无目标区域8×8采样窗口标准差E=0.1147,由SRSCM算法可知,此时需要首先进行降斑处理。采用SRADPRO进行相干斑抑制后的E=0.0339,此时仍有一定的残余相干斑,但影响已较小,图 3(h)和3(i)为SRSCM的最终处理结果。
4.2 SRSCM对其他类型SAR目标以及大范围SAR图像分割和边缘检测效果从图 4和图 5的实验结果可以看出,SRSCM算法对于MSTAR库中不同类型单目标的分割检测以及大范围多目标SAR图像的分割都是有效的。
5 结束语
综上,SRSCM算法是有效和实用的。 由于SRSCM输出的分割结果为二值图像,所以采用该算法对MSTAR库中SAR图像进行分割时,目标的阴影区域都被统一划到背景区域中。 若想保留阴影区域到分割结果中,则可通过对SCM模块进行扩充,使其能输出多级灰度值。
| [1] | Zhan Kun, Teng Jicai, Ma Yide. Spiking cortical model for rotation and scale invariant texture retrieval[J]. Journal of Information Hiding and Multimedia Signal Processing, 2013, 4(3): 155-165.[引用本文:2] |
| [2] | Wang Zhaobin, Ma Yide, Cheng Feiyan, et al. Review of pulse-coupled neural networks[J]. Image and Vision Computing, 2010, 28(1): 5-13.[引用本文:1] |
| [3] | 马义德, 滕飞, 绽琨, 等. 一种采用SCM模型的彩色图像增强方法[J]. 北京邮电大学学报, 2012, 35(3): 70-73.[引用本文:2] |
| [4] | Zhang Xuming, Li Liu, Zhu Fei, et al. Spiking cortical model-based nonlocal means method for speckle reduction in optical coherence tomography images[J]. Journal of Biomedical Optics, 2014, 19(6): 066005.[引用本文:2] |
| [5] | Yu Yongjian, Acton S T. Speckle reducing anisotropic diffusion[J]. Image Processing, IEEE Transactions on, 2002, 11(11): 1260-1270.[引用本文:5] |
| [6] | Yu Yongjian, Acton S T. Edge detection in ultrasound imagery using the instantaneous coefficient of variation[J]. Image Processing, IEEE Transactions on, 2004, 13(12): 1640-1655.[引用本文:6] |
| [7] | Aja-Fernández S, Alberola-López C. On the estimation of the coefficient of variation for anisotropic diffusion speckle filtering[J]. Image Processing, IEEE Transactions on, 2006, 15(9): 2694-2701.[引用本文:4] |
| [8] | Kou Guangjie, Wang Zhensong, Yao Ping. Multiple beams spaceborne SAR imaging[J]. Aerospace and Electronic Systems, IEEE Transactions on, 2012, 48(4): 3363-3375.[引用本文:1] |