提出了一种广义半迭代硬阈值追踪重建算法,综合了广义硬阈值追踪重建算法和半迭代思想的优点,修正了目标函数寻求最优解的搜索方向,获得了多项式的加速收敛,且不需要已知信号稀疏度.数值仿真结果表明,该算法在重构概率、峰值信噪比、信噪比、匹配度等方面的性能明显提高,且在"鬼"成像中的应用性能明显优于广义硬阈值追踪算法.
A recovery algorithm, named generalized semi-iterative hard thresholding pursuit, was proposed. The algorithm modifies the searching direction of objective function with semi-iterative idea, has a polynomial acceleration convergence, and can be used for the signal without sparse information. It is shown that the proposed algorithm did improve the performance in term of reconstruction probability, peak signal-to-noise ratio, signal-to-noise ratio, and matching rate. The reconstruction quality in ghost imaging with the proposed algorithm is superior to that with the generalized hard thresholding method.
压缩感知(CS,compressed sensing)技术[1]将数据采集和压缩合二为一,极大地提高了资源利用率和信号处理效率,也在量子光学的最新领域——“鬼”成像方面得到应用[2],其中重构算法是CS技术的关键. 广义硬阈值追踪(GHTP,generalized hard thresholding pursuit)算法[3]包含匹配追踪算法[4]和迭代硬阈值算法[5]的特点,且不需要已知信号稀疏度. 但算法中硬阈值函数的迭代为最速下降法,需要多次迭代才能获得最优解. 另外,半迭代思想可实现迭代类算法中的多项式加速[6]. 因此,笔者综合广义硬阈值追踪算法和半迭代思想的优点,提出了一种广义半迭代硬阈值追踪(GSHTP,generalized semi-iterative hard thresholding pursuit)重建算法. 通过数值计算分析了GSHTP算法在重构概率、信噪比和峰值信噪比等方面的性能,以及在“鬼”成像中的应用.
1 广义半迭代硬阈值追踪算法
CS的一般求解模型为
min ‖ x ‖0 s.t. y=Φx
(1)
min${1 \over 2}$‖ y-Φx ‖22 s.t.‖ x ‖0≤K
(2)
x n=HK( x n-1+α Φ T( y-Φx n-1))
(3)
式(3)表明,在GHTP算法迭代更新时,沿着负梯度方向来搜索最优解. 因此,需要多次迭代才能获得最优解. 为了克服上述困难,现引入半迭代思想来加速多项式收敛. 将式(1)等价表示为
x=Gx+h
(4)
V n=μ0,n x n+μ1,n x n-1+…+μn,n x 0
(5)
x n=Hs( V n-1+ωn Φ T( y - Φ x n-1))
(6)
通过半迭代方法,GSHTP算法将选取的s列原子(测量矩阵 Φ 的列)按照斯密特正交化的方法进行正交投影,保证了已选的原子张成的空间和残差空间是正交的,一旦选定,在后面的迭代中不再选取,从而减少了迭代次数,通过反复迭代,自适应地估计信号的真实稀疏度,不需要原始信号的先验知识.
定理1 若 x n→ x *(最优解),必存在V n→x *;当 x n不收敛时,V n仍有可能收敛,且V n收敛到式(4)的充要条件为 G 的谱半径小于1,即ρ( G )<1.
证明 通过半迭代方法来搜索方程 x n= G x n-1+ h 的最优解,x *满足x *= Gx *+ h .
令V n=$\sum\limits_{i = 0}^n {{\mu _{i,n}}} {x^i}$,其中$\sum\limits_{i = 0}^n {{\mu _{i,n}}} = 1$,定义 ε n= x n-x *,η n=V n-x *,由于 V 0= x 0,故 ε 0= η 0,且 ε i= Gε i-1=…= G i ε 0,则 \[\eqalign{ & \sum\limits_{i = 0}^{n - 1} {{\mu _{i,n - 1}}} {x^i},\sum\limits_{i = 0}^{n - 1} {{\mu _{i,n - 1}}} = 1, \cr & \sum\limits_{i = 0}^n {{\mu _{i,n}}} {x^i},\sum\limits_{i = 0}^n {{\mu _{i,n}}} = 1, \cr & {\eta ^n} = \sum\limits_{i = 0}^n {{\mu _{i,n}}} {x^i} - \sum\limits_{i = 0}^n {{\mu _{i,n}}} {x^*} = \cr & \sum\limits_{i = 0}^n {{\mu _{i,n}}} {\varepsilon ^i} = \left( {\sum\limits_{i = 0}^n {{\mu _{i,n}}} {G^i}} \right){\varepsilon ^0} = \cr & {P_n}\left( G \right){\varepsilon ^0} = {P_n}\left( G \right){\eta ^0} \cr} \] 其中: P n( G )=${\sum\limits_{i = 0}^n {{\mu _{i,n}}} {G^i}}$,P n(1)=1,设迭代矩阵 G 的特征值为λ1,λ2,…,λi,则 P n( G )的特征值为 P n(λi),i=1,2,…,谱半径为ρ( P n( G ))=$\mathop {\max }\limits_i $| P n(λi)|,又因为ρ( P n( G ))<1,则 η n= P n( G ) η 0→0,即V n=$\sum\limits_{i = 0}^n {{\mu _{i,n}}} {x^i}$→x *,得V n收敛到式(4)的解,证毕.
定理2 式(5)的迭代关系确保了迭代方向与前一次的梯度下降方向不正交.
证明 设罚函数表达式为
f( x )=(1/2)‖ y - Φ x ‖22
通过求导可得其梯度方向为
▽ f( x )=((1/2)‖ y - Φ x ‖22)′= Φ T( Φ x-y )
已知最速下降法的迭代公式为
x n+1= x n-α ▽ f( x n)= x n-α ▽ fn
f( x n-α ▽ fn)=$\mathop {\max }\limits_{\alpha > 0} $f( x n-α ▽ fn)
为了求解最优化问题$\mathop {\max }\limits_{\alpha > 0} $ f( x n-α ▽ fn),令$\phi $(α)= f( x n-α ▽ fn),则
$\phi $′(α)=f'( x n-α ▽ fn)=
▽ fnT f( x n-α ▽ fn)=
▽ fnT ▽ fn+1=0
已知 ▽ f( x n)= Φ T( Φx n- y ),通过半迭代方法,有
V n+1=μ0,n+1 x n+1+μ1,n+1 x n+…+μn+1,n+1 x 0
▽ f( V n+1)= Φ T( Φ V n+1- y )=
Φ T( Φ (μ0,n+1 x n+1+…+μn+1,n+1 x 0)- y )
相乘可得 ▽ f( x n)T ▽ f( V n+1)≠0,定理2得证.
因此,GSHTP算法的具体步骤描述如下.
输入:测量矩阵 Φ ∈ R M×N,测量值 y ∈ R M,每次迭代时的索引步长N0.
输出:重构信号${{\hat x}^k}$,索引集Γk.
初始化:残差 r 0= y ,索引集Γ0=φ,外循环迭代次数k=0,重构信号 x 0= x 0.
步骤1 k=k+1,计算索引值s=N0k,内循环迭代次数n=1;
步骤2 采用半迭代方法选取s个原子,有
x n=Hs( V n-1+ωn Φ T( y - Φ x n-1))
更新原子索引集Sn=sup ( x n);
步骤3 采用最小二乘法进行正交投影,有
x n=arg min z ‖ y - Φ z ‖2
s.t. sup ( z )$ \subseteq $Sn
更新残差 r n= y - Φ x n;
步骤4 判断是否满足‖ r n‖2≥‖ r n-1‖2,若满足,执行步骤1;否则n=n+1,执行步骤2;
步骤5 更新重构信号 ${{\hat x}^k}$ = x n,支撑集Γk=Sn,残差 ${{\hat x}^k}$ = r n;
步骤6 判断是否满足‖ x n- x n-1‖< ε ,若满足,执行步骤7;否则,执行步骤1;
步骤7 输出重构信号 ${{\hat x}^k}$ ,索引集Γk.
在上述步骤中,外循环用来估计稀疏度,以变量k为标志,在第k次估计时,增加s=N0k个索引值,直到当前的信号能量与上一次的信号能量差小于某个很小的阈值 ε (如10-5),说明s能满足当前重建信号的要求,则变量k不再更新,输出重构信号;内循环用来重构信号,以变量n为标志,通过非线性操作Hs( ·),每次选择s个原子加入信号支撑集中. 如果当前的残差能量大于上一次的残差能量,则跳出内循环,否则更新变量n,继续搜索最优解.
改进的GSHTP算法由于采用了半迭代的思想修正目标函数的搜索方向,需要前n次迭代值的线性加权之和,其计算复杂度为O(kn2),较之GHTP算法中的硬阈值函数(采用最速下降法,其计算复杂度为O(kn))有所增加.
2 数据仿真及结果分析下面通过数值仿真验证所提算法的有效性. 数值仿真在Matlab R2010a处理平台上进行,计算机型号为Thinkpad SL400,处理器为Inter Core 2,内存大小为2 GB. 重构概率、信噪比等结果均为1万次的平均值.
在GSHTP算法迭代更新公式中,需要前n次迭代值的线性加权之和,这对矩阵的动态存储要求很高. Hanke[7]给出的半迭代方法可通过2步迭代过程来有效完成,在提高重构性能的同时,有效地保证了计算复杂度与原有算法相同,为O(kn). 因此,在数值仿真时,采取第n-1和n-2项来进行搜索方向的修正,即迭代更新关系为
$\left. \matrix{
{x^n} = {H_s}\left( {{V^{n - 1}} + {\omega _n}{\Phi ^{\rm{T}}}\left( {y - \Phi {x^{n - 1}}} \right)} \right) \hfill \cr
{V^{n - 1}} = {\mu _n}{x^{n - 1}} + \left( {1 - {\mu _n}} \right){x^{n - 2}} \hfill \cr} \right\}$
(7)
${\mu _n} = {{1 + \left( {n - 1} \right)\left( {2n - 3} \right)\left( {2n + 2c - 1} \right)} \over {\left( {n + 2c - 1} \right)\left( {2n + 4c - 1} \right)\left( {2n + 2c - 3} \right)}}$
当然,随着c的取值不同,算法的重构概率会发生改变.
1) 参数c的确定
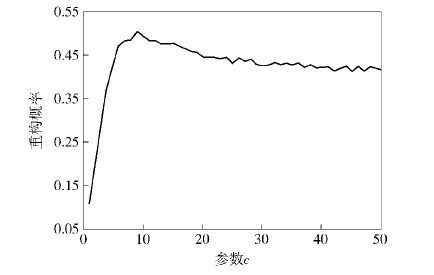
为了更好地获得重构概率,图 1给出了GSHTP算法在恢复1维信号时,重构概率随着参数c不同取值的变化曲线. 其中:原始信号 x 的长度为N=256,稀疏度为K=64,索引值为N0=4,测量值 y 的长度为M=128,测量矩阵 Φ 为M×N维的高斯随机矩阵,在算法迭代停止时采用的阈值为 ε =10-5,c的取值范围为{1,2,…,49,50}.
图 1显示了当参数c∈(1,9)时,重构概率呈指数增加,且当c=9时,重构概率达到最大值0.5;当c∈(9,50)时,重构概率呈下降趋势,并趋于稳定. 因此,GSHTP算法的重构性能在c=9时最好,以下数值仿真中都将c设为9.
2) 重构概率曲线
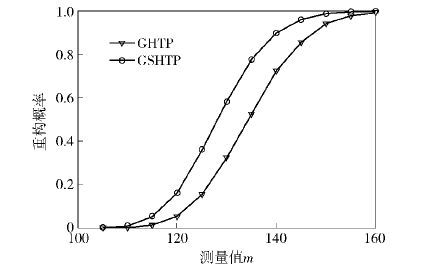
图 2给出了随着观测次数m的不同,GSHTP算法和GHTP算法重构概率的变化曲线. 其中:随机生成的1维信号 x 的长度为N=256,稀疏度为K=64,索引值为N0=4,参数为c=9,测量值 y 的长度为m,测量矩阵 Φ 为m×N维的高斯随机矩阵,由于m<105时的重构概率恒为0,而m>160时的重构概率恒为1,因此m的取值范围为{105,110,…,155,160}.
图 2结果表明,随着观测信号值的逐步增加,2种算法的重构成功概率也从0增大到1. 但GSHTP算法的重构概率曲线始终位于GHTP算法的上方,即在同等条件下,GSHTP算法比GHTP算法具有更优的重构性能.
3) 信噪比、匹配度性能比较
为了进一步说明GSHTP算法的重构性能,表1列出在压缩比均为M/N=128/256,对256×256的Lena图像进行重构时,各种重建算法在峰值信噪比、信噪比、匹配度等方面的性能. 结果表明,GSHTP算法在峰值信噪比、信噪比、匹配度等方面均优于匹配追踪、迭代硬阈值、硬阈值追踪和GHTP等算法. 与GHTP算法相比,在压缩比为0.5时,GSHTP算法的峰值信噪比提高了0.4 dB,信噪比提高了1 dB,匹配度增加了0.2%. 其中:峰值信噪比定义为
$Q = 10\lg \left( {{{{{\left( {{2^D} - 1} \right)}^2}} \over {\sigma \left( {x - \hat x} \right)/a/b}}} \right)$
(8)
信噪比定义为
$\delta = 20\lg \left( {{{\sigma \left( x \right)} \over {\sigma \left( {x - \hat x} \right)}}} \right)$
(9)
匹配度定义为
$\beta = 1 - {{\sigma \left( {\left| {\hat x} \right| - \left| x \right|} \right)} \over {\sigma \left( {\left| {\hat x} \right| + \left| x \right|} \right)}}$
(10)
| 表1 5种算法的重建性能对比 |
“鬼”成像(GI,ghost imaging)是量子光学领域的前沿和热点,能在没有物体的参考光路获得物体的清晰图像,可突破经典衍射极限,具有高分辨率和高可见度. 压缩“鬼”成像(CGI,compressed ghost imaing)利用CS重建算法,极大地提高了成像质量,减少了成像时间[8]. 为了验证所提重建算法在“鬼”成像中的应用性能,笔者进一步考虑基于GSHTP算法的CGI质量. 仿真时的目标物体设为128×128像素的二灰度“NUPT”图和八灰度“boat”图. GI采样次数为10 000次,CGI采样次数为500次,重构算法分别为GHTP算法和GSHTP算法,数值仿真结果如图 3所示.
图 3(a)和图 3(b)分别为二灰度“NUPT”恢复图和八灰度“boat”恢复图的对比. 结果表明,在采样次数远远小于GI的情况下,CGI的恢复质量明显好于GI;在重构二灰度“NUPT”图时,GHTP算法的峰值信噪比为Q=19.6 dB,而GSHTP算法的峰值信噪比为Q=22.8 dB,提高了3.2 dB.
4 结束语综合了广义硬阈值追踪算法和半迭代方法的优点,提出了一种广义半迭代硬阈值追踪压缩感知(GSHTPCS,generalized semi-iterative hard thresholding pursuit compressed sensing)重建算法,该算法在不需要信号先验稀疏度的情形下,迭代中的最优解搜索方向为当前的负梯度方向和前多次的搜索解元素之差的线性组合,有效地避免了因单一的负梯度方向产生的锯齿效应,收敛速度得到多项式加速. 数值计算结果表明,GSHTP算法在峰值信噪比Q、信噪比δ、匹配度β等方面均优于匹配追踪、迭代硬阈值、硬阈值追踪和GHTP等算法;与GHTP算法相比,在信号稀疏度未知的前提下,GSHTP算法的重构效率也得到了明显提升;在对二灰度“NUPT”图和八灰度“boat”图的压缩关联重建时,成像质量和成像时间等性能明显优于GHTP算法.
| [1] | Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4):1289-1306.[引用本文:1] |
| [2] | 白旭, 李永强, 赵生妹. 基于压缩感知的差分关联成像方案研究[J]. 物理学报, 2013, 62(4):044209. Bai Xu, Li Yongqiang, Zhao Shengmei. Differential compressive correlated imaging[J]. Acta Phys Sin, 2013, 62(4):044209.[引用本文:1] |
| [3] | Li Haifeng, Fu Yuli, Zhang Qiheng, et al. A generalized hard thresholding pursuit algorithm[J]. Circuits Systems and Signal Processing, 2013, 33(4):1313-1323.[引用本文:1] |
| [4] | Needell D, Tropp J A. CoSaMP:iterative signal recovery from incomplete and inaccurate samples[J]. Applied and Computational Harmonic Analysis, 2009, 26(3):301-321.[引用本文:1] |
| [5] | Blumensath T, Davies M E. Iterative hard thresholding for compressed sensing[J]. Applied and Computational Harmonic Analysis, 2009, 27(3):265-274.[引用本文:1] |
| [6] | Zhou Xueqin, Feng Xiangchu, Jing Mingli. Sparse recovery by semi-iterative hard thresholding algorithm[J]. Mathematical Problems in Engineering, 2013, 2013:1-6.[引用本文:1] |
| [7] | Hanke M. Accelerated landweber iterations for the solution of ill-posed equations[J]. Numerische Mathematik, 1991, 60(1):341-373.[引用本文:1] |
| [8] | Katz O, Bromberg Y, Silberberg Y. Compressive ghost imaging[J]. Applied Physics Letters, 2009, 95(13):131110.[引用本文:1] |