针对数据中心的计算节点建立精密的能耗模型来预测能耗状况很有必要.为了解决线性模型准确性不足的问题,提出了一种基于分段式CPU利用率的能耗模型,并且加入了内存和硬盘因素.在实验中发现了其他部件的耗能与CPU的内在联系,给出了潜在影响公式.随后,在单机环境和并行环境下验证了模型的准确性.
With development of cloud computing and big data, the energy consumption of data center becomes more and more serious. It is necessary to establish a precise model of energy consumption for the computing node of the data center. In the most previous studies, linear system utilization is taken to establish the models of energy consumption. In order to solve the accuracy insufficient of linear model, a model of energy consumption based on the segmented CPU utilization was proposed when considering the memory and the hard drive at the same time. In the experiment, the inner relationship between the energy consumption and the CPU was found, and a formula of the potential influence of the components was proposed, and the accuracy of the model is verified in both single environment and parallel environment.
云计算是一种高效、合理的计算节点管理模式,但并无有效的方案来降低能耗,仍需研究合理的任务模式实现绿色计算[1, 2]. 并要实时准确地反映各节点的能耗变化. 采用硬件方式实时监测数据中心中每个节点的能耗情况,工作量巨大,成本也很高[3, 4]. 因此,研究准确性高的能耗模型非常重要.
笔者试图从云平台基础设施层面为数据中心的服务器建立合理、可靠的能耗模型. 对于影响能耗模型的因素(CPU、内存利用率与I/O读写等),找出各部件影响能耗的因子,设计能耗模型,达到准确检测能耗的目的.
1 相关工作基于系统利用率的能耗模型就是对各个部件建 立相应的能耗模型,生成节点的能耗模型. 在计算节点能耗模型的建立过程中,一般遵循以下3个原则[5].
1) 准确性高. 只有准确性高的能耗模型才能精确地反映能耗的变化,有利于节能算法的设计.
2) 通用性强. 适用于不同品牌、型号的服务器.
3) 可移植性高. 各种大小、种类的集群都能准确地预测能耗.
笔者在现有研究的基础上充分考虑了影响能耗产生的所有部件(CPU、内存和硬盘)[6],通过线性回归算法建立了准确性较高的三元线性模型,并分析了(CPU,内存)和(CPU,硬盘)之间内在的联系,设计出最终的非线性能耗模型[7]. 最后通过实验分析了线性模型和非线性模型的准确性,并设计了不同场景下的实验来检测模型的准确性.
2 非线性能耗模型的建模过程根据之前的研究表明,CPU和内存是计算节点产生能耗的两个部件,占了整体能耗的80%~90%;硬盘和网络负载也占有一定比例,尤其当产生大量的I/O操作时,硬盘产生的能耗会迅速提高. 笔者采集了CPU利用率Uc、内存利用率Um、硬盘利用率(CPU用于I/O读写的利用率)UI/O以及实时功率P. {Uc,Um,UI/O}构成一个三元组模拟实时功率P,并以此为基础深入分析了CPU利用率、内存利用率和硬盘利用率对产生能耗的内部联系,构建非线性模型模拟能耗的产生.
2.1 CPU能耗模型
以往研究中,基于CPU利用率的线性能耗模型是最常用的模型. 典型的单线式CPU利用率能耗模型的表达式为
Pc=γcUc+γ0
(1)
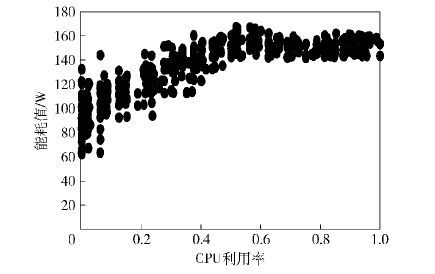
通过对图 1的分析得知,能耗与CPU利用率的关系不是简单的线性关系,在CPU利用率50%附近发生了变化,呈分段式的线性分布. 因此,把CPU能耗模型从简单的单线式线性模型变成了分段式线性模型:
${P_c}{\rm{ = }}\left\{ \matrix{
\gamma _{\rm{c}}^1{U_{\rm{c}}} + \gamma _{\rm{0}}^1, {U_{\rm{c}}} \le 0.5 \hfill \cr
\gamma _{\rm{c}}^2{U_{\rm{c}}} + \gamma _{\rm{0}}^2, {U_{\rm{c}}} > 0.5 \hfill \cr} \right.$
(2)
内存是除了处理器之外耗能最多的部件. 在之前的模型研究中,大多数学者认为能耗与内存利用率是呈线性相关的,如式(3)所示.
Pm=γmUm+γ0
(3)
Pm=f(Uc)Um+γ0
(4)
硬盘也是计算节点一个重要能耗部件. 采用较易采集的硬盘利用率UI/O模拟硬盘能耗,硬盘利用率UI/O指CPU用于I/O读写的利用率. 于是,设计了线性模型式(5)和非线性模型式(6)来表示硬盘能耗.
PI/O=γI/OUI/O+γ0
(5)
PI/O=γI/OUcUI/O+γ0
(6)
联合式(1)、式(3)和式(5)得到单线式线性能耗模型modleliner_single(见式(7)),联合式(2)、式(3)和式(5)得到分段式线性能耗模型modleliner_segment(见式(8)).
Pt=γcUc+γmUm+γI/OUI/O+γ0
(7)
${P_{\rm{t}}}{\rm{ = }}\left\{ \matrix{
\gamma _{\rm{c}}^1{U_{\rm{c}}} + \gamma _{\rm{m}}^1{U_{\rm{m}}} + {\gamma _{{\rm{I}}/{\rm{O}}}}{U_{{\rm{I}}/{\rm{O}}}} + \gamma _{\rm{0}}^1, {U_{\rm{c}}} \le 0.5 \hfill \cr
\gamma _{\rm{c}}^2{U_{\rm{c}}} + \gamma _{\rm{m}}^2{U_{\rm{m}}} + {\gamma _{{\rm{I}}/{\rm{O}}}}{U_{{\rm{I}}/{\rm{O}}}} + \gamma _{\rm{0}}^2,{U_{\rm{c}}} > 0.5 \hfill \cr} \right.$
(8)
联合式(1)、式(4)和式(6)得到单线式非线性能耗模型modlenoliner_single(见式(9)),联合式(2)、式(4)和式(6)得到分段式非线性能耗模型modlenoliner_segment(见式(10)).
Pt=γcUc+f(Uc)Um+γI/OUcUI/O+γ0
(9)
${P_{\rm{t}}}{\rm{ = }}\left\{ \matrix{
\gamma _{\rm{c}}^1{U_{\rm{c}}} + f\left( {{U_{\rm{c}}}} \right){U_{\rm{m}}} + {\gamma _{{\rm{I}}/{\rm{O}}}}{U_{\rm{c}}}{U_{{\rm{I}}/{\rm{O}}}} + \gamma _{\rm{0}}^1, {U_{\rm{c}}} \le 0.5 \hfill \cr
\gamma _{\rm{c}}^2{U_{\rm{c}}} + f\left( {{U_{\rm{c}}}} \right){U_{\rm{m}}} + {\gamma _{{\rm{I}}/{\rm{O}}}}{U_{\rm{c}}}{U_{{\rm{I}}/{\rm{O}}}} + \gamma _{\rm{0}}^2,{U_{\rm{c}}} > 0.5 \hfill \cr} \right.$
(10)
根据第2节中的论述,测量计算节点的能耗需要采集CPU利用率、内存利用率与硬盘利用率以及通过3种不同类型的并行算法来检验模型的可移植性. 本组实验的实验环境如表1所示.
| 表1 实验环境描述 |
单线式线性能耗模型modleliner_single(见式(7))经过线性回归算法分析之后,得出各影响因子的数值. 其中,γc的数值为66.256 13,γm的数值为19.408 09,γI/O的数值 为8.143 29,γ0的数值为94.918 38.
3.2.2 分段式线性能耗模型分段式线性能耗模型modleliner_segment(见式(8)),经过线性回归算法分析之后,得出各影响因子的数值. 其中,γc1的数值为132.475 81,γm1的数值为28.090 61,γI/O 的数值为8.847 54,γ01的数值为78.283 68;γc2的数值为-7.799 79,γm2的数值为13.740 60,γ02的数值为150.569 95.
3.2.3 单线式非线性能耗模型单线式非线性能耗模型modlenoliner_single(见式(9))经过回归算法分析之后,得出各参数的数值与表达式. 其中,γc的数值为66.256 13,f(Uc)为(1-ln(Uc))/3.119 39,γI/O的数值为8.143 29,γ0的数值为94.918 38.
3.2.4 分段式非线性能耗模型分段式非线性能耗模型modlenoliner_segment(见式(10)),经过回归算法分析之后,得出各参数的数值与表达式. 其中,γc1的数值为132.475 81,f(Uc)为(1-ln(Uc))/3.119 39,γI/O的数值为8.847 54,γ01的数值为78.283 68;γc2的数值为-7.799 79,γ02的数值为150.569 95.
3.3 实验结果分析实验1 单线式和分段式的准确性比较
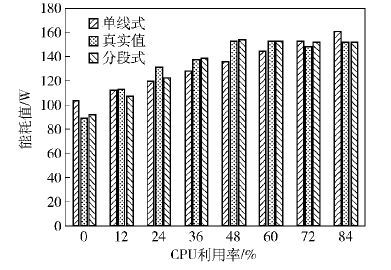
通过图 1的直观展示,判断分段式能耗模型的准确性优于单线式的能耗模型. 下面通过实验来证明这个结论. 实验将CPU利用率以12%为增长幅度,数据集的真实能耗取平均值,如图 2所示.
通过图 2可以看出,在CPU利用率的各个阶段,分段式模型都有良好的准确性表现,整体准确性也优于单线式.
实验2 各个最终能耗模型的准确性比较
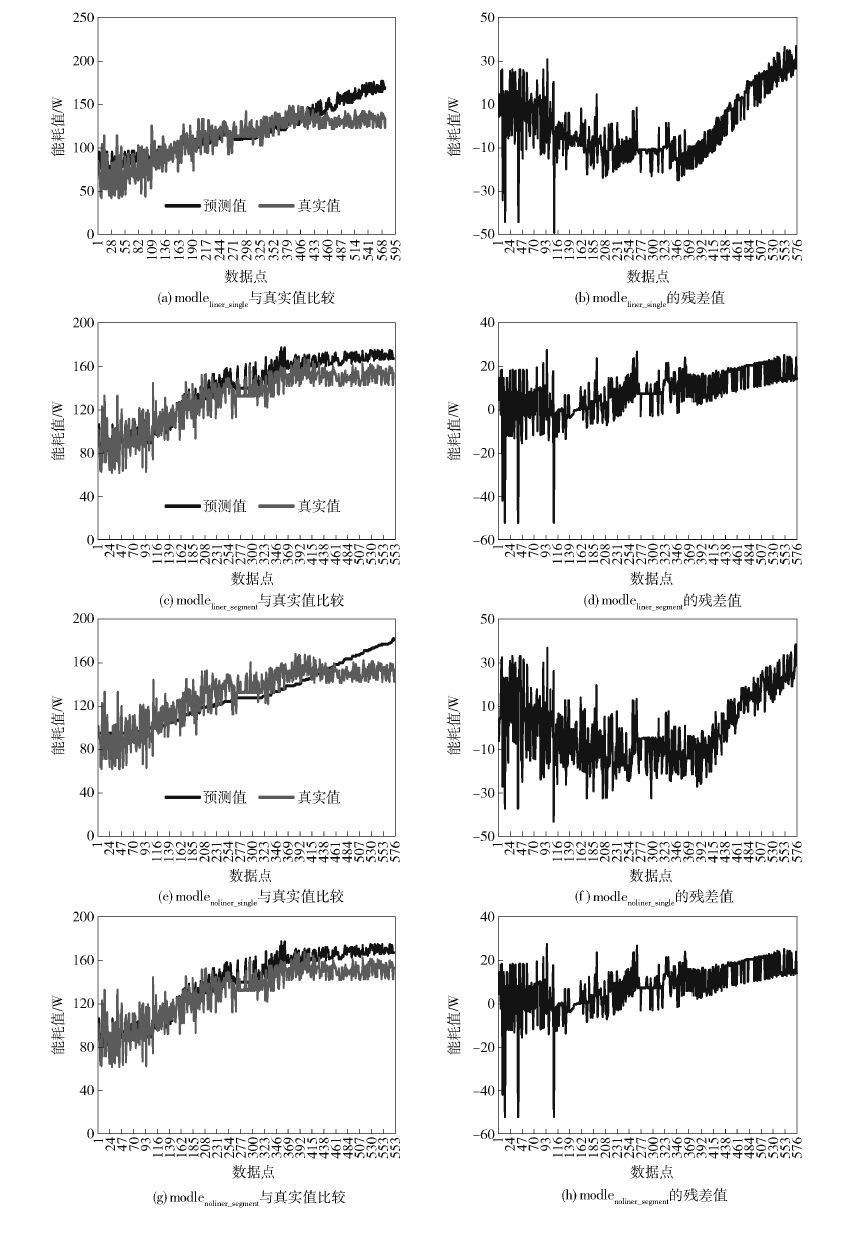
实验将比较式(7)~式(10)的模型准确性表现,并比较每个数据点的模型预测值和真实值的残差值,以计算准确性,如图 3所示.
分别计算了各模型的残差总和及准确率,如表2所示.
| 表2 各模型残差和与准确率 |
通过图 3和表2验证了之前的推测,即单线式线性能耗模型准确性最低,分段式非线性能耗模型准确性最高.
实验3 各模型在真实场景下的表现
选取SPEC2006作为真实场景的模拟工具. SPEC2006是一个评估CPU和内存性能的工具. 真实场景中各算法能耗真实值和预测值的比较,如图 4所示.
从图 4 中可以看出各模型整体表现不错,其中分段式非线性能耗模型准确性最高.
实验4 云计算环境下各模型表现
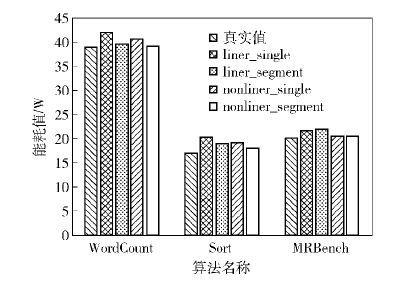
为了验证能耗模型的可移植性,选取3种不同类型的并行算法作为云计算实例. 在上述的云计算环境中选取了1 GB大小的数据集来采集3种算法的数据,比较算法能耗的真实值和预测值,如图 5所示.
通过图 5可以得知各模型在云计算环境下表现不错,单机环境下的结论在云计算环境下也得到了验证. 分段式非线性能耗模型依然是表现最好的.
4 结束语通过对单机环境下系统利用率和能耗的分析,发现了CPU利用率呈分段式的线性分布,进而发现了内存产生能耗时与CPU的内在联系,得出CPU与内存的影响公式,并且加入了硬盘形成了最终的能耗模型. 模型在单机环境、真实场景与并行环境的实验中,准确性表现稳定.
在以后的研究中,拟将所提能耗模型与节能措施联系起来,针对不同系统利用率的任务提出相应的节能手段,从而达到节能的目的.
| [1] | Fan X, Weber W D, Barroso L A. Power provisioning for a warehouse-sized computer[J]. ACM SIGARCH Computer Architecture News, 2007, 35(2):13-23.[引用本文:1] |
| [2] | Elnozahy E N, Kistler M, Rajamony R. Energy-efficient server clusters[C]//Falsafi B, Vijaykumar T N. Proc. of the 2nd Int'l Workshop on Power-Aware Computer Systems (PACS 2002). Cambridge:Springer-Verlag, 2003. 179-197.[引用本文:1] |
| [3] | Song Jie, Li Tiantian, Yan Zhenxing, et al. Energy-efficiency model and measuring approach for cloud computing[J]. Journal of Software, 2012, 23(2):200-214.[引用本文:1] |
| [4] | Aman Kansal, Zhao Feng, Liu Jie, et al. Virtual machine power metering and provisioning[C]//Proceedings of the 1st ACM Symposium on Cloud Computing, SoCC'10, 2010. Indianapolis, IN, United states:Association for Computing Machinery, 2010:39-50.[引用本文:1] |
| [5] | Bohra, Ata E Husain, Chaudhary Vipin. VMeter:power modelling for virtualized clouds[C]//Proceedings of the 2010 IEEE International Symposium on Parallel and Distributed Processing, Workshops and Phd Forum, IPDPSW 2010. Atlanta, GA, United states:IEEE Computer Society, 2010:1-8.[引用本文:1] |
| [6] | Tan Yiming, Zeng Guosun, Wang Wei. Policy of energy optimal management for cloud computing platform with stochastic tasks[J]. Journal of Software, 2012, 23(2):266-278.[引用本文:1] |
| [7] | Luo Liang, Wu Wenjun, Zhang Fei. Energy modeling based on cloud data center[J]. Journal of Software, 2014, 25(7):1371-1387.[引用本文:1] |