2. 苏州大学江苏省计算机信息处理技术重点实验室, 江苏苏州 215006
设计并实现了一种面向能耗均衡的传感网单移动sink数据收集方法.利用传感网完全覆盖模型确定了sink在网内各遍历点的具体坐标,并在此基础上,构建了其定长移动数据收集轨迹.实验结果表明,该方法的能耗均衡性优于虚拟节点策略、基于效用的贪婪启发式交会点找寻等典型的移动sink数据收集方法.
2. Provincial Key Laboratory for Computer Information Processing Technology, Soochow University, Jiangsu Suzhou 215006, China
A type of data gathering method based on one mobile sink for balanced energy consumption in sensor networks (DGBEC) was proposed. Coordinates of each traverse point was calculated by sensing coverage model, and the path with fixed length for mobile sink was also built. Simulations show that DGBEC performs very well in energy consumption balance than virtual nodes priority (VNP) and rendezvous points finding with a utility-based greedy heuristic (RP-UG) methods.
当前,基于移动sink节点的数据收集模式逐渐成为研究的热点[1, 2, 3]. 通过随机或固定的移动轨迹,使sink节点最大可能地靠近数据收集点,不仅提升了数据收集效率和可靠性,避免了多跳、多径路由带来的能耗开销,而且可有效避免数据收集过程中的“热区”现象的出现[4]. 然而,面对复杂多变的拓扑,如何针对移动sink节点进一步开展合理的移动路径规划,如何在数据收集过程中实现节点的休眠调度,如何尽可能确保数据收集节点的能耗均衡性,是该领域亟须解决的主要问题.
1 研究背景Sink的移动方式主要分为随机、固定和可控等3种. 在随机移动模型方面,Konstantopoulos等[2]提出了一种Data MULEs方法来收集稀疏静态部署的数据,利用可随机移动的代理节点,依次访问各数据收集点;Anastasi等[3]则首次将该架构应用于真实的城市环境感知场景,分析了sink的移动速度、sink与数据收集点间距等因素对收集性能的影响. 在固定轨迹的sink移动方面,Chakrabarti等[4]提出可预测sink移动性概念以提高网络性能,但要求所有节点都分布在sink直接通信范围;Liang等[5]分析了稀疏传感网络下移动sink数据收集和能耗之间的权衡关系,但仍仅能采用单跳通信方式. 可控的sink移动模型则根据网络实时热区和数据收集节点的反馈信息,对后续运动轨迹进行预判,提升了数据收集效率[4]. Somasundara等[6]提出了2种启发式算法获得近似优化的移动路径,但该方法易造成移动sink在相距较远的节点之间往复移动;Gao等[7]设计了一种基于虚拟点优先级的sink移动轨迹优化选择方法,通过遍历虚拟点确定sink最优路径.
在上述研究基础上,笔者设计并实现了一种面向能耗均衡的传感网单移动sink数据收集方法(DGBEC,data gathering method based on one mobile sink for balanced energy consumption in sensor networks). 构建了等长间隔的sink移动轨迹,实现了基于遍历时间预判的数据收集节点休眠调度机制,均衡了全网数据收集的能耗开销.
2 网络模型笔者采用sink节点在全网移动,而各数据收集节点定期向sink上传的数据收集模式. 同文献[7]类似,笔者在网络中定义若干均匀分布的遍历位置点(以下简称“遍历点”),在一轮数据收集过程中,sink节点依次移动至每一个遍历点,进行数据收集,并需满足如下约束条件:
1) sink在各数据收集点处,仅能监听到以其通信半径
2) sink完成一轮全网数据收集的过程中,需确保网络中任意位置处的节点都有机会经过单跳,直接上传数据至sink;
3)sink每轮仅允许经过任意遍历点一次.
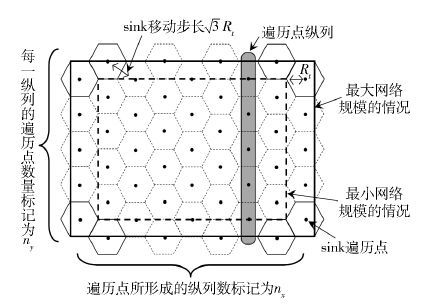
根据以上约束,首先以均匀分布的方式确定矩形网络中的各遍历点,如图 1所示. 图 1中的黑色点即为sink节点在数据收集过程中的遍历点.
根据上述约束1)和约束2),将图 1中每个正六边形的边长设为Rt,于是易知,sink的移动步长设定为$\sqrt 3 $Rt. 为方便讨论,这里将网络中遍历点的总数定义为k,且将遍历点形成的纵列数量标记为nx,由图 1可知,nx可由式(1)求出;将每一纵列中的遍历点数量标记为ny. 同时,定义临时变量qy如式(2)所示. qy为后续计算k值的重要参数.
${n_x} = \left\lceil {\left( {{M \over {0.5{R_t}}} + 1} \right)/3} \right\rceil $
(1)
${q_y} = \left\lceil {{{2N} \over {\sqrt 3 {R_t}}}} \right\rceil $
(2)
笔者要求网络中所有位置都能被遍历点所在的正六边形覆盖,因此由图 1可知,对于遍历点数都为k的网络而言,其网络规模M、N可能不同,如图 1中的实线边界框和虚线边界框所示. 由以上分析并根据网络规模参数M、N和节点通信半径Rt之间的不同关系,网络中的遍历点总数目k的取值将存在以下3种情况:
1) 情况1 当qy为奇数时,根据上述分析可知,无论nx为奇数或偶数,都有
ny=(qy+1)/2
(3)
${1 \over 2}\left\lceil {\left( {{M \over {0.5{R_t}}} + 1} \right)/3} \right\rceil \left( {\left\lceil {{{2N} \over {\sqrt 3 {R_t}}}} \right\rceil + 1} \right)$
(4)
2) 情况2 当qy为偶数,且nx也为偶数时,根据上述定义可知,纵向上的遍历点数ny的取值为
${n_y} = \left\{ \matrix{
{q_y}/2, \hfill \cr
{q_y}/2 + 1, \hfill \cr} \right.$
(5)
$\eqalign{
& k = {{{n_x}} \over 2}{{{q_y}} \over 2} + {{{n_x}} \over 2}\left( {{{{q_y}} \over 2} + 1} \right) = {n_x}\left( {{{{q_y} + 1} \over 2}} \right) = \cr
& {1 \over 2}\left\lceil {\left( {{M \over {0.5{R_t}}} + 1} \right)/3} \right\rceil \left( {\left\lceil {{{2N} \over {\sqrt 3 {R_t}}}} \right\rceil + 1} \right) \cr} $
(6)
3) 情况3 当qy为偶数,且nx为奇数时,根据上述定义可知,纵向上的遍历点数ny的取值情况仍符合式(5),但由于nx为奇数,因此遍历点的奇数列比偶数列多1,由此易知
$\eqalign{
& k = \left( {{{{n_x} + 1} \over 2}} \right){{{q_y}} \over 2} + \left( {{{{n_x} - 1} \over 2}} \right)\left( {{{{q_y}} \over 2} + 1} \right) = \cr
& {n_x}\left( {{{{q_y} + 1} \over 2}} \right) - {1 \over 2} = \cr
& {1 \over 2}\left\lceil {\left( {{M \over {0.5{R_t}}} + 1} \right)/3} \right\rceil \left( {\left\lceil {{{2N} \over {\sqrt 3 {R_t}}}} \right\rceil + 1} \right) - {1 \over 2} \cr} $
(7)
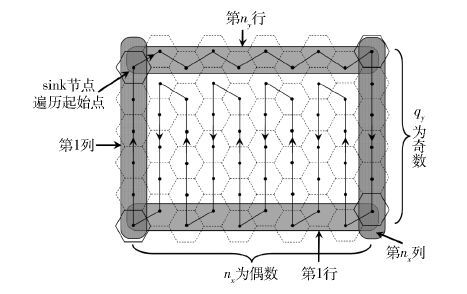
在数据收集阶段,sink从网络左上角的第1个遍历点开始顺时针匀速移动,速度为v. 令sink在每个遍历点的停留时间均为t1,并令sink节点完成一轮对全网数据收集的时间为T. 为分析方便,这里以矩形无线传感网的左下角为坐标轴原点,将网络中的遍历点划分为ny行和nx列,并将横向轴上相邻的2层遍历点视为1行,将纵向轴上的1列遍历点视为1列,如图 2所示. 假设任意一个正六边形的中心点为全网的第ly行和第lx列的遍历点,并假设网络中的各个随机部署的数据收集节点已确定了自身归属的正六边形,即已获知其所在区域正六边形的lx和ly值. 定义在一轮全网数据收集的过程中,任意一个遍历点被sink节点访问到的次序为Q,显然Q∈[1,k]. 此时,sink的遍历路径结构和网络中遍历点的行列编号如图 2所示. 根据网络几何关系和sink的移动方向,可知
1) 当ly= $\left( {{{{q_y} + 1} \over 2}} \right)$ ,即ly= ${1 \over 2}\left( {\left\lceil {{{2N} \over {\sqrt 3 {R_t}}}} \right\rceil + 1} \right)$时,Q=lx;
2) 当0<ly< $\left( {{{{q_y} + 1} \over 2}} \right)$,即0<ly< ${1 \over 2}\left( {\left\lceil {{{2N} \over {\sqrt 3 {R_t}}}} \right\rceil + 1} \right)$时,
$Q = \left\{ \matrix{
{n_x} + \left( {{n_x} - {l_x}} \right)\left( {{{{q_y} + 1} \over 2} - 1} \right) + {l_y},{l_x}{\rm{为奇数}} \hfill \cr
{n_x} + \left( {{n_x} - {l_x}} \right)\left( {{{{q_y} + 1} \over 2} - 1} \right) + \left( {{{{q_y} + 1} \over 2} - {l_y}} \right),{l_x}{\rm{为偶数}} \hfill \cr} \right.$
(8)
$Q = \left\{ \matrix{
{n_x} + {1 \over 2}\left( {{n_x} - {l_x}} \right)\left( {\left\lceil {{{2N} \over {\sqrt 3 {R_t}}}} \right\rceil - 1} \right) + {l_y},{l_x}{\rm{为奇数}} \hfill \cr
{n_x} + {1 \over 2}\left( {{n_x} - {l_x}} \right)\left( {\left\lceil {{{2N} \over {\sqrt 3 {R_t}}}} \right\rceil - 1} \right) + \hfill \cr
\left[ {{1 \over 2}\left( {\left\lceil {{{2N} \over {\sqrt 3 {R_t}}}} \right\rceil + 1} \right) - {l_y}} \right],{l_x}{\rm{为偶数}} \hfill \cr} \right.$
(9)
为验证DGBEC算法的能量效率,对其单轮数据收集能耗开展实验. 同基于虚拟点优先级的移动sink数据收集方法虚拟节点策略(VNP,virtual nodes priority)[7]算法和依次遍历全网所有节点的基于效用的贪婪启发式交会点找寻(RP- UG,rendezvous points finding with a utility-based greedy heuristic)[1]算法进行比较,仿真参数的设置如表1所示.
| 表1 单轮数据收集能耗的仿真参数设置 |
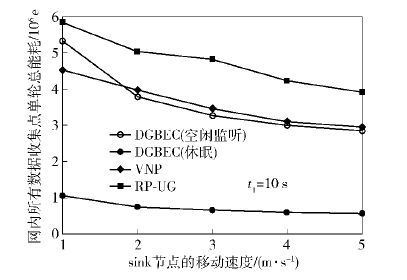
将sink在各遍历点停留的时间设为10 s时的能耗仿真结果如图 3所示. 易知,随着sink移动速度的不断增大,各种算法下的单轮数据收集能耗均有所降低,且对于空闲监听模式下的DGBEC算法、VNP算法和RP- UG算法而言,其能耗的下降幅度较大. 这是因为随着sink移动速度的提升,数据收集点的上传时间间隔相应减小,使得其数据收集量、单轮空闲监听能耗和通信能耗均有所降低.
此外,从总体上看,DGBEC算法在各模式下的能耗情况均优于VNP和RP- UG算法. VNP算法尽管利用了虚拟点寻找最佳sink遍历点,但数据收集点与sink之间往往存在多跳的可能,无形之中增大了通信开销;R P- UG算法虽然也能根据路径长度和能耗指标之间的关系来确定路径,但同样并未考虑数据收集点与sink的间距.
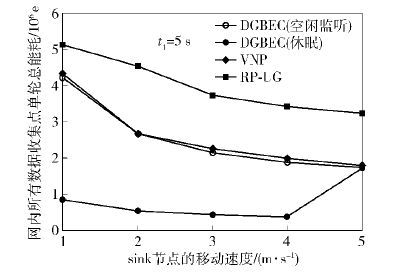
图 4为将sink在遍历点的停留时间设为5 s时的实验结果. 可以看出,相对于10 s时的情况,所有算法的单轮数据收集能耗均有所降低. 此时,不仅sink的遍历周期变短,各数据收集点的上传时间也相应减少,故数据收发的开销变小. 相对而言,VNP算法与空闲监听下的DGBEC算法的能耗差距进一步缩小,变化情况也基本一致.
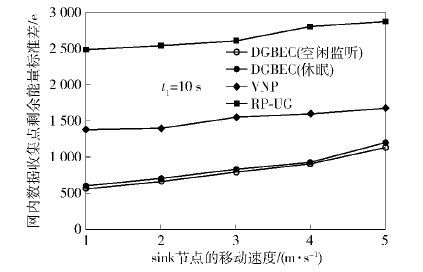
图 5验证了DGBEC算法的能耗均衡性. 令节点初始能量为106e,以网内超过50%节点的剩余能量小于103e为实验终止条件. 易知,相对于VNP和RP- UG算法,DGBEC算法的能耗均衡性较好. 这是因为DGBEC算法设置了基于固定等步长的遍历点,可确保网内任意数据收集点与遍历点的单跳距离不大于
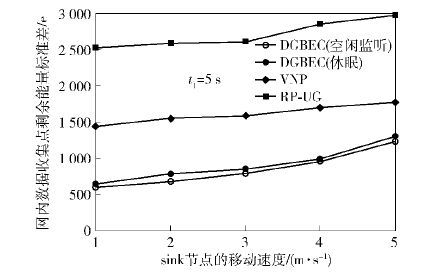
将sink在各遍历点的停留时间设为5 s后的能耗均衡性情况如图 6所示. 易知,各算法下的剩余能量标准差相对于t1=10 s时,均略有增大. 这同样是由于在生命期内,各算法下的数据上传次数变多而造成的. 但由于数据收集点的工作模式近似相同,因此DGBEC算法的整体均衡性更好.
5 结束语笔者面向不同网络规模,设计了一种基于等步长固定遍历点的移动sink数据收集方法. 实验结果表明,该方法在数据收集区域覆盖度和能耗均衡性等方面,均表现良好. 下一步将针对该移动模型下的数据收集实时性问题开展进一步的研究与讨论.
| [1] | Xing Guoliang, Wang Tian, Xie Zhihui, et al. Rendezvous planning in wireless sensor networks with mobile elements[J]. IEEE Transactions on Mobile Computing, 2008, 7(12):1430-1443.[引用本文:2] |
| [2] | Konstantopoulos C, Pantziou G, Gavalas D, et al. Data mules:modeling a three-tier architecture for sparse sensor networks[C]//Proc 1st IEEE Int' l Workshop on Sensor Network Protocols an Applications, 2003:30-41.[引用本文:2] |
| [3] | Anastasi G, Conti M, Gregori E, et al. Motes sensor networks in dynamic scenarios:an experimental study for pervasive applications in urban environments[J]. International Journal of Ubiquitous Computing and Intelligence, 2007, 1(1):9-16.[引用本文:2] |
| [4] | Chakrabarti A, Sabharwal A, Aazhang B. Communi cation power optimization in a sensor network with a path-constrained mobile observer[J]. ACM Trans actions on Sensor Networks, 2006, 2(3):297-324.[引用本文:3] |
| [5] | Liang Song, Hatzinakos D. Architecture of wireless sensor networks with mobile sinks:sparsely deployed sensor[J]. IEEE Transactions on Vehicular Technology, 2007, 56(4):1826-1836.[引用本文:1] |
| [6] | Somasundara A, Ramamoorthy A, Srivastava M. Mobile element scheduling for efficient data collection in wireless sensor networks with dynamic deadlines[C]//RTSS, 2004:296-305.[引用本文:1] |
| [7] | Gao Shuai, Zhang Hongke. Optimal path selection for mobile sink in delay-guaranteed sensor networks[J]. Acta Electronic Sinica, 2011, 39(4):1-6.[引用本文:3] |