2. 南京工业大学电气工程与控制科学学院, 南京 211800
针对手眼标定过程要求机器人运动次数过多的缺点,提出了一种改进的单特征点手眼自标定方法.引入手眼关系矩阵的解耦运算,分别标定手眼旋转矩阵和平移向量.运算过程无需计算特征点位置,操作过程仅需机器人末端有5次以上平移运动和2次以上旋转运动.实验与误差分析结果表明,所提方法满足工业机器人手眼视觉测量的需求.
2. College of Electrical Engineering and Control Science, Nanjing University of Technology, Nanjing 211800, China
For the shortcoming that the excessive number of robot movement is required during the hand-eye calibration, an improved self-calibration method to hand-eye relation of robot based on a single feature point was proposed. The decoupling operation for hand-eye relation matrix was introduced, and also the hand-eye rotation matrix and translation vector were calibrated respectively. In the calibration process, the feature point position is not necessary to be calculated, but and the manipulator end effector is needed also to perform more than five times translational motions and two times rotation motions. Calibration experiment and error analysis verify that the method can meet the demand for industrial robot hand-eye vision measurement.
在机器视觉应用于机器人技术时,经常将摄像机固定在机器人手臂的末端执行器上构成手眼系统. 确定摄像机坐标系与机器人末端坐标系之间相对位置关系的过程称为机器人手眼标定[1]. 目前,不需要标定参照物的手眼自标定方法获得了学者们的普遍重视和研究[2, 3, 4, 5].
为满足工业现场的需求,笔者提出了一种改进的单特征点机器人手眼自标定方法,该方法通过引入手眼关系矩阵的解耦运算,解决原有方法要求运动次数过多的问题,并给出了实验结果和分析.
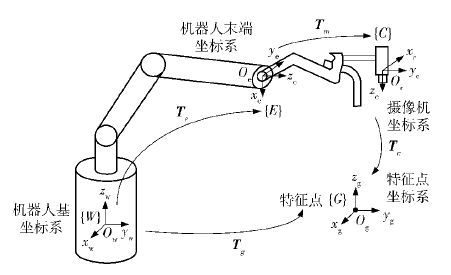
1 机器人手眼关系的标定机器人手眼关系坐标系如图 1所示.
取摄像机视场内任意可测一点为特征点,在特征点处建立坐标系G,其坐标轴与机器人基坐标系W的坐标轴平行. 在机器人末端建立坐标系E,在摄像机的光轴中心建立坐标系C. E相对于W的变换用Te表示,C相对于E的变换用Tm表示,G相对于C的变换用Tc表示,G相对于W的变换用Tg表示. 其中Tm即为机器人手眼关系矩阵,其旋转矩阵和平移向量分别记为Rm和Pm.
1.1 相对于单特征点的摄像机内外参数标定保持姿态不变,操作机器人末端带动摄像机相对于特征点沿基坐标系W 3个方向做正交平移运动. 设机器人在初始位置时的特征点为特征原点,根据相对运动原理,特征点相对于特征原点位置运动可形成多个虚拟特征点. 控制平移距离,使所得到的虚拟特征点均匀分布在以特征原点为中心的立方体的顶点或面心上,则相当于将一个立体靶标放置于摄像机之前进行标定,可利用Faugeras标定方法[6]获得摄像机的投影矩阵M,分解后得出内参数K和相对于特征原点坐标系G的外参数Tc,根据M的可解性,平移运动的次数最少为5次.
1.2 手眼旋转矩阵Rm的标定
将初始采集特征原点图像时的机器人末端位姿Te记为Te0,摄像机相对于特征原点的外参数Tc记为Tc0,由图 1的坐标系变换关系可得
TgTc0-1=Te0Tm
(1)
将式(1)各齐次矩阵表示为姿态矩阵R和位置向量P的分解形式,并用下角标标示各矩阵的对应关系,则可得
Rc0-1=Re0Rm
(2)
-Rc0-1Pc0+Pg=Re0Pm+Pe0
(3)
Rm=Re0-1Rc0-1=(Rc0Re0)-1
(4)
由于Te0可由机器人示教器读出,Tc0已由1.1节方法标定得出,因此Rc0、Re0可由Tc0和Te0提取得到,并由式(4)可求出Rm.
1.3 手眼平移向量Pm的标定重新设定机器人的末端姿态,使之与初始姿态有较大变化. 采集图像并记录机器人的末端位姿,至少采集2次图像,第i次改变姿态后,采集特征原点图像时的机器人末端位姿和摄像机外参数矩阵分别表示为Tei和Tci,其对应的旋转矩阵和平移向量分别记为Rei、Pei和Rci、Pci.
由式(2)和式(3)的对应形式可得
-ReiRmPci+Pg=ReiPm+Pei
(5)
根据摄像机的内参数模型[7]可得
Pci=zciPci1
(6)
将式(6)带入式(5)得
-zciReiRmPci1+Pg=ReiPm+Pei
(7)
将式(7)和式(3)联立,消去
Pg后得
zciReiRmPci1+(Rei-Re0)Pm=
Pe0-Pei+Rc0-1Pc0
(8)
采集n次图像构建多个形如式(8)的表达式,联立成矩阵形式为
$\eqalign{
& \left[ {\matrix{
{{R_{e1}}{R_m}{P_{c11}}} \hfill & 0 \hfill & \cdots \hfill & 0 \hfill & {{R_{e1}} - {R_{e0}}} \hfill \cr
0 \hfill & {{R_{e2}}{R_m}{P_{c21}}} \hfill & \cdots \hfill & 0 \hfill & {{R_{e2}} - {R_{e0}}} \hfill \cr
0 \hfill & 0 \hfill & \ddots \hfill & \vdots \hfill & \vdots \hfill \cr
0 \hfill & 0 \hfill & \cdots \hfill & {{R_{en}}{R_m}{P_{cn1}}} \hfill & {{R_{en}} - {R_{e0}}} \hfill \cr
} } \right]\left[ {\matrix{
{{z_{c1}}} \hfill \cr
{{z_{c2}}} \hfill \cr
\vdots \hfill \cr
{{z_{cn}}} \hfill \cr
{{P_m}} \hfill \cr
} } \right] = \cr
& \left[ {\matrix{
{{P_{e0}} - {P_{e1}} + R_{c0}^{ - 1}{P_{c1}}} \cr
{{P_{e0}} - {P_{e2}} + R_{c0}^{ - 1}{P_{c0}}} \cr
\vdots \cr
{{P_{e0}} - {P_{en}} + R_{c0}^{ - 1}{P_{c0}}} \cr
} } \right] \cr} $
(9)
式(9)中,未知量仅有zci(i=1,2,…,n)和Pm,当n≥2时,可利用最小二乘法求解,在得出Pm的同时也计算出深度值zci. 由于n最小值可取2,故Pm的标定最少需2次改变机器人末端姿态.
2 实验研究 2.1 测试实验实验采用的机器人手眼系统主要包括ABB1410工业机器人、1/3 in SONY XC - ES50CE CCD工业摄像机和DH CG410图像采集卡,图像大小为768×576像素(pixel). 设定好场景特征原点及机器人初始位置,保持末端姿态不变做正交平移运动5次,共采集5幅图像;然后相对于初始位置做2次末端旋转运动,再采集2幅图像. 每次采集图像时均记录对应的机器人末端位姿. 提取各图像特征点坐标后,应用所提改进方法得到的标定结果为 \[\eqalign{ & K = \left[ {\matrix{ {971.001} & 0 & {381.645} \cr 0 & {944.874} & {294.428} \cr 0 & 0 & 1 \cr } } \right] \cr & {R_m} = \left[ {\matrix{ { - 0.0131} & {0.9997} & { - 0.0212} \cr { - 0.9995} & { - 0.0093} & { - 0.0297} \cr { - 0.0300} & { - 0.0209} & {0.9993} \cr } } \right] \cr & {P_m} = \left[ {\matrix{ { - 208.725} & {9.041} & {410.156} \cr } } \right] \cr} \]
下面将对改进方法的实验结果进行误差分析,对影响实验结果的因素进行讨论.
2.2 误差分析1) 图像噪声对标定误差的影响
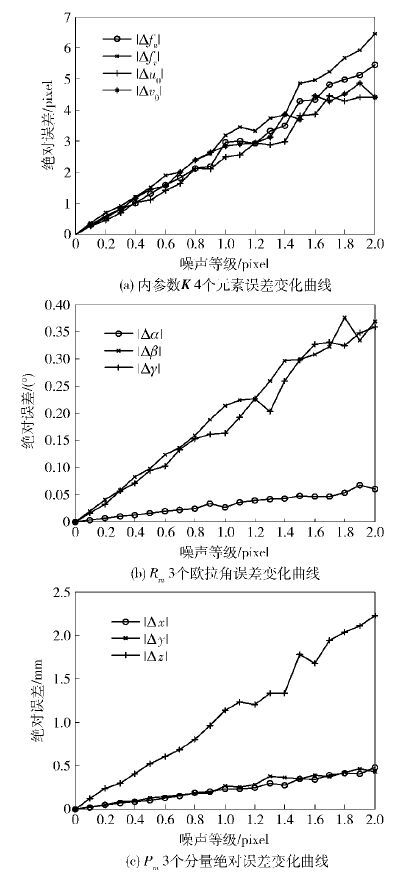
为分析图像噪声的影响,在实测图像坐标加入0~2个像素、间隔0.05像素的噪声,进行模拟实验. 在每种噪声水平下随机实验100次,取其平均值的统计结果,得到K、Rm和Pm在不同噪声水平下的误差变化曲线如图 2所示. 其中,Δfu、Δfv、Δu0和Δv0分别表示摄像机在u、v两个方向上的归一化焦距和两个方向上主点图像坐标的误差;旋转矩阵Rm用 z- y- x欧拉角α、β、γ表示,Δα、Δβ和Δγ分别表示欧拉角3个分量的误差;Δx、Δy和Δz分别表示Pm在x、y和z 3个方向分量的误差.
由图 2可见,图像噪声对K的4个元素误差影响变化趋势基本相同,1个像素等级产生2.5~3.5个像素误差;图像噪声对Rm造成的影响较小,但α和γ的误差随噪声变化增加较快;图像噪声对Pm的x、y分量影响较小,而对z分量造成的误差较大,这说明图像噪声对特征点深度值的准确估计产生较大影响,进一步影响标定的稳定性.
2) 机器人末端运动偏差对标定误差的影响
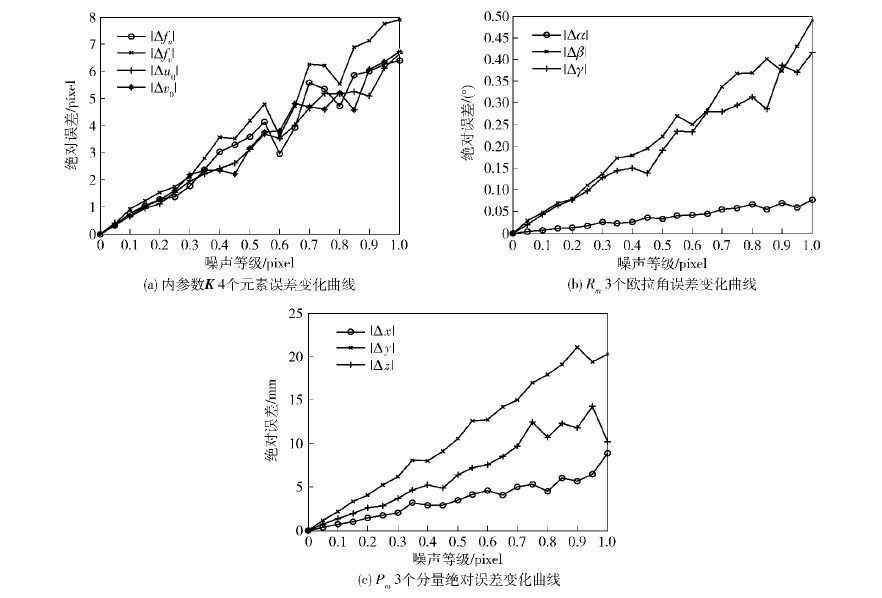
为分析机器人末端运动偏差的影响,在实际实验的平移运动分量上加入0~1 mm、间隔0.05个长度单位的偏差,而在旋转运动分量上加入0~1°、间隔0.05个角度单位的偏差,在每种偏差水平下随机实验100次,取其平均值的统计结果. 运动精度对K、Rm和Pm的误差影响变化曲线如图 3所示.
由图 3可见,机器人末端运动偏差对K的4个元素造成的误差变化趋势也基本相同,且与图像噪声造成的误差相当;运动偏差对Rm的影响比图像噪声稍大;而运动偏差对Pm的影响较大,特别是对z分量造成的误差很大,远超过图像噪声的影响.
2.3 进一步讨论与分析1)图像大小对实验结果的影响
在相同噪声和末端运动误差的情况下,将采集的图像大小变为640×480像素,与原图幅的实验结果比较,如表1所示.
由表1可见,2种不同图像大小所得到的误差实验结果相差不大,其误差主要来源于噪声的随机性. 上述结果说明,在摄像机分辨率一定的条件下,图像大小对误差像素数乃至实验结果的影响较小.
| 表1 图像大小对实验结果的影响 |
2) 特征点与摄像机间距对实验结果的影响
前述实验发现无论是图像噪声还是机器人末端运动偏差对Pm特别是其中z分量造成的误差都较大. 根据式(9),Pm与特征点的深度值是同时求解的,而z分量的方向与图像深度方向一致,由此分析深度值可能对Pm的z分量结果产生影响. 影响深度值的主要因素是特征点与摄像机的距离. 因此,选取特征点与摄像机镜面中心的3个不同间距分别进行误差实验,结果如表2所示(间距d为近似值).
由表2可见,随着特征点与摄像机间距d减小,图像噪声及运动偏差所造成的Pm误差值都同时减小,表明通过减小间距d,可以减小Pm的误差. 但随着特征点靠近摄像机,摄像机的视场范围变小,易造成摄像机运动过程中特征点移出视场的情况,多次实验表明,间距取在35~45 mm之间较为适宜.
| 表2 特征点与摄像机间距对实验结果的影响 |
3) 算法的精度与运算效率分析
为分析算法的精度与运算效率,将所提方法与文献[4]和文献[5]方法进行比较. 根据实测特征点图像坐标提取精度及ABB1410机器人的末端定位精度,取0.5像素、0.05 mm和0.05°,以及1.0像素、0.1 mm和0.1°分别作为图像和运动偏差的综合噪声水平等级1和2. 在上述2种噪声水平下各模拟实验100次,测试主机为Inter(R) Core(TM)i3- 3240、CPU 3.40 GHz,由统计平均值得到结果如表3所示.
| 表3 算法的精度与实时性分析 |
由表3可见,从算法的精度上看,所提方法与文献[5]方法基本相同,而优于文献[4]方法,说明算法具有较高的准确性. 从算法的运算效率上看,所提方法优于文献[5]方法,但不及文献[4]的方法实时性高. 究其原因,所提方法在图像降噪等过程中计算量相对较大,需在后继研究中采用更高效的降噪算法,进一步提高算法效率. 从算法精度和运算效率综合性能上看,所提方法更为适用.
根据实验结果,为保证手眼标定的精度,图像噪声的极限应控制在1像素误差范围内,机器人末端运动误差极限应控制在平移分量0.1 mm和旋转分量0.1°偏差范围内. 此时,Rm分量的误差均在0.2°以内,Pm分量最大误差不超过1.2 mm,上述平均误差结果可以满足一般工业机器人手眼视觉测量的需求.
3 结束语针对单特征点手眼标定问题,应用解耦运算思想分别标定出摄像机内参数、手眼旋转矩阵和平移向量,并通过实验进一步分析了图像噪声、机器人运动偏差、图像大小和特征点距离等因素对标定结果的影响. 与现有方法比较,改进方法操作过程简洁,算法精度较高,有利于工业现场环境下的实际应用.
| [1] | 徐德, 谭民, 李原. 机器人视觉测量与控制[M]. 北京:国防工业出版社, 2011:51-56.[引用本文:1] |
| [2] | Ma S D. A self-calibration technique for active vision system[J]. IEEE Transactions on Robotics and Automation, 1996, 12(1):114-120.[引用本文:1] |
| [3] | 杨广林, 孔令富, 王洁. 一种新的机器人手眼关系标定方法[J]. 机器人, 2006, 28(4):400-405. Yang Guanglin, Kong Lingfu, Wang Jie. A new calibration approach to hand-eye relation of manipulator[J]. Robot, 2006, 28(4):400-405.[引用本文:1] |
| [4] | 许海霞, 王耀南, 万琴, 等. 一种机器人手眼关系自标定方法[J]. 机器人, 2008, 30(4):373-378. Xu Haixia, Wang Yaonan, Wan Qin, et al. A self-calibration approach to hand-eye relation of robot[J]. Robot, 2008, 30(4):373-378.[引用本文:4] |
| [5] | 徐德, 赵晓光, 涂志国, 等. 基于单特征点的手眼系统摄像机标定[J]. 高技术通讯, 2005, 15(1):32-36. Xu De, Zhao Xiaoguang, Tu Zhiguo, et al. A simple camera calibration method for robot's hand-eye system[J]. Chinese High Technology Letters, 2005, 15(1):32-36.[引用本文:5] |
| [6] | Faugeras O D, Luong Q T, Maybank S. Camera self-calibration:theory and experiments[C]//Proc. of the Second European Conf. on Computer Vision. Berlin:Springer Verlag, 1992:321-334.[引用本文:1] |
| [7] | 张广军. 机器视觉[M]. 北京:科学出版社, 2005:69-70.[引用本文:1] |