在依赖分发者选取多项式系数、构造多项式并将多项式的函数值作为秘密份额的秘密共享方案中,半诚实的分发者可通过修改多项式系数泄漏关于秘密的信息,破坏秘密共享方案的安全性.为了解决半诚实分发者造成的秘密泄漏问题,提出了一种抗泄漏的可验证多秘密共享方案.该方案采用所有参与者共同构造多项式系数的方式,成功解决了半诚实分发者可能泄漏秘密信息的问题.与其他方案相比,新方案实现了抗半诚实分发者泄漏.同时,实验结果也表明,新方案在计算方面具有较好的性能.
In the existing multi-secret sharing schemes mainly depending ondealer selections, the polynomial coefficients constructs the polynomial and takes the value ofpolynomial function as shadows of secrets, however, the semi-honest dealer may leak information of secrets by changing the polynomial coefficients. In order to solve the problem by semi-honest dealer, the article presented a new leakage-resilient verifiable multi-secret sharing scheme The problem of leakage secret information hiddens in that the polynomial coefficients are selected and constructed by all of participants. Comparison with existing schemes which also achieve verifiable multi-secret sharing, the scheme can still work well even when the dealer leaks some secret information.It has better efficiency in terms of computation overhead.
秘密共享技术是现代密码学和信息安全的重要研究内容[1]. Shamir[2]和Blakely[3]提出的(t,n)门限秘密共享方案不适用于多秘密共享. Chang等[4]和Eslami等[5]分别基于RSA假设、离散对数假设(DLP,discrete logarithm problem)提出了可验证的多秘密共享方案. 这些方案能防止欺骗行为的发生但不能抗信息泄漏. Olimid[6]提出了一种抗分发者泄漏的秘密共享方案,但不适用于多秘密共享.
笔者在Jun[7]的基础上提出了一种高效的抗泄漏的可验证多秘密共享方案. 该方案通过采用一种同步通信模式使参与者能参与到分发者构造多项式系数的过程中,从而避免了半诚实分发者通过构造多项式系数的方式泄漏秘密的可能.
1 预备知识 1.1 密码安全的哈希函数定义1 (密码安全的哈希函数) 如果一个哈希函数H满足下述性质,那么该哈希函数被认为是密码安全的.
1) 单向性:对于$\forall $y∈H的值域,计算满足y=H(x)的x是困难的.
2) 抗碰撞性:对于$\forall $x∈H的定义域,计算满足H(x)=H(x′)的x′是困难的.
1.2 拉格朗日插值定理设$\sum\limits_{i = 1}^{k - 1} {{L_i}\left( x \right)} = \sum\limits_{i = 0}^{k - 1} {{a_i}{x^i}} $为一个k-1次多项式,其中k-1≥0,且通过k个点(x0,y0),…,(xk-1,yk-1),对于$\forall $i,有 \[{L_i}\left( x \right) = {y_i}\prod\limits_{j = 0,j \ne i}^{k - 1} {{{x - {x_j}} \over {{x_i} - {x_j}}}} = \left\{ \matrix{ {y_i},{\rm{若}}x = {x_i} \hfill \cr 0,{\rm{若}}x \ne {x_i} \hfill \cr} \right.\]
1.3 可验证(k,t,n)多秘密共享方案可验证的多密码共享方案要求满足正确性、安全性和可验证性.
定义2 (正确性) 如果分发者D是诚实的,那么由任意不小于t个参与者提供的秘密份额能正确重构秘密S.
定义3 (安全性) 如果分发者D是诚实的,那么通过任意小于t个参与者提供的秘密份额将无法得到任何关于秘密S的信息.
定义4 (可验证性) 如果分发者D是诚实的,那么参与者可验证分发者分发的秘密份额的有效性,分发者D也可验证参与重构的参与者提供的秘密份额的有效性.
可验证的秘密共享方案能防止参与者和分发者的欺骗行为,其安全性完全依靠拥有诚实的分发者. 但抗泄漏的可验证多秘密共享方案允许分发者是半诚实的.
定义5 (抗泄漏的可验证多秘密共享方案) 抗泄漏的可验证多秘密共享方案是指一个满足抗泄漏性的可验证(k,t,n)多秘密共享方案. 所谓抗泄漏性是指如果分发者D是半诚实的,敌手仍然无法获得关于秘密的任何信息.
半诚实分发者是指能通过调整构造多项式时的随机数,将泄漏给敌手的秘密信息隐藏在有效的秘密份额中而不被参与者(除敌手之外)发现的分发者. 半诚实分发者具有破坏性和隐蔽性的特点. 半诚实分发者的存在打破了只有授权的参与者才能重构秘密的约束,威胁了秘密的安全.
2 抗泄漏的可验证多密码共享方案 2.1 方案框架笔者提出的方案包括3个阶段:系统参数生成、秘密分发和秘密重构. 在秘密分发阶段,笔者采用一种同步通信模型完成秘密份额的生成与分发.
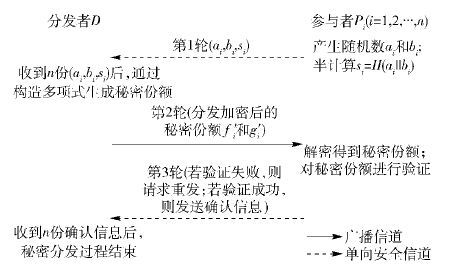
定义6 (同步通信模型) 方案的秘密分发过程包括3轮分发者与参与者之间的信息交互过程,如图 1所示.
2.2 符号定义p和q分别为2个大素数;H为一个密码安全的Hash函数;t为门限值(即重构秘密所需要的最少秘密份额数);P={P1,P2,…,Pn}为n个参与者构成的集合;S={S0,S1,…,Sk-1}为k个被共享秘密构成的集合;D为半诚实分发者.
2.3 系统参数生成p,q,S,P,t,H遵循2.2节的定义,且满足2799<p<2800,2159<q<2160,q|(p-1),产生k个秘密Si∈Zp*(i=0,1,2,…,k-1),2t+1≤n,k-1+t≤n,选择安全哈希函数H:{0,1}*→Zp*,并公布该哈希函数.
2.4 秘密分发利用同步通信模型将k个秘密分发给n个参与者P1,P2,…,Pn.
1) 第1轮通信
每个参与者Pi(i=1,2,…,n)选择2个随机数ai,bi∈Zp*,计算si=H(ai‖bi),通过安全信道将(ai,bi,si)发送给分发者D,D将si广播出去. 广播的目的是让Pi确信其发送的(ai,bi)已被D正确接收.
2) 第2轮通信(分发者分发秘密份额)
分发者D在本地记录接收到的(ai,bi,si). 当收齐所有参与者发来的(ai,bi,si)之后,D根据秘密个数k与门限t的关系,分以下2种情况构造多项式.
① 当t≥k时,分发者D构造t-1阶多项式. \[\eqalign{ & a{'_{i'}} = \left\{ \matrix{ {S_{i'}},0 \le i' < k \hfill \cr \sum\limits_{j' = 0}^t {{a_{i' + j'}},k \le i' \le t - 1} \hfill \cr} \right. \cr & b{'_{i'}} = \left\{ \matrix{ {b_1} + {b_2} + \cdots + {b_t},i' = 0 \hfill \cr \sum\limits_{j' = 0}^t {{b_{i' + j'}},i' = 1,2, \cdots t - 1} \hfill \cr} \right. \cr} \]
根据得到的(a′ i′,b′ i′)(i′=0,1,2,…,t-1)构造多项式为
$f\left( x \right) = \sum\limits_{i' = 0}^{t - 1} {a{'_{i'}}{x^{i'}}\bmod p} $
(1)
$g\left( x \right) = \sum\limits_{i' = 0}^{t - 1} {b{'_{i'}}{x^{i'}}\bmod p} $
(2)
计算vi=H(f(i)‖g(i)),f′ i=ai+f(i),g′ i=bi+ g(i),其中f(i)和g(i)分别为多项式(1)和 式(2)中x=i(i=1,2,…,n)的函数值;并计算cj=b′ j+ra′ jmod p(j=0,1,…,t-1),其中r=H(v1‖v2‖…‖vn). 分发者D广播(f′ i,g′ i,vi)(i=1,2,…,n)和cj(j=0,1,…,t-1).
② 当t<k时,分发者D构造k-1阶多项式. \[\eqalign{ & a{'_{i'}} = {S_{i'}},i' = 0,1, \cdots ,k - 1 \cr & b{'_{i'}} = \cr & \left\{ \matrix{ \left( {{a_1} + {b_1}} \right) + \left( {{a_2} + {b_2}} \right) + \cdots + \left( {{a_t} + {b_t}} \right),i' = 0 \hfill \cr \sum\limits_{j' = 0}^t {\left( {{a_{i' + j'}} + {b_{i' + j'}}} \right),i' = 1,2, \cdots k - 1} \hfill \cr} \right. \cr} \]
根据得到的(a′ i′,b′ i′)(i′=0,1,2,…,k-1)构造多项式为
$f\left( x \right) = \sum\limits_{i' = 0}^{k - 1} {a{'_i}{x^i}\bmod p} $
(3)
$g\left( x \right) = \sum\limits_{i' = 0}^{k - 1} {b{'_i}{x^i}\bmod p} $
(4)
计算vi=H(f(k-t+i)‖g(k-t+i)),f′ k-t+i=ai+f(k-t+i),g′ k-t+i=bi+g(k-t+i),其中f(k-t+i)和g(k-t+i)分别为多项式(3)和式(4)中x=k-t+i(i=1,2,…,n)的函数值;并计算当x′=1,2,…,k-t时f(x′)和g(x′)的函数值. 同时计算cj=b′ j+ra′ jmod p(j=0,1,…,k-1),其中r=H(v1‖v2‖…‖vn). D广播(f′ k-t+i,g′ k-t+i,vi)(i=1,2,…,n),cj(j=0,1,…,t-1)和(f(x′),g(x′))(x′=1,2,…,k-t).
3) 第3轮通信(参与者验证各自的秘密份额)
① 当t≥k时,Pi(i=1,2,…,n)通过(ai,bi)和(f′ i,g′ i),计算得到f(i)和g(i)并验证
${v_i}\mathop = \limits^? H\left( {f\left( i \right)||g\left( i \right)} \right)$
(5)
$g\left( i \right) + rf\left( i \right)\mathop = \limits^? \sum\limits_{j = 0}^{t - 1} {{c_j}{i^j}\bmod p} $
(6)
② 当t<k时,Pi(i=1,2,…,n)通过(ai,bi)和(f′ k-t+i,g′ k-t+i),计算得到f(k-t+i)和g(k-t+i)并验证
${v_i}\mathop = \limits^? H\left( {f\left( {k - t + i} \right)||g\left( {k - t + i} \right)} \right)$
(7)
$g\left( {k - t + i} \right) + rf\left( {k - t + i} \right)\mathop = \limits^? \sum\limits_{j = 0}^{t - 1} {{c_j}{i^j}\bmod p} $
(8)
分发者先验证参与者提供的秘密份额的有效性,验证通过后再重构秘密. 假设参与者Pi(i=1,2,…,t)与D共同重构秘密S0,S1,…,Sk-1. 当t≥k时,Pi分别将f(i)和g(i)通过安全信道发送给分发者D;当t<k时,Pi分别将f(k-t+i)和g(k-t+i)通过安全信道发送给D.
2.5.1 验证D对Pi提供的秘密份额进行验证. 当t≥k时,验证式(5)和式(6)是否成立;当t<k时,验证式(7)和式(8)是否成立. 若验证成功,则D接收Pi发送的秘密份额,否则拒绝接收并要求Pi重发.
2.5.2 重构D对P1,P2,…,Pt发送的秘密份额在验证通过后,根据接收到的t个秘密份额,利用拉格朗日插值法恢复多项式.
1) 当t≥k时,根据收到的t个秘密份额可恢复t-1次多项式为
$f\left( x \right) = \sum\limits_{i = 1}^t {f\left( i \right)} \prod\limits_{j = 1,j \ne i}^t {{{x - j} \over {i - j}}} = \sum\limits_{i = 0}^{t - 1} {a{'_{i'}}{x^i}} $
(9)
2) 当t<k时,根据收到的t个秘密份额和广播 得到的k-t个秘密份额(f(x′),g(x′))(x′=1,2,…,k-t)恢复k-1次多项式为
$f\left( x \right) = \sum\limits_{i = 1}^k {f\left( i \right)} \prod\limits_{j = 1,j \ne i}^k {{{x - j} \over {i - j}}} = \sum\limits_{i = 0}^{k - 1} {a{'_{i'}}{x^i}} $
(10)
根据2.4节多项式的构造过程可知,多项式的前k个系数即为k个共享秘密. 也就是说,Si′=a′ i′(i′=0,1,…,k-1),分发者D成功重构秘密.
3 方案分析下面仅就t≥k的情况对方案进行正确性、安全性、可验证性和抗泄漏性方面的分析;在t<k情况下的分析过程类似,在此省略.
3.1 正确性分析定理1 该方案可实现根据任意大于等于t个有效秘密份额,分发者D能成功重构k个秘密.
证明 假设D接收到Pi发送的有效秘密份额((f(i),g(i))(i=1,2,…,t). 根据拉格朗日插值特性,D可唯一确定1个t-1阶多项式f(x). f(x)的前k个参数就是被共享的k个秘密,因此D重构成功.
3.2 安全性分析密码哈希函数具有易于构造且运算速度快的特点,这些特点使密码哈希函数较适用于实际应用,因此该方案选择密码哈希函数作为安全基础.
定理2 该方案可实现根据任意小于t个有效秘密份额,敌手将无法获取关于秘密的任何信息.
证明 假设敌手通过贿赂等方式获得t-1个参与者Pi(i=1,2,…,t-1)的秘密份额((f(i),g(i)). 因为哈希函数的单向性使敌手无法根据D广播的vi=H(f(i)‖g(i))(i=1,2,…,n)获得除上述t-1个秘密份额以外的任何信息. 敌手根据已获得t-1个秘密份额和g(i)的计算式(2)可得
$f\left( i \right) = \sum\limits_{j = 0}^{t - 1} {a{'_j}{i^i},i = 1,2, \cdots t - 1} $
(11)
cj=b′ j+ra′ j,j=0,1,…,t-1
(12)
敌手的目标是求出式(12)中的2t个变量(a′ 0,a′ 1,…,a′ t-1; b′ 0,b′ 1,…,b′ t-1),但式(11)和式(12)共有2t-1个等式,因此敌手无法获得任何关于a′ 0,a′ 1,…,a′ t-1的正确信息. 该方案满足安全性要求.
3.3 可验证性分析定理3 实施该方案,如果分发者D是诚实的,那么参与者可验证D分发的秘密份额的有效性,同时D也可验证参与者是否存在欺骗行为.
证明 下面分别从参与者角度和分发者角度证明该方案的可验证性. 先从参与者角度进行证明. 参与者Pi接收到1个伪造秘密份额(f(i)*,g(i)*),其中伪造秘密份额满足
vi*=H(f(i)*‖g(i)*)≠vi=H(f(i)‖g(i))
(13)
g(i)*+H(v1‖…‖vi*‖…‖vn)f(i)*≠$\sum\limits_{j = 0}^{t - 1} {{c_j}{i^i}} $
(14)
根据方案可知,式(13)和式(14)成立,Pi要求D重新发送,故Pi能验证收到的秘密份额是否有效. 再采用反证法从分发者角度进行证明. 假设D不具有可验证性,即参与者Pi发送伪造子秘密
(f(i)*,g(i)*),D成功接收,则有
vi*=H(f(i)*‖g(i)*)=H(f(i)‖g(i))=vi
(15)
因为式(15)与安全哈希函数的抗碰撞性相矛盾,所以假设不成立,D能验证参与者提供的秘密份额是否有效. 综上所述可知,该方案具有可验证性.
3.4 抗泄漏性分析定理4 分发者D为泄漏分发者,方案仍然是安全的,即敌手无法获得任何关于秘密的信息.
证明 首先,D严格执行该方案,负责秘密分配和重构,秘密分配过程采用广播的方式,从而避免了D单独向敌手泄漏消息的可能. 其次,因为安全哈 希函数的单向性,D不可能通过公布的vi=H(f(i)‖ g(i))(i=1,2,…,n)向敌手泄漏关于秘密的任何信息. 再次,D不可能通过公布的cj=b′ j+ra′ jmod p(j=0,1,…,t-1)向敌手泄漏关于秘密的任何信息. 这是因为任意t-1个参与者无法确定a′ j和b′ j的值,从而无法获得任何关于多项式的信息. 最后,分发者不可能通过公布的(f′ i,g′ i)(i=1,2,…,n)向敌手泄漏关于秘密的任何信息. 这是因为f′ i=ai+f(i),g′ i=bi+g(i),其中ai是由Pi随机选择的,f(i)是当x=i时多项式f(x)(见式(1))的函数值,而多项式f(x)是由系数a′ i决定的. 因此,f′ i是确定的,D不能泄漏关于秘密的任何消息. 通过同样的分析过程可知,D也不可能通过g′ i泄漏关于秘密的任何消息.
4 方案比较分析下面将从以下几个方面对本方案进行分析,即是否能实现多秘密共享、计算代价、安全假设,是否具有抗泄漏性. 多秘密共享是指能1次实现多个秘密的分享(也可用于实现共享1个超长的单秘密,先将单秘密分成多个部分,然后实施多秘密共享方案);计算代价是指诸如大循环群里的模幂运算、长比特运算等耗时运算带来的计算开销;安全假设是指敌手攻破方案等同于解决了困难假设;抗泄漏性是指方案中存在半诚实分发者时,方案是否安全. 本方案与其他方案的比较如表1所示.
| 表1 本方案与已有的秘密共享方案的比较 |
本方案和Jun[7]方案的安全假设是基于密码哈希函数,所以方案主要计算耗时为长比特的哈希计算,而CHY[4]、EA[5]和Olimid[6]等方案的安全假设是基于RSA或DLP等困难问题,因此方案的主要计算耗时为模幂运算. 对运算耗时进行实验,实验采用Thinkpad T540p笔记本式计算机(配置为Win8系统、2.4 GHz的CPU主频),利用Crypto+ +(版本为5.6.2)对SHA1和模幂
Jun[7]方案无法抵抗半诚实者泄漏攻击,本方案通过采用所有参与者共同构造多项式系数的方式,有效地解决了由分发者独立构造多项式系数而引起的泄漏问题.
5 结束语笔者提出了一种抗泄漏的可验证多秘密共享方案,能抵抗半诚实分发者有意识地向敌手泄漏秘密信息,该方案采用密码哈希函数作为安全假设,从而能以较小的计算代价实现多秘密共享. 未来研究工作主要包括提高方案的通信效率和降低方案对单向安全信道的依赖.
| [1] | 王锋, 谷利泽, 郑世慧, 等. 可验证的多策略秘密共享方案[J]. 北京邮电大学学报, 2010, 33(6):72-75. Wang Feng, Gu Lize, Zheng Shihui, et al. A verfiable multi-policy secret sharing scheme[J]. Journal of Beijing University of Posts and Telecommunications, 2010, 33(6):72-75.[引用本文:1] |
| [2] | Shamir A. How to share a secret[J]. Communications of the ACM, 1979, 22(11):612-613.[引用本文:1] |
| [3] | Blakley G R. Safeguarding cryptographic keys[C]//Proceedings of the National Computer Conference. New York, USA:AFIPS, 1979:313-317.[引用本文:1] |
| [4] | Chang Tingyi, Hwang Minshiang, Yang Weipang. An improvement on the Lin-Wu(t, n) threshold verifiable multi-secret sharing scheme[J]. Applied Mathematics and Computation, 2005, 163(1):169-178.[引用本文:3] |
| [5] | Eslami Z, Ahmadabadi J Z. A verifiable multi-secret sharing scheme based on cellular automata[J]. Information Sciences, 2010, 180(15):2889-2894.[引用本文:3] |
| [6] | Olimid R F. Dealer-leakage resilient verifiable secret sharing[EB/OL]. IACR Cryptology ePrint Archive, 2014. http://eprint.iacr.org/2014/735.[引用本文:3] |
| [7] | Jun S. Efficient verifiable multi-secret sharing scheme based on Hash function[J]. Information Sciences, 2014, 278(9):104-109.[引用本文:4] |