2. 中国科学技术大学电子工程与信息科学系, 合肥 230027;
3. 北京邮电大学民族教育学院, 北京 102209
为解决Turbo-OVCDM译码复杂度随码率指数增长的问题,提出了一种新的、通用的Turbo-OVCDM编译码方案.该方案包括1)在发送端由2个或多个Turbo-OVCDM低速率码的码字通过直接的叠加编码生成高速率码的码字;2)在接收端通过串行干扰抵消进行译码.与传统的由单个编码矩阵直接构造重叠码分复用方法相比,新方案的译码复杂度大大降低.性能仿真证实了新方案的可行性.
2. Department of Electronic Engineering and Information Science, University of Science and Technology China, Hefei 230027, China;
3. School of Ethnic Minority Education, Beijing University of Posts and Telecommunications, Beijing 102209, China
The decoding complexity of traditional type of Turbo-overlapped code division multiplexing (OVCDM) increases exponentially with the code rate. To solve this problem, a new Turbo-OVCDM coding and decoding approach was proposed. The maximum sum-rate achieving strategy in Gaussian multiple access channels was used to construct point-to-point coding scheme. Superposition of two or more Turbo-OVCDM codes and serial interference cancellation were applied for coding and decoding respectively. Numerical results demonstrate the feasibility of the proposed approach.
Turbo-OVCDM[1, 2, 3]在重叠码分复用(OVCDM，overlapped code division multiplexing)[4]的基础上引入了类似Turbo码的结构，已报道的性能结果与3GPP Turbo码[5]相当，而由于编码输出趋近高斯分布，其理论性能极限则更优. 但其译码复杂度大致随码率增加呈指数增长. 笔者提出在点对点信道上应用类似于高斯多址信道的编码策略，设计了叠加编 码- 串行干扰抵消译码方案. 由于总的译码复杂度与其中单层编码的最大复杂度处于同一量级，因此译码复杂度的问题能够得到较好的解决，且并不影响编码性能.
1 OVCDM和Turbo-OVCDM
OVCDM编码结构如图 1所示. 设输入复值符号序列为
S=[s0,s1,…,sn]，符号取自某个集合，如二进制相移键控(BPSK，binary phase shift keying)符号集(若直接对二元序列进行OVCDM编码，则将二元序列映射为BPSK符号). 最简单的OVCDM是一个码率为1的卷积扩展. 给定长为L的复值扩展序列为
C=[c0,c1,…,cL-1]
(1)
\[{{x}_{n}}=\sum\limits_{i=0}^{\min \left\{ n,L-1 \right\}}{{{c}_{i}}{{s}_{n-i}}}\]
(2)
X=S*C
(3)
$C = \left[ {\matrix{
{{C_0}} \cr
{{C_1}} \cr
\vdots \cr
{{C_{K - 1}}} \cr
} } \right] = \left[ {\matrix{
{{c_{0,0}}} & {{c_{0,1}}} & \cdots & {{c_{0,L - 1}}} \cr
{{c_{1,0}}} & {{c_{1,1}}} & \cdots & {{c_{1,L - 1}}} \cr
\vdots & \vdots & {} & \vdots \cr
{{c_{K - 1,0}}} & {{c_{K - 1,1}}} & \cdots & {{c_{K - 1,L - 1}}} \cr
} } \right]$
(4)
该矩阵称作OVCDM编码矩阵，其输入为K路并行的符号序列Sk=[sk,0,sk,1,…,sk,n]，k=0,1,…,K-1，输出为
${x_n} = \sum\limits_{k = 0}^{K - 1} {\sum\limits_{i = 0}^{\min \left\{ {n,L - 1} \right\}} {{c_{k,i}}{s_{k,n - i}}} } $
(5)
因此，OVCDM为一个并行的复数域卷积编码模型. 可采用BCJR(Bahl，Cocke，Jelinek and Raviv)算法[6]对OVCDM进行译码. 类似于对卷积码最优译码的复杂度分析可得，对于一定的输入符号集，OVCDM的译码复杂度随码率和编码约束长度的增大分别都呈指数增长. OVCDM的约束长度可设计为2～3，因此在高码率时降低译码复杂度是一个主要问题.
 | 图1 OVCDM编码器 |
Turbo-OVCDM采用了类似Turbo码的结构，在OVCDM的基础上引入了编码器的串行级联结构或乘积结构、大尺寸交织器和迭代译码算法. 典型的Turbo-OVCDM编码器结构如图 2所示. 实现的码率为2个OVCDM编码器码率的乘积. 其译码方法即一般迭代译码算法.
 | 图2 典型的Turbo-OVCDM编码器结构 |
M用户离散时间复值高斯多址信道模型为
$Y\left[ i \right] = \sum\limits_{m = 1}^M {{X_m}\left[ i \right] + Z\left[ i \right]} $
(6)
$\sum\limits_{i \in P\left( X \right)} {{R_i}} \le \log \left( {1 + \left( {\sum\limits_{i \in P\left( X \right)} {{P_i}} } \right)/{\sigma ^2}} \right)$
(7)
所有P(X)确定的2M-1个具有如上形式的不等式共同确定了高斯多址信道的容量域. 注意到，当1个用户的速率达到单用户(即假定其他用户不存在)容量时，其他用户仍可具有正的速率.
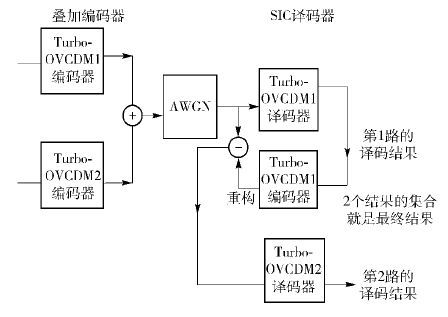
3 叠加编码构造和SIC译码笔者提出的基于叠加编码和串行干扰抵消(SIC，serial interference cancelling)译码的高码率Turbo-OVCDM系统具有如图 3所示的模型.
 | 图3 基于叠加编码和SIC译码的Turbo-OVCDM |
1) 对目标码率R，选定2种具有接近信道容量性能且输出为近似高斯分布的Turbo-OVCDM编码，分别称为码1和码2，其码率分别为R1，R2，且满足R1+R2=R.
2) 不妨设接收端需先对码1进行译码，再通过SIC对码2进行译码. 设发送功率为P(未知变量)，码1在发送端分配功率λP(0<λ<1)，码2分配功率(1-λ)P. 那么，由式(8)和式(9)消去P和σ2，解出λ，即得到2种编码的功率分配关系.
${R_1} = \log \left( {1 + {{\lambda P} \over {\left( {1 - \lambda } \right)P + {\sigma ^2}}}} \right)$
(8)
${R_2} = \log \left( {1 + {{\left( {1 - \lambda } \right)P} \over {{\sigma ^2}}}} \right)$
(9)
容易得到
λ=(2R-2R2)/(2R-1)
(10)
根据功率分配系数λ，可得码1和码2的幅度比为
$\rho = \sqrt {\lambda /\left( {1 - \lambda } \right)} = \sqrt {\left( {{2^R} - {2^{{R_2}}}} \right)\left( {{2^{{R_2}}} - 1} \right)} $
(11)
3) 使用码1和码2，分别按设定速率进行信道编码，实现R bit/符号的码率. 设码1的发送码字为n维矢量C1，码2的发送码字为n维矢量C2. 根据幅度比ρ，得到最终发送码字为
C=ρC1+C2
(12)
4) 按功率P发送码字C.
由于2路编码信号本质上是独立的，而OVCDM本身是高斯分布的，因此码字线性叠加对应于功率线性叠加.
3.2 译码过程1) 直接执行C1译码：设接收到被高斯白噪声污染的码字C′= C+w . 首先将C2视为高斯白噪声，对C′按C1的译码过程进行译码.
2) 码字重构和干扰抵消：使用第1)步的译码结果按C1的编码器进行码字重构，得到${{\hat C}_1}$. 执行SIC，得$\hat C{'_2} = C' - \rho {{\hat C}_1}$(ρ为接收端已知的编码参数).
3) 执行C2译码：对$\hat C{'_2}$，按C2的译码过程进行译码.
4) 给出结果：2个码字译码结果的集合就是最后的译码结果. 其中第2)步是SIC的关键步骤. 所谓按C1或C2的译码过程进行译码，是指执行如图 3所示的Turbo-OVCDM的迭代译码过程.
以上的编译码过程与原始的Turbo-OVCDM编码相比，不仅增加了码字叠加和SIC译码的结构，甚至还要执行2次迭代译码过程，但此时总的译码复杂度仅与码率最高的1层码的译码复杂度处于同一量级. 与传统的直接构造得到的Turbo-OVCDM编码相比，译码复杂度有了大幅度下降，即
O(ec(R1+R2))→O(ecmax {R1,R2})
(13)
这就是笔者提出的新方法最大的意义所在. 进一步地，理论上通过多次使用叠加编码方法，可使Turbo-OVCDM的译码复杂度大致随码率增长而线性增长. 这样就较好地解决了OVCDM的译码复杂度随码率增加而指数上升的问题.
4 性能仿真与分析以构造码率为8 bit/符号的OVCDM编码为例. 选用2种码率为4 bit/符号且性能较为优越的Turbo-OVCDM编码分别用于2种方案(在构造中，2种方案都用同一种码进行叠加构造，即选取的码1和码2相同，因此每种方案只需1种编码). 方案1的仿真参数(内码采用2×2编码矩阵)[1]如下： 块长度为4 796 bit，外码为非线性OVCDM(TCM)，即2/3码率16状态卷积编码器、8PSK星座映射，内码编码矩阵为$\left[ {\matrix{ {{\rm{0}}{\rm{.286 9 - 0}}{\rm{.160 6j}}} & {{\rm{ - 0}}{\rm{.110 4 + 2}}{\rm{.012 6j}}} \cr {{\rm{0}}{\rm{.112 2 + 1}}{\rm{.471 6j}}} & {{\rm{ - 0}}{\rm{.212 9 - 0}}{\rm{.012 2j}}} \cr } } \right]$ 总码率为4 bit/符号，最大迭代次数为15次，S交织器参数中的S=24. 方案2使用的仿真参数(内码采用2×1编码矩阵)[8]如下： 块长度为4 792 bit， 外码为非线性OVCDM(TCN)，即2/3码率8状态卷积编码器、8PSK映射， 内码编码矩阵为[0.462 91-0.901 70j；0.538 94+0.825 95j]， 总码率为4 bit/符号，最大迭代次数为20次， S交织器参数中的S=22.
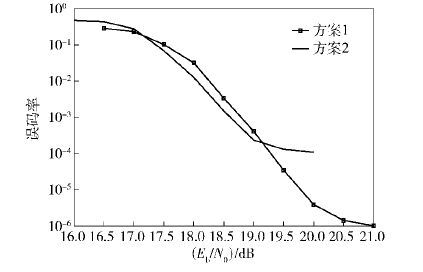
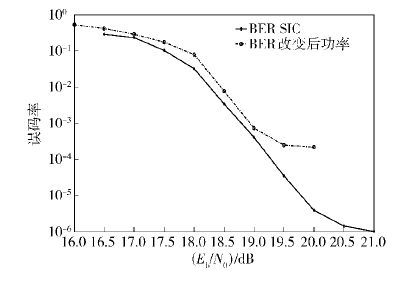
图 4给出了在分别采用方案1和方案2的2种情况下叠加编码与SIC译码性能曲线，可以看出，方案1在17～19 dB之间较差于方案2，但方案2存在较高的误码平台，在10-4量级后就很难下降，而方案1却能在21 dB下降到10-6量级. 这是因为方案2的2路编码分布相对高斯分布的近似程度较差，也就影响了叠加编码的性能. 图 4的仿真采用的是计算得到的功率比. 可见方案虽存在一定的误码平台，但仍足以实现可靠通信. 图 5略微增加了对码2的功率分配，结果总体误码率性能变差很多. 这体现了构造方法中功率比计算的正确性.
 | 图4 方案1和方案2的叠加编码与SIC译码性能 |
 | 图5 对方案1功率比进行改变后的性能 |
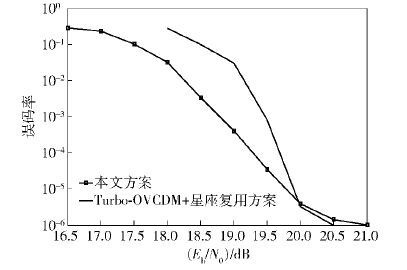
为了对比，笔者给出一种码率同样为8 bit/符号的直接构造的Turbo-OVCDM编码方案. 此方案的仿真参数如下. 由图 6可知，2种方案性能大致相当，但笔者提出的叠加编码方案的误码率下降较早，预示着进一步性能改善的潜力. 且叠加编码方案的编码块长度相对短了近1倍，所需迭代次数也少得多.
 | 图6 2种码率为8 bit/(s·Hz)方案的性能对比 |
为了对比，笔者给出一种码率同样为8 bit/符号的直接构造的Turbo-OVCDM编码方案，仿真参数如下：块长度为8 996 bit，外码为非线性OVCDM(TCM)，即2/3码率8状态卷积编码器、8QAM星座映射，内码编码矩阵为 \[\eqalign{ & C = \sqrt {1 + {{\left| {{{\sqrt 2 } \over 2}} \right|}^2} + {{\left| {{{\rm{e}}^{{\pi \over 4}j}}} \right|}^2} + {{\left| {{{\sqrt 2 } \over 2}{{\rm{e}}^{{\pi \over 4}j}}} \right|}^2}} \cdot \cr & {\left[ {\matrix{ 1 & {{{\sqrt 2 } \over 2}} & {{{\rm{e}}^{{\pi \over 4}j}}} & {{{\sqrt 2 } \over 2}{{\rm{e}}^{{\pi \over 4}j}}} \cr } } \right]^{\rm{T}}} \cr} \] 最大迭代次数为60次，S交织器参数中的S=25.
5 结束语笔者提出一种通用的高码率Turbo-OVCDM的编码构造方法. 该方法借鉴了高斯多址信道的编码方法，通过叠加编码和SIC译码，能在保持Turbo-OVCDM编码逼近信道容量极限性能的同时，使其译码复杂度不再随码率增加而指数上升. 对编码实例的仿真和与直接构造Turbo-OVCDM编码的性能对比，证实了方案的可行性. 此外，笔者给出的这种叠加编码的构造和编译码方法，也适用于任何具有近似高斯分布的编码输出的可达容量编码.
| [1] | Zhou Suhua, Fang Li, Li Daoben. A novel symbol-interleaved serially concatenated overlapped multiplexing system[C]//20092nd Conference on Power Electronics and Intelligent Transportation System(PEIT). Shenzhen:IEEE Computer Society, 2009:373-376.[引用本文:2] |
| [2] | Zhou Suhua, Fang Li, Li Daoben. Coded overlapped code division multiplexing system with Turbo product structure[J]. The Journal of China Universities of Posts and Telecommunications, 2010, 17(2):25-27.[引用本文:1] |
| [3] | Sun Peng, Li Daoben, Fang Li. Design of simplified overlapped code division multiplexing system[C]//2011 International Conference on Wireless Communications and Signal Processing(WCSP). Nanjing:IEEE, 2011:9-11.[引用本文:1] |
| [4] | Li Daoben. An overlapped code division multiplexing method, PCT/CN2007/000536[P]. 2007-02-14.[引用本文:1] |
| [5] | 3GPP TS 36. 212. Multiplexing and channel coding(Release 8), V8. 9. 0[S]. Sophia Antipolis, France:3GPP, 2009:8-20.[引用本文:1] |
| [6] | Bahl L R, Cocke J, Jelinek F, et al. Optimal decoding of linear codes for minimizing symbol error rate[J]. IEEE Trans Inform Theory, 1974, 20(2):284-287.[引用本文:1] |
| [7] | Cover T M, Thomas J A. Elements of information theory[M]. 2nd ed. Hoboken, New Jersey:Wiley, 2006.[引用本文:1] |
| [8] | Zhou Suhua, Gao Song, Li Daoben. Improved serially concatenated overlapped multiplexing system and performance[C]//Proceedings of the 2012 International Conference on Information Technology and Software Engineering. Volume 210 of Lecture Notes in Electrical Engineering. Beijing:Springer Berlin Heidelberg, 2012:183-189.[引用本文:1] |