提出一种并行组合脉冲的多带脉冲超宽带通信系统,利用r-组合数据映射算法实现发送脉冲和子带的灵活选择.构建系统模型,并对系统的比特误码性能进行仿真分析.结果表明,大信噪比条件下并行组合脉冲的多带脉冲超宽带系统的比特误码性能优于常规多带脉冲超宽带系统,并可实现不同的数据传输速率.
A multiband impulse radio ultra wideband (MIR UWB) communication system based on parallel combinatory pulses was proposed, in which the flexible selection of transmission pulses and subbands can be realized by using r-combinatory data mapping algorithm. The system model was given and the bit error rate (BER) performance was simulated and analyzed. It is shown that BER performance of the proposed system is better than that of the traditional system under the condition of large signal-to-noise ratio, and different transmission data rate can be obtained as well.
脉冲超宽带(IR UWB，impulse radio ultra wideband)采用窄脉冲信号传递信息，具有传输速率高、安全性高、功耗低等特点，在高速无线通信和低截获概率通信领域具有极大优势[1]. 为进一步提高传输速率，Paquelet等[2]提出多带脉冲超宽带(MIR UWB，multiband impulse radio ultra wideband)的思想和系统结构. 这一概念和结构的提出，可满足室内短距离无线多媒体通信网络和特殊环境下(金属舱或密闭空间)高速传感器网络物理层设计的需要. Mittelbach等[3]修正了系统模型，证明传输速率可进一步提升. Dehner等[4]研究了MIR UWB系统中的高速共存信道编码，可显著提升系统在干扰存在情况下的比特误码(BER，bit error rate)性能. 但上述系统往往占用美国联邦通信委员会(FCC，federal communications commission)规划的整个频带，并选择所有子带进行传输，频谱使用的灵活性大大降低.
笔者提出一种并行组合脉冲MIR UWB通信系统，利用数据映射算法，随机、动态地选择部分子带来传输信息，既可增加频谱划分的灵活性，又可实现不同的数据传输速率.
1 MIR UWB通信系统概述MIR UWB通信系统是在传统单带脉冲超宽带基础之上发展而来的一种并行结构的通信系统. 在发射端，MIR UWB通信系统利用滤波器组或振荡器组产生一系列子带脉冲，并使其占有规定子带[4]，然后将待传输信息串/并转换后与各子带及其时域脉冲相对应，各自调制后再合成为1路信号经天线发送出去，可采用的调制方式有开关键控、脉冲幅度调制、脉冲位置调制等. 在接收端，接收信号首先经带通滤波器组滤波后转换为各子带信号，之后在各个子带上根据信号的调制方式进行独立的解调和判决，最后经并/串转换恢复出原始的发送数据.
陈丽丽等[5]采用了长球面波函数[6](PSWF，prolate spheroidal wave function)脉冲作为MIR UWB系统的基本子带脉冲，利用其在时域和频域的双正交特性，代替收发信机中的滤波器组，降低了系统实现的复杂度. 因此，笔者在此基础上，构建采用PSWF脉冲的并行组合脉冲MIR UWB通信系统.
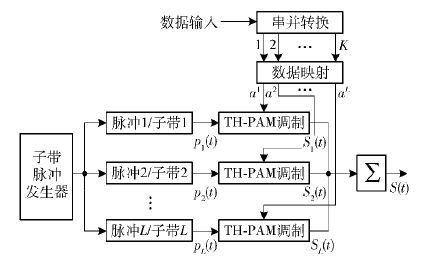
2 并行组合脉冲MIR UWB通信系统 2.1 发射机原理并行组合脉冲MIR UWB系统发射机原理框图如图 1所示，利用r-组合数据映射算法[7]选择与多个子带相对应的多个脉冲，以并行组合的形式传输数据信息.
 | 图1 并行组合脉冲MIR UWB系统发射机原理框图 |
在发送端，输入数据首先经过串/并转换，输出Kbit并行数据，然后根据r-组合数据映射算法，从L个脉冲(子带)中选择r个脉冲(子带)，并同时利用脉冲的不同极性来发送数据，则系统每次可传输的比特数为K=r+⌊lb(CLr)」bit，其中⌊ ·」为向下取整. 由此可知，当L值一定，r值较小时，K值会随着r值的增大而增大，信息传输速率也随之提高. 例如，当L=8，r=3时，K=8bit，与一个占用8个子带的常规MIR UWB系统传输的比特数相同，却只占用频带资源的3/8，大大提升了频谱使用效率. 但当r值大于某一数值，直至等于系统子带总数L时，K值会随之减小. 因为，当r值逐渐接近L值时，CLr的组合情况会逐渐减少，导致K值的减小. 所以，应根据实际传输速率的要求来选择合适的L和r取值.
数据映射部分的输出为ai∈{0,±1}，i=1,2,…,L，其中L为系统子带总数. 由r-组合数据映射算法可得，ai中将有r个取值不为0，表示选择对应序号的子带脉冲及其极性来承载发送数据；其余L－r个取值为0，表示未选择该子带对应的脉冲来承载发送数据. 之后，将ai送入相应的调制器中，各支路调制脉冲pi(t)由子带脉冲发生器产生，并采用PSWF脉冲.
最后，将各支路信号相加，得到发射信号为
S(t)=$\sum\limits_{i=1}^{L}{{}}$Si(t)=
$\sum\limits_{i=1}^{L}{\sqrt{{{\varepsilon }_{S}}}}\sum\limits_{j=-\infty }^{+\infty }{{}}$a⌊j/NS」ipi(t－jTS－Ci,jTC)
(1)
并行组合脉冲MIR UWB系统接收机原理框图如图 2所示.
 | 图2 并行组合脉冲MIR UWB系统接收机原理框图 |
假设系统同步已经完成，则接收信号为
r(t)=$\sum\limits_{i=1}^{L}{\sqrt{{{\varepsilon }_{S}}}}\sum\limits_{j=-\infty }^{+\infty }{{}}$a⌊j/NS」ipi(t－jTS－Ci,jTC)+n(t)
(2)
采用相关接收，本地提供L个相关模板信号为
vi(t)=$\sum\limits_{j=-\infty }^{+\infty }{{}}$pi(t－jTS－Ci,jTC),
i=1,2,…,L
(3)
将r(t)与各支路的相关模板信号相乘，再进行累积积分，第i个支路的输出结果为Ri，有
Ri=$\int{_{0}^{{{N}_{S}}{{T}_{S}}}}$r(t)vi(t)dt=
$\int{_{0}^{{{N}_{S}}{{T}_{S}}}}\sum\limits_{i=1}^{L}{\sqrt{{{\varepsilon }_{S}}}}\sum\limits_{j=-\infty }^{+\infty }{{}}$a⌊j/NS」ipi(t－jTS－Ci,jTC)×
$\sum\limits_{j=-\infty }^{+\infty }{{}}$pi(t－jTS－Ci,jTC)dt+
$\int{_{0}^{{{N}_{S}}{{T}_{S}}}}$n(t)$\sum\limits_{j=-\infty }^{+\infty }{{}}$pi(t－jTS－Ci,jTC)dt
(4)
(4)
利用PSWF脉冲的正交特性，式(4)可化简为
Ri=$\sqrt{{{\varepsilon }_{S}}}$ aiNS$\int{_{0}^{{{N}_{S}}{{T}_{S}}}}$n(t)$\sum\limits_{j=-\infty }^{+\infty }{{}}$pi(t－jTS－Ci,jTC)dt
(5)
由发射端的映射算法可知，只有r个支路有信号发送，则Ri之中只有r个包含信号分量，其余L－r个为噪声分量.
将Ri送入最大值/极性判决器，以确定收到的信号属于哪一支路，若有
|Ri|>|Rm|,m≠i,m=1,2,…,L－r
(6)
Pci=$\int{_{0}^{+\infty }}$[p(|Rm|<|Ri|)]L－rp(Ri)dRi$\frac{1}{\sqrt{2\pi }}\int{_{-\frac{\sqrt{{{\varepsilon }_{S}}{{N}_{S}}}}{{{\sigma }_{n}}}}^{+\infty }}$${{\left[ 1-erfc\left( \frac{x+\sqrt{{{\varepsilon }_{S}}}{{N}_{S}}/{{\sigma }_{n}}}{\sqrt{2}} \right) \right]}^{L-r}}{{e}^{-\frac{x2}{2}}}dx$
(7)
r个支路同时正确判决接收的概率为
Pc=(Pci)r
(8)
因此，接收机接收出错的概率为
Pe=1－Pc=1－(Pci)r
(9)
若忽略脉冲极性判决过程中的差错[8]，则系统最终的比特误码率为
Pb=$\frac{L}{2\left( L-1 \right)}$Pe≈$\frac{1}{2}$Pe$\frac{L}{2\left( L-1 \right)}\frac{1}{2}\left\{ 1-\left[ \frac{1}{\sqrt{2\pi }}\int{_{-\frac{\sqrt{{{\varepsilon }_{S}}{{N}_{S}}}}{{{\sigma }_{n}}}}^{+\infty }} \right]{{\left[ 1-erfc\left( \frac{x+\sqrt{{{\varepsilon }_{S}}}{{N}_{S}}/{{\sigma }_{n}}}{\sqrt{2}} \right) \right]}^{L-r}}{{e}^{-\frac{x2}{2}}}dx \right\}$
(10)
在加性高斯白噪声(AWGN，additive white Gaussian noise)信道和多径衰落信道条件下对系统进行仿真和性能分析. 仿真时，将超宽带的可用频带范围3.1~10.6GHz划分为15个带宽为500MHz的子带，脉冲重复周期为TS=12ns，脉冲持续时间为TP=4ns，跳时码片宽度为TC=4ns，采用TH 2PAM调制方式. 映射算法部分的参数设置如表1所示，并假设系统同步已建立.
|
表1 映射算法参数设置 |
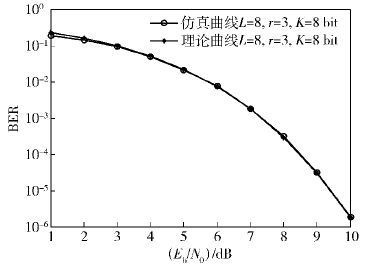
在上述仿真条件下，得到系统的比特误码性能的仿真曲线，并同时画出由式(10)所得的理论曲线，如图 3所示. 由曲线可知，系统的比特误码率随着信噪比的增加而降低，仿真曲线与理论曲线也基本重合，证明式(10)推导的正确性.
 | 图3 系统的比特误码性能的仿真和理论曲线 |
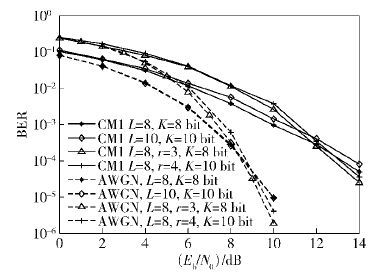
图 4所示为并行组合脉冲MIR UWB系统和常规MIR UWB系统在AWGN信道和多径衰落信道条件下的比特误码性能对比曲线.
 | 图4 并行组合脉冲MIR UWB系统和常规MIR UWB系统的比特误码性能对比曲线 |
由图 4中的曲线可知，在AWGN信道条件下的低信噪比时，常规MIR UWB系统的比特误码性能优于并行组合脉冲MIR UWB系统，但随着信噪比的增大，在大于9dB后，并行组合脉冲MIR UWB系统的比特误码性能开始优于常规MIR UWB系统. 这是由于常规MIR UWB系统的每个支路都是独立解调并恢复数据信息的，支路数量的变化对系统误码性能没有影响. 因此，图 4中的常规MIR UWB系统的2条性能曲线基本重合. 而并行组合脉冲MIR UWB系统的各个支路由映射算法相互关联，只有r个 支路同时正确判决，接收信息才能准确恢复. 在低信噪比条件下，r个支路同时正确判决的概率较低，因而导致并行组合脉冲MIR UWB系统的比特误码性能不如常规MIR UWB系统，但随着信噪比条件的逐渐改善，并行组合脉冲MIR UWB系统的性能也随之提升.
改变r的取值，当r=4时，并行组合脉冲MIR UWB系统每次发送的比特数增加为10bit，为了比较，令常规MIR UWB系统每次也发送10bit信息，则此时该系统的子带数目L=10，且系统的支路数也随之增加到10个，增大了系统硬件实现的复杂度. 如需进一步增大系统传输速率，常规MIR UWB系统则需要继续增加支路，而并行组合脉冲MIR UWB系统则无须增加支路，只需要通过映射算法调整r的取值即可，在系统硬件实现上体现出一定的优势.
在多径衰落信道条件下，仿真采用IEEE 802.15.3a信道模型(CM，channel model)1、多径分集(rake)接收和最大比合并方式. 由图 4中的曲线可知，在多径衰落信道条件下，2个系统的性能均差 于AWGN信道，且并行组合脉冲MIR UWB系统的比特误码性能在大信噪比时仍优于常规MIR UWB系统.
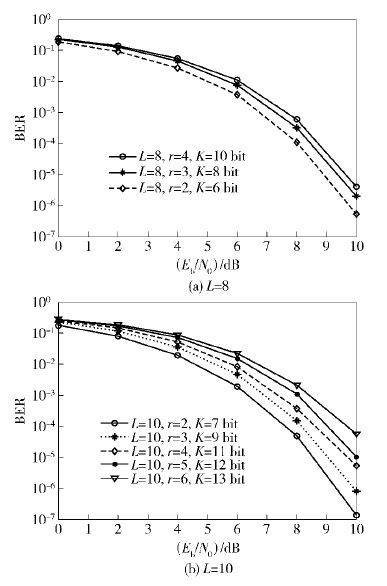
图 5所示为在L值相同、r值不同时系统的比特误码性能对比曲线. 由映射算法和图 5曲线可知，当L值确定、r值逐渐增大时，系统每次发送的比特数K会随之增加，传输速率也随之增加，但系统的比特误码性能却逐渐下降，这一结果也符合通信系统有效性与可靠性之间的矛盾关系. 所以，可根据系统对传输速率和比特误码性能的不同要求来选择适当的L、r等参数.
 | 图5 在L值相同、r值不同时系统的比特误码性能对比曲线 |
提出一种并行组合脉冲MIR UWB通信系统，给出系统发送端和接收端的工作原理及其框图，并进行系统性能的仿真. 结果表明，只发射部分子带脉冲，并行组合脉冲MIR UWB系统即可获得与常规MIR UWB系统相同的数据传输速率和接近的比特误码性能；且在大信噪比条件时，并行组合脉冲MIR UWB系统的比特误码性能开始优于常规MIR UWB系统. 同时，还可通过选择适当的映射参数来满足系统对传输速率和比特误码率等级的不同要求，为无线智能网络和无线传感器网络的物理层设计提供了一种可行方案.
| [1] | Win M Z, Scholtz R A. Impulse radio:how it works[J]. IEEE Communication Letters, 1998, 2(2):36-38.[引用本文:1] |
| [2] | Paquelet S, Aubert L M. An energy adaptive demodulation for high data rates with impulse radio[C]//IEEE Radio and Wireless Conference. Atlanta:IEEE, 2004:323-326.[引用本文:1] |
| [3] | Mittelbach M, Moorfeld R, Finger A. Performance of a multiband impulse radio UWB architecture[C]//The 3rd Conference on Mobile Technology, Applications and Systems. Bangkok:ACM, 2006:1-6.[引用本文:1] |
| [4] | Dehner H U, Figielek D, Jakel H, et al. High data rate coexistence-based channel coding for noncoherent multiband impulse radio UWB[C]//IEEE International Conference on Ultra-Wideband. Syracuse:IEEE, 2012:120-124.[引用本文:2] |
| [5] | 陈丽丽, 于欣, 窦峥. 采用椭球波脉冲的多波段超宽带性能研究[J]. 哈尔滨工程大学学报, 2014, 35(4):1-5. Chen Lili, Yu Xin, Dou Zheng. Research on the performance of multiband impulse radio UWB communication system based on PSWF[J]. Journal of Harbin Engineering University, 2014, 35(4):1-5.[引用本文:1] |
| [6] | Slepian D, Pollak H O. Prolate spheroidal wave functions, fourier analysis and uncertainty-I[J]. Bell Syst Tech J, 1961, 40(1):43-63.[引用本文:1] |
| [7] | 王玫, 郭黎利, 于奇. 基于改进r-组合映射编码并行组合扩频通信系统的分析[J]. 舰船电子工程, 2008, 28(10):78-81. Wang Mei, Guo Lili, Yu Qi. Analysis of coded parallel combinatory spread spectrum communication system based on improved r-combinatory mapping[J]. Ship Electronic Engineering, 2008, 28(10):78-81.[引用本文:1] |
| [8] | 朱近康. CDMA通信技术[M]. 北京:人民邮电出版社, 2001.[引用本文:1] |