针对遥感图像地形背景复杂的问题,提出分块鲁棒主成分分析的撞击坑候选区域自动提取方法.基于图像分块,采用交替方向乘子算法进行结构稀疏的低秩分解,低秩成分表示冗余相似的背景,稀疏成分代表包含潜在撞击坑的显著区域.针对显著的区域图采用数学形态运算分割获取候选的撞击坑图像,并通过对候选图像进行稀疏表示的分类,识别出真实撞击坑.基于火星和月球图像的实验结果表明,该方法能有效去除复杂地形和光照的干扰,检测率达到91.7%.
Crater is important for analyzing the relative dating of planetary and lunar surfaces. For the complex terrains in remote sensing images, a robust blocked principal components analysis (RPCA) approach was proposed to automatically detect crater candidate regions. An alternating direction multipliers algorithm was presented for RPCA based on the blocked planetary images. The background is modeled as a low-rank matrix, and the salient regions map is represented by structure sparse parts that contain potential craters. The crater candidates are obtained by mathematical morphological operations for the saliency regions map, they are precisely distinguished from falsely detected ones through a sparse representation classifier in feature space. Experiments on the images from Mars and Moon demonstrate show that the accuracy rate of crater recognition can reach up to 91.7% by effectively eliminating the effects of background and illumination.
陨石撞击坑又称撞击坑,是行星表面上最为常见的地貌特征,撞击坑提供了行星的地质年龄和地质进化历史的丰富信息[1]. 然而,高解析度图像中数量庞大,尺寸较小的撞击坑,其自动检测和计数仍然是有挑战性的问题[2].
特别是撞击坑的结构形态复杂多变,非均匀的光照变化引起图像灰度的显著变化,复杂的背景地形变化,如山脉、沟壑、起伏不定的地貌和光照变化噪声等. 最近,鲁棒主成分分析(RPCA,robust principal components analysis)对视频多帧图像分析显示了有效的矩阵低秩分解技术[3]. 笔者将低秩分解技术应用到撞击坑的检测算法中,突出撞击坑的显著特征,有效消除复杂地形背景对分割撞击坑图像的不利影响. 星表图像实验结果表明了所提出的基于矩阵低秩和结构稀疏分解算法的有效性和实用性.
1 撞击坑检测识别算法框架基于RPCA的显著性检测方法,提出了针对遥感图像的撞击坑检测识别方法. 该检测方法主要有4个步骤:背景去除和显著性目标检测,基于最大类间方差的图像二值化,撞击坑候选区域的分割,基于稀疏表示的精细撞击坑分类识别. 图 1为所提出方法的流程框图.
1.1 问题描述从认知科学的角度,图像的信息可以分成两个部分:背景部分和显著的目标[4]. 背景部分表示了冗余的信息,而显著突出的部分表示了图像中视觉注意的部分. 因此一幅图像可以在特征空间上表示为低秩矩阵和稀疏部分的组合,低秩矩阵可以解释为图像的背景,稀疏部分可以表示为显著突出的部分. 这是因为,占图像主体的背景可以认为一般处于典型的低维子空间,而视觉显著区域偏离了这一子空间,造成与其余部分的不同. 从子空间分析的角度,图像的视觉显著区域可以通过图像矩阵的低秩分解来得到,矩阵的低秩分解又称为RPCA[5].
对于单幅的行星遥感图像,撞击坑外形显示出粗造的圆形或圆环形,不仅在空间上是稀疏分布的,而且在视觉上是受到关注的部分,同时大量非突出的部分(背景)在结构或像素级别上是相似或相近的.与视频多帧图像所用的处理方法不同[4],单幅遥感图像可以表示为每一像素灰度值的矩阵形式,将其分割成互不重叠的小块图片,每一小块图片以其像素灰度级为元素值组成一列特征向量来表示. 将这些列向量顺序级联起来就构成图像的矩阵表示,即 I ={ p 1,p 2…,p n}∈$\mathbb{R}$m×n,其中元素 p i为每一分割小图像片的灰度值串接特征向量,m为特征向量的维数,n为分割数. 然后将其进行低秩分解,则有 I=H+B ,这里 H 表示低秩矩阵,包含具有相似或相近结构的背景部分,B 表示稀疏矩阵,矩阵所包含的小部分非零元素代表了图像视觉注意部分,包括可能的陨石撞击坑区域和一些突出的地貌单元. 矩阵的低秩分解可以表示为下面凸优化的求解问题:
| \[\begin{gathered} \mathop {\min }\limits_{B,H} = \gamma {\left\| B \right\|_1} + {\left\| H \right\|_*},\hfill \\ s.tI = H + B \hfill \\ \end{gathered} \] | (1) |
其中:‖H‖*表示矩阵的核范数,即矩阵的奇异值之和,表示矩阵的低秩度量;‖B‖1表示矩阵的l1范数,即矩阵元素的绝对值之和;γ>0为低秩和稀疏部分的平衡参数.
然而,RPCA进行矩阵分解时,稀疏正则化项将每一像素单独对待,没有考虑像素子集之间任何可能的关系或特定的结构. RPCA模型并不能显示出一个显著目标的像素单元在空间上分块聚集的特性. 对任意由行星或月球图像分块后所得到的观测矩阵而言,其数据矩阵只有很少的列向量之间是有明显不同的. 这些不同列向量的存在破坏了数据矩阵的低秩结构,因此这样的数据矩阵具有列稀疏的特征,而不是矩阵元素稀疏的特征. 这里提出一种新颖的低秩和结构稀疏的模型,表示为
| \[\begin{gathered} \mathop {\min }\limits_{B,H} = \lambda {\left\| B \right\|_{2,1}} + {\left\| H \right\|_*},\hfill \\ s.tI = H + B \hfill \\ \end{gathered} \] | (2) |
其中:‖·‖*也表示核范数运算,即矩阵的奇异值之和;‖B‖2,1= $\sum\limits_{i = 1}^n {\sqrt {\sum\limits_{i = 1}^m {{{\left( {{B_{i,j}}} \right)}^2}} } } = \sum\limits_j^n {} $( ||B j||)2称为矩阵的l2,1范数,这里 Bi,j是 B 的第(i,j)项,Bj指 B 的第j列.l2,1范数定义为矩阵各列向量 l2范数之和[8],用以刻画矩阵的一维意义下的稀疏度. 而λ>0用于平衡低秩项和稀疏项的效果.由于l2,1范数是鼓励矩阵 B 的列向量为零,即只有一些数据列向量被破坏,而其他的列向量保持原有的结构,是“干净”的数据向量. 采用‖B‖2,1可以确保矩阵 B 有精确的非零列向量,这些非零列向量表明是潜在的陨石撞击坑区域,这更符合图像分块的实际情况,有利于小撞击坑的检测. 最近,交替方向乘子(ADM,alternating direction of multipliers)法可以有效地求解一些凸优化的线性优化问题[6, 7]. 对式(2)的模型,提出基于ADM的高效求解算法.
2 基于ADM稀疏低秩分解算法 2.1 问题描述为了通过ADM算法求解式(2),构造相应的增广拉格朗日函数为
| \[L\left( {B,H,Y} \right) = \lambda {\left\| B \right\|_{2,1}} + {\left\| H \right\|_*} + \left\langle {Y,I - B - H} \right\rangle + \frac{\mu }{2}\left| {\left\| {I - B - H} \right\|} \right._F^2\] | (3) |
其中: Y ∈$\mathbb{R}$m×n为拉格朗日乘子,μ>0为惩罚参数,‖A‖2F=$\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {} } $|ai,j|2,〈·〉表示内积运算.ADM使用了两个简单子问题的分离结构求解最小化问题,以代替联合求解最小化的方法. 即分别对矩阵 B、H和乘子Y 进行最小化求解,求解后立即更新. 其问题可进一步描述为
| \[{B_{k + 1}} = \arg \mathop {\min L}\limits_B \left( {B,{H_K},{Y_K},\mu } \right),\] | (4a) |
| \[{H_{k + 1}} = \arg \mathop {\min L}\limits_H \left( {{B_{k + 1}},{H_k},{Y_k},\mu } \right),\] | (4b) |
| \[{Y_{k + 1}} = {Y_K} + \mu \left( {I - {B_{K + 1}} - {H_{k + 1}}} \right),\] | (4c) |
其中,子问题式(4a)的求解等价于求解如下问题:
| \[\mathop {\min }\limits_B \left\{ {\lambda {{\left\| B \right\|}_{2,1}} + \left( {\mu /2} \right)\left\| {\left( {1/\mu } \right){Y_k} + I - {H_k} - B} \right\|_F^2} \right\}\] | (5) |
记 Q =(1/μ) Y k+ I - H k,则下面的引理给出了关于稀疏误差矩阵 B 最小化问题的闭式解.
引理1 设 Q ∈$\mathbb{R}$m×n是给定的矩阵,Qj中j表示矩阵的第j列. 若求解下式:
| min B {λ‖ B ‖2,1+(μ/2)‖ B-Q ‖2F} | (6) |
其最优解为 B *,则 B *的第j列为
| [B *]j= Q jmax (1-λμ-1/‖ Q j‖2,0) | (7) |
子问题式(4b)可以重写为
| \[{H_{k + 1}} = \mathop {\min }\limits_H \left\{ {{{\left\| H \right\|}_*} + \frac{\mu }{2}\left\| {\frac{1}{\mu }{Y_k} + I\left| { - {B_{k + 1}} - {H_K}\left\| {_F^2} \right.} \right.} \right.} \right\}\] | (8) |
式(8)可以使用软阈值算子方便的求解[6],即 H k+1= USτ[∑]VT,τ=μ-1,核范数对应项进行奇异值分解( U ,∑,V )=SVD((1/μ) Y k+ I - B k+1),软阈值算子定义为 S τ(∑)=diag{(σi-τ)+},这里σi为第i个奇异值,diag指提取对角线上元素,t+为t的正数部分,即t+=max (t,0).
2.2 算法步骤图像分块的低秩分解算法充分利用了分块图像之间的相关性,低秩矩阵很好描述了性质相近的同类背景信息,稀疏误差矩阵反映了显著的撞击坑等目标. 考虑 l 2,1范数的基于交替方向的具体算法能够满足上述低秩部分的限制条件,有以下步骤.
0) 输入:图像分块所得矩阵 I 和设定参数λ;输出:低秩背景矩阵 H 和稀疏显著性矩阵 B.
1) 初始化. 计算初始的低秩矩阵 H 0和稀疏矩阵 B 0及拉格朗日乘子 Y 0:
| k ←0; H 0← I ; B 0←0; Y 0=sign( I )/J( I ),μ0>0,ρ>0 | (9) |
2) 求解矩阵 B k+1,即固定 H k阵,求解式(4a). 根据引理1,建立结构稀疏收缩算子得
| \[{B_{k + 1}} = CSV{T_{\lambda /\mu k}}\left( {\frac{1}{{{\mu _k}}}{Y_k} + I - {H_K}} \right)\] | (10) |
3) 固定 B k+1阵,求解矩阵 H k+1,即求解式(4b).
| \[\left( {U,\sum ,V} \right) = SVD\left( {\frac{1}{{{\mu _K}}}{Y_K} + I - {B_{K + 1}}} \right)\] | (11) |
4) 软阈值收缩:
| H k+1= U S (1/μk)[∑] V T | (12) |
5) 更新乘子:
| Y k+1= Y k+μk( I - H k+1- B k+1) μk+1=ρμk | (13) |
6) k←k+1,重复步骤2)~5),直至满足收敛条件式(15).
7) 输出最优结果:H*← H k,B *← B k.
这里,式(9)中J(·)表示矩阵对偶范数:
| J( D )=max (‖ D ‖2,‖ D ‖∞) | (14) |
循环收敛条件:
| ‖ I - B k- H k‖F/‖ I ‖F≤10-7 | (15) |
候选撞击坑区域的分割检测算法是对经低秩分解所得的显著图像进行二值化基础上运用数学形态算子进行分割. 显著图像有较高的峰值信噪比,通过最大类间方差法可以有效地进行图像二值化. 由于自然地貌的影响,图像中撞击坑的边缘总是不完整且存在空洞. 因此使用数学形态学的膨胀算子所用的结构元素形式,使得在光亮区域和阴影区域之间的空洞或间隙能够扩大或增厚形成以边缘为界的连通区域. 膨胀运算处理之后,相连接的物体可以根据形态学的8个方向的结构元素进行连通检测,获得潜在的撞击坑区域. 最终的撞击坑候选子图块统一归一化为24×24像素大小的灰度图片.
撞击坑候选图片中存在着真实的撞击坑和不少伪撞击坑. 为进一步精细筛选,把撞击坑和非撞击坑作为一个两分类的问题,引入稀疏表示分类(SRC,spares representation classification)算法来甄别真伪[8]. SRC属于监督的分类学习算法,训练集包含了标注的真实的撞击坑图片和非撞击坑图片.
将候选的撞击坑图片作为测试图片,以其原始像素灰度作为特征向量. 基于SRC求解测试图片在整个训练集上的稀疏编码,然后根据稀疏系数重建测试样本与实际样本构成的残差来进行判别. 稀疏编码方法采用SLEP程序包实现(http://www.public.asu.edu/~jye02/Software/SLEP).
4 实验验证所提方法分别应用到火星探测的图像和高解析度的月球环绕的图片上,其遥感图像解析度分别为200 m/pixel和7 m/pixel. 火星图像来自于火星轨道器(MOC,Mars orbiter camera),月球图像来自于月球探测轨道器(LROC,Lunar reconnaissance orbiter camera).
图 2显示了利用新算法在火星图像上检测识别的分步骤实施过程. 在图 2中可以观察到,经过低秩分解算法处理后,复杂背景的去除与光照的均匀化,使得撞击坑特征在视觉上表现得非常显著(见图 2(c)). 在图 2(e)中候选撞击坑区域不仅包含了视觉明显的撞击坑,还包含误检测的特殊地形. 经过监督的SRC分类算法,有效降低了候选撞击坑图像子块中误检项,达到了精细分类识别的目的. 最终的结果表明,算法类似于人类视觉的感知.
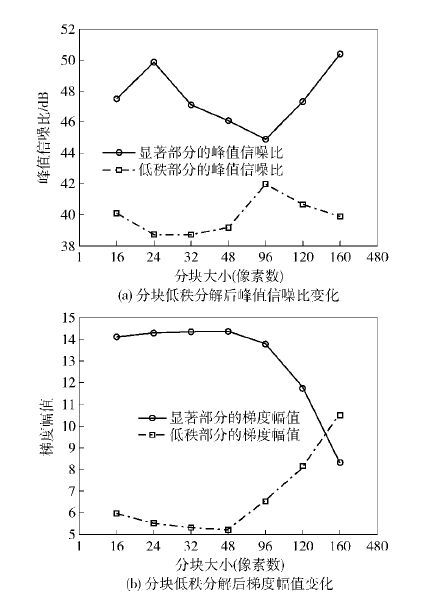
为了客观评价分块的低秩分解方法对撞击坑检测性能的提高,图 3显示了在星表图像中分块大小对低秩分解后的图像质量变化曲线,其视觉质量指标包括峰值信噪比和表示图像清晰度的梯度幅值,这两个指标值越大意味着更好的性能. 由图 3可以看出,低秩分解所得的显著撞击坑图像的指标都远高于低秩部分的指标,表明低秩分解后,图像的可视质量有了很大提高,突出了撞击坑目标,显著提高了其检测效果. 最佳的子块大小为24×24像素,分解所得的显著撞击坑图像的信噪比指标达到最大峰值,而梯度幅值都处于较大值. 随着子块大小的增加,图像质量逐渐下降,这是由于分块图像中的相似性逐渐降低,导致低秩分解所获得的稀疏显著部分比重减小所致.
本实验是在480×480大小的103幅星表图像进行撞击坑的检测识别,所包含的火星和月球图像中涉及不同的光照、尺度、地形条件下的1 069个陨石坑. 图 4分别显示了所提方法在火星MOC图像和月球LROC图像上的检测结果.
5 结束语针对遥感行星图像地形复杂,光照变化大的特点,提出了分块RPCA的撞击坑检测方法,包括ADM的低秩分解的算法和撞击坑候选区域提取方法,并引入了稀疏表示的精细分类方法. 对火星图片和月球影像的实验结果表明,低秩分解可以有效去除地形背景的干扰,稀疏矩阵可以很好表示显著的撞击坑区域. 统计103幅火星和月球星表图像检测结果,撞击坑的检测率达到91.7%,相比于采用中值滤波再进行阈值分割检测撞击坑的方法[2]检测率提高了17.4%.
| [1] | Jin Shuanggen, Zhang Tengyu. Automatic detection of impact craters on Mars using a modified adaboosting method[J]. Planetary and Space Science, 2014, 99(9):112-117.([引用本文:1]) |
| [2] | Urbach E R, Stepinski T F. Automatic detection of sub-km craters in high resolution planetary images[J]. Planetary and Space Science, 2009, 57(7):880-887.([引用本文:2]) |
| [3] | Candes E J, Li Xiaodong, Ma Yi, et al. Robust principal component analysis[J]. Journal of the ACM, 2011, 58(3):111-1137.([引用本文:1]) |
| [4] | Yan Junchi, Zhu Mengyuan, Liu Huanxi, et al. Visual saliency detection via sparsity pursuit[J]. IEEE Signal Processing Letters, 2010, 17(8):739-742.([引用本文:2]) |
| [5] | Liu Guangcan, Lin Zhouchen, Yan Shuicheng, et al. Robust recovery of subspace structures by low-rank representation[J]. IEEE Trans. on Pattern Analysis and Machine Intelligence, 2013, 35(1):171-184.([引用本文:1]) |
| [6] | Cai Jianfeng, Candes E, Shen Zuowei. A singular value thresholding algorithm for matrix completion[J]. SIAM J. Optimization, 2010, 20(4):1956-1982.([引用本文:2]) |
| [7] | Yang Junfeng, Zhang Yin. Alternating direction algorithms for 1-problems in compressive sensing[J]. SIAM Journal on Scientific Computing, 2011, 33(1):250-278.([引用本文:1]) |
| [8] | Wagner A, Wright J, Ganesh A, et al. Toward a practical face recognition system:robust alignment and illumination by sparse representation[J]. IEEE Trans. on Pattern Analysis and Machine Intelligence, 2012, 34(2):372-386.([引用本文:2]) |