2. 黑龙江大学信息科学技术学院, 哈尔滨 150080
提出了基于动态环结构的移动目标信息收集方法.首先通过选择骨干节点在网络内构建动态环结构;然后建立骨干节点和普通节点之间的依赖关系,并形成骨干路径,实现目标位置信息在网络内部处理、传输并最终发送给sink;最后通过模拟实验验证了该方法的有效性和优越性.
2. School of Information Science and Technology, Heilongjiang University, Harbin 150080, China
A circular structure based target information collection algorithm was presented, which constructs a dynamic circles structure by selecting backbone nodes. The algorithm further constructs the dependencies between backbone nodes and normal nodes to form the backbone path. The target location information was processed and forwarded in networks. Finally, the performance of the proposed algorithm was analyzed.
移动目标跟踪是无线传感器网络的一个重要研究问题[1],如何高效地收集目标感知数据并处理是研究的关键. 现有目标信息数据收集方法大都关注如何有效地将感知数据信息发送到sink,这会导致大量的网络能量消耗[2, 3, 4, 5, 6, 7, 8]. 针对传感器网络能源有效的特性,笔者研究基于动态环结构的目标信息收集方法,通过选择骨干节点在网络内构建动态环结构,实现网络内目标定位和能源节省的信息收集,最后通过实验验证了所提出算法的有效性.
1 基于动态环的网络构建算法假设传感器网络布置在2维平面上,网络由m个传感器节点组成,传感器节点集合N={n1,n2,…,nm}. 节点均匀分布在监测区域内,每个节点知道自己和邻居节点的位置信息.任意节点ni的位置用2维坐标(xi,yi)表示.假设所有节点的通信范围和感知范围相同,定义为以R为半径的圆形. 整个网络被划分为多个环,每个环上选取若干个节点作为骨干节点,骨干节点负责网络内的信息传输.
1.1 骨干节点选择算法定义1 给定任意骨干节点ni和间距d=δR,节点ni的4个邻居转折点坐标为p1={xi,yi+d},p2={xi+d,yi},p3={xi,yi-d},p4={xi-d,yi}. 用集合P={p1,p2,p3,p4}表示邻居转折点集合. 其中,0 <δ<1.δ可根据网络内节点分布情况来设定. 用B表示骨干节点集合,A表示待处理节点集合. 初始阶段网络内只有1个骨干节点,即为中心节点,B={nc},A=B. 从中心节点开始选择骨干节点加入集合B,并构建网络的动态环. 具体如下.
1) 集合A内任意节点ni首先计算自己的邻居转折点P={p1,p2,p3,p4},如果pj∈P(1≤j≤4)在网络范围外,则将pj从集合P移出,ni向邻居节点广播P. 非骨干节点接收到广播消息不作处理. 骨干节点接收到广播消息后,分别计算自己与P内每个转折点pk(1≤k≤4)的距离,如果距离小于αR,说明pk附近已经有1个骨干节点,pk从集合P移出,将更新后的P信息反馈给ni,其中,0 <α<1.
2) ni从所有邻居节点接收到P,并做交集获得最终的集合P. 由于节点ni已知邻居节点位置信息,ni从邻居节点中为P内每个成员选取1个距离最近的节点作为候选骨干节点nk(1≤k≤4). ni向所有候选骨干节点广播消息为总线请求(BREQ,bus request),BREQ消息为1个四元组〈ci,ni,nc,li〉. 其中:ci为ni所在环号,ni为发出信息的节点号,nc为中心节点的位置,li为ni到中心节点的距离.
定义2 任意节点ni(ni∈N)的依赖节点为ni的邻居节点中环号最小的骨干节点.
当节点ni产生感知信息或收到其他节点传来的信息后,将信息传给对应的依赖节点.
3) 收到BREQ消息的候选骨干节点nk首先计算自己到中心节点的距离lk,如果lk>li,则nk标记自己是第ci+1环上的骨干节点,B=B∪{nk},A=A∪{nk}-{ni}. 同时,nk选择ni作为依赖节点. 否则,说明nk在ni与中心节点之间,即nk在环ci内部,则nk将收到的信息丢弃,更新集合A=A-{ni}.
4) 重复执行步骤1)~3),直到A集合为空. 算法结束.
1.2 骨干路径建立算法当目标出现在网络中的任意位置,周围感应到目标的传感器节点将感知数据发送到骨干节点,骨干节点再将感知数据转发给中心节点. 中心节点收集感知数据后,对目标进行定位,并将结果发送给sink. 在这一过程中,包括2类路径,即骨干节点转发数据到中心节点,中心节点将定位结果传送到sink. 下面将详细介绍每个路径的构建过程.
1.2.1 骨干节点与中心节点间的骨干路径首先为非骨干节点选定依赖节点.
1) 所有骨干节点广播依赖请求消息为设备请求(DREQ,device request),DREQ消息为1个二元组〈ni,ci〉. 其中:ni为发出信息的节点号,ci为ni所在环号.
2) 如果普通节点收到多个DREQ信息,则选取环号较小的骨干节点作为依赖节点.
所有节点感应到目标或接收到其他节点的信息后,都将目标的信息传给各自的依赖节点. 重复这一过程,直到所有信息到达中心节点.
1.2.2 中心节点与sink间的骨干路径为了在保证信息传输的同时降低网络能耗,从每层环上选取1个节点组成中心节点与sink间的骨干路径. 该骨干路径由中心节点将目标定位结果传送到sink经过的骨干节点集合. sink节点向它的依赖节点发送消息,依赖节点将消息再转发给自己的依赖节点,重复这一过程,直到数据包到达中心节点. 数据包从sink到中心节点依次经过节点的逆序就是中心节点与sink间的骨干路径.
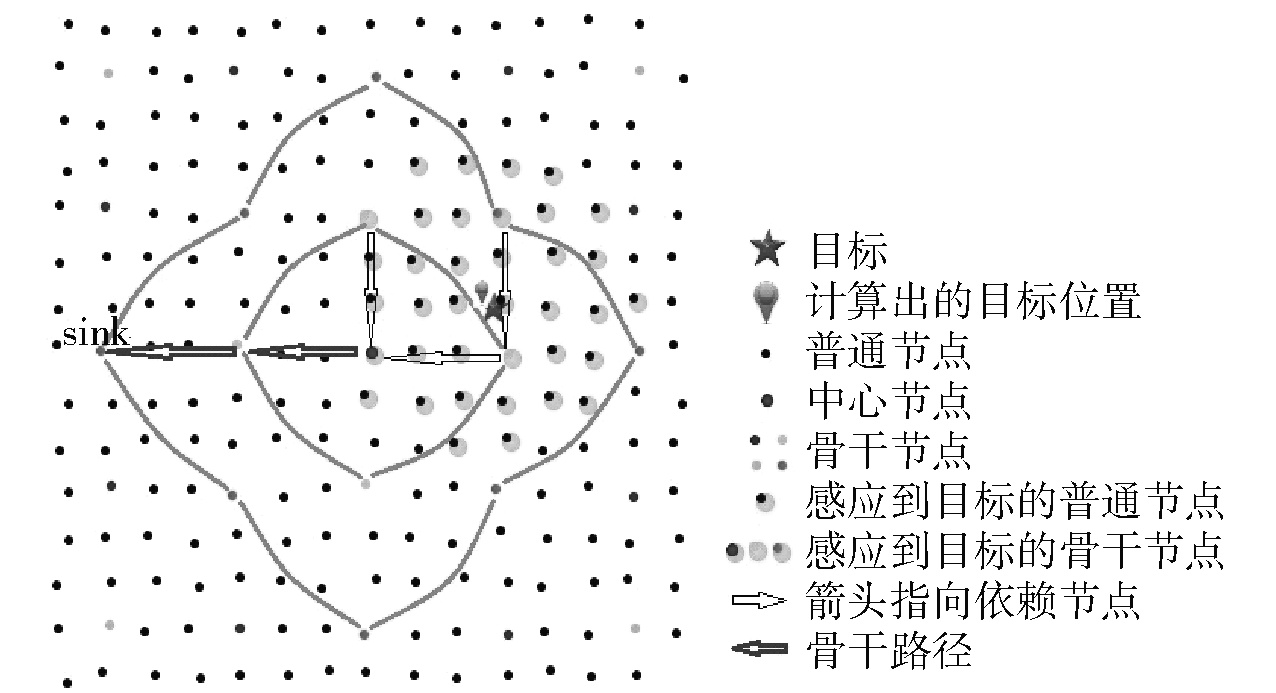
2 基于骨干网的移动目标跟踪算法 2.1 目标发现当目标进入网络监测区域内,位于目标周围的传感器节点能感应到目标,如图 1所示. 目标周围传感器节点发现目标,并测量节点与目标之间的距离,形成感知数据包DPacket. DPacket定义为1个三元组〈cdi,sdi,t〉. 其中:cdi为感应到目标的节点坐标(xi,yi),sdi为目标与发现目标的节点i的距离,t为感知到目标的时间.
2.2 目标信息融合发现目标的传感器节点将DPacket分别传输给自己的依赖节点. 接收到DPacket的骨干节点转发自己的依赖节点,依赖节点继续转发,此时DPacket将向环号较小的骨干节点转发. 重复这一过程,直到信息到达中心节点.
当DPacket全部到达中心节点之后,中心节点根据DPacket中的sdi数值,选出sdi值较小的m个节点,即距离目标最近的m个节点,作为参与目标定位的候选节点,计算出目标位置,形成定位节点数据包LPacket. 现有多数目标定位方法都可应用于所提算法 中,实验采用简单有效的加权质心算法. 目标的位置 坐标(Tx,Ty)为 Tx=$\sum\limits_{i = 1}^m {{{{x_i}} \over {s{d_i}}}} /\sum\limits_{i = 1}^m {{1 \over {s{d_i}}}} ,{T_y} = \sum\limits_{i = 1}^m {{{{y_i}} \over {s{d_i}}}} /\sum\limits_{i = 1}^m {{1 \over {s{d_i}}}} $.
2.3 目标位置信息反馈在目标位置信息反馈阶段,中心节点将LPacket通过骨干路径转发给sink. 中心节点作为骨干路径的起始节点,将LPacket发送给骨干路径中第2个骨干节点的位置,中心节点可与骨干路径上的第2个骨干节点直接通信. 骨干路径上的第2个骨干节点再将目标位置信息传给第3个骨干节点,重复该过程,直到目标的位置信息到达sink.
3 实验结果下面通过模拟实验来评估算法性能. 用Java语言搭建一个无线传感器网络的模拟环境,节点均匀分布在800×800单位的区域内. 传感器节点的数量在500~730之间变化,默认值为729. 传感器节 点的感知半径在100~200之间变化,默认值为100. 实验中δ值设定在0.6~0.9之间变化,默认值为0.8. 实验将考察网络内节点数量、节点感知半径和δ值变化对算法性能的影响. 在考察某一实验参数对算法性能的影响时,其他实验参数取默认值.
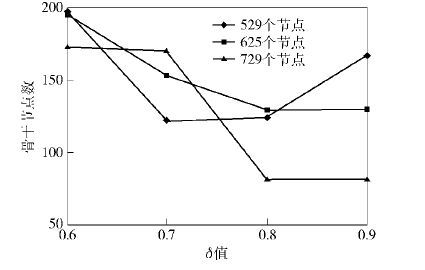
3.1 δ值对算法性能的影响下面讨论传感器节点数量在500~730之间变化时,δ值变化对算法性能的影响. 从图 2中可以看出,当δ值为0.8时网络中骨干节点数目最少. 但当网络中节点数为529,δ值为0.9时,骨干节点数量反而上升. 这是因为在进行选择骨干节点的步骤1)时,骨干节点接收到消息后计算自己与邻居转折点的距离,该距离虽然大于αR,但二者的距离依然很近,2个节点没有必要都成为骨干节点,这样整个网络就会产生一些不必要的骨干节点,所以此时应适当增加α的值.
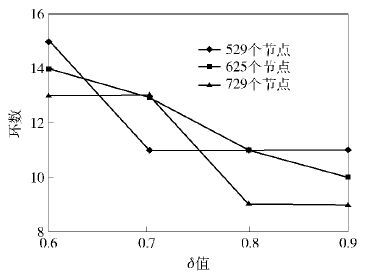
图 3为δ值不同时对应不同环数的示意图. 从图 3中可以看出,随着δ值的增大,环数减小,但小到一定数值则趋于稳定. 原因是在半径R固定的情况下,随着δ值增加,d=δR也增加,骨干节点之间的距离就随之增加,即环与环之间的距离增大,这导致网络内环数的减少. 而由于0 <δ<1,故0 <d <R,当d大到一定数值时,相邻骨干节点之间跨越的普通节点数量不再增加,即环与环之间的节点数量不会再增加,环数也趋于稳定.
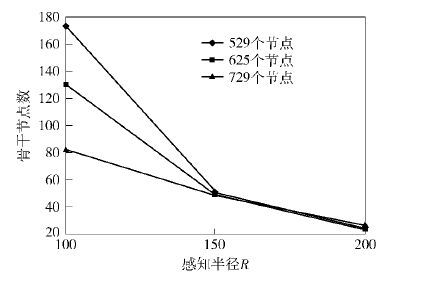
3.2 节点感知半径R对算法性能的影响在实验过程中,δ=0.8保持不变,改变感知半径的大小,分析节点数量对算法性能的影响.下面采用的感知半径分别为100、150、200. 图 4所示为在不同的节点数量下,感知半径变化对骨干节点个数的影响.当δ值固定时,d的大小只依赖于感知半径R的变化,且正相关. 随着感知半径R的增加,d数值变大,环数和骨干节点数量都减小.当节点平均距离相差不大时,环数不会有很大影响. 如果网络内的节点距离足够小,使距离中心更远而距离邻居转折点更近的节点存在,每个环向外扩展,才会导致总环数的减少.
在部署网络时应考虑,若可舍去距离目标远的节点感知到的信息,则尽可能选择感知半径大的节点,否则就要根据网络的具体情况,选择具有适当大小感知半径的节点来部署. 网络部署完成后,根据网络的规则程度,尽可能地增加δ值. 最终目的是减少环数,让信息以尽可能少的跳数到达sink.
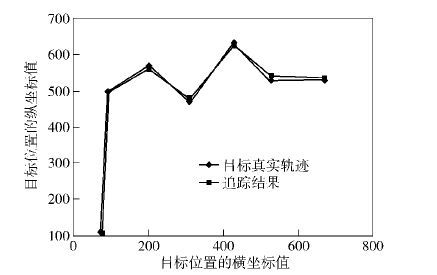
3.3 追踪精度下面讨论各参数对追踪准确度的影响. 如图 5所示,实验中选取任意7个目标位置的数据,通过改变参数值,对目标位置进行定位.当参数在合理的范围内变化时,选取距离目标最近的m个节点保持不变,所以随着参数的变化,定位数据不发生变化.对于任选目标的7个位置,定位误差在3.5~13.8之间变化,平均误差为7.221.
4 结束语笔者研究基于动态环的移动目标信息收集算法,在保证跟踪质量的同时减少网络能耗. 首先,给出基于动态环的无线传感器网络模型. 该模型从中心节点出发,递归选取各个环上的骨干节点,并制定了普通节点与骨干节点和骨干节点与骨干节点之间的依赖关系. 其次,将移动目标跟踪与基于动态环的传感器网络模型相结合,提出了有效的基于动态环的移动目标信息收集、处理方法. 该方法在收集信息的过程中融合数据,在网络内部直接计算目标位置,通过骨干路径传给sink. 再次,给出骨干路径构建算法,使中心节点将数据处理之后,通过最近的路径转发数据,提高通信效率. 最后,通过大量模拟实验,分析了各个参数对网络性能的影响.
| [1] | Chen Chiapang, Mukhopadhyay S C, Chuang Chenglong, et al. Efficient coverage and connectivity preservation with load balance for wireless sensor networks[J]. Sensors Journal IEEE, 2015, 15(1): 48-62. ([引用本文:1]) |
| [2] | Gao Yuhang, Niu Jianwei, Zhou Ruogu, et al. Zifind: exploiting cross-technology interference signatures for energy-efficient indoor localization[J]. INFOCOM 2013 Proceedings IEEE, 2013, 12(11): 2940-2948. ([引用本文:1]) |
| [3] | Alaybeyoglu A, Erciyes K, Kantarci A. An adaptive cone based distributed tracking algorithm for a highly dynamic target in wireless sensor networks[J]. International Journal of Ad Hoc and Ubiquitous Computing, 2013, 12(2): 98-119. ([引用本文:1]) |
| [4] | Piao Xinglin, Hu Yongli, Sun Yanfeng, et al. Correlated spatio-temporal data collection in wireless sensor networks based on low rank matrix approximation and optimized node sampling[J]. Sensors, 2014, 14(12): 23137-23158. ([引用本文:1]) |
| [5] | Villas L A, Boukerche A, Guidoni D L, et al. An energy-aware spatio-temporal correlation mechanism to perform efficient data collection in wireless sensor networks[J]. Computer Communications, 2013, 36(9): 1054-1066. ([引用本文:1]) |
| [6] | He Liang, Yang Zhe, Pan Jianping, et al. Evaluating service disciplines for on-demand mobile data collection in sensor networks[J]. IEEE Transactions on Mobile Computing, 2014, 13(4): 797-810. ([引用本文:1]) |
| [7] | 方效林, 高宏, 熊蜀光. 无线传感器网络高可靠低维护地理路由协议[J]. 通信学报, 2012, 33(5): 29-37. Fang Xiaolin, Gao Hong, Xiong Shuguang. RPR: high-reliable low-cost geographical routing protocol in wireless sensor networks[J]. Journal on Communications, 2012, 33(5): 29-37. ([引用本文:1]) |
| [8] | Lu Zaixin, Li Weiwayne, Pan Miao. Maximum lifetime scheduling for target coverage and data collection in wireless sensor networks[J]. IEEE Transactions on Vehicular Technology, 2015, 64(2): 714-727.([引用本文:1]) |