2. 国防科技大学信息系统与管理学院, 长沙 410073;
3. 国防科技大学并行与分布处理重点实验室, 长沙 410073;
4. 重庆市观音桥小学, 重庆 400020
针对多信道占空比感知无线传感网,证明了最低延迟广播问题是NP难问题,提出了两种新的概念:候选活跃冲突图和可行活跃冲突图,并在两种新概念的基础上提出了一种低延迟的广播算法——高效广播算法,理论分析证明该算法具有较小的近似比.仿真实验结果表明,与现有算法相比,高效广播算法能够有效降低广播延迟.
2. College of Information System and Management, National University of Defense Technology, Changsha 410073, China;
3. Science and Technology on Parallel and Distributed Processing Laboratory, National University of Defense Technology, Changsha 410073, China;
4. Chongqing Guanyinqiao Elementary School, Chongqing 400020, China
For multi-channel duty-cycled wireless sensor networks, the minimum delay broadcast problem was proved to be NP-hard. Two new concepts of candidate active conflict graph and feasible active conflict graph were presented. A Low delay broadcast algorithm called efficient broadcast algorithm was proposed based on these two new concepts. Analysis shows that this algorithm has a small approximation ratio. Simulation shows at the same time that efficient broadcast algorithm improves the broadcast delay efficiently compared with the existing work.
近年来无线传感网在许多领域得到了迅猛发展,如建筑结构健康状况监测、灾难恢复、环境监控和智能交通等. 无线传感网的节点通常由电池供电,因而节能是非常重要的问题. 因为睡眠机制可以显著节省传感器节点的能量,所以引起了学术界的广泛关注. 此外,与单信道通信技术相比,多信道通信技术虽然给算法设计增加了一定的复杂度,但是却可以减轻信号干扰的影响,特别是在稠密度无线传感网中可以有效地提高网络性能,因而也是研究者广泛关注的热点研究方向.
在无线传感网中,广播可用于将源节点的数据(路由信息、查询信息等)分发给所有其他节点. 在无线传感网的许多应用中,源节点的数据需要快速地传输给其他节点,因而广播延迟是无线传感网中非常重要的性能指标. 最低延迟广播问题已被证明是NP难问题[1],并且研究者提出了许多高效的算法[1, 2, 3, 4, 5]来解决该问题. 然而,大多数已有算法假设节点不休眠,或者假设节点只采用单信道进行通信. 在占空比感知场景中,节点只有在邻居节点醒来时才能传输数据给这些邻居节点. 此外,节点可以利用多信道通信技术来避免无线信号之间的干扰. 与笔者研究最相关的工作是Jiao等[6]提出的新近似广播(NAB,novel approximation broadcast)算法. 但是,文献[6]假设一个节点在一个调度周期中只醒来一次,从而不适合多次醒来的场景[7]. 因此,笔者研究如何在节点采用多信道通信并且可能多次醒来的场景中设计一种低延迟的广播算法.
文献[6]采用活跃干扰图来解决节点一次醒来条件下的广播问题,但是该活跃干扰图不能直接应用到传感器节点多次醒来的场景. 为了解决多次醒来场景下的广播问题,笔者首先证明了该问题是NP难问题,然后提出了两种新的概念:候选活跃冲突图(CACG,candidate active conflict graph)和可行活跃冲突图(FACG,feasible active conflict graph),用以刻画与接收节点活跃时间片相关的广播链路之间的干扰关系. FACG是在CACG的基础上遵循最小度优先规则构建的. 此外,笔者利用两种着色方法对FACG进行着色,并基于FACG和两种着色方法设计了一种低延迟的广播算法——高效广播算法(EBA,efficient broadcast algorithm),并证明了该广播算法的近似比为$2\left\lceil \frac{{{\chi }_{\alpha +1}}}{m\beta } \right\rceil $|T|, 其中α表示干扰半径与传输半径之比,m表示可用的信道数目,β表示一个节点在一个调度周期中的活跃时间片数目,| T |表示一个调度周期中的时间片数目,χλ为λ的函数,取值等于 $\left\lceil \frac{\pi }{\sqrt{3}}{{\lambda }^{2}}+\left( \frac{\pi }{2}+1 \right)\lambda +1 \right\rceil $ . 最后通过大规模的仿真实验对所提算法的性能进行了评估,仿真实验结果表明,与现有工作相比,EBA能够有效降低广播延迟.
1 系统模型考虑一种多信道占空比感知无线传感网,并将该网络建模为一个单位圆图G=(V,E),其中V表示节点集合,包含所有的传感器节点,E表示边的集合. 两个节点之间存在一条边,当且仅当它们之间的距离小于或等于传输半径. 采用协议干扰模型作为信号干扰模型,即当一个发送节点的接收节点处于其他发送节点的干扰范围时,该接收节点将由于信号干扰而无法正确接收其发送节点的数据. r 和rf分别表示传输半径和干扰半径,α表示rf与r之比,称为干扰比. 每个节点可以采用m个信道进行通信. Ch1、Ch2、…、Chm分别表示m个不同的信道.
假设整个调度时间划分为长度相同的调度周期. 一个调度周期T包含多个时间片0,1,…,|T|-2 和|T|-1,每个节点随机地从一个调度周期中选择β个时间片作为其活跃时间片. 在每个调度周期中,每个节点只有在活跃时间片才能接收数据,但是可以根据需要在任意时间片醒来发送数据. 占空比定义为节点的活跃时间片与整个调度时间之比,这里占空比等于 $\frac{\beta }{\left| T \right|}$.
2 低延迟广播算法 2.1 问题描述研究多信道占空比感知场景下的广播问题,其中一个源节点s在时间片0需要将它的数据广播给所有其他传感器节点. 当所有节点都接收到源节点数据时,广播任务才完成. 广播调度用于对每个节点的传输时间片和传输信道进行分配. 笔者研究的目标是如何最优化所有节点都能接收到数据时的延迟并且保证调度的数据传输信号之间互不干扰. 下面证明该问题是NP难问题.
定理1 所研究的问题是NP难问题.
证明 如果将β、|T|、α和m都设置为1,则所研究问题转换为单信道无休眠场景下的最低延迟广播问题,文献[1]已经证明该问题是NP难问题. 这里所研究问题的特例是NP难问题,因而本定理成立.
2.2 冲突图为了便于设计低延迟广播算法,提出了CACG和FACG的概念. 节点只有当其接收节点醒来时才能发送数据. 在一个调度周期中,一个节点可能醒来多次,因而其发送节点可以在其中任意一个活跃时间片进行数据传输.
针对需要调度的广播链路集合,按照下面的方式构造CACG. CACG包含多个冲突图. 对于所有链路接收节点的每个活跃时间片t,构造一个冲突图Gt=(Vt,Et). Vt中的每个节点对应一条满足以下条件的链路:该链路的接收节点在时间片t醒来. Et包含边的集合. 当两条链路之间存在干扰关系时,对应的冲突图中两个节点之间存在一条边.
因为数据传输只需要一个时间片,所以需要对每条链路分配传输时间片. 因此,在CACG的基础上按照节点最小度优先的顺序来构造FACG. FACG初始等于CACG,然后针对每个节点,寻找该节点所有冲突图中度最小的,在找到的冲突图中保留该节点,并从其他冲突图中删除该节点和相关联的边. 与CACG不同的是,一条链路只对应FACG中的一个节点. FACG中的边表示两个节点所对应的链路之间存在信号干扰关系.
2.3 算法步骤基于第2.2节讨论的CACG和FACG,提出EBA. EBA包括以下步骤.
1) 根据节点到源节点s的跳数将所有节点分到不同层中,包括L0、L1、…、LH,其中H表示所有节点到源节点s的最大跳数.
2) 因为最大独立集具有良好的几何属性,有利于设计高效的广播算法,所以逐层构造最大独立集. 为了方便论述,称最大独立集中的节点为黑节点. 构造过程从第L0层开始,L0层只包括源节点,所以将源节点设为黑节点. 在每一层中,选取黑节点的规则是,该节点不与已选黑节点相邻.
3) 基于构造的最大独立集来构建以源节点s为根的广播树. 该过程以逐层的方式来进行. 黑节点被指派为其他节点的父节点,黑节点的上一层节点被指派为黑节点的父节点,采用的规则为最小覆盖规则. 为了方便论述,黑节点的父节点被指派为蓝节点,除了黑节点和蓝节点之外的其他节点被指派为白节点.
4) 基于广播树逐层进行广播调度. 调度初始时间ts=0. 在每一层中,黑节点先广播数据,然后蓝节点再广播数据. 针对这些广播链路,首先构造CACG,然后根据节点最小度优先的规则构造FACG. 针对FACG,采用两种着色方法c和f来分配链路的传输时间片和传输信道.
首先对FACG的节点按照节点最小度最后的顺序进行排序,然后采用首次适配着色方法c对节点进行着色. 对于FACG中的每个节点v,将j设置为(c(v) mod m)+1,并将颜色值c(v)放入颜色集合Cj中. f(v)等于c(v)在颜色集合Cj中的索引值. 针对节点v对应的链路,调度该链路的传输时间片和传输信道分别为ts+(f(v)-1)|T|+i和Chj,其中i为FACG中对应的活跃时间片. 每个调度阶段结束时,调度时间ts前进到调度阶段结束后|T|的最小整数倍时间.
2.4 算法分析下面对EBA的近似比进行分析. 在分析近似比之前,首先分析两种着色方法c和f所需的颜色数目,然后分析EBA的最高延迟.
引理1 着色方法c所需的颜色数目最多为 $\left\lceil \frac{{{\chi }_{\alpha +1}}}{\beta } \right\rceil $ .
证明 在EBA调度的链路中,传输节点或者接收节点都是黑节点. 考虑构造的CACG. 假设黑节点v是最左边的黑节点. 如果其他黑节点与节点v相关的链路之间存在干扰关系,则这些黑节点必须是在以节点v为圆心内圆半径为r外圆半径为r+rf的半圆环中. 根据文献[8],这些黑节点的数目最多为χ(r+rf)/r-1=χα+1-1,因此,CACG子图的最小度最大为χα+1-1. 在最坏的情况下,CACG中的冲突图都是完全图,节点度最多为χα+1-1. FACG是基于CACG按照节点最小度优先的规则进行构造的. 因为每个节点具有β个活跃时间片,所以FACG中冲突图的节点度最多为 $\left\lceil \frac{{{\chi }_{\alpha +1}}-1}{\beta } \right\rceil =\left\lceil \frac{{{\chi }_{\alpha +1}}}{\beta } \right\rceil $-1. 着色方法c所需的颜色数目最多为该节点度加1,因而本引理成立.
引理2 着色方法f需要的颜色数目最多为 $\left\lceil \frac{{{\chi }_{\alpha +1}}}{m\beta } \right\rceil $ .
证明:着色方法f是基于着色方法c进行着色的. 根据引理1,着色方法c需要的颜色数目最多为 $\left\lceil \frac{{{\chi }_{\alpha +1}}}{\beta } \right\rceil $ . c分配的颜色被收集到m个颜色集合中,而f的着色值为这些颜色在每个颜色集合中的索引值. 因此,可以得到f最多需要 $\left\lceil \frac{{{\chi }_{\alpha +1}}}{m\beta } \right\rceil $ 种颜色数目.
定理2 EBA的最高延迟为2 $\left\lceil \frac{{{\chi }_{\alpha +1}}}{m\beta } \right\rceil $ |T|H-(2 $\left\lceil \frac{{{\chi }_{\alpha +1}}}{m\beta } \right\rceil $ -1)|T|个时间片.
证明 EBA逐层进行广播调度. 最顶层只有源节点s,因而L1层节点接收到源节点s广播数据的延迟最多为|T|个时间片. 在L1层,只有蓝节点是传输节点. 基于引理2,可以得到该过程最多需要 $\left\lceil \frac{{{\chi }_{\alpha +1}}}{m\beta } \right\rceil $ |T|个时间片.
从L2层到LH-1层,调度过程包括两个阶段. 在第一个阶段,黑节点广播数据,该阶段最多需要 $\left\lceil \frac{{{\chi }_{\alpha +1}}}{m\beta } \right\rceil $ |T|个时间片. 第二个阶段蓝节点广播数据,该阶段最多需要 $\left\lceil \frac{{{\chi }_{\alpha +1}}}{m\beta } \right\rceil $ |T|个时间片. 在最底层LH,只有黑节点是传输节点,该过程最多需要 $\left\lceil \frac{{{\chi }_{\alpha +1}}}{m\beta } \right\rceil $ |T|个时间片. 将所有过程的延迟进行组合,可以得到EBA的最高延迟为 |T|+2 $\left\lceil \frac{{{\chi }_{\alpha +1}}}{m\beta } \right\rceil $ |T|+$\sum\limits_{i=2}^{H-1}{{}}$2 $\left\lceil \frac{{{\chi }_{\alpha +1}}}{m\beta } \right\rceil $ |T|= 2 $\left\lceil \frac{{{\chi }_{\alpha +1}}}{m\beta } \right\rceil $ |T|H-(2 $\left\lceil \frac{{{\chi }_{\alpha +1}}}{m\beta } \right\rceil $ -1)|T| 因此,本定理成立.
定理3 EBA的近似比最大为2 $\left\lceil \frac{{{\chi }_{\alpha +1}}}{m\beta } \right\rceil $ .
证明 因为源节点的广播数据至少需要经过H跳到达所有的节点,而一跳数据传输至少需要一个时间片才能完成,所以可以得到所研究问题的广播延迟下界为H个时间片. 根据定理2,可以得到EBA的最高延迟为2 $\left\lceil \frac{{{\chi }_{\alpha +1}}}{m\beta } \right\rceil $ |T|H-(2 $\left\lceil \frac{{{\chi }_{\alpha +1}}}{m\beta } \right\rceil $ -1)|T|. 因为(2 $\left\lceil \frac{{{\chi }_{\alpha +1}}}{m\beta } \right\rceil $ -1)|T|大于0,所以通过比较最高延迟和广播延迟下界,可以得到本定理成立.
3 实验结果本节通过仿真实验来评估所提EBA的性能. 仿真实验采用Matlab平台来实现. 因为最相关的工作是Jiao等[6]提出的NAB算法,所以下面将在不同的大规模仿真环境下比较EBA和NAB算法的性能. 实验参数设置如表1所示.
| 表1 实验参数设置 |
实验设在长和宽都为100m的矩形区域,所有传感器节点随机部署在该区域中. 信道数目和干扰比分别固定为3和2. 实验中采用不同的网络规模、节点传输半径、调度周期|T|和节点活跃时间片数目β进行测试,并且在改变一个参数时固定其他参数.
实验在20个随机生成的拓扑上进行. 此外,针对每个拓扑进行10次实验,并且在每次实验时随机
选择一个节点作为源节点. 实验测试两个算法的广播延迟,即所有传感器节点接收到源节点广播数据所需要的总的时间片数目. 最终的实验结果为所有测试值的平均值. 对于NAB算法的实验,随机选择1个时间片作为节点的活跃时间片. 对于EBA的实验,分别随机选择2、3和4个时间片作为节点的活跃时间片.
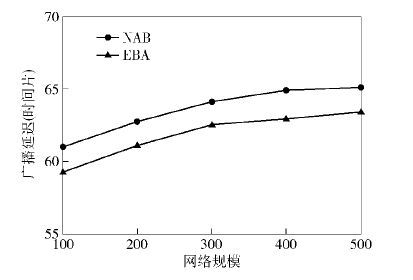
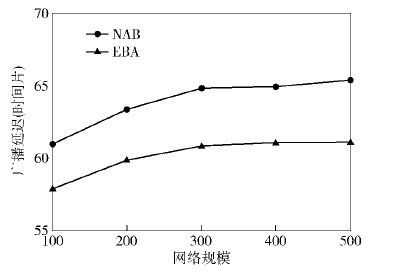
3.1 网络规模的影响下面测试不同网络规模对两个算法NAB和EBA性能的影响. 在实验中,将传输半径固定为30米,调度周期|T|固定为10,网络规模的取值从100增加到500,每次增加100. 实验结果如图 1~图 3所示.
随着网络规模的增大,源节点需要将数据传输给更多的节点,因而两种算法的广播延迟不断增加. 从图 1~图 3中可以观察到,在不同的网络规模下EBA的广播延迟都要低于NAB算法,而且在β增大时,优势更加明显. 主要原因是,EBA利用最小度优先的规则来构造FACG,从而许多链路被调度在不同的活跃时间片来进行数据传输. 当β增大时,一个接收节点在一个调度周期中醒来的次数增加,从而其传输节点完成数据传输的机会更多.
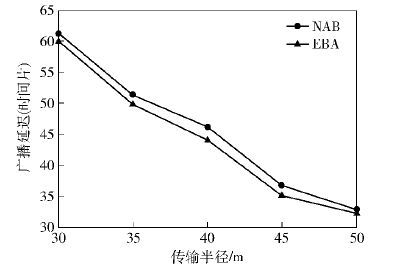
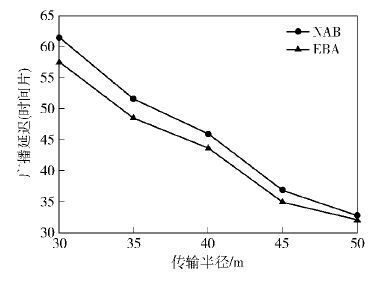
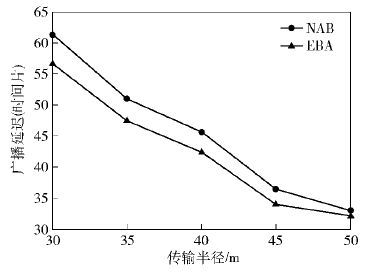
3.2 传输半径的影响下面测试不同传输半径对两个算法NAB和EBA性能的影响. 在实验中,将网络规模固定为300,调度周期|T|固定为10,传输半径的取值从30m增加到50m,每次增加5m. 实验结果如图 4~图 6所示.
随着传输半径的增大,传输节点可以覆盖更多的接收节点,因而两个算法的广播延迟不断减少. 从图 4~图 6中可以观察到,EBA的广播延迟要低于NAB算法,在传输半径比较小以及在β增大时,优势更加明显. 主要原因是,当传输半径比较小时,源节点的数据需要经过更多的转发才能传输给所有的传感器节点,而链路之间的信号干扰也随着转发次数的增加而增加. EBA利用FACG将存在干扰关系的数据传输链路分配到不同的活跃时间片来执行,从而能够有效地降低广播延迟. 当β增大时,EBA获得的分配机会更多,从而广播延迟也能不断降低.
4 结束语在多信道占空比感知无线传感网中,降低广播延迟是非常难的问题. 笔者提出的EBA可以根据接收节点不同的活跃时间片,对广播链路进行合理分配,然后利用着色方法将存在干扰关系的链路分配到不同的时间片或不同的信道上进行数据传输,从而能够显著降低广播延迟. 理论分析和仿真实验结果表明,EBA具有较小的近似比,并且有效地降低了广播延迟.
| [1] | Gandhi R, Parthasarathy S, Mishra A. Minimizing broadcast latency and redundancy in ad hoc networks[C]//MobiHoc. New York:ACM, 2003:222-232.[引用本文:2] |
| [2] | Gandhi R, Kim Y A, Lee S, et al. Approximation algorithms for data broadcast in wireless networks[C]//INFOCOM. New York:IEEE, 2009:2681-2685.[引用本文:1] |
| [3] | Hong Jue, Cao Jiannong, Li Wenzhong, et al. Sleeping schedule-aware minimum latency broadcast in wireless ad hoc Networks[C]//ICC. New York:IEEE, 2009:1-5.[引用本文:1] |
| [4] | Wang Feng, Liu Jiangchuan. Duty-cycle-aware broadcast in wireless sensor networks[C]//INFOCOM. New York:IEEE, 2009:468-476.[引用本文:1] |
| [5] | Xu Xiaohua, Cao Jiannong, Wan Pengjun. Fast group communication scheduling in duty-cycled multihop wireless sensor networks[C]//WASA. Berlin:Springer, 2012:197-205.[引用本文:1] |
| [6] | Jiao Xianlong, Xiao Weidong, Ge Bin, et al. On minimum-latency broadcast in multichannel duty-cycled wireless sensor networks[J]. International Journal of Distributed Sensor Networks, 2015, 12(1):1-8.[引用本文:3] |
| [7] | Han Kai, Liu Yang, Luo Jun. Duty-cycle-aware minimum-energy multicasting in wireless sensor networks[J]. IEEE/ACM Transactions on Networking, 2013, 21(3):910-923.[引用本文:1] |
| [8] | Wan Pengjun, Huang S, Wang Lixin, et al. Minimum-latency aggregation scheduling in multihop wireless networks[C]//MobiHoc. New York:ACM, 2009:185-194.[引用本文:1] |