2. 安徽理工大学经济与管理学院, 安徽淮南 232001;
3. 闽南师范大学计算机学院, 福建漳州 363000
数据稀疏性制约着协同过滤的推荐性能,为此,首先根据用户评分数量定义了用户的影响因子,在计算用户之间的相似性时,增加了影响因子衡量用户关系;其次,根据用户评分质量定义了有影响力用户群体.在此基础上,结合用户的评分数量和评分质量,使选择的有影响力近邻最大程度上作用于推荐过程.实验结果表明,所提方法能显著提高推荐性能.
2. School of Economics and Management, Anhui University of Science and Technology, Anhui Huainan 232001, China;
3. School of Computer Science, Minnan Normal University, Fujian Zhangzhou 363000, China
The recommendation performance of collaborative filtering is restricted by data sparsity. To solve this problem, the factor of user influence was thereafter defined according to the number of ratings to measure the relationship while calculating the similarity between users. Then, the influential user group was introduced according to the rating quality. On this basis, the chosen influential neighbor can work on the process of recommendations via combining the number of user ratings with the rating quality. Experiments show that the proposed method can significantly improve the recommendation performance.
协同过滤根据用户的评分、购买和评论等信息,为用户提供个性化推荐,却面临着数据稀疏性问题[1]. 许多研究人员提出了推荐算法来改善系统对稀疏数据的处理能力[2, 3, 4, 5]. 然而,面对数据稀疏的推荐环境,搜寻准确可靠的近邻仍然是提高系统性能的关键. 受社交网络中用户影响力概念启发[6],首先根据用户评分数量定义用户影响因子以改进传统的相似性计算;其次,根据用户评分质量定义有影响力用户群体;最后,综合考虑用户评分数量和评分质量,搜寻目标用户的有影响力近邻,以提高系统的推荐性能. 1 传统基于用户的协同过滤
传统方法首先进行相似性计算. 相关相似性(PCC,pearson correlation coefficient)的计算方法为
s(a,b)PCC=$\frac{\sum\limits_{i\in {{I}_{ab}}}^{{}}{\left( {{r}_{ai}}-{{{\bar{r}}}_{a}} \right)\left( {{r}_{bi}}-\bar{r} \right)}}{\sqrt{\sum\limits_{i\in {{I}_{ab}}}^{{}}{{{\left( {{r}_{ai}}-{{{\bar{r}}}_{a}} \right)}^{2}}}}\sqrt{\sum\limits_{i\in {{I}_{ab}}}^{{}}{{{\left( {{r}_{bi}}-{{{\bar{r}}}_{b}} \right)}^{2}}}}}$
(1)
然后选择与目标用户相似度较大的前k个用户作为其近邻. 最后,预测目标项的评分为
pti=${{{\bar{r}}}_{t}}+\frac{\sum\limits_{x=1}^{k}{s\left( t,x \right)\left( {{r}_{xi}}-\bar{r} \right)}}{\sum\limits_{x=1}^{k}{\left| s\left( t,x \right) \right|}}$
(2)
协同过滤本质上是选择与目标用户有类似兴趣爱好的用户作为近邻,然后利用近邻记录的评分信息预测未知评分. 然而,面对数据稀疏的实际预测环境,推荐结果往往与实际评分偏差较大. 因此,笔者提出了一种有影响力近邻的选择方法. 该方法通过同时考虑用户评分数量和评分质量来搜寻有影响力近邻,使目标用户近邻的选择更加准确可靠. 2.1 用户评分数量
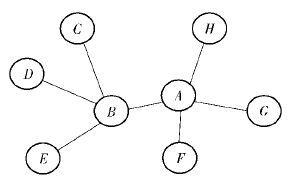
评分数量是有影响力近邻的一个衡量指标. 图 1所示的是由8个用户组成的简单用户关系网络,其中用户A为目标用户,用直线连接的2个用户具有共同评分项. 可以看出,A和B均和4个用户连接,这反映了A和B的评分数量相对较多,更容易与其他用户建立联系. 另外,考虑从B、F、G和H中选择A的近邻. 由图 1可知,F、G、H仅和A产生关系,以用户H为例,可得H的评分数量相对较少,导致H与A共同评分项较少. 根据少量共同评分项计算用户之间的相似性是不可靠的. 而B与多个用户都有关系,相比H,B和A计算得到的相似性更加准确可靠. 基于此,笔者根据用户评分数量定义用户的影响因子.
定义1 给定m个用户(m≥2),a和b表示其中任意2个用户,评分数量分别由qa和qb表示. 那么,基于用户影响因子的相关相似性方法定义为
s(a,b)=s(a,b)PCCδaδb
(3)
δa= $\frac{{{q}_{a}}}{\max \left( {{q}_{1}},{{q}_{2}},\cdots {{q}_{m}} \right)}$
(4)
在定义1中,所提方法反映了两两用户共同评分项的个数依赖单个用户的评分数量,一定程度上保证了与目标用户有更多共同评分的近邻的可靠性,且增加了近邻的评分推荐几率,使目标用户在近邻数较少时也能生成合理推荐. 总之,该方法考虑了共同评分项这一关键因素,同时强调了用户的评分数量影响共同评分项的个数,对于搜寻与目标用户相似度高且评分数量多的有影响力近邻具有重要的作用.
例如,给定一个包含5个用户对10个项目评分的实际用户评分矩阵,如表1所示.
| 表1 用户—项目实际评分矩阵 |
其中用户u1设为目标用户. 利用PCC计算得到u1与u2~u5的相似度分别为0.8660、0.8182、1.0000、1.0000. 同样地,利用所提方法计算得到 用户之间的相似性分别为0.3849、0.5455、0.4444、0.5556. 由此,可得以下结论:1) 除去u5,根据PCC的计算结果,u1和u4的相似度最高,而所提方法计算得到u1和u3的相似度最高;2) 上述2种方法计算得到u1和u5的相似度均最高. 针对结论1),由于u3评分数量多,与u1的共同评分项也越多,因此相似性结果更加可靠,且相比u4有更大几率为未评分项推荐评分,验证了所提方法的优越性. 针对结论2),可以看出,u1和u5具有完全不同的偏好:u1倾向打高分,u5评分偏低. 对于上述问题,将在后续对用户u5进行处理. 2.2 用户评分质量
用户评分质量也是衡量有影响力近邻的一个重要指标. 为了搜寻评分质量高的用户作为有影响力近邻,首先提出项目平均评分线的概念.
定义2 给定n个项目(n≥2),i为其中任意一个项目. 设项目i的平均评分为vi,那么把L={v1,v2,…,vn}定义为项目平均评分线,$\bar{v}=\sum\limits_{i=1}^{n}{\frac{{{v}_{i}}}{n}}$ .
由于真实世界中用户规模庞大,项目平均评分线能反映大多数用户对各项目的评分偏好,进而引入均方差以准确地衡量用户评分质量.
σa= $\sqrt{\sum\limits_{p\in {{W}_{a}}}^{{}}{\frac{\left( {{r}_{ap}}-{{v}_{p}} \right)}{\left| {{I}_{a}} \right|}}}$
(5)
定义3 均方差较小的α个用户组成有影响力的用户群体X. 另外,给定一个用户b,其平均评分${{{\bar{r}}}_{b}}$为b×X. 若${{{\bar{r}}}_{b}}$≥${\bar{v}}$,则为b×Y,其中Y为倾向打高分的用户群体;若${{{\bar{r}}}_{b}}$<${\bar{v}}$,则为b×Z,其中Z为倾向打低分的用户群体.
定义4 给定t为目标用户,用户c为其有影响力近邻. 若t×X,则c×X;若t×Y,则c×X+Y;若t×Z,则c×X+Z.
根据定义3和定义4,目标用户根据自身的评分倾向从对应的用户群体搜寻有影响力近邻. 另外,用户群体X中的用户有较高的评分质量,对目标用户未评分项的预测具有参考意义,故而X中的用户均有成为目标用户近邻的可能性. 具体地,由于用户u5倾向打低分,所以可排除在用户u1近邻选取范围以外,故u1的目标用户最近邻应该为用户u3(见表1). 另外,设置阈值α以调节有影响力的用户群体中用户个数对推荐结果的影响,实现提高近邻质量的同时,最大程度降低数据稀疏性影响的目的. 2.3 算法分析
根据2.1节和2.2节的分析,有影响力近邻选择方法的基本步骤描述如下.
算法:协同过滤中有影响力近邻的选择(INS-CF,influential neighbor selection in collaborative filtering).
输入:用户—项目评分矩阵,阈值α.
输出:目标用户t对未评分项i的预测评分pti.
步骤1 利用式(3)计算用户之间的相似性大小,然后获取用户之间的相似度矩阵 s ;
步骤2 利用式(5)计算用户评分的均方差;
步骤3 根据定义3选择α个均方差较小的用户组成有影响力的用户群体X,并得到倾向打高分用户群体Y和倾向打低分用户群体Z;
步骤4 根据目标用户t所在的用户群体,利用定义4确定其近邻选择范围;
步骤5 根据t与近邻选择范围内其他用户的相似性大小,选择与t相似度较大的前k个用户作为t的有影响力近邻;
步骤6 根据有影响力近邻的选择结果,利用式(2)预测目标用户对未评分项i的评分pti.
算法分析:所提算法综合考虑了用户评分数量和评分质量2个因素来选择有影响力近邻. 其中,前者在所提相似性度量方法中体现,而用户相似性的计算复杂度为O(m2),其中m为用户总数. 另外,用户评分质量的考量在于计算用户评分均方差和划分用户群体,其时间复杂度均为O(rm),r为常数. 由于传统协同过滤方法的时间复杂度为O(m2),故所提算法的时间复杂度并未提高. 3 实验结果及分析 3.1 数据集
为了验证所提算法的有效性,笔者选择公开的MovieLens数据集和Jester-data-2数据集进行实验(可在http://www.grouplens.org/下载). MovieLens数据集包含943个用户对1682个电影的评分记录;由于Jester-data-2数据集中的评分数据过于稠密,故只在其中随机抽取1852个用户在100个笑话上的评分记录. 数据集的详细信息如表2所示.
| 表2 数据描述 |
为了保证结果的无偏性,评分数据分为训练集和测试集,训练集占整个数据集的80%,余下20%数据作为测试集. 推荐过程采用五折交叉验证,测试集之间是互斥的,且有效地覆盖了所有评分数据. 3.2 评价指标 [7]
实验采用平均绝对误差(MAE,mean absolute error)和覆盖率来评价算法的推荐性能. MAE计算结果越小,算法的推荐性能越好;覆盖率越大,算法的推荐性能越好.另外,引入精度ηP和召回率ηR 2个评价指标进一步验证算法的有效性. ηP和ηR都是值越大,算法的推荐性能越好,计算公式分别为
${{\eta }_{P}}=\frac{1}{\left| U \right|}\sum\limits_{u\in U}^{{}}{\frac{\left| {{T}_{u}}\cap {{R}_{u}} \right|}{\left| {{R}_{u}} \right|}}$
(6)
${{\eta }_{R}}=\frac{1}{\left| U \right|}\sum\limits_{u\in U}^{{}}{\frac{\left| {{T}_{u}}\cap {{R}_{u}} \right|}{\left| {{T}_{u}} \right|}}$
(7)
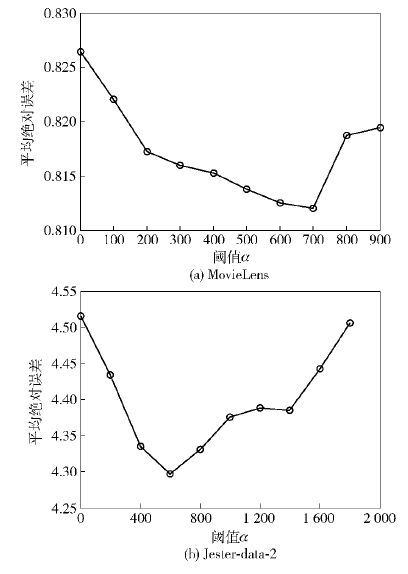
图 2展示了阈值α对推荐结果的影响(k取10).
随着阈值α的不断增加,MovieLens数据集上的MAE在[0,700]之间逐渐变小,而后增大,如图2(a)所示;类似地,Jester-data-2数据集上的MAE在[0,600]之间逐渐变小,而后增大,如图2(b)所示. 可以得出,α对推荐结果有影响. 当α设定过小时,存在评分质量高的用户未能充分用于评分推荐;当α设定过大时,倾向打高分或打低分的用户被错误划分到有影响力的用户群体,推荐质量反而下降. 因此,在后续实验中,MovieLens数据集阈值α取700;Jester-data-2数据集阈值α取600. 3.3.2 阈值α对推荐结果的影响
为了进一步验证所提算法的有效性,选取以下算法作为比较对象:基于余弦相似性的协同过滤算法(COS-CF,cosine-based collaborative filtering)[5]、基于相关相似性的协同过滤算法(PCC-CF,collaborative filtering based on pearson correlation coefficient)[6]和基于新的启发式相似性模型的协同过滤算法(NHSM-CF,collaborative filtering based on new heuristic similarity model)[7].
实验结果如图 3所示. 图3(a)~图3(d)分别展示了不同算法在MovieLens数据集上的MAE、覆盖率、ηP和ηR 4项评价指标的变化情况. 可以看出,所提算法在4个评价指标上均有更好的推荐性能,且随着近邻数k的增多,所提算法的推荐性能越来越好. 另外,图3(e)~图3(h)展示了不同算法在Jester-data-2数据集上的推荐性能. Jester-data-2数据集中的评分数据在[-10,10]范围内连续,且项目规模偏小(仅100个项目),这对算法的适应性提出了更高的要求. 结果显示,所提算法在总体性能上占优. 随着近邻数k推荐项目的增多,所提算法在MAE和ηR 2个评价指标上都表现较好;当近邻数k≥60时,覆盖率保持在99%以上. 在ηP评价指标上,当近邻数k较小时,NHSM-CF的ηP最大;当近邻数k较大时,NHSM-CF的ηP反而不如传统算法;当近邻数k≥20时,所提算法优于其他3种推荐算法.
综上所述,根据所提出的有影响力近邻选择方法在上述2个测试数据集的表现,可以得出,所提算法能显著提高系统的推荐性能. 4 结束语
随着网络上的数据规模不断扩大,推荐系统在为用户提供个性化服务方面扮演着越来越重要的角色. 协同过滤是推荐系统中的一种成功且应用广泛的推荐技术,却面临着严峻的数据稀疏性问题. 因而,降低数据稀疏性对推荐结果的影响,有利于提高系统的推荐性能. 笔者首先分析了衡量用户影响力的2个重要指标,即用户评分数量和评分质量,然后设计并实现了一种有影响力近邻的选择方法. 该方法在用户之间的相似性度量和近邻选择上作了较大改进,在2个测试数据集上的实验结果表明,所提方法能提高系统对稀疏数据的处理能力,实现系统推荐性能的进一步提高.
| [1] | Adomavicius G, Tuzhilin A. Toward the next generation of recommender systems:a survey of the state-of-the-art and possible extensions[J]. IEEE Transactions on Knowledge and Data Engineering, 2005, 17(6):734-749.[引用本文:1] |
| [2] | Breese J S, Heckerman D, Kadie C. Empirical analysis of predictive algorithms for collaborative filtering[C]//In Proceedings of the 14th Conference on Uncertainty in Artificial Intelligence. Madison:USA, 1998:43-52.[引用本文:1] |
| [3] | Shardanand U, Maes P. Social information filtering:algorithms for automating word of mouth[C]//In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems. New York:USA, 1994:210-217.[引用本文:1] |
| [4] | Liu Haifeng, Hu Zheng, Mian A, et al. A new user similarity model to improve the accuracy of collaborative filtering[J]. Knowledge-Based Systems, 2014, 56:156-166.[引用本文:1] |
| [5] | 徐雅斌, 孙晓晨. 位置社交网络的个性化位置推荐[J]. 北京邮电大学学报, 2015, 38(5):118-124. Xu Yabin, Sun Xiaochen. Individual location recommendation for location-based social network[J]. Journal of Beijing University of Posts and Telecommunications, 2015, 38(5):118-124.[引用本文:2] |
| [6] | 吴信东, 李毅, 李磊. 在线社交网络影响力分析[J]. 计算机学报, 2014, 37(4):735-752. Wu Xindong, Li Yi, Li Lei. Influence analysis of online social networks[J]. Chinese Journal of Computers, 2014, 37(4):735-752.[引用本文:2] |
| [7] | Bobadilla J, Ortega F, Hernando A, et al. Recommender systems survey[J]. Knowledge-Based Systems, 2013, 46:109-132.[引用本文:2] |