为了实现带内模式下控制链路的快速升级,提出了基于目的节点对所需升级的配置进行划分的计算机制,通过对上行链路和下行链路的分析提出了将上下行链路基于统一的升级处理机制分别进行升级的方法.实验结果表明,提出的算法能在相对更短的时间内得到配置升级时各节点的优先级分布,并以更少的升级步骤完成升级,但是需要占用额外的流表空间.
In order to solve the problems which may be arised when the routing policy of control plane is updated in in-band mode, an update mechanism based on the destination oriented routing was proposed. The mechanism divides the update policy into subclasses based on the different destinations, and also separates the uplink routing from downlink routing based on the destination. A unified update algorithm was presented for the updating of both uplink and downlink of controlling traffic. Experiment shows that the proposed mechanism shows more efficient both in the computation time and in updating time, but some extra flow entries may be needed.
软件定义网络(SDN,software defined networking)是近年来在学术界和工业界都重视研究与应用的一种新的网络架构. 相对于传统网络,SDN由于其灵活性及包容性,需要更多的配置升级与调整. 考虑到SDN的数据转发面是一个分布式系统,需要从集中的控制器向分布式的交换机下发升级配置内容,因此如果不做任何处理直接下发升级内容,即使初始配置状态与目标配置状态能够保证正确,在向大量交换机下发配置升级数据包时也无法保证中间状态的正常.
虽然SDN控制器与数据交换机之间的控制路由可以是带外模式,但是在大范围部署网络时,带内模式的控制路由是更好的选择,然而带内模式下则需要考虑控制链路的路由配置升级问题.
1 带内模式控制路由升级问题 1.1 问题描述文献[1]对带内模式控制路由升级问题进行了研究,基于控制路径的定义,需要保证在给任意交换机Si下发升级命令时,控制器都有一条链路能够通达至交换机Si. 其解决方案是,基于每个交换机,将每个交换机的升级优先级标记为Pi(Pi为正整数),交换机集合X表示已经升级的交换机,交换机集合Y表示还未升级的交换机. 对每个交换机以及可能的从控制器到交换机的路径组合,都基于以下规则建立不等式,即在需要升级交换机Si的流表时,需要建立从控制器到交换机Si的通路,而此通路则由已升级的交换机集合X与未升级的交换机集合Y组成,如∀Si∈X,Pj<Pi;∀Sj∈Y,Pi<Pk.
通过对每个交换机建立不等式并建模为整数线性规划求解,能够求得可行解. 然而,需要对解空间进行排除求解,同时求出最优解需要排除大量次优解,需要消耗很多时间. 因此文献[1]中对多节点的拓扑设定了200s的计算时间,在此时间内的最优结果即被认为是最优解.
1.2 问题处理在SDN的带内模式下,控制器向单个交换机Si下发控制信号的控制链路是直接指向单个交换机Si的,其控制链路与其他交换机的控制链路可以明确区分开来. 可以将控制链路区分为以对应交换机为目标的单向链路以及以控制器节点为目标的有向树链路,并分别进行链路升级计算. 而从控制器到单个交换机的路径升级计算则可以通过基于无环的依存关系算法来求取.
如上所述,控制器向单个交换机Si下发控制信号的控制链路是直接指向单个交换机Si的,其控制链路与其他交换机的控制链路可以明确区分开来. 而从各个交换机至控制器的上行控制链路则指向控制器,交换机的上行数据在上行链路中并没有进行区分. 同时,上行链路与下行链路的流表是完全区分开的,所以笔者将带内控制链路的升级分为上行链路的升级与下行链路的升级,在升级时对上行链路的相应流表和下行链路的相应流表进行分别升级,同时保证对应的上下行链路不会造成丢包即可完成升级.
将交换机标记为Si,i是不同交换机的唯一ID,因为是带内模式,控制器是架设在某个交换机之上的,所以控制器也可由此交换机的标记所代表,在此可标记为C. 笔者将当前的网络拓扑抽象为一个无向图G,其中的节点Si标记为交换机Si,无向边标记为交换机之间的连通链路,则对交换机Si中的任一流表都可以表示为从Si节点开始指向下一个节点Si+1的一条有向边.
上行链路的升级:由于从各个交换机至控制器的上行链路流表都以控制器为目标,不需要区分所有交换机的数据,所以在图G中可以根据交换机的上行转发表生成一棵有向树,其中仅有一个根节点C为目的节点控制器,其他叶节点都仅有一条有向边指向其父节点. 对于需要升级的上行初始链路配置可生成有向树G0,对于升级后的上行目标配置可生成有向树G1. 同样地,标记每个交换机Si的升级优先级为ki,问题是能够得到各个交换机的ki,使得在升级过程中,任意交换机Si向控制器C连通的上行链路都能连通,交换机Si在任意时刻发送的数据包都有链路到达控制器C.
下行链路的升级:由于从控制器C到任意交换机Si的下行控制链路可以由到不同目的的交换机进行区分,所以在图G中可以根据流表的下行转发表生成从控制器C到任意控制器Si的有向通路. 同样地,除了目的节点Si为根节点,其他节点都有一条有向边指向对应父节点. 对于每个需要升级的交换机Si,都可以根据其下行初始配置生成有向通路G0,根据其下行目标配置生成有向通路G1,问题是能够得到各个交换机的ki,使得在升级过程中,控制器C向任意交换机Si连通的下行链路都能连通,控制器C在任意时刻发送的数据包都有链路到达交换机Si.
可见上述2个问题可以归结为一个问题:对于已有的网络初始配置G0、目标配置G1,G0、G1都只有一个根节点,多个叶节点,如何配置每个节点Si的升级优先级ki,使得在任意时刻,G0或G1中的任意节点都有链路通向根节点.
2 求解算法 2.1 算法步骤按前文所述,笔者提出了一种新的机制:将上行链路与下行链路分开,根据目的节点将转发配置进行区分后分别计算基于目的节点的各节点流表的升级顺序. 由于上行链路的目的节点仅有控制器,所以转发表中仅需一条流表. 而下行链路则需要计算出各个流表的优先级顺序后,将所有的流表根据相同的优先级进行划分,然后将同一个交换机内相同优先级的流表进行合并,再根据优先级顺序下发升级流表,以减少流表空间的使用.
当目的节点确定时,对该目的节点所对应的初始配置和目标配置,获取所有需要升级的转发节点的优先级的值,同时需要确定升级过程中任意转发节点在任意时刻都有通向根节点的有向通路. 基于此需求提出了一种快速升级算法,它能够满足上述条件获得相应节点的优先级值,算法的具体步骤如下.
输入: {初始配置: original policy},{目标配置: target policy},目的节点集合: Destination
输出: 流表升级顺序: network update
1) for d in Destination:
2) generate directed graph G0 from original policy,and G1 From target policy.
3) generate directed graph Gu from the union of G0 and G1.
4) If SCC(strongly connected components) exists in Gu.
5) Do: update algorithm for the loops
6) Else Do: update algorithm for no loop
7) End if
8) for each Si:
9) Merge the flow-entries with the same ki
10)End for
11) End for
12)
13) update algorithm for no loop (G0,G1,Gu)
14) for Si in Gu:
15) if Si in G0.
16) ki=1;
17) Else:ki=0;
18)
19) update algorithm for the loops(G0,G1,Gu )
20) reference algorithm
强连接度存在性判定:由前文可知,对已确定的目标转发节点d,可生成初始配置有向图G0、目标配置有向图G1,G0、G1是无回环的有向图,合并G1与G0,得到其并集图Gu,因此图Gu中包含了所有从初始配置G0到目标配置G1可能的节点升级组合. 通过Tarjan算法判定Gu中是否存在1个节点以上的强连通分量.
若不存在1个节点以上的强连通分量,则说明图Gu中不存在环路,从而可以使用以下的升级机制来进行转发节点的升级.
无环升级机制:对于从初始配置G0升级到目标配置G1,当G0与G1的并集Gu中不存在环路时,说明以任何顺序升级Gu中的节点都不会出现环路,则通过以下2个步骤即可完成升级.
1) 对于任意节点v∈V(G0)-V(G1),升级所有节点v.
2) 同时升级除了已升级的节点之外的所有需要升级的节点.
可以证明无环升级机制能够保证在升级过程中的任意时刻图Gu中的任意交换节点都存在有向通路指向根节点.
由于上行链路是存在多个叶节点指向根节点的有向树,在配置变化升级时可能会在对应的图的并集中出现环路,不能简单使用无环机制来进行升级. 而在下行链路中,由于是控制器C到指定交换机Si的单叶节点的单向通路升级,所以因为常见的原因,如有一条链路失效,或需要通过一个特殊节点(如包过滤节点、包检测节点等)从初始配置升级至目标配置时,初始配置与目标配置对应的图的并集并不会出现回环,但是考虑到可能存在多种情况,因此和上行链路一样采用完整流程对下行链路的配置变化进行升级.
若判断存在多节点的强连通分量,说明从初始配置到目标配置的升级过程中可能出现回环,则无法直接使用无环机制来进行快速升级,需要先对Gu中可能出现的环路进行解环才能进行下一步处理. 此时可以通过对当前的回环进行逐个消减的方式去环,也可以使用Mahajan等[2]提出的启发式算法对当前所有的节点优先级进行排序,具体算法如下.
有环的优先级求解:从初始配置G0开始,对每个节点在图G0中加入该节点的新的配置边,检查是否会引入回环,若不会则此节点为根节点,否则作为不明节点暂存. 处理完所有节点后,对所有的不明节点做以下处理:对非不明节点v,去掉节点v的初始配置边,再引入不明节点u的新的配置边,若此时节点u的升级并不会造成环路,那么根节点v则是节点u的父节点,同时节点u不再是不明节点. 重复上述处理直到没有不明节点. 通过上述处理得到的节点之间的关系树即为依存关系树. 而升级时则先升级父节点,再升级其子节点,并以此类推.
如前文所述,由于上行链路是存在多个叶节点指向根节点的有向树,即使因为很简单的原因,如避免使用某条链路,而需要升级上行链路时,也可能会造成环路. 所以不妨对于上行链路的升级和下行链路的升级同时分别进行升级优先级的计算,并且分别进行升级,只需保证升级过程中上下行链路都是无损通信即可.
2.2 算法分析与文献[1]基于交换节点的升级,在升级过程中对单个交换机的全部流表进行升级不同,所提算法将流表以不同的到达目标转发节点进行区分之后,再对单个的目标转发节点进行分别处理.
对下行流表来说,因为目标转发节点的不同会使流表不同,为了节约交换机中的TCAM(TCAM,ternary content-addressable memory)空间,需要对单个交换机上同一个优先级的下发流表进行流表整合,整合算法可以使用文献[3]的工作,相对于文献[1]直接升级单个转发节点流表的方法,所提算法在真实的升级部署时因为下行链路可能会使用链路聚合机制,所以在下行链路升级时由于可能在一个交换机上进行多次升级,会需要多条额外的流表进行处理,因此会影响交换机的TCAM空间使用. 同时也可能会造成其他问题,如带给交换机和控制器额外的处理压力、传输路径偏移问题等,需要进一步的研究.
对上行流表来说,由于目标转发节点是一致的,所以每个交换节点的流表只需一条即可,所提算法在升级时不会对上行链路的TCAM空间造成额外的浪费. 同样地,所提算法能够在更短时间内得出节点升级的优先级数据,无环时的时间复杂度为O(|V|+|E|),存在环路时的时间复杂度为O(|V|2).
3 实验仿真在仿真中使用了2个拓扑数据库,即the Internet2 OS3E 和带边权重的Rocketfuel ISP,笔者在Intel 2.5GHz 的OSX环境下使用python基于上述拓扑实现算法,实验中的任意2个节点之间的有向通路都是基于带权的最短路径算法. 初始路径由随机选择的源节点和目的节点生成,在上行链路中,随机选择一个节点为目的节点,即控制器节点,由其他节点生成到目的节点的最短路径,从而生成初始配置;在下行链路中,同样随机选择一个节点为源节点,即控制器节点,然后任意选择一个节点为目的节点,生成对该目的节点的最短路径为初始配置. 对于一个初始配置,随机选择该初始配置路径中的任意2个节点之间的链路并使此链路中断,然后基于同样的源节点与目的节点生成目标配置路径. 下面来分别讨论对于上行链路和下行链路的配置升级的实验情况.
实验主要关注的是上行链路的升级计算,如前文所述,下行链路可以根据目的节点不同分为多个点到点的有向链路的集合,对每个点到点的有向链路进行配置升级的优先级计算. 但是相比上行链路,下行链路的复杂性相对更低. 因为上行链路是由多个叶节点到同一个目的节点的有向树,在同样的升级配置条件下,上行链路的节点和有向边的数量比下行链路要更多,需要的计算更为复杂,所以以上行链路的计算所需时间来进行参照.
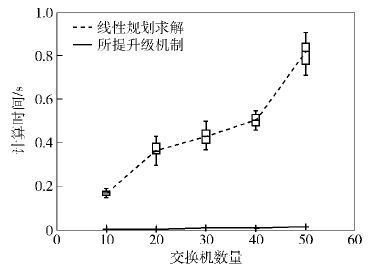
图 1所示为在从10个节点增加到50个节点,使得其中一半的节点需要升级的情况下,使用不同的升级机制所需要的计算时间,与预计的情况相似. 可见,由于节点的增加,线性规划约束条件也相应增加,使得解空间的求解与最优结果搜索需要大量的计算时间. 而所提算法通过分解问题并直接求解的方式,降低了计算难度,节约了求解的时间.
在不同拓扑规模下,实验统计了所需要的计算时间,选用的1239拓扑包括315个节点和1945条边. 随机选择每个拓扑下30%、60%及90%的节点作为需要升级的初始节点,并生成初始配置及目标配置,然后统计每次配置升级所需的时间. 随着拓扑数量级变大,所需要的计算时间增加,但是总是少于35ms,仍然在一个可接受的时间范围内.
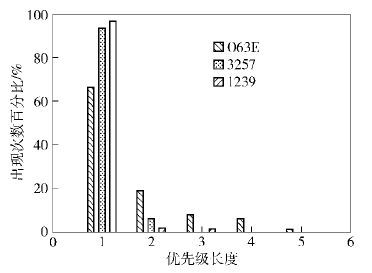
图 2所示为在3种拓扑下,分别生成初始配置和目标配置后,所计算出所需要升级的最高优先级值,即配置升级所需要的步骤,可见在90%的情况下,只需要3个步骤即可完成升级.
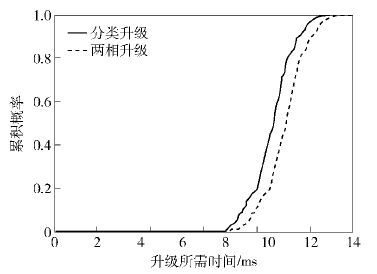
图 3中,将所提出的分类处理升级机制与目前通用的两相升级机制进行了实验对比. 与文献[4]的实验设置相同,将控制器与转发节点之间的时延设置为均值为4ms的正态分布,用于模拟数据中心中的网络环境.使用AS 1239,随机抽取50个节点作为所需升级的节点,以及1个控制节点,按照之前的实验设置生成需要升级的转发配置. 重复实验并测量了完成升级所需要的时间. 由于两相升级机制必须再次等待最大时延时间来保证所有的流表都已经图 3下发,而分类升级机制通过计算得到升级顺序之后即可进行流表下发. 图 3显示即使需要预计算,分类升级机制所需的完成升级时间依然稍好于两相升级机制,而文献[1]所需的计算时间过长,无法实现实时的升级计算. 实验证明所提分类算法可以获得比两相升级机制稍好的升级完成时间,同时不需要与两相升级机制一样在所有转发节点上使用双倍的流表空间.
4 结束语对带内模式下控制链路的配置升级问题,提出了一种新的升级机制. 新的升级机制基于目的节点将需要升级的配置进行分割,分别计算升级顺序并重新整合升级流表,能够在更短的时间里得到升级所需的流表优先级顺序,同时升级步骤更少,但是可能需要占用额外的流表空间,并对此机制进行了仿真,机制的性能符合预期.
| [1] | Zhang Shuyuan. In-band update for network routing policy migration[C]//2014 IEEE 22nd International Conference on Network Protocols (ICNP 2014).[S.l.]:IEEE, 2014:356-361.[引用本文:5] |
| [2] | Mahajan R, Wattenhofer R. On consistent updates in software defined networks[C]//2013 Proceedings of the Twelfth ACM Workshop on Hot Topics in Networks(HoTNets 2013).[S.l.]:ACM, 2013:20.[引用本文:1] |
| [3] | Kazemian P, Varghese G, McKeown N. Header space analysis:static checking for networks[C]//USENIX Symposium on Networked Systems Design and Implementation (NSDI 2012).[S.l.]:IEEE, 2012:113-126.[引用本文:1] |
| [4] | Curtis A R, Mogul J C, Tourrilhes J, et al. DevoFlow:scaling flow management for high-performance networks[C]//2011 ACM SIGCOMM Computer Communication Review(CCR 2011).[S.l.]:ACM, 2011:254-265.[引用本文:1] |