方向关系研究多针对简单空间对象,限制了空间关系建模的理论与应用研究.为此,基于定性方法,针对不确定区域间的方向关系表示模型,采用宽边界统一表示区域的不确定边界,利用基本主方向关系的组合描述不确定区域间的方向关系;在此基础上,定义不确定区域间的方向关系约束与约束满足问题,利用路径相容方法提出了一种不确定区域间方向关系的相容性检测算法,并分析了算法的推理复杂性,从而提出不确定区域间的方向关系推理模型.
As a fundamental spatial relation, the direction relations can describe position information between objects, which has been an important issue for spatial knowledge processing. Conventional researches mainly concern over the relations of simple objects, which restrict spatial relation modeling in further practical and theoretical research. The article focuses on the representation and reasoning models of direction relations of uncertain regions with qualitative methods. Firstly, an uncertain boundary was described using broad boundary model, and the direction relations between uncertain regions were represented with the combinations of basic cardinal direction relations. Moreover, through the representations, the direction relation constraints and satisfaction problem constraints or uncertain regions were defined. And a consistency checking algorithm was proposed for reasoning about the direction relations between uncertain regions, and the computational complexity of this algorithm was also analyzed.
空间关系建模主要研究空间对象的表示方法、对象间空间关系的表示方法与推理方法. 不确定性是现实世界的一种重要属性,在地质勘探、机器人导航、智能交通、图像处理等领域中都存在着具有不确定边界的空间对象,此类对象间的空间关系建模已引起广泛关注[1, 2]. 目前相关研究主要针对区域对象,且多针对空间拓扑关系,方向关系研究较少.
现有不确定区域间方向关系表示模型多是基于粗集和模糊集理论或是对已有精确模型(锥形模型、方向关系矩阵模型)的简单扩展. 在推理方面,目前多基于确定区域间的主方向关系[3, 4, 5, 6],不确定区域间方向关系推理研究尚处于起步阶段.
笔者针对具有不确定边界的区域对象,研究此类区域间的方向关系建模. 首先简要介绍主方向关系模型的相关定义;然后利用宽边界对不确定区域进行表示;基于确定区域间的主方向关系模型,采用组合方法描述不确定区域间的方向关系;在此基础上定义不确定区域间方向关系与约束,并研究不确定区域间方向关系约束规则;最后采用约束满足问题求解技术对不确定区域间方向关系进行推理.
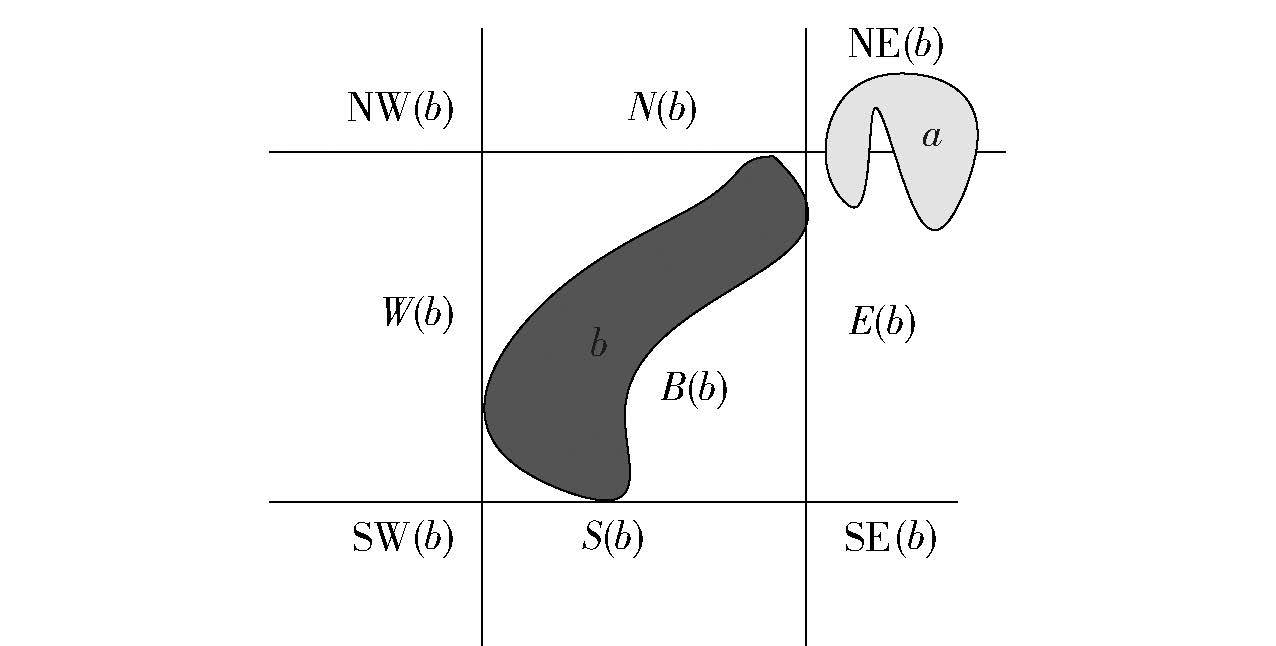
1 不确定区域间方向关系表示模型 1.1 主方向关系模型现有方向关系建模主要针对确定区域对象. 所有确定区域的集合用 $\Re $ [3]表示. 在描述确定区域a相对于b的方向关系时,称a为主区域,b为参照区域. 通过b的最小边界矩形(MBR,minimum bounding rectangle)为G(b),将平面空间划分成9个方向片,即B(b)、N(b)、NE(b)、E(b)、SE(b)、S(b)、SW(b)、W(b)、NW(b),分别表示b的中心、北、东北、东、东南、南、西南、西和西北方向,进而构成由区域b确定的参照系统π(b).
定义1 R=R1:…:Rk是一个基本主方向关系,如图 1所示. 其中:1) 1≤k≤9; 2) R1,…,Rk∈{B,S,SW,W,NW,N,NE,E,SE}; 3) 对每个i和j,若1≤i,j≤k,i≠j,则Ri≠Rj; 4)对任意一个参照区域b∈ $\Re $ ,存在区域a1,…,ak∈ $\Re $ ,其中a1∈R1(b),ak∈Rk(b)且a1∪…∪ak∈ $\Re $ [3].
基本主方向关系是由若干个方向片构成的表达式,表达式中方向片之间无顺序要求,例如B:E与E:B表示同一基本主方向关系. 特殊地,当k=1时,R1:…:Rk称为单片关系. 主方向关系模型共包含218个基本主方向关系,记为 U .
例如,图 1中的区域a位于b的东北和东方向,记为a NE:E b.
定义2 若一个基本主方向关系R为矩形关系,当且仅当存在2个矩形区域a和b,使得a R b[3].
定义3 R1=R11:…:R1n与R2=R21:…:R2m是2个基本主方向关系,若有{R21,…,R2m}⊆{R11,…,R1n},则称R1包含R2,记为R2⊆R1[3].
类似地,R1=R11:…:R1n是基本主方向关系,R2为方向片,若R2∈{R11,…,R1n},则称R1包含方向片R2,记为R2∈R1.
定义4 R为一个基本主方向关系,包含R的最小矩形关系(方向片数目最少)称为R的边界关系(BR,bounding relation),记为r(R)[3].
定义5 R为一个矩形关系,由R的最左方向片构成的矩形关系记为M(W,R). 类似地,可定义M(S,R)、M(N,R)、M(E,R)、M(NE,R)、M(NW,R)、M(SE,R)和M(SW,R). 特殊地,定义M(B,R)=R[3].
1.2 不确定区域表示方法导致空间关系具有不确定性的原因很多,例如人们认知的不确定性、空间对象属性(位置、边界等)的不确定性、信息采集和分析过程中的不确定性等. 笔者研究具有不确定边界的区域对象间的方向关系.
定义6 1个宽边界区域a由2个区域a1和a2组成,其中a1、 a2∈ $\Re $ ,a1∈a2. 将a1,a2分别称为a的内区域和外区域,a1、 a2的边界分别用 $\partial $ a1和 $\partial $ a2表示[7].
定义7 若a是1个宽边界区域,则a的宽边界记为Δa,其中Δa= $\partial $ a1∪ $\partial $ a2∪(a2-a1)[7].
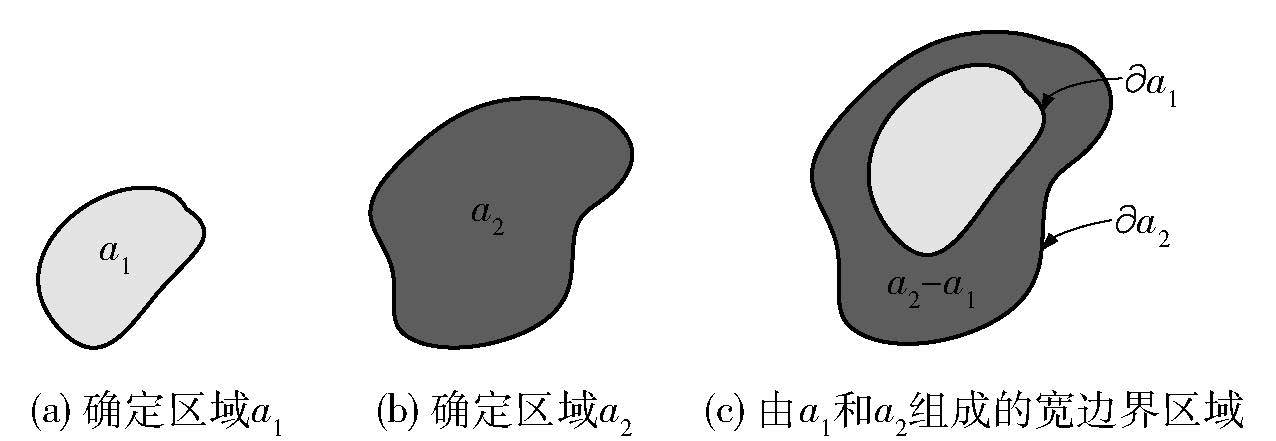
例1 图 2(a)和图 2(b)分别表示确定区域a1和a2,图 2(c)表示分别以a1、 a2为内、外区域构成的宽边界区域,2条边界和其间的深色部分表示区域的宽边界.
可用宽边界区域表示具有不确定边界的区域. 宽边界区域的外区域表示不确定区域的最大空间范围;内区域表示不确定区域的确定空间范围;外、内2个区域的差集和二者的边界表示不确定边界.
1.3 宽边界方向关系宽边界区域的内、外区域均为确定区域,因此可利用确定区域间的方向关系研究宽边界区域间的方向关系. 下面以218个基本主方向关系表示内、外区域间的方向信息,通过组合表示方法定义宽边界区域间的方向关系.
定义8 D=〈D1,D2,D3,D4〉为1个宽边界方向关系,当且仅当存在2个宽边界区域a和b,其中a1、 b1分别为a、 b的内区域;a2、 b2分别为a、 b的外区域,使得a1 D1 b1、 a1 D2 b2、 a2 D3 b1、 a2 D4 b2、 Di∈ U ,1≤i≤4.
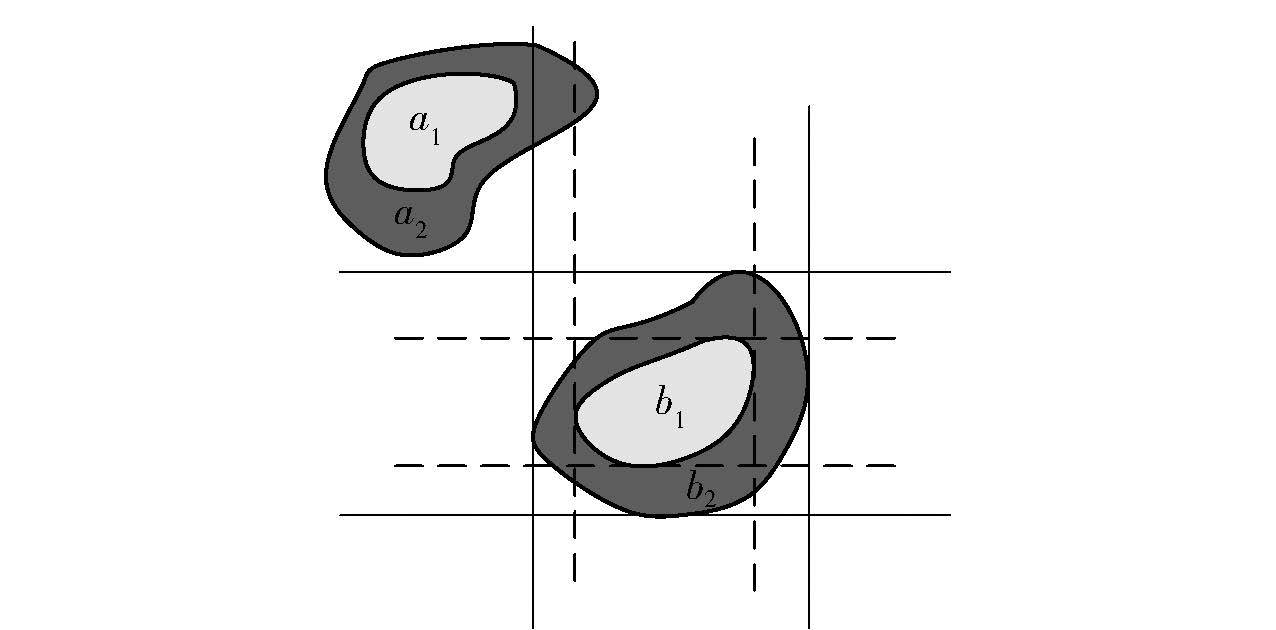
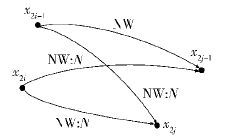
例2 如图 3所示,宽边界区域a(a1为内区域,a2为外区域)相对于宽边界区域b(b1为内区域,b2为外区域)的宽边界方向关系为〈NW,NW,NW:N,NW:N〉,记为a 〈NW,NW,NW:N,NW:N〉 b.
当a1=a2或b1=b2,即主区域或参照区域为确定区域时,a与b之间的方向关系可视为宽边界方向关系模型的特例,同样可用宽边界方向关系进行表示.
2 宽边界方向关系约束对于218个基本主方向关系,并非任意4个基本主方向关系的组合都可表示宽边界区域间的方向关系. 例如〈NW,NW,N:NW,NW:N:NE〉,不存在a1、 a2、 b1、 b2∈ R ,使得a1∈a2、 b1∈b2、 a2 N:NW b1、 a2 NW:N:NEb2同时成立,因此不是宽边界方向关系. 可见,若D=〈D1,D2,D3,D4〉为1个宽边界方向关系,则D1,D2,D3,D4彼此间存在约束. 对于任意一个宽边界方向关系,下面通过命题1~6给出其自身蕴涵的约束.
命题1 对于任一宽边界方向关系D=〈D1,D2,D3,D4〉,其中Di∈{D1,D3},方向片Rj∈{B,N,E,S,W},若Rj∈Di,则表达式(Rj∈Di+1)∨(B∈ Di+1)成立.
证明 对于满足关系D的任意2个宽边界区域a、b,分别设a1、b1为内区域,a2、b2为外区域. 当 Di=D1,方向片Rj=N且Rj∈D1时,得证(N∈D2)∨ (B∈D2).
由定义6和定义8可知,b1∈b2∧a1 D1 b1∧a1 D2 b2,根据基本主方向关系的形式化定义[3],有Ix(b1)≥ Ix(b2)∧Px(b1)≤Px(b2)∧Iy(b1)≥Iy(b2)∧Py(b1)≤Py(b2). 其中:I为函数值的下界(infimum);P为函数值的上界(supremum).
N∈D1,因此存在区域a′ 1∈ R ,a′ 1∈a1,使得a′ 1 N b1. 因此Ix(a′ 1)≥Ix(b1)∧Px(a′ 1)≤Px(b1)∧Iy(a′ 1)≥ Py(b1). 进而有Ix(a′ 1)≥Ix(b2)∧Px(a′ 1)≤Px(b2). 若Py(b2)≤Iy(a′ 1),则a′ 1 N b2,即有N∈D2;若Iy(a′ 1)≤Py(b2)≤Py(a′ 1),则a′ 1 B:N b2,即有N∈D2∧B∈D2;若Py(b2)≥Py(a′ 1),则a′ 1 B b2,即有B∈D2. 因此当Di=D1,N∈D1时,(N∈D2)∨(B∈D2)成立.
同理可证,对于Di∈{D1,D3},方向片Rj∈{B,N,E,S,W}的其他情况,相应的表达式(Rj∈Di+1)∨ (B∈Di+1)均成立. 综上,命题1成立.
命题2 对于任一宽边界方向关系D=〈D1,D2,D3,D4〉,有D1⊆D3,D2⊆D4成立.
证明 对于满足关系D的任意2个宽边界区域a、b,分别设a1、b1为内区域,a2、b2为外区域. 由定义8可知,a1 D1 b1∧a2 D3 b1. 设D1=R1:…:Rk,由基本主方向关系的定义,存在k个区域a11,a12,…,a1k,使得 a11∈a1,a12∈a1,…,a1k∈a1 a11∪a12∪…∪a1k=a1 且这k个区域分别位于方向片R1(b1),…,Rk(b1)中. a1∈a2,因此a11∈a2,a12∈a2,…,a1k∈a2,即a2存在k个子区域分别位于方向片R1(b1),…,Rk(b1)中,进而可知{R1,…,Rk}⊆D3,即有D1⊆D3.
同理可证,若D=〈D1,D2,D3,D4〉为1个宽边界方向关系,则有D2⊆D4. 综上,命题2成立.
定义9 R1=R11:…:R1n与R2=R21:…:R2m为2个基本主方向关系,R1∩R2={R11,…,R1n}∩{R21,…,R2m}.
命题3 对于任一宽边界方向关系D=〈D1,D2,D3,D4〉,其中Di∈{D1,D3},若{NE,E,SE}∩ M(E,r(Di))=∅,则{NE,E,SE}∩Di+1=∅.
证明 对于满足关系D的任意2个宽边界区域a、 b,分别设a1、 b1为内区域,a2、 b2为外区域. 当Di=D1,{NE,E,SE}∩M(E,r(D1))=∅时,得证{NE,E,SE}∩D2=∅.
由定义6和定义8可知,b1∈b2∧a1 D1 b1∧a1 D2 b2,因此有Ix(b1)≥Ix(b2)∧Px(b1)≤Px(b2)∧Iy(b1)≥Iy(b2)∧Py(b1)≤Py(b2). 若{NE,E,SE}∩M(E,r(D1))=∅,则NE(b1),E(b1),SE(b1)中不存在G(a1)的子区域,进而由基本主方向关系的形式化定义,可知Px(a1)≤Px(b1). Px(b1)≤Px(b2),因此Px(a1)≤Px(b2). 进而可知,NE(b2),E(b2),SE(b2)中不存在G(a1)的子区域,因此有NE$\notin $D2∧E$\notin $D2∧SE$\notin $D2,即有{NE,E,SE}∩D2=∅.
同理可证,当Di=D3,{NE,E,SE}∩M(E,r(D3))=∅时,有{NE,E,SE}∩D4=∅成立. 综上,命题3成立.
命题4 对于任一宽边界方向关系D=〈D1,D2,D3,D4〉,其中Di∈{D1,D3},若{NW,W,SW}∩ M(W,r(Di))=∅,则{NW,W,SW}∩Di+1=∅.
命题5 对于任一宽边界方向关系D=〈D1,D2,D3,D4〉,其中Di∈{D1,D3},若{NW,N,NE}∩ M(N,r(Di))=∅,则{NW,N,NE}∩Di+1=∅.
命题6 对于任一宽边界方向关系D=〈D1,D2,D3,D4〉,其中Di∈{D1,D3},若{SW,S,SE}∩ M(S,r(Di))=∅,则{SW,S,SE}∩Di+1=∅.
命题4~6成立,证明过程与命题3证明过程类似.
3 宽边界方向关系的相容性检测 3.1 定性空间约束满足问题在定性空间关系建模中,可将定性空间关系推理问题转换为定性空间约束满足问题(QS-CSPs,qualitative spatial constraint satisfaction problems). 1个 QS-CSPs通常抽象为值域 D 上的1组变量 V 和其上的1个约束集合 C ,因此形式化记为〈 V ,D ,C 〉. 目前,定性空间关系建模研究多基于平面空间. Allen利用路径相容算法(path-consistency)提出了一种区间对象间拓扑关系约束的相容性检测方法. 下面对Allen的方法进行扩展,研究不确定区域对象间方向关系约束的相容性检测问题.
3.2 宽边界方向关系约束定义10 Xu D Xv为1个宽边界方向关系约束,其中D=〈D1,D2,D3,D4〉为宽边界方向关系,Xu、 Xv为宽边界区域变量,Di∈ U ,1≤i≤4.
为方便说明,简记宽边界方向关系(BBDR,broad boundary direction relation)和基本主方向关系(BCDR,basic cardinal direction relation).
定义11 宽边界区域间方向关系的约束满足问题记为〈 V,D,C 〉BBDR,它是一类特殊的空间约束满足问题,其中 V 为一个有限变量集; D为V 中变量对应的值域,是2维平面空间中宽边界区域的无限集合; C 为宽边界方向关系约束集合. 若 C 是相容的,当且仅当存在对 V 的1组实例化X1=a1,…,Xn=an,其中ai为宽边界区域,ai以ai(2i-1)为内区域,ai(2i)为外区域,ai(2i-1),ai(2i)∈ R ,1≤i≤n,使得 C 是可满足的,称a1,…,an是 C 的1个解. C 的所有解的集合记为s( C ).
类似地,对于确定区域间基本主方向关系的约束满足问题,笔者形式化记为〈 V ,D ,C 〉BCDR.
约束转换规则1 对于宽边界方向关系约束满足问题中的任意一个变量Xi,1≤i≤n,对应2个确定区域变量x2i-1,x2i,使得x2i-1 B x2i成立.
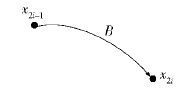
对于任意一个宽边界区域,其均由外、内2个确定的区域构成,若以外区域为参照区域,内区域为主区域,则内区域与外区域间满足基本主方向关系B. 如图 2(a)所示,宽边界区域a对应2个确定区域a1,a2,其中a2为a的外区域,a1为a的内区域,并有a1 B a2. 其对应的约束转换图如图 4所示.
约束转换规则2 对于任意一个宽边界方向关系约束Xi 〈D1,D2,D3,D4〉 Xj,宽边界区域变量Xi对应2个确定区域变量x2i-1,x2i,Xj对应2个确定区域变量x2j-1,x2j,使得x2i-1 D1 x2j-1,x2i-1 D2 x2j,x2i D3 x2j-1,x2i D4 x2j成立.
例3 宽边界方向关系约束Xi 〈NW,NW:N,NW:N,NW:N〉 Xj,执行约束转换规则2后得到1组确定区域间方向关系约束x2i-1 NW x2j-1,x2i-1 NW:N x2j,x2i NW:N x2j-1,x2i NW:N x2j.
转换后对应的约束转换图如图 5所示.
由约束转换规则1和2,可将1个〈 V,D,C 〉BBDR转换为1个〈 V,D,C 〉BCDR. 下面通过例4说明具体转换过程. 在此基础上,可通过扩展现有确定区域间方向关系的推理方法对不确定区域间方向关系进行推理.
例4 设宽边界方向关系约束集合
C ={X1 〈N,N,N:NE,N〉 X2,
X2 〈NW,NW,NW,N:NW〉 X3}
对宽边界方向关系约束X1 〈N,N,N:NE,N〉 X2中的2个宽边界区域变量X1、 X2分别执行约束转换规则1,得到
x1 B x2,x3 B x4
对宽边界方向关系约束X2 〈NW,NW,NW,N:NW〉 X3中的2个宽边界区域变量X1、 X2分别执行约束转换规则1,得到
x3 B x4,x5 B x6
对宽边界方向关系约束X1 〈N,N,N:NE,N〉 X2执行约束转换规则2,得到
x1 N x3,x1 N x4,x2 N:NE x3,x2 N x4
对宽边界方向关系约束X2 〈NW,NW,NW,N:NW〉 X3执行约束转换规则2,得到
x3 NW x5,x3 NW x6,x4 NW x5,x4 N:NW x6
对约束集合 C 进行转换后得到新的确定区域间方向关系约束集合 C ′和相应的变量集合 V ′.
V ′={x1,x2,x3,x4,x5,x6}
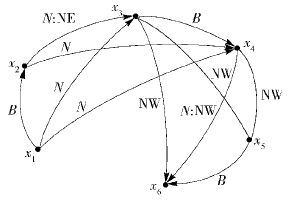
C ′={x1 B x2,x3 B x4,x5 B x6,x1 N x3,x1 N x4,
x2 N:NE x3,x2 N x4,x3 NW x5,x3 NW x6,
x4 NW x5,x4 N:NW x6}
对于一个宽边界方向关系约束满足问题〈 V,D,C 〉BBDR,判定其相容性的步骤如下.
步骤1 基于约束转换规则1,将宽边界区域变量集合 V 转换为确定区域变量集合 V ′,并将推导出的基本主方向关系约束放入 C ′中.
步骤2 基于约束转换规则2,将宽边界方向关系约束集合C转换为基本主方向关系约束集合C′.
步骤3 基于步骤1和步骤2,将〈 V,D,C 〉BBDR转换为〈 V′,D,C ′〉BCDR. 作为路径相容算法的关键技术,基本主方向关系间的相容性复合运算(记为“$\circ $”)已在很多文献中详细讨论[3,9]. 借助于这些运算性质,笔者给出针对〈 V,D,C 〉BCDR的路径相容性算法,从而间接实现对〈 V,D,C 〉BBDR相容性的判定.
算法具体描述如下.
宽边界方向关系相容性算法(BBDR-CON,consistency algorithm for BBDRs)
输入:〈 V,D,C 〉BBDR.
输出:s( C )非空输出“consistent”,否则输出“unconsistent”.
/*约束转换,V′,C ′分别表示执行约束转换后得到的确定区域变量集合和确定区域间方向关系约束集合*/
For all Xi in V o
V ′←{x2i-1,x2i}
C ′←{x2i-1 B x2i}
EndFor
For all Xi Dt Xj in C Do
C ′←{x2i-1 Dt1 x2j-1,x2i-1 Dt2 x2j,x2i Dt3 x2j-1,x2i Dt4 x2j}
EndFor
/*标记约束,u标记区域xu,Cuv标记xu,xv间的约束,1≤u,v≤2n*/
Q ←{〈u,v〉|u D v∈ C ′}
/*约束传播,T 为临时约束集合*/
While Q ≠∅ Do
Select and delete a 〈u,v〉 from Q
For all k (k≠u,k≠v,1≤k≤2n) Do
T ←Cuv∩(Cuk$\circ $ C kv)
If T =∅ Then return “unconsistent”
Else
If T ≠Cuv
Cuv← T
Add 〈u,v〉 to Q
EndIf
T ←∅
EndIf
EndFor
EndWhile
return“consistent”
BBDR-CON算法是正确的. 第一,Skiadopoulos等[3]证明了算法中复合运算的正确性;基于宽边界模型和主方向关系的形式化定义可知,算法中的约束转换规则是正确的. 第二,While循环是算法的主体部分,当约束集合 Q 不为空时,选择Cuv,然后选择与u,v能构成三角形的变量k,对边〈u,k〉,〈k,v〉标注的关系进行复合运算,并将Cuv与Cuk$\circ $ Ckv相交的结果存入临时约束集合 T 中. 若 T 为空,说明关系集合Cuv中没有属于关系集合Cuk$\circ $ Ckv的元素,这与路径相容的定义相冲突,则返回“unconsistent”;若 T 不为空,则用新约束集合 T 替换原有关系Cuv. 此时约束网络中的关系已被改动,重新将边〈u,v〉加入 Q 中,继续循环,直到当所有约束对应的边均被检测(即 Q 为空),若此时再无可能产生冲突的约束,则可判定约束集合是相容的.
BBDR-CON算法是对Allen的路径相容算法的扩展. 对于含有n个变量的宽边界方向关系约束满足问题,可转换为包含2n个变量的确定区域间方向关系的约束满足问题,对应于约束网络中的2n个结点,最多包含2n(2n-1)(2n-2)/6个三角形. 对这些三角形进行路径相容性检测所需的时间为O(n3),所以BBDR-CON算法的时间复杂度为O(n3).
4 结束语笔者采用定性方法,基于宽边界模型和基本主方向关系模型,研究了不确定区域间方向关系的表示和推理方法. 提出了宽边界区域间方向关系表示方法,并在此基础上提出一种基于宽边界方向关系约束的复杂度为O(n3)的相容性算法BBDR-CON. 与以往确定区域间方向关系模型相比较,笔者的工作能形式化表示和推理不确定区域间的空间关系,不仅进一步深化了空间关系建模理论研究,同时更有利于解决复杂实际问题.
理论研究方面,对于笔者提出的宽边界方向关系,其运算性质(逆运算、复合运算等)仍有待于深入研究. 现实世界中的空间对象更加复杂,导致不确定性的因素很多,不仅局限于带有不确定边界的区域对象,因此更接近人们空间认知的不确定空间对象的新表示方法是未来该领域中的一个研究热点. 应用研究方面,在城市交通、地理信息系统(GIS,geographic information system)、机器人导航和计算机辅助设计中,基于线性物体的方向关系推理也具有极高的应用价值,因此将笔者提出的方法应用于线性物体推理,是未来值得开展的一项应用研究工作.
| [1] | 谢琦, 刘大有, 虞强源, 等. 一种不确定区域间的方向关系模型[J]. 吉林大学学报:理学版, 2006, 44(5):748-753. Xie Qi, Liu Dayou, Yu Qiangyuan, et al. Direction relations model between indeterminate regions[J]. Journal of Jilin University:Science Edition, 2006, 44(5):748-753.[引用本文:1] |
| [2] | Chen Juan, Anthony G C, Liu Dayou, et al. A survey of qualitative spatial representations[J]. The Knowledge Engineering Review, 2013, 30(1):106-136.[引用本文:1] |
| [3] | Skiadopoulos S, Koubarakis M. Composing cardinal direction relations[J]. Artificial Intelligence, 2004, 152:143-171.[引用本文:9] |
| [4] | Skiadopoulos S, Koubarakis M. On the consistency of cardinal direction constraints[J]. Artificial Intelligence, 2005, 163(1):91-135.[引用本文:2] |
| [5] | Liu Weiming, Li Sanjiang. Reasoning about cardinal directions between extended objects:the NP-hardness result[J]. Artificial Intelligence, 2011, 175:2155-2169.[引用本文:1] |
| [6] | Mossakowski T, Moratz R. Qualitative reasoning about relative direction of oriented points[J]. Artificial Intelligence, 2012:34-45.[引用本文:1] |
| [7] | Cierone S, Felice P D.Cardinal relations between regions with a broad boundary[C]// The 8th ACM Symposium on Advances in Geographic Information Systems(GIS'00), 2000:15-20.[引用本文:2] |