2. 北方工业大学 经济管理学院, 北京 100143
提出了一种双有限异质社交网络结构,即网络规模有限性、节点出/入度有限性以及网络节点属性的异质性.仿真结果及实证分析表明,与小世界网络、无标度网络等相比,双有限异质社交网络模型可以更好地模拟实际社交网络,不仅其网络整体结构兼具小世界特性和无标度特性,在微观上还可以真实反映出不同属性类型的节点在网络中的影响力和控制力.
2. School of Economics and Management, North China University of Technology, Beijing 100143, China
A double limited and heterogeneous social network was proposed to analyze the structure of social network in China, namely the limited size of the network and in-degree and out-degree of the nodes, and the heterogeneous attributes of the nodes. Compared with the small-world and scale-free network, the double limited and heterogeneous social network can better simulates the real social network. It not only has the overall structure characteristics of the small-world and scale-free network, but also reflects the influence and control of the different types of nodes in the social network at the micro level.
社交网络已渗透到工作、生活的方方面面,成为人们信息发布、获取、分享的重要平台,对其网络结构性质的研究具有重要的意义[1].已有研究积累了丰富的成果[2-5],但也存在有待进一步研究的问题.本研究在分析社交网络演化特征的基础上,以新浪微博为例,通过大规模数据分析,提取相关网络演化参数,并基于Netlogo软件模拟了新浪微博网络的动态演化过程,从而提出了双有限异质社交网络模型.
1 双有限异质社交网络建模本研究在已有社交网络经验模型的基础上,将双有限异质性补充到社交网络演化机制中,进而得到社交网络演化的4个基本规则.
规则一:单位时间内新增用户数与已有网络规模和潜在用户规模相关;新增节点所属类型依概率决定.
规则二:新增节点出度有限,其连接符合局域偏好连接特性[6],以及用户类型选择偏好特性,即出度异质性.
规则三:已有节点允许增加新边,新的连接可按照3种方式产生,即依概率与其他节点随机连接[7],基于三角推荐机制与关注的关注节点相连[8],基于互粉规则与已有粉丝相连.
规则四:已有节点允许退出网络,或断开旧的连接.
基于双有限异质社交网络演化的4个基本规则,其演化进程可描述如下.
第1步 初始网络设定.
初始社交网络由k类不同属性的M0个节点组成,并构成共N0条边的全耦合网络:
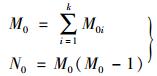
|
(1) |
第2步 网络演化.
在每一个时间步长,循环执行以下步骤,直至网络节点总数达到M.
1) 新增节点
t时刻新增节点数ΔM(t)依概率pch_i(i=1, 2, …, k)选择属性,且满足
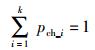
|
(2) |
确定新增节点连接数.新增节点new_j根据所属类型的出度分布特征,依概率plink_out_i(i=1, 2, …, k)确定出度nlink_out_i_new_j.
确定各新增节点的新增连接中与各类属性节点连接数量.新增节点new_j与第i类属性节点连接数量knew_j_link_i为
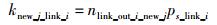
|
(3) |
其中:nlink_out_i_new_j为新增节点new_j的类型;ps_link_i为第s类节点与第i类节点连接的概率,且满足
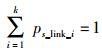
|
(4) |
明确新增节点选择关注对象的范围.新增节点可在所处位置半径r0范围内的局域网络Ω内选择关注对象.局域网络中除新增节点外第i类属性用户构成备选集Γi(i=1, 2, …, k).
确定新增节点关注对象.新增节点new_j在第i类属性备选集中参考无标度网络连接规则,依概率pnew_j_i_h选择关注对象,且pnew_j_i_h满足
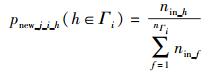
|
(5) |
其中:nin_h为第h个节点的入度,nΓi为备选集Γi中节点的个数.
2) 已有节点新增连边
选择已有节点.依概率pold_i随机选择nold个已有节点.
参考纽曼-瓦茨(NW, Newman-Watts)小世界网络连接规则,依概率pold_link_NW为已有节点nold_i随机选择一个已有节点old_j,并建立一条已有节点nold_i到已有节点nold_j的连接.
参考HK(Holme & Kim)可调簇系数模型的连接规则,依概率pold_link_hk为已有节点nold_i随机选择一个已有节点old_f,并确定节点old_f的关注集Φold_f.在关注集Φold_f中依概率pold_i_f_h选择关注对象,且满足
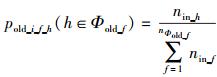
|
(6) |
其中nΦold_f为关注集Φold_f中节点的个数.
确定互粉对象.确定新增节点new_j的关注集Φnew_j,根据新增节点new_j所属类型i的互粉特征确定互粉比例phf_i,依概率pi_hf_h确定互粉节点,且pi_hf_h满足
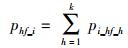
|
(7) |
3) 已有节点删除及已有边断开
选择删除节点.依概率pdelete_node随机选择ndelete_old个已有节点并删除.
选择断开边.依概率pdelete_link随机选择ndelete_link条已有边并删除.
2 仿真结果利用多主体仿真平台Netlogo,以新浪微博实证分析结果作为模型参数,模拟双有限异质社交网络.仿真结果表明,基于双有限异质社交网络演化规则构建的社交网络,平均最短路径较小、平均聚集系数较高,且入度服从幂率分布,兼具有小世界特性及无标度特性;此外,不同属性的各类节点对网络的影响力和控制力不尽相同.
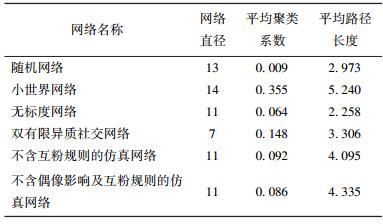
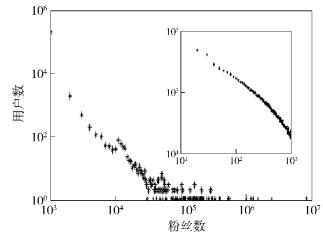
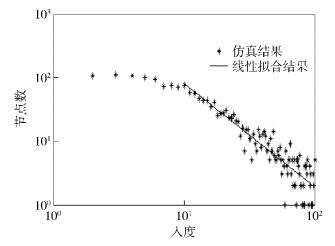
2.1 整体网络分析将仿真时长设定为289 s,得到由2 025个节点、38 108条边构成的双有限异质社交网络,将其与节点总数相同且总边数接近的随机网络、小世界网络、无标度网络比较,如表 1所示.仿真结果表明,双有限异质社交网络具有小世界特征,但出度分布服从给定分布(如图 1所示),入度分布服从幂率分布(如图 2所示),并具有无标度特征,但其聚集系数较大(如表 2所示),符合实际社交网络特征.
|
|
表 1 各类网络比较 |
|
图 1 新浪微博用户出度分布 |
|
图 2 仿真结果入度分布 |
|
|
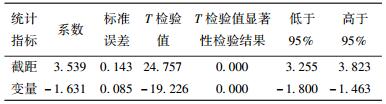
表 2 仿真结果入度双对数分布参数 |
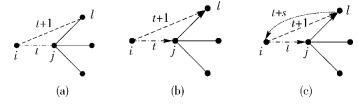
双有限异质社交网络聚集系数的增加与2类规则相关:① TF连接规则;② 互粉规则. TF规则可描述为若节点i和节点j在演化过程中t时刻已经建立了连接,则在t+1时刻,从节点j的邻居节点中选择一个节点l与节点i进行连接.在无向网络中,TF规则使节点i、j、l构成了封闭三角形,如图 3(a)所示,从而提升了网络聚集系数.但若真实社交网络是一个有向图(如微博),节点i、j、l并未构成封闭三角形,如图 3(b)所示,因而网络的聚集系数并未因TF规则而显著增加,如表 2所示.在TF规则的基础上增加互粉规则,通过建立节点l到节点i的连接,如图 3(c)所示,可以真正形成节点i、j、l之间的封闭三角形,有效提升社交网络的聚集系数.
|
图 3 网络节点连接示意图 |
1) 点度中心度
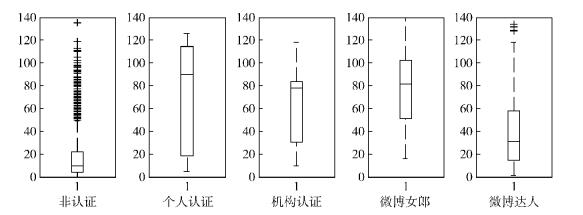
在社交网络中,可用节点的入度表示点度中心度.一个节点的中心度越高,表示与该节点的连接越多,节点影响力越大.在仿真得到的双有限异质社交网络中,各类属性节点的平均点度中心度不尽相同,如图 4所示.
|
图 4 各类属性节点点度中心度箱图 |
5类用户中,非认证用户和微博达人点度中心度平均值相对较低,但有少数用户具有较高的点度中心度,影响力较大;个人认证用户、机构认证用户及微博女郎点度中心度平均值较高,其中微博女郎点度中心度分布较为均匀,是值得重点关注的一类用户.
2) 中介中心度
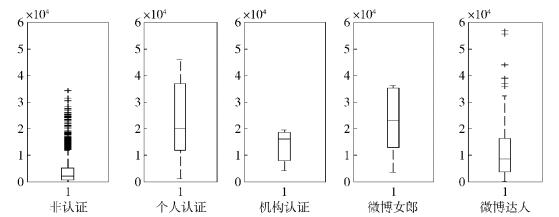
如果一个节点处于所有节点对的n条捷径上,n越大,则该节点在网络中的地位越重要.中介中心度可以表征节点对信息的控制程度.在仿真得到的双有限异质社交网络中,各类属性节点的中介中心度不尽相同,如图 5所示.
|
图 5 各类属性节点中介中心度箱图 |
5类用户中,非认证用户和微博达人中介中心度平均值相对较低,但有少数用户具有较高的中介中心度,对信息扩散具有较大的控制权;个人认证用户、机构认证用户及微博女郎中介中心度平均值较高,对信息扩散的平均控制力较强.
3 结束语社交网络结构决定了社交网络中信息传播的模式和效果,是开展社交网络相关研究的基础.在已有研究的基础上,本研究深入探讨了社交网络各类属性节点微观行为特征及其所形成的宏观演化规律,并以新浪微博实证分析结果作为模型参数,利用Netlogo平台进行了基于多Agent的仿真分析,得到以下2点结论.
第一,社交网络具有双有限异质特征,即网络规模有限性、节点出/入度有限性以及单模网络节点属性具有异质性.
第二,双有限异质社交网络模型可以更好地模拟实际社交网络.从宏观角度出发,双有限异质社交网络整体结构兼具小世界特性和无标度特性,但不能仅由小世界网络或无标度网络代替;从微观角度出发,它可以真实反映出不同属性类型的节点在网络中的影响力和控制力.
| [1] | Du S Y, Qi J Y. Research on influence of online social network structure on information dissemination-taking one laboratory of BUPT as an example[J].Journal of Beijing University of Posts and Telecommunications (Social Sciences Edition), 2013(6): 1–7. |
| [2] | Wang C C, Chen C, Dong Z Q. Effect of network structure on rumor propagation[J].Journal of System Simulation, 2013(1): 127–131. |
| [3] | Kwak H, Lee C, Park H, et al. What is Twitter, a social network or a news media[C]//Proceedings of the 19th International Conference on World Wide Web.[S. l. ]: ACM, 2010: 591-600. |
| [4] | Mislove A, Marcon M, Gummadi K P, et al. Measurement and analysis of online social networks[C]//Proceedings of the 7th ACM SIGCOMM Conference on Internet Measurement.[S. l. ]: ACM, 2007: 29-42. |
| [5] | Saino L, Cocora C, Pavlou G. A toolchain for simplifying network simulation setup[C]//Proceedings of the 6th International ICST Conference on Simulation Tools and Techniques. NewYork: SIMUTOOLS, 2013: 82-91. |
| [6] | Guo H, Bu Y J, Lan J L. Novel dynamic evolution model for Internet AS-level topology[J].Journal of Systems Engineering, 2011(2): 152–159. |
| [7] | Yang X C, Sui Y, Yue X. Social relationship network construction on organization Microblog-a case study of Tencent business school[J].Journal of Beijing University of Posts and Telecommunications(Social Sciences Edition), 2012(3): 21–27. |
| [8] | Ma F C, Liu X. Evolvement model for scientific knowledge networks[J].Systems Engineering-Theory & Practice, 2013(2): 437–443. |