2. 中国科学院大学, 北京 100049;
3. 北京邮电大学 网络与交换技术国家重点实验室, 北京 100876
智能电网在给人们带来巨大的效益的同时, 也会产生严重的安全问题.其中, 针对实时电价(RTP)的网络攻击值得重视, 但是人们关注较少.针对时延攻击, 为电力市场中用户与供应商的行为建立了动态模型, 并在此基础上, 利用鲁棒控制理论和李雅普诺夫函数法, 提出了一种抵御时延攻击的电价策略.最后, 通过一个数值示例验证了该策略的有效性.
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. State Key Laboratory of Networking and Switching Technology, Beijing University of Posts and Telecommunications, Beijing 100876, China
The smart grid does provide people with enormous benefits, however, but it possibly leads to serious security problems. The cyber attack on real-time pricing (RTP) is of great significance, but people pay less attention to. Focused on delay attack, a dynamic model for behavior of both consumers and suppliers in electrical power markets was established. Based on the model, a defensive pricing strategy using robust control theory and Lyapunov function was put forward. At last, the effectiveness of the proposed strategy was validated through a numerical simulation example.
智能电网(Smart Grid)是一种现代化的电力网络,它采用模拟或数字的通信技术,对信息(如电力提供商和用户的行为)加以收集、利用,以一种自动化的方式来提升发电配电的效率、可靠性、经济效益和可持续性[1].学界近年来对智能电网安全进行了广泛而深入的研究[2-3].但这些研究却很少针对实时电价的时延攻击问题.
利用鲁棒控制理论和李雅普诺夫函数方法,提出了一种新的实时电价策略,确保在存在有界随机时延的情况下,实时电价系统仍然能够维持电力市场供需平衡.数值仿真实验验证了该实时电价策略的有效性.
1 实时电价模型1.1 实时电价的反馈作用在电力市场中,由于人的逐利性,电力用户和供应商都会根据实时电价的高低来调整自身的消费和生产行为.对于二者的动态模型,已有文献都进行过深入的研究[4].在本研究中,从控制理论的角度出发,用离散线性时不变模型对其加以描述.
1.2 实时电价的反馈作用从用户的角度,记xd(k)∈ℝn为n个(组)用户在时刻k的实际用电需求,yd(k)∈ℝm为m个电力供应商在时刻k需要为用户生产的电能,ur(k)∈ℝ为时刻k发布的实时电价.那么,在实时电价的调控下,用户用电需求的动态模型可以用如下的离散线性系统来描述:
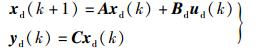
|
(1) |
其中:A∈ℝn×n描述用户当前时刻的用电需求与以往时刻(上一时刻)的关系;Bd∈ℝn×1描述用户需求与实时电价之间的关系;C∈ℝm×n描述电力提供商对于用户需求的分担关系;ud(k)=ur(k)-ud*是用户对实时电价的反应;ud*∈ℝ是对用户而言的稳定电价,即在这一电价下,用户对于电价的反应为零. A,Bd,C是已知矩阵,ud*是已知常量.假设电力供应商提供的电能总是能够满足用户的需求.
1.3 供应商模型从供应商的角度,记ys(k)∈ℝm为m个电力供应商在时刻k计划生产的电能.相应地,可以认为存在一个虚拟的关于供应商的动力学模型如式(2) 所示.该模型具有与用户模型相似的形式:
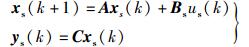
|
(2) |
其中:xs(k)∈ℝn为n个(组)用户在时刻k的计划用电量;us(k)=ur(k)-us*是供应商对实时电价的反应;us*∈ℝ是对供应商而言的稳定电价,即在这一电价下,供应商对于电价的反应为零. Bs∈ℝn×1是已知矩阵,us*是已知常量.假设u*=ud*=us*,因为市场中,供需双方任何一方对于实时电价的单方面反应,都会导致供求关系偏离平衡,使实时电价失稳.记u(k)=ur(k)-u*,则式(1),式(2) 可以改写为:
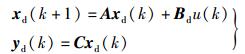
|
(3) |
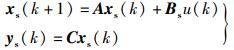
|
(4) |
从前面的分析可以看到,要使电力市场供需平衡,即要使yd(k)=ys(k),等同于使xd(k)=xs(k).记误差e(k)=xs(k)-xd(k),矩阵B=Bs-Bd,则由式(1),式(2) 可得如下的误差离散动态系统:
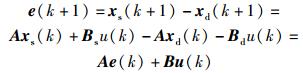
|
(5) |
定义1[5] 考虑具有唯一平衡点z=0的离散系统z(t+1)=f(z(t), t),如果对于任意正实数ε及任意非负整数t0,存在δ(ε, t0)>0,使得当初始状态‖z0‖ < δ(ε, t0)时,有‖z(t, t0, z0)‖ < ε对所有t≥t0成立,且有
取电价控制策略为
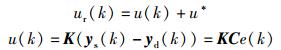
|
(6) |
将式(6) 代入式(5),可得无时延时的误差模型:
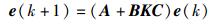
|
(7) |
可见,在无时延攻击的情况下,使误差系统式(7) 渐近稳定的关键在于:求解合适的控制增益矩阵K,使矩阵A+BKC的特征根位于单位圆内.
2 抗时延攻击的实时电价策略2.1 问题描述由电力市场误差模型(5),以及实时电价策略式(6) 可知,当k时刻的电价信号存在离散随机时延τ(k)时,误差模型可写为:
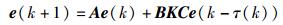
|
(8) |
其中τ(k)∈{1, 2, …, d},正整数d为时延的上限.本节的重点在于求取合适的控制增益K,使得带时延τ(k)的误差系统式(8) 渐近稳定.
2.2 抗时延攻击的电价策略基于前面的建模和分析,将给出求取控制增益矩阵K,以保证误差系统式(8) 渐近稳定的方法.
定理1 对于给定的最大时延d,如果存在反馈控制增益K和合适维数的矩阵P=PT>0,Q=QT≥0,Z=ZT≥0,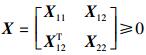
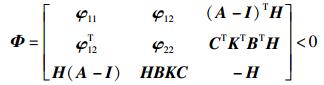
|
(9) |
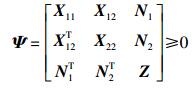
|
(10) |
其中:
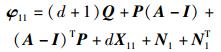
|
(11) |
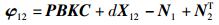
|
(12) |
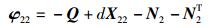
|
(13) |
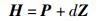
|
(14) |
其中I为单位矩阵.
证明:设η(l)=e(l+1)-e(l),可以得到:
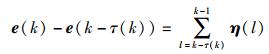
|
(15) |
选取如下的Lyapunov函数:
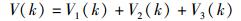
|
(16) |
其中,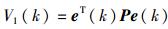
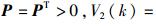
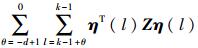
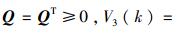

定义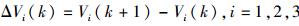
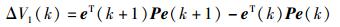
|
(17) |
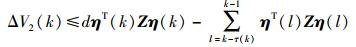
|
(18) |
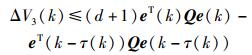
|
(19) |
引入自由权矩阵N1和N2,由式(15) 可得:
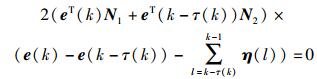
|
(20) |
对任意维数合适的矩阵
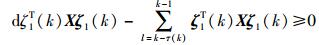
|
(21) |
其中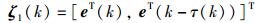
定义ΔV(k)=V(k+1)-V(k),则将式(20),式(21) 的左边加入到ΔV(k)中可得:

|
(22) |
其中
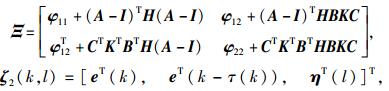
|
Ψ由式(10) 给出,φ11,φ12,φ22,H由式(11)~(14) 给出.利用Schur补定理[6],Ξ < 0等价于Φ < 0.从式(22) 可以看到,如果Ξ < 0,Ψ≥0,则误差系统式(8) 渐近稳定,定理得证.
由于式(9) 中含有PBKC等非线性项,所以定理1中的反馈控制增益K不能直接用线性矩阵不等式(LMI,linear matrix inequality)求解,因此还需要作进一步的讨论.
2.3 控制器设计本节将进一步讨论如何求解控制增益矩阵K.
定理2 对于给定最大时延d,如果存在L=LT>0,W=WT≥0,R=RT≥0,
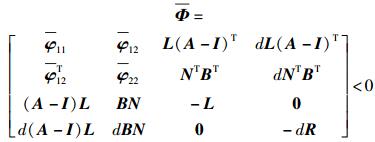
|
(23) |

|
(24) |
其中
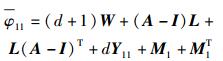
|
(25) |
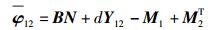
|
(26) |
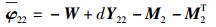
|
(27) |
则误差系统式(8) 渐近稳定.
篇幅所限,证明从略.
定理2的条件中只有式(24) 含有非线性项LR-1L,因此可借助锥补线性化[7]将上述问题转化为非线性最小化问题,利用MATLAB的LMI工具箱迭代求取次优解.定理2中对应的控制增益矩阵为K=N(CL)l-1,(CL)l-1为CL的左逆矩阵.只要取这样的K作控制增益矩阵,按式(6) 制定实时电价,就可确保电力市场在遭受有界随机时延攻击时,仍然保持供需平衡.
3 数值仿真本节进行了一个数值仿真实验,用以验证提出的实时电价策略对于时延攻击的防御作用.
考虑具有2组用户和2个供应商的电力市场模型(单位为万千瓦),其中各矩阵取值如下:
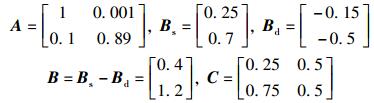
|
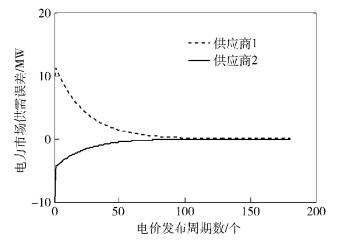
假设电力市场存在初始供求误差[1 -1]T.当不存在时延攻击时,由误差系统模型式(8) 可得控制增益K=[-1.268 8 -0.068 7].此时,电力市场供需误差如图 1所示.从图中可见,在无时延攻击时,原有的实时电价策略可以使电力市场供需趋于平衡.
|
图 1 未受时延攻击时电力市场的供需误差 |
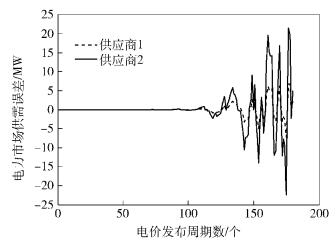
当存在随机时延τ(k)∈{1, 2, …, 10}时,如果沿用上述控制增益,那么,电力市场供需误差将如图 2所示.从图中可见,在受到有界随机时延攻击时,原有的电价策略已无法平衡电力市场的供需关系.
|
图 2 受到时延攻击时电力市场的供需误差 |
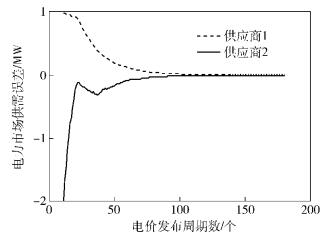
如果采用提出的新的控制算法,可以得到新的控制增益矩阵K=[0.288 2 -0.488 6].此时,电力市场供需误差将如图 3所示.从图中可见,提出的实时电价策略,对于有界随机时延攻击,具有抵御作用.
|
图 3 利用提出的电价策略时的电力市场供需误差 |
为实时电价调控下的电力市场建立了动态模型,并在模型基础上,提出了新的实时电价策略,确保在遭受有界时延攻击的情况下,电力市场的供给与需求仍然能够趋于平衡.
| [1] | United States Department of Energy. "Grid 2030"—a national vision for electricity's second 100 years[EB/OL]. Washington: United States Department of Energy, 2003[2015-02-09]. http://energy.gov/sites/prod/files/oeprod/DocumentsandMedia/Electric_Vision_Document.pdf. |
| [2] | Liu Yao, Ning Peng, Reiter M K. False data injection attacks against state estimation in electric power grids[C]//Proceedings of the 16th ACM Conference on Computer and Communications Security. NewYork: ACM Press, 2009: 21-32. |
| [3] | Grochocki D, Huh J H, Berthier R, et al. AMI threats, intrusion detection requirements and deployment recommendations[C]//Proceedings of 2012 IEEE Third International Conference on Smart Grid Communications. Tainan: IEEE, 2012: 395-400. |
| [4] | Roozbehani M, Dahleh M A, Mitter S K. Volatility of power grids under real-time pricing[J].IEEE Transactions on Power Systems, 2012, 27(4): 1926–1940. doi: 10.1109/TPWRS.2012.2195037 |
| [5] | Ogata K. Discrete-time control systems[M]. Englewood Cliffs: Prentice Hall, 1994. |
| [6] | Boyd S, Ghaoul L E, Feron E, et al. Linear matrix inequalities in system and control theory[M]. Philadelphia: Society for Industrial and Applied Mathematics (SIAM), 1994. |
| [7] | Moon Y S, Park P, Kwon W H, et al. Delay-dependent robust stabilization of uncertain state-delayed systems[J].International Journal of Control, 2001, 74(14): 1447–1455. doi: 10.1080/00207170110067116 |


