2. 江苏省无线传感网高技术研究重点实验室, 南京 210003;
3. 北京邮电大学 网络与交换技术国家重点实验室, 北京 100876
网络流量预测是网络管理的重要内容, 高效的流量预测方法可提高网络管理效率.针对网络流量的时变性等问题, 提出了一种基于智能优化的分布式网络流量预测方法.该方法采用果蝇算法优化3次指数平滑预测模型中的平滑因子, 对时间窗口内收集到的网络流量进行预测, 从而有效地提高3次指数平滑模型下网络流量预测的准确度与效率.仿真实验表明:相比传统3次指数平滑预测模型, 此方法可解决平滑因子的不确定性所导致的预测结果误差问题, 有效提高了网络流量预测精度.
2. Jiangsu High Technology Research Key Laboratory for Wireless Sensor Networks, Nanjing 210003, China;
3. State Key Laboratory of Networking and Switching Technology, Beijing University of Posts and Telecommunications, Beijing 100876, China
Efficient network traffic prediction method can improve the efficiency of network management. On account of problems of network traffic if as burst, time-varying, nonlinear problems happen that caused by various coefficients, a distributed network traffic prediction method was proposed obeyed by intelligent optimization. The fruit fly optimization algorithm was adopted in this method to optimize the smoothing coefficients of traditional triple exponential smoothing forecasting model. By predicting network traffic that is collected within time windows, this method effectively improves the efficiency of network traffic prediction. Simulation indicates that, compared with traditional triple exponential smoothing forecasting model, the proposed prediction model can solve the problem of prediction error caused by smoothing coefficient. The optimal smoothing coefficient can be selected adaptively, thus improves the prediction accuracy.
高效的网络流量模型与流量预测方法是网络性能分析和网络规划的基础,其对网络管理、网络故障等具有重要意义.如何有效建立网络流量模型并进行流量预测引起了研究者的广泛关注.现有的典型工作包括:自回归(AR,autoregressive)模型[1]、自回归滑动平均(ARMA,autoregressive and moving average)模型[2]及自回归积分移动平均(ARIMA,autoregressive integrated moving average)模型[3]等,这些线性预测模型具有易于实时更新数据、大规模应用等优点.共同的问题:这些模型难以同时对平稳或非平稳的网络流量数据进行准确预测.事实上,实际网络流量数据受限于诸多因素,预测模型需要适应各种流量. 3次指数平滑模型[4]作为一种适应各种观测数据的预测方法,能预测非线性趋势的序列,其目标是使预测值和实测值间的均方差(MSE)最小. 3次指数平滑的预测值既能反映最新的观测数据,又能保留历史信息,使得预测结果更符合实际情况,平滑系数的取值将很大程度上影响预测准确性.目前,一般通过经验判断及序列走向大致确定系数取值范围.近年来,一些预测模型尝试采用启发式算法对参数预测,包括蚁群算法[5]等,但算法相对复杂.果蝇优化算法(FOA,fruit fly optimization algorithm)[6]是近年来提出的一种新型进化优化方法,具有简单、快速收敛等优点.
针对分布式网络环境,基于3次指数平滑模型,研究并设计了基于智能优化的流量预测方法,该方法采用果蝇算法采用预测的均方误差(MSE)为目标函数以优化预测模型中的平滑指数.算法充分借鉴了果蝇优化算法收敛速度快及3次指数预测模型性能高等优点,最终实现网络流量的高效预测.
1 相关工作1.1 果蝇优化理论[6]FOA是近年来提出的寻求全局优化的新方法,由果蝇觅食行为推演出.由于果蝇具有嗅觉器官非常发达的特点,它在飞行中能通过空气中的气味感知食物源的方向,在飞至距离食物较近位置后能够使用敏锐的视觉发现食物以及同伴聚集的位置,再飞往该方向,最后找到食物.该算法具有收敛速度快、稳定等优点.其基本原理如下.
对果蝇群体位置进行随机初始化;给出果蝇个体搜寻食物的随机方向与距离;由于无法得知食物位置,因此先估计与原点之间的距离,再计算味道浓度判定值;味道浓度判定值代入味道浓度判定函数以求出该果蝇个体位置的味道浓度;找出此果蝇群体中味道浓度最高的果蝇;保留最佳味道浓度值与x、y的坐标,此时果蝇群体利用视觉往该位置飞去;进入迭代寻优,重复执行,并判断味道浓度是否优于前一迭代味道浓度,若是,则保留该值,继续迭代直到终止条件满足.综上,果蝇优化算法具有操作简单、收敛速度快等优点.
1.2 3次指数平滑预测模型[4]网络流量具有较强的突发性,需要建立高效的网络流量预测模型,才能较为准确地预测网络流量.时间序列预测法是一种对历史信息的预测,根据时间数列所能反映的变量发展过程和规律性,预测其发展趋势的方法. 3次指数平滑法是时间序列预测中的一种预测方法,也可以进行中期和短期预测. 3次指数平滑法的基本途径是对2次指数平滑再进行1次指数平滑来分析预测的一种方法.当观测数据呈现非线性走向时,可采用3次指数平滑法进行预测分析,对观测数据进行3次指数平滑后,估计2次多项式参数,建立预测模型.
设观测数据序列为y1, y2, …, yt,使用字母S表示指数平滑值,第t时间段第i次指数平滑值记为St(i),St-1(i)为St(i)前一时间段的第i次指数平滑值,各时间段指数平滑值的计算如下:
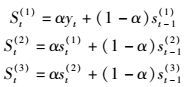
|
(1) |
其中:yt是第t时间段的实际值,α是指数模型中的平滑系数(0<α<1),3次指数平滑法的数学模型为:
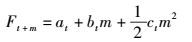
|
(2) |
其中:m为预测时间段数,at、bt、ct为预测参数. at、bt、ct的计算式为

|
(3) |
3次指数平滑实质上是一个迭代计算的过程,它的初始值由观测数据序列之前的所有数值的加权平均值.预测过程中平滑系数α的合理取值对预测的精度有重要影响. α可以认为是新旧数据的一个分配比例,当α越大时,新的观测数据占的比较越大.当观测数据长期趋势比较稳定,α适宜取小值,当观测数据波动幅度比较大时,α适宜取大值,能较好地跟踪新数据的变化.根据实际情况选择合理的平滑系数,才能取得较为准确的预测结果.
2 基于智能优化的流量预测模型基于3次指数平滑的流量预测模型中平滑指数对预测效果具有相当大的影响,通常使用该方法预测时,平滑指数的选取是通过经验判断或者序列走向大致确定范围,很难取得最优的平滑指数,导致预测结果存在较大误差.因此,采用果蝇优化算法优化平滑指数,通过不断地寻优得到预测效果最优的3次指数平滑模型的平滑指数,解决3次指数预测模型中由于平滑指数的选择造成预测结果不同程度上预测误差的问题.采用果蝇优化算法优化基于3次指数平滑的预测模型中的平滑指数,优化过程中通过不断迭代寻优得到效果最佳的平滑指数,最终得到误差最小的预测结果.采用FOA优化的3次指数平滑预测模型的具体步骤如下:
步骤1 设置分布式网络环境参数:分布式网络可控流量中心数量及各流量中心产生的流量(Mbit/s);
步骤2 网络环境中各流量中心进行流量采集;
步骤3 分布式网络每个网络流量中心收集到的网络流量采用基于智能优化的分布式网络流量预测方法进行流量预测;
步骤4 设置优化算法中果蝇种群个体数量(sizepop)及最大迭代次数(max gen),随机生成果蝇种群的初始位置(IntX_axis, IntY_axis),为种群的中心位置;
步骤5 给出果蝇种群中个体搜索食物的飞行方向和飞离位置中心的距离,方向和距离随机生成(Xi, Yi);
步骤6 估计个体果蝇位置与原点之间的距离Disti,并由此计算味道浓度判定值Si=1/Disti.然后,将Si代入3次指数平滑预测模型中,在该模型中,其平滑指数α表示为Si.根据预测模型的结果,得到它的Smelli,也即味道浓度判定函数(fitness function),Smelli表示为均方误差MSE来测量预测结果和实际值之间的偏差:
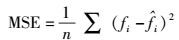
|
(4) |
其中:n是预测阶段总数,fi是阶段i的实际值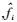
步骤7 找出此果蝇种群个体中Smelli最小的果蝇;记录最佳味道浓度值(Si)与(Xi,Yi)坐标,此时果蝇群体向该位置飞去;
步骤8 迭代寻优,重复果蝇优化过程,并找出优于前一迭代的味道浓度坐标值,直到迭代结束.
3 实验及分析为验证设计方法的有效性,进行了仿真验证.针对分布式网络下的各子网络采用时间窗机制采集流量,为方便后面的数据处理,首先对流量数据归一化处理,在此基础上采用提出的方法进行流量预测.通过FOA优化的3次指数平滑模型对网络流量进行预测,设定迭代次数Maxgen=25,种群规模sizepop=20. 图 1是经果蝇优化算法25次迭代寻优后得到最佳的平滑指数为α=0.352 7时的预测结果.

|
图 1 基于智能优化的3次指数平滑预测结果 |
进一步,将设计的基于FOA优化的3次指数平滑流量预测与基于粒子群(PSO, particle swarm optimization)优化方法进行比较,重复实验15次后将平均收敛情况对比,如图 2所示.将FOA优化过程重复15次之后,经FOA算法的25次迭代动态调整平滑指数后的均方误差(MSE),平均经过4代收敛,误差MSE为0.043 75;PSO算法在19代时实现了收敛,FOA收敛速度优于PSO算法.

|
图 2 2种方法平均收敛情况对比 |
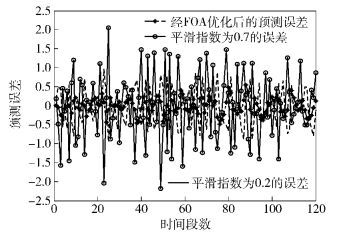
为进一步验证采用FOA算法优化后模型预测的准确性,采用原始的3次指数平滑预测对数据进行预测,与优化后的预测数据进行对比.由于平滑指数α的取值存在不确定性,人为根据经验判断或者序列走向大致确定额定的范围取值,这里将平滑指数选为α=0.2与α=0.7进行预测,图 3是3次预测后均方误差MSE的比较.
|
图 3 基于智能优化的3次指数平滑预测误差 |
图 3对FOA优化的3次指数平滑预测误差及3次指数平滑预测误差进行分析对比,可以发现,通过智能优化平滑参数后,预测效果明显提高,优化后的预测误差相对于原始的3次指数平滑预测的误差显著减小.
进一步分析,选取均方误差(MSE)、平均绝对百分比误差(MAPE)和平均绝对误差(AAE)用来评估不同预测方法的结果,MSE、MAPE和AAE的值根据下式计算:
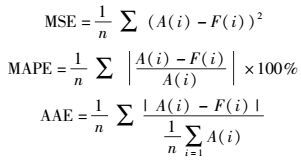
|
其中A (i)是初始网络流量值,F (i)是预测流量值.
通过表 1对比发现,经过FOA优化的3次指数
|
|
表 1 流量预测精度 |
平滑预测的MSE、MAPE和AAE误差大幅度小于原始的3次指数平滑预测误差,预测精度更高.
4 结束语提出了基于智能优化的预测模型对网络流量进行预测,利用果蝇优化算法优化3次指数平滑预测模型中的平滑指数,对网络流量进行准确预测.仿真结果表明:经果蝇优化算法优化平滑指数后的3次指数平滑预测模型,可针对网络流量序列选择最优平滑指数,解决了平滑指数的不确定性导致的预测误差,有效提高了网络流量的预测精度.
| [1] | Nakajima J, Kasuya M, Watanabe T. Bayesian analysis of time-varying parameter vector autoregressive model for the Japanese economy and monetary policy[J].Journal of the Japanese and International Economies, 2011, 25(3): 225–245. doi: 10.1016/j.jjie.2011.07.004 |
| [2] | Sun Y, Wang R, Sun B, et al. Prediction about time series based on updated prediction ARMA model[C]//FSKD 2013. Shenyang: IEEE Press, 2013: 680-684. |
| [3] | Sang Aimin, Li Sanqi. A predictability analysis of network traffic[C]//INFOCOM 2000. Israel: IEEE Press, 2000: 342-351. |
| [4] | Kuang J, Zhai D, Wu X, et al. A network traffic prediction method using two-dimensional correlation and single exponential smoothing[C]//ICCT 2013. Guilin: IEEE Press, 2013: 403-406. |
| [5] | Liao R J, Zheng H B, Grzybowski S, et al. Fuzzy information granulated particle swarm optimization-support vector machine regression for the trend forecasting of dissolved gases in oil-filled transformers[J].IET Electric Power Applications, 2011, 5(2): 230–237. doi: 10.1049/iet-epa.2010.0103 |
| [6] | Pan W T. A new fruit fly optimization algorithm: taking the financial distress model as an example[J].Knowledge Based Systems, 2012, 26: 69–74. doi: 10.1016/j.knosys.2011.07.001 |



