2. 北京邮电大学 网络与交换技术国家重点实验室, 北京 100876
在智能电网中, 与传统路由协议不同, 突发性拥塞不再是数据采集的主要风险, 风险的新来源是数据流过度集中在网络的关键节点而导致的拥塞.为此, 提出了一种能够实现数据平衡的数据采集路由机制用以克服网络拥塞.首先, 该机制抽象出配用通信网络的数学模型; 其次, 针对无线网状网络(WMNs)路由协议, 以节点排队队列长度作为决策参数建立路由度量模型(数据平衡度量模型, DBMM), 并以度量值最小作为决策条件, 设计了基于平衡树的路由算法(基于DBMM的路由算法, RA-DBMM).最后, 在Matlab环境下进行仿真实验, 对比分析RA-DBMM和经典Bellman-Ford的性能差异.实验结果表明:RA-DBMM能够有效地改善数据拥塞问题, 提高系统可靠性和吞吐量.
2. State Key Laboratory of Networking and Switching Technology, Beijing University of Posts and Telecommunications, Beijing 100876, China
Different from traditional routing protocols in smart grid, the sudden congestion is no longer as main risk for data collection. The source of risk is currently key node congestion in network. A routing mechanism was proposed to realize reliable data acquisition of electric data transmission for load balance of network congestion. Firstly, an abstract mathematical model of communication network was built. Secondly, the routing protocol for wireless mesh networks (WMNs) was used. The node queue length was regarded as the decision parameters to establish a routing metric model (Data Balance Measurement Model, DBMM) corresponding to the routing algorithm based on the balanced tree (Routing Algorithm based on DBMM, RA-DBMM). Simulation was carried out in MATLAB environment, the performance was compared between the RA-DBMM algorithm and the classical Bellman-Ford algorithm. Experiments show that RA-DBMM algorithm can effectively improve the problem of data congestion, and improve the reliability and throughput of network.
智能电网具有网络规模大、实时性要求高、拓扑结构固定等特点.相应地,其通信网络需要具备低时延、高可靠、自组织的性质[1-2].在电力通信网中,终端采集的数据需要经过多跳传输到网关节点,靠近网关节点转发的数据相对越多,容易造成其数据缓存的排队等待队列过长而形成拥塞,影响整个网络的吞吐量和有效性[3-6].因此,建立适合电力数据传输特点的路由算法是需要解决的一个重要问题.
为此,在无线网状网络的网络结构的基础上建立了智能电网数据采集网络的数学模型,在距离矢量路由协议(DSDV)中,以每个节点的负载作为路由决策度量值建立了数据平衡路由度量模型DBMM,并提出了RA-DBMM.最后,在Matlab仿真平台下,对RA-DBMM和Bellman-Ford的分组丢失率和时延特性进行了仿真实验.
1 问题模型1.1 问题描述智能电网数据采集系统的网络实体包括智能电表和通信网关,其中智能电表用于收集用电数据并将其转发至对应的通信网关;通信网关用于将汇聚于其上的用电数据转发到电力通信骨干网.靠近网关的智能电表将比远离网关的智能电表负载更多的转发数据,其数据缓存具有更长的排队队列,容易产生拥塞,因而它将成为影响网络吞吐量和时延的瓶颈.由于智能电表的通信距离较短,为每一个智能电表提供一个连接到网关的单跳链路将导致设备复杂度增大、通信质量降低等.为此,文献[4]提出了多跳通信方式,该方式要求智能电表既可以直接向网关上传数据,还可以通过其他智能电表将数据转发至网关,将智能电表作为路由器,以实现分流负载.
1.2 问题模型网络拓扑至少包含一个AP网关节点以及与其通信的若干WR子网,每个子网由多个智能电表构成,并且需要假设所有智能电表到WR的距离小于lmax,lmax为WR有效通信范围内最远智能电表到达该WR的跳数,以保证任意智能电表均能找到至少一条到AP节点的数据采集路由路径.
此外,以智能电表到WR节点的最小跳数为决策参数对网络进行分层:1) 与WR节点直邻的智能电表为第1层节点,即到WR最小跳数为1的智能电表是第1层节点;2) 第1层节点的直邻节点且到WR最小跳数为2的智能电表为第2层节点.依次类推,定义第n-1层节点的直邻节点且到WR最小跳数为n的智能电表为第n层节点.每个节点维护一个初始数据队列即历史数据,其网络结构如图 1所示.为了简化模型,

|
图 1 网络结构 |
假设L层中每个智能电表节点的可通信节点仅包括L层和L-1层的可通信范围内的节点.
将网络结构表示为(N,L),其中节点集合N表示所有通信设备,边集合L表示所有可通信链路.对于节点u, v∈N,用(u, v)表示节点u到节点v的链路.将节点集合N划分为两类,即作为目的节点接收数据的网关节点集合WR和既可以发送数据也可以转发数据的智能电表节点集合M.每个节点v∈N维护一个自身历史数据记录,其内容为节点的缓存队列长度和剩余容量,分别用L (v)和A (v)表示.当A (v)=0时,节点v将成为整个网络的瓶颈.此外,用Times表示周期数,并限定每个发送周期数据分组只能进行单跳传输.同时,假设在一个发送周期内,网络中的任何一个节点都只能发送一个数据分组,且发送过程和接收、缓存过程互不影响.网络中的所有数据流集合表示为F,F中任一数据流表示为f,f∈F. s (f)表示此数据流发送端节点. Dataf[t](f∈F)表示在Times=t时刻被采集进入网络的数据流f所携带的数据分组个数.
DSDV采用Bellman-Ford,以跳数作为度量值,任意两点间的权重为w,两个直邻节点之间的权重为1,即两点间的条数,见式(1).

|
(1) |
从发送节点s到目的节点d的最短路由表示为需要通过最小跳数Hs→dmin 的路径,因此在DSDV路由协议中任意两节点间的度量值Metic定义如下.

|
(2) |
采用式(2) 作为度量值时节点维护的路由表示意图如图 2所示.如果网络拓扑结构未发生变化,则最小跳数不会发生变化.但是,当下一跳节点排队数据队列长度增长时,该方法无法均衡数据流. 图 2(a)表示路由表结构,每个节点维护着到达所有可连通节点的路由信息,包括可到达的节点、到达该节点的最小跳数和下一跳路由节点地址. 图 2(b)为一个lmax=2的网络实例.当数据流f的发送节点为S节点,即s (f)=S时,根据DSDV协议采用Bellman-Ford,Metriv(S, D)=HS→Dmin =2,因此S节点所维护的路由表中目的节点为D的条目中,跳数字段为2,下一跳节点字段为A.如图 2(b)所示实例中的情况,节点S的上一层节点A排队数据队列长度较长且已经接近节点容量,继续向A传送数据更容易形成拥塞.此时,如果选择位于同一层但缓存数列长度较短的节点B进行转发,起到了平衡数据流量,避免关键节点发生拥塞的作用.
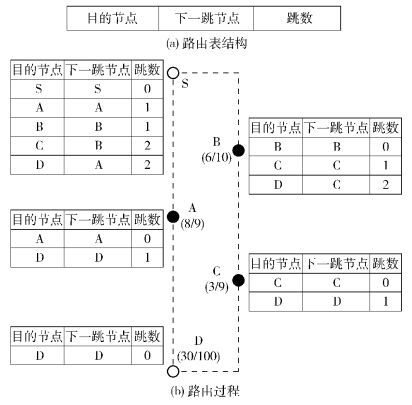
|
图 2 Bellman-Ford |
依据网络拓扑和流量分布信息提出了能够降低网络时延和拥塞的电力通信数据采集路由算法.其思想源自WMNs网络结构下的DSDV,并对DSDV进行了改进,设计了RA-DBMM.
2 基于数据平衡的数据采集路由算法2.1 路由度量模型引入剩余容量来实现数据流量的负载均衡,其定义为转发节点未被占用的容量,即该节点仍可用来存储和转发数据的容量.假设一个节点v的总容量为C (v),已被占用的排队队列长度为Q (v),则可以推断出剩余容量A (v),即节点剩余容量为总容量减去排队队列长度.

|
(3) |
为了解决提出的问题,不仅考虑将跳数作为决策参数,还考虑转发节点的剩余容量.提出了基于剩余容量的数据平衡路由度量模型,该模型将跳数hop和剩余容量A作为决策参数,即由hop和A来计算两点间的权重,如式(4) 所示.

|
(4) |
其中,剩余容量的定义为:
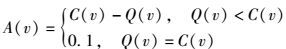
|
(5) |

|
(6) |
由式(4) 和式(5) 便可以得到任意两点间的度量值模型,如式(6).
2.2 路由算法基于RA-DBMM的路由算法如图 3所示,对路由表结构进行了修改,将节点维护的路由表中的跳数字段替换为度量值Metric (S,D),用于对下一跳路由进行决策.对剩余容量进行更新:剩余容量随着数据传输的不断进行,节点完成一次传输将会导致剩余容量的变化,这个变化将改变该节点和转发节点之间的链路权重.同时也会导致该节点的下一跳节点排队队列长度和剩余容量的变化.在DSDV信息更新方法的基础上建立了适用RA-DBMM的路由信息更新机制.在选择数据分组的传输路由时,节点剩余容量的更新过程在路由表被触发更新之前被更新,即每完成一次数据传输都需要先修改相关节点路由表中的Metric字段.随后,才进行路由表被触发的更新,路由选择过程根据更新后的Metric字段重新确定下一跳节点,以此保证基于剩余容量的最新信息.

|
图 3 基于RA-DBMM的路由算法 |
1) 分组丢失率
仿真结果如图 4所示,在仿真开始阶段,网络负载较轻,相较于DSDV路由协议所采用的Bellman-Ford,采用RA-DBMM的分组丢包现象出现较晚.在网络负载低于一定门限的情况下,RA-DBMM对网络瓶颈问题改善明显,性能提升高达80.28%.随着智能电表节点不断增加数据分组,网络负载逐渐增大,超出了网络所能承载的容量,此时分组丢失率趋于稳定,在网络负载与网络容量差值附近波动. RA-DBMM的分组丢失率依然低于原Bellman-Ford,改善比率为16.75%.通过分析可知,在网络负载相同的前提下,RA-DBMM分组丢失率明显低于Bellman-Ford,因此RA-DBMM能够更好地保持网络可靠性,同时承担更大的数据吞吐量.
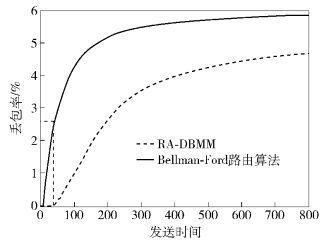
|
图 4 分组丢失率表现 |
2) 平均时延
传输时延主要与跳数相关,排队时延主要表现为节点排队队列长度.假设一个节点到主网关AP节点的数据流f的总时延为Df,则总时延定义如下.
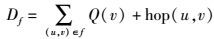
|
(7) |
对仿真区域内所有智能电表节点进行了时延性能仿真,仿真结果如图 5所示,虽然在一开始负载较轻的情况下,RA-DBMM的平均时延相较于Bellman-Ford增大了13.34%.

|
图 5 时延表现 |
为了克服智能电网采集数据汇聚过程中的关键节点拥塞问题,提出了RA-DBMM,加入了剩余容量约束.实验表明:算法在面对不同网络负载量时均能提供更高的网络可靠性和吞吐量,且在负载较重的情况下能够降低时延,提供更好的网络有效性.但是仅针对单一场景进行分析,并未考虑多AP、节点内部排队机制复杂等情况,即仿真实验是在简化的理想状态下进行的,下一步将结合更贴近实际的数据,测试算法的不足并加以完善.
| [1] |
吴小辰. 南方电网"十二五"电力通信发展规划综述[J]. 电力系统通信, 2011, 32(5): 7–9.
Wu Xiaochen. Review of power communication development plan of china southern power grid in the twelfth five-year plan period[J].Telecommunications for Electric Power System, 2011, 32(5): 7–9. |
| [2] |
苗新, 陈希. 电力通信网的安全体系架构[J]. 电力系统通信, 2012, 33(1): 34–38.
Miao Xin, Chen Xi. Security architecture of electric power communication network[J].Telecommunications for Electric Power System, 2012, 33(1): 34–38. |
| [3] | Perkins C E, Bhagwat P. Highly dynamic destination sequence-vector routing (DSDV) for mobile computers[J].Computer Communication Review, 1994, 24(4): 234–244. doi: 10.1145/190809 |
| [4] | Hamid Gharavi, Chong Xu. Traffic scheduling technique for smart grid advanced metering applications[J].IEEE Transactions on Communications, 2012, 60(6): 1646–1658. doi: 10.1109/TCOMM.2012.12.100620 |
| [5] | Bhaya, Gaurav, Manoj B S, et al. Ring based routing schemes for load distribution and throughput improvement in multichip cellular, ad hoc, and mesh networks[C]//Proceedings of 2003 International Conference on High Performance Computing (HiPC'03). India: Springer Berlin Heidelberg, 2003: 152-161. |
| [6] | Hegarty, David F, Tahar Kechadi M. Topology preserving dynamic load balancing for parallel modecular simulations[C]//Supercomputing, ACM/IEEE 1997 Conference. Dublin: IEEE Press, 1997: 36. |


