传统对扩频通信的分析都是从时域进行分析处理的,且相关的分析研究都是针对伪随机码元波形(PCW)采用二值矩形波的. 为此,从干扰和扩频信号频谱重叠的角度对扩频通信的抗干扰误码率(BER)进行分析,提出了频谱重叠度(SOD)的概念. 从频域的角度对BER公式进行分析,使得理论和直观的物理概念一致;给出了BER和SOD的数学表达式,推导证明了BER为SOD的单调递增函数,为扩频系统提供了一个规避干扰的扩频信号设计准则. 此外,给出了任意伪随机码元波形下扩频通信系统的BER性能分析. 实验结果验证了SOD理论的正确性.
The classic bit error rate (BER) performance analysis comes from the time domain and the existing research aimed at the condition of rectangular pseudo-random code waveform (PCW). A method was proposed to analyze the BER performance of the spread-spectrum system by the overlap between the spectrum of the spread-spectrum signals and the interference. The concept of spectrum overlap degree (SOD) was given. It can make theory analysis and intuitionistic physical conception consistent so that the BER in the frequency domain can be deduced. Besides, the mathematical expression of BER and SOD was given and BER was proved to be proportional to SOD. Analysis and derivation about SOD gives a criterion to design spread spectrum signal to avoid interference. Furthermore, The given BER is suitable for arbitrary PCW. The validity about SOD was verified through simulation.
在以往对扩频通信的研究中,对扩频通信系统的误码率(BER,bit error rate)性能分析都是从时域进行的[1, 2]. 并且,其采用的伪随机码元波形(PCW,pseudo-random code waveform)都是矩形波[3, 4]. 但在实际的应用中,受带宽等特定条件的限制,PCW不再局限于矩形波[5, 6, 7]. 但对于这样的扩频通信,很少进行过BER性能的分析.
为此,笔者通过推导给出了任意PCW下的扩频通信系统的BER公式,提出了频谱重叠度(SOD,spectrum overlap degree)的概念,并给出了BER与SOD的数学表达式,推导证明了BER是SOD的单调递增函数.
1 理论推导图 1为直扩通信的最佳接收机收发框图. 其中,载波频率为f0;伪随机码元持续时间为Tc;离散信源集合为{an};每个信源符号持续时间为T;w(t)表示信源波形样本,通常w(t)为方波,即
| $ w\left( t \right) = \left\{ \begin{array}{l} 1,\;\;\;0 \le t \le T\\ 0,\;\;\;其他 \end{array} \right. $ | (1) |
发射端的射频信号为
| $ s\left( t \right) = {a_n}w\left( t \right){P_N}\cos {\omega _0}t $ | (2) |
其中:ω0为载波角频率;PN(t)为选定的直扩信号,采用长度为N的m序列. 因此,PN(t)在T之外的时域内取值为0. 设定每个信源符号包含一个伪随机序列,则信源宽度T=NTc.
| $ {P_N}\left( t \right) = {c_n}\left( t \right)*h\left( t \right) = \sum\limits_{n = 0}^{N - 1} {{c_n}h\left( {t - n{T_c}} \right)} $ | (3) |
其中: $ {c_n}\left( t \right) = \sum\limits_{n = 0}^{N - 1} {{c_n}\delta \left( {t - n{T_c}} \right)} $为扩频用的伪随机序列,h(t)为扩频用的PCW成型函数.
在接收端都是针对每个信源符号进行的接收判决,因此,当分析系统的BER性能时主要针对单个符号内分析和推导. 对于一个信源符号内,发送端信号为
| $ s\left( t \right) = {a_i}{P_N}\left( t \right)\cos {\omega _0}t $ | (4) |
其中:0≤t≤T,ai∈{an}={±A}(A为信源的幅度).
对任意PCW,令 $ {E_{PN}} = \int_0^T {P_N^2\left( t \right)dt} $,则信源比特能量为
| $ {E_b} = E\left[ {{s^2}\left( t \right)} \right] = E\left[ {\alpha _i^2P_N^2\left( t \right){{\cos }^2}{\omega _0}t} \right] = {A^2}{E_{PN}}/2 $ | (5) |
图 1中匹配滤波输出为
| $ \begin{array}{l} r\left( t \right) = \int_0^T {x\left( t \right)\left[ {{P_N}\left( t \right) \times 2\cos {\omega _0}tw\left( t \right)} \right]} dt = \\ \underbrace {\int_0^T {s\left( t \right)\left[ {{P_N}\left( t \right) \times 2\cos {\omega _0}t} \right]dt} }_{{S_t}} + \\ \underbrace {\int_0^T {i\left( t \right)\left[ {{P_N}\left( t \right) \times 2\cos {\omega _0}t} \right]dt} }_{{S_t}} + \\ \underbrace {\int_0^T {n\left( t \right)\left[ {{P_N}\left( t \right) \times 2\cos {\omega _0}t} \right]dt} }_{{N_t}} \end{array} $ | (6) |
可见,经过最佳接收机后被用来判决的r(t)包含3部分:St、Nt和It.
将式(4)代入St,可得
| $ \begin{array}{l} {S_t} = {a_i}\int_0^T {P_N^2\left( t \right)dt + } {a_i}\int_0^T {P_N^2\left( t \right)\cos 2{\omega _0}} = \\ {a_i}\int_0^T {P_N^2\left( t \right)dt} = {a_i}{E_{PN}} \end{array} $ | (7) |
对Nt的分析可得[8]
| $ {N_t} \sim N\left( {0,{n_0}{E_{PN}}} \right) $ | (8) |
不存在干扰:发送0码时,r(t)~N(-AEPN,n0EPN);发送1码时,r(t)~N(AEPN,n0EPN). 可以得到扩频系统采用任意PCW时的系统BER为
| $ {P_e} = \frac{1}{2}erfc\left( {\sqrt {\frac{{{A^2}{E_{PN}}}}{{2{n_0}}}} } \right) = \frac{1}{2}erfc\left( {\sqrt {\frac{{{E_b}}}{{{n_0}}}} } \right) $ | (9) |
其中 $ erfc\left( x \right) = \frac{2}{{\sqrt \pi }}\int_x^\infty {{e^{ - {y^2}}}} dy $.
存在干扰i(t):发送0码时,r(t)~N(It-AEPN,n0EPN);发送1码时,r(t)~N(It+AEPN,n0EPN). 此时BER为
| $ \begin{array}{l} {P_e} = \frac{1}{4}\left\{ {erfc\left( {\sqrt {\frac{{{A^2}{E_{PN}}}}{{2{n_0}}}} - \frac{{{I_t}}}{{\sqrt {2{n_0}{E_{PN}}} }}} \right) + } \right.\\ e\left. {rfc\left( {\sqrt {\frac{{{A^2}{E_{PN}}}}{{2{n_0}}}} + \frac{{{I_t}}}{{\sqrt {2{n_0}{E_{PN}}} }}} \right)} \right\} \end{array} $ | (10) |
为了便于推导,将信源幅值进行归一化处理,即令A=1,此时由式(5)得
| $ {E_b} = {A^2}{E_{PN}}/2 = {E_{PN}}/2 $ | (11) |
因此,式(10)可以简化为
| $ \begin{array}{l} {P_e} = \frac{1}{4}\left\{ {erfc\left[ {\sqrt {\frac{{{E_b}}}{{{n_0}}}} \left( {1 - \frac{{{I_t}}}{{2{E_b}}}} \right)} \right]} \right. + \\ erfc\left. {\left[ {\sqrt {\frac{{{E_b}}}{{{n_0}}}} \left( {1 + \frac{{{I_t}}}{{2{E_b}}}} \right)} \right]} \right\} \end{array} $ | (12) |
式(12)为任意PCW时扩频通信的BER公式. 可以看出,式(12)适用于任意PCW的扩频系统,只与干扰项It有关. 当系统中出现不同的干扰i(t)时,只需要把相应的It代入式(12),就可以得到当前i(t)下系统BER的表达形式. 下面就给出不同类型的输入干扰i(t)时,最佳接收机输出的干扰分量It的化简分析. 由式(6)的It部分得
| $ \begin{array}{l} {I_t} = 2\int_0^T {P_N^2\left( t \right)i\left( t \right)} \cos {\omega _0}tdt\\ 2\int_{ - \infty }^\infty {P_N^2\left( t \right)} i\left( t \right)\cos {\omega _0}tdt \end{array} $ | (13) |
对于频率为fI的干扰i(t)来说,当其位于发送端信号的主瓣内时才会对发送信号形成干扰,即 Δf=|fI-f0|<fc(fc为载波频率),Δω=|ωI-ω0|<ωc(ωI 为干扰角频率,ωc为载波角频率). 对It的化简,可以从以下两方面进行.
1) 对于单频干扰,当i(t)=αcos (ωIt+θ)(α为单频干扰幅度,θ为附加相位)时,有
| $ {I_t} = \frac{1}{{2\pi }}\int_{ - \infty }^\infty {{P_N}\left( {j\omega } \right)} {\left[ {I\left( {j\left( {\omega + {\omega _0}} \right)} \right) + I\left( {j\left( {\omega - {\omega _0}} \right)} \right)} \right]^ * }d\omega $ | (14) |
2) 当i(t)为非周期窄带干扰时,有
| $ \begin{array}{l} {I_t} = \frac{1}{2}\left[ {{e^{ - j\theta }}{P_N}\left( {j\Delta \omega } \right) + {e^{j\theta }}{P_N}\left( { - j\Delta \omega } \right)} \right] = \\ \;\;\;\;\;\;\alpha {\mathop{\rm Re}\nolimits} \left\{ {{e^{ - j\theta }}{P_N}\left( {j\Delta \omega } \right)} \right\} \end{array} $ | (15) |
把上述中不同i(t)下的It化简结果带入BER通式中,即可得到当前i(t)的BER表达式.
2 SOD的推导分析分析式(15)的化简结果,其中的I(j(ω+ω0))+I(j(ω-ω0))恰好代表i(t)cos ω0t的频谱,即干扰i(t)频谱的线性搬移,而PN(jω)代表的是PN(t)的频谱. It的化简结果说明,只有i(t)cos ω0t与PN(t)的频谱存在重叠时,It才不为0. 对于式(14)的化简结果分析也是如此. 因此,把 $ \left| {\frac{{{I_t}}}{{2{E_b}}}} \right| $称为SOD.
令β= $ \left| {\frac{{{I_t}}}{{2{E_b}}}} \right| $表示SOD,$k = \sqrt {{E_b}/{n_0}} $,则式(12)可简化为
| $ {P_e}\left( \beta \right) = \frac{1}{4}\left[ {2 - erf\left( {k\left( {1 - \beta } \right)} \right) - erf\left( {k\left( {1 + \beta } \right)} \right)} \right] $ | (16) |
两边求导可得
| $ \frac{d}{{d\beta }}{P_e}\left( \beta \right) = \frac{k}{{2\sqrt \pi }}\left[ {{e^{ - {k^2}{{\left( {1 - \beta } \right)}^2}}} - {e^{ - {k^2}{{\left( {1 + \beta } \right)}^2}}}} \right] $ | (17) |
分析式(17)可知,对于β≥0,BER是重叠度的单调递增函数,并且β=0时,BER取得最小值. 这个结果证实了干扰和扩频信号的频谱重叠越严重,系统的BER性能越差.
3 仿真结果在仿真中,扩频序列采用长度N=15的m序列. SOD理论公式与PCW无关,因此仿真实验的PCW采用矩形波即可. 伪随机码元持续时间为Tc,且有fc=1/Tc,则发射端的信号带宽为Bc=2fc. 载波频率为f0,且窄带干扰采用二进制相移键控(BPSK,binary phase shift keying)信号,其带宽BBPSK=0.2Bc. 信号功率与噪声功率之比采用Eb/EI表示,其中EI为单位比特内干扰的能量. 实验所有的仿真结果均是基于Matlab软件仿真得到的. 总体共分为两大部分,分别是单频和BPSK干扰下的仿真结果,每部分分别包含了信噪比BER曲线和信干比BER曲线. 其中,两部分的信干比BER仿真中,信干比Eb/EI=-10dB;信噪比BER仿真中,信噪比Eb/n0=5dB. 信噪比BER和信干比BER仿真结果均分别包含了干扰中心频率为f0+0.2fc、f0+0.4fc和f0+0.6fc 3种干扰下的仿真结果. 在所有的仿真图中,用fI表示干扰的中心频率.
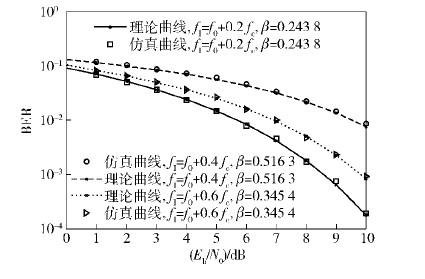
3.1 单频干扰下图 2和 图 3分别给出了单频干扰下直扩通信最佳接收机的信噪比BER和信干比BER曲线,最重要的是给出了每种情况下的SOD值,并给出了不同频点处的理论曲线和实际仿真曲线.
由 图 2可以看出,不同频点的干扰存在时,相应的SOD值也不同;还可以看出,SOD值越大,BER越大. 而且,理论曲线和实际曲线的重合证实了前面单频干扰下理论推导的正确性,进一步证实了直观意义上的单频干扰和扩频信号重叠得越严重,通信系统的BER性能越差. 相对于图 2给出的不同频率单频干扰下的信噪比BER性能对比,图 3给出了信干比BER性能对比. 图 3理论曲线和实际仿真曲线的重合进一步证实了单频干扰下SOD理论公式推导的正确性.
3.2 窄带干扰下相对于3.1节给出的单频干扰下关于SOD理论推导正确性的仿真验证,本节将给出BPSK干扰下SOD理论的仿真验证. 同样地, 图 4和 图 5分别给出了BPSK干扰下直扩通信系统最佳接收机的信噪比BER和信干比BER曲线.
由图 4和图 5可以看出,在BPSK干扰下,理论曲线和实际曲线的重合证实了关于窄带干扰下SOD理论推导的正确性. 并且通过图 4的仿真曲线可以看出,SOD值越大,BER越差,证实了直观意义上的干扰和扩频信号重叠得越严重,通信系统的BER性能越差.
4 结束语笔者推导出了干扰存在时任意PCW下扩频通信的BER公式,通过对BER公式中的干扰项进行分析,提出了SOD的概念,并给出了BER和SOD的数学关系式,而且推导证明出BER是SOD的单调递增函数,即SOD越大,BER越大. 这一结论证实了直观上的概念,即发射信号和干扰频谱重叠越严重,系统的通信性能越差. 不同中心频率的单频和BPSK干扰下理论和实际仿真曲线的重合证实了理论推导SOD公式的正确性. SOD概念的理论分析和推导为扩频系统提供了一个规避干扰的扩频信号设计准则:若设计出的扩频信号能够在强干扰频段处形成零陷,就能最大限度地降低SOD,从而让系统BER性能达到最佳.
| [1] | 褚振勇, 易克初, 田红心. 直接序列扩频信号的时频特性分析[J]. 电路与系统学报, 2004, 9(3): 23-28. Chu Zhenyong, Yi Kechu, Tian Hongxin. Time-frequency analysis of the direct sequence spread spectrum signals[J]. Journal of Circuits and Systems, 2004, 9(3): 23-28.[引用本文:1] |
| [2] | Fuxjaeger A W, Iltis R A. Acquisition of timing and Doppler-shift in a direct-sequence spread-spectrum system[J]. IEEE Transactions on Communications, 1994, 42(10): 2870-2880.[引用本文:1] |
| [3] | Lee Chieho, Chang Chungju. An accurate method for approximating the interference statistics of DS/CDMA cellular systems with power control over frequency-selective fading channels [J]. IEEE Communications Letters, 2005, 9(1): 28-30.[引用本文:1] |
| [4] | Cho J H, Lehnert J S. An optimal signal design for band-limited asynchronous DS-CDMA communications [J]. IEEE Transactions on Information Theory, 2002, 48(5): 1172-1185.[引用本文:1] |
| [5] | Gao Wen, Cho J H, Lehnert J S. Chip waveform design for DS/SSMA systems with aperiodic random spreading sequences [J]. IEEE Transactions on Wireless Communications, 2002, 1(1): 37-45.[引用本文:1] |
| [6] | Zang Guozhen, Ling Cong. Performance evaluation for band-limited DS-CDMA systems based on simplified improved gaussian approximation [J]. IEEE Transactions on Communications, 2003, 51(7): 1204-1213.[引用本文:1] |
| [7] | Luo Tao, Pasupathy S, Sousa E S. Interference control and chip waveform design in multirate DS-CDMA communication systems [J]. IEEE Transactions on Wireless Communications, 2002, 1(1): 56-66.[引用本文:1] |
| [8] | Schilling D L, Milstein L B, Pickholtz R L, et al. Optimization of the processing gain of an M-ary direct sequence spread spectrum communication system [J]. IEEE Transactions on Communications, 1980, 28(8): 1389-1398.[引用本文:1] |