引用本文
谢显中, 王闯, 张森林, 葛振涛. 基于干扰对齐的多用户全双工通信中干扰消除方法[J]. 北京邮电大学学报, 2015, 38(6): 87-92.  
XIE Xian-zhong, WANG Chuang, ZHANG Sen-lin, GE Zhen-tao. Interference Cancellation Based on Interference Alignment for Multiuser Full-Duplex Communications[J]. JOURNAL OF BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS, 2015, 38(6): 87-92.  
Permissions
Copyright©2015, 《北京邮电大学学报》编辑部
《北京邮电大学学报》编辑部 所有
基于干扰对齐的多用户全双工通信中干扰消除方法
谢显中, 王闯, 张森林, 葛振涛    
重庆邮电大学 个人通信研究所, 重庆 400065
作者简介: 谢显中(1966—),男,教授,博士生导师,E-mail:xiezh@cqupt.edu.cn.
收稿日期: 2014-11-22
基金项目: 国家自然科学基金项目(61271259,61301123);重庆市自然科学基金项目(CTSC2011jjA40006);重庆市教委科学技术研究项目(KJ120501,KJ130536)
摘要

为了消除多用户全双工干扰信道中的自干扰和互干扰,将干扰对齐思想应用于全双工干扰信道中. 根据多用户全双工模型的特性将其等效为单向信道模型,并给出了等效模型与原模型之间的信道矩阵对应关系;基于此等效模型和信道矩阵对应关系,应用迭代干扰对齐和最大信干噪比方法将其自干扰和互干扰消除;干扰泄漏功率的仿真结果验证了算法的有效性和正确性,系统容量和平均能量效率也较其他算法都有明显提高.

关键词: 多用户全双工干扰信道    干扰对齐    最大信干噪比    容量    平均能量效率         
中图分类号: TN929.53 文献标志码:A 文章编号:1007-5321-38-6-87 DOI:10.13190/j.jbupt.2015.06.018
Interference Cancellation Based on Interference Alignment for Multiuser Full-Duplex Communications
XIE Xian-zhong, WANG Chuang, ZHANG Sen-lin, GE Zhen-tao    
Institute of Personal Communication, Chongqing University of Posts and Telecommunications, Chongqing 400065, China
Abstract

There exist self-interference and mutual interference in multiuser full-duplex system. The interference alignment technique (IA) is applied to eliminate both self-interference and mutual interference in multiuser full-duplex communication. According to the characteristics of the multiuser full-duplex system, it is treated as a one-way channel model and the channel matrix of the corresponding relationship between the equivalent model and the original model is given. Based on this thoughtfulness, the minimum interference leakage alignment (Min-IL) and the maximum signal to interference plus noise ratio algorithm (Max-SINR) were presented to eliminate both self-interference and mutual interference in multiuser full-duplex communications. Simulation proves that the proposed algorithms are effective. Comparing with other schemes, both the system capacity and the average energy efficiency are improved obviously by the proposed schemes.

Key words: multiuser full-duplex interference channel    interference alignment    maximum signal to interference plus noise ratio    capacity    average energy efficiency    

同频同时全双工(CCFD，co-frequency co-time full duplex)无线通信设备使用相同的时间和相同的频率，同时发射和接收无线信号. 与现有的频分双工(FDD,frequency division duplexing)或时分双工(TDD,time division duplexing)等双工方式相比，CCFD能够将无线资源的使用率提升近一倍，作为5G的潜在关键技术，目前CCFD受到了广泛关注[1]. 由于收发同时同频，CCFD设备具有很强的自干扰，使用CCFD的首要工作是抑制强自干扰.

国内外研究人员已对CCFD的自干扰消除进行了大量研究[2]，目前主要涉及3种方案，即天线干扰消除[3]、射频干扰消除[4]、数字干扰消除[5]. 实际上，在CCFD中除了自干扰问题也存在互干扰问题，比如在采用小蜂窝(Small Cell)组网的环境、无线设备到设备(Device-to-Device)通信场景等[6]，上述研究并没有同时解决CCFD的自干扰和互干扰问题，此外，上述干扰消除方案并没有涉及干扰对齐的思想，而笔者考虑将干扰对齐应用于全双工的自干扰和互干扰消除. 如果能实现完全干扰消除，其系统总速率会有更大提升.

干扰对齐(IA，interference alignment)基本思想是当来自所有其他非期望发射端的干扰信号远远大于接收端所接收的信号时，通过在发送端设计合理的预编码矩阵Vk，来压缩对非期望接收端造成的干扰，进而保证接收到的期望信号与干扰子空间保持线性独立，然后在接收端设计相应的干扰抑制矩阵Uk来迫除干扰信号，这样即可解码出无干扰的期望信号. 分布式迭代干扰对齐算法仅需要局部状态信息(CSI,channel state information)，不论是在高信噪比(SNR,signal-to-noise ratio)还是在低信噪比下都可以显著提高系统的信道容量[7].

针对相邻小蜂窝同频组网的多用户全双工通信干扰信道场景，在同时考虑自干扰和互干扰情况下将其等效为单向信道模型，并给出等效模型与原模型之间的信道矩阵对应关系；然后，基于此等效模型和信道矩阵对应关系，应用迭代干扰对齐方法将其自干扰和互干扰消除.

1 全双工通信干扰信道的等效模型 1.1 多用户全双工通信干扰信道

考虑相邻小蜂窝同频组网的多用户全双工通信干扰信道，即用户与基站都是工作在全双工模式下. 假设用户ui(i=1,2,…,K)只期望接收来自对应基站bi的信号，也只打算把信号发给对应基站bi，同时把其他基站和其他用户发送的信号以及自身发送的信号看作干扰信号，并且对其他用户和其他基站以及自身接收端产生干扰，在这里统称为干扰信号. 同样，基站bi只期望接收来自对应用户ui的信号，也只打算把信号发给对应用户ui，同时把其他基站和其他用户发送的信号以及自身发送的信号看作干扰信号，并且对其他用户和其他基站以及自身接收端产生干扰. 如图 1为多用户全双工通信干扰信道模型.

图1 多用户全双工通信干扰信道

假设基站配置M根天线，用户配置N根天线. 对于用户ui的接收端，定义Hjibu∈CM×M为基站bj的发射端到用户接收端的信道矩阵，Hjiuu∈CM×M为用户uj的发射端到用户ui接收端的信道矩阵. 假设信道为平坦瑞利信道，信道中各元素独立分布，服从均值为0和方差为1的复高斯分布. 则用户接收端ui接收到的信号为

$\begin{gathered} y_i^u = \sum\limits_{i = 1}^K {H_{ji}^{bu}s_j^b} + \sum\limits_{i = 1}^K {H_{ji}^{uu}s_j^u} + {n_i} = \hfill \\ H_{ii}^{bu}s_i^b\left( {\sum\limits_{j = i,j \ne i}^K {H_{ji}^{bu}s_j^b} + \sum\limits_{j = 1}^K {H_{ji}^{uu}s_j^u} } \right) + n_i^u \hfill \\ \end{gathered} $ (1)
其中：K为用户数和基站数，sju∈CM×1为用户uj的发送信号矢量，sjb∈CM×1为基站bj的发送信号矢量，且均满足约束条件E{sjuHsju}=Pju(Pju表示用户uj的发送功率)，E{sjbHsjb}=Pjb(Pjb表示基站bj的发送功率)，niu为用户接收端ui的加性复高斯白噪声矢量(AWGN)，其分布满足niu～CN(0,σ2I).

同样，对于基站接收端bi，定义Hjiub∈CM×M为用户发射端uj到基站接收端bi的信道矩阵； Hjibb∈CM×M为基站发射端bj基站接收端bi的信道矩阵. 假设信道为平坦瑞利信道，信道中元素独立分布，服从均值为0和方差为1的复高斯分布. 则基站接收端bi接收到的信号为

$\begin{gathered} y_i^b = \sum\limits_{i = 1}^K {H_{ji}^{ub}s_j^u} + \sum\limits_{i = 1}^K {H_{ji}^{bb}s_j^b} + {n_i} = \hfill \\ H_{ii}^{ub}s_i^u\left( {\sum\limits_{j = i,j \ne i}^K {H_{ji}^{ub}s_j^u} + \sum\limits_{j = 1}^K {H_{ji}^{bb}s_j^b} } \right) + n_i^b \hfill \\ \end{gathered} $ (2)
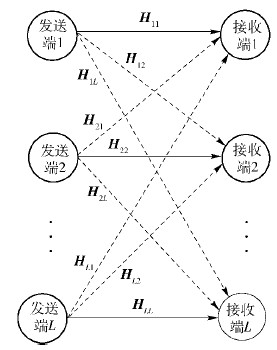
其中：nib为基站接收端的加性复高斯白噪声矢量(AWGN)，其分布满足nib~CN(0,σ2I).

1.2 等效系统模型

由于图 1中的模型较为复杂，为此，将K个用户链路对的全双工干扰信道模型，用L个用户链路对的半双工干扰信道模型进行等效处理，即将图 1中原始模型等效为一个拥有L个半双工源节点和L个半双工目的节点的网络，其中L=2K. 如图 2所示多用户全双工通信模型的等效模型，其中实线对应于期望信号信道，虚线对应于干扰信号信道.

在等效模型中共有L个发送端和L个接收端，每个发送端Tj(j=1,2,…,L)只期望把信号发给与其相对应的接收端Ri(i=1,2,…,L)，并且对其他所有接收端造成干扰；每个接收端Ri也只期望接收与其相对应的发送端Tj的信号，并且受到其他所有发送端的干扰. 这样，对于图 2所示的等效模型，可以运用干扰对齐思想消除干扰(包括自干扰和互干扰).

图2 多用户全双工通信干扰信道的等效信道

根据等效模型和多用户全双工模型，发送端与接收端、发送信号与接收信号的对应关系如下：

当j=1,3,…,$\frac{L}{2}$+1为奇数时，等效模型发送端Tj的发送信号sj对应基站bi发送端的发送信号sib，接收端Rj的接收信号yj对应用户ui接收端的接收信号yiu；当j=2,4,…,$\frac{L}{2}$为偶数时，等效模型发送端Tj对应用户ui发送端的发送信号siu，接收端Rj的接收信号yj对应基站bi接收端的接收信号yib.

定义Hji表示发送端Tj(j=1,2,…,L)到接收端Ri(i=1,2,…,L)的信道矩阵，sj表示发送端Tj发送的信号，yi表示接收端Ri接收的信号. 则等效模型与原模型的信道矩阵对应关系为

$\begin{gathered} {H_{11}} = H_{11}^{bu},{H_{12}} = H_{11}^{bb},{H_{13}} = H_{12}^{bu},{H_{14}} = H_{12}^{bb} \hfill \\ {H_{21}} = H_{11}^{uu},{H_{22}} = H_{11}^{ub},{H_{23}} = H_{12}^{uu},{H_{24}} = H_{12}^{ub} \hfill \\ \vdots \hfill \\ {H_{a1}} = H_{k1}^{bu},{H_{a2}} = H_{k1}^{bb},{H_{a3}} = H_{k2}^{bu},{H_{a4}} = H_{k2}^{bb} \hfill \\ {H_{b1}} = H_{k1}^{uu},{H_{b2}} = H_{k1}^{ub},{H_{b3}} = H_{k2}^{uu},{H_{b4}} = H_{k2}^{ub} \hfill \\ \vdots \hfill \\ {H_{L - 1,1}} = H_{K1}^{bu},{H_{L - 1,2}} = H_{K1}^{bb},{H_{L - 1,3}} = H_{K2}^{bu},{H_{L - 1,4}} = H_{K4}^{bb} \hfill \\ {H_{L1}} = H_{K1}^{uu},{H_{L2}} = H_{K1}^{ub},{H_{L3}} = H_{K2}^{uu},{H_{L4}} = H_{K2}^{ub} \hfill \\ \end{gathered} $ (3)
其中：a=2k-1,b=2k,k=1,2,…,K.

根据上述对应关系以及式(1)~(3)可得出等效的接收信号(矢量)为

${y_i} = \sum\limits_{j = 1}^K {{H_{ji}}{s_j}} + {n_i} + \sum\limits_{j = 1j \ne 1}^K {{H_{ji}}{s_j}} + {n_i}$ (4)

该等效模型与一般K用户多输入多输出(MIMO,multiple-input multiple-output)干扰信道模型有实质性的差别. 对于一般的K用户MIMO干扰信道中每个接收端的干扰来自其他发送端的发送信号，并且是K用户之间的相互干扰. 而等效模型表面看上去与一般K用户MIMO干扰信道模型相似，但它的本质是多用户全双工通信干扰信道，因此，在等效模型中的干扰不仅包含有不同用户之间、不同基站之间及用户与基站之间的互干扰，还包括全双工通信时用户之间的自干扰、基站之间的自干扰，即用户或基站自身发送端对自身接收端的干扰. 所以，在等效信道中的部分信道具有互惠性，于是，以K=2为例得到信道矩阵满足的关系：

$\begin{align} & {{H}_{11}}={{H}_{22}},{{H}_{12}}={{H}_{12}},{{H}_{13}}={{H}_{42}},{{H}_{14}}={{H}_{32}},{{H}_{21}}={{H}_{21}} \\ & {{H}_{23}}={{H}_{41}},{{H}_{24}}={{H}_{31}},{{H}_{33}}={{H}_{44}},{{H}_{34}}={{H}_{34}},{{H}_{43}}={{H}_{43}} \\ \end{align}$ (5)

2 干扰对齐算法

干扰对齐是用于消除通信系统中发送端的发送信号对非期望接收端所造成的干扰，即在接收端消除非期望发送端发送的非期望信号. 而多用户全双工通信中的互干扰就是基站或用户的非期望发送端的发送信号所造成的干扰，对于自干扰其实质上是基站或用户本身发送给其期望接收端的有用信号，由于系统处于全双工通信模式，该“有用信号”对其自身接收端来说就是不希望接收的“有用信号”. 这与其他非期望用户和基站的发送信号所带来的干扰其实质是属于同一种类型的干扰，即非期望干扰信号. 因此，可以用干扰对齐来消除多用户全双工通信中的互干扰和自干扰.

2.1 迭代干扰对齐算法

将基站到用户的链路称为正向链路，用户到基站的链路称为逆向链路. 在正向链路传输时，第i用户ui(i=1,2,…,K)的接收端接收到信号为

${y_i} = \sum\limits_{j = i}^K {{H_{ji}}} {V_j}{s_j} + {n_i} = \underbrace {{H_{ii}}{V_i}{s_i}}_{期望信号} + \underbrace {\sum\limits_{j = 1,j \ne i}^K {{H_{ji}}} {V_j}{s_j} + {n_i}}_{干扰信号}$ (6)
其中：yi为Nt×1维接收信号；Vi为Nr×d(i)维预编码矩阵；sj为d(i)×1维信号矢量；ni为Nt×1维加性复高斯白噪声矢量，其分布满足ni~CN(0,σ2I)；Hji为Nt×Nr维信道增益矩阵.

利用信道互惠性，在逆向传输时，第i基站bi(i=1,2,…,K)的接收端接收到信号(矢量)为

$\overleftarrow {{y_i}} = \sum\limits_{j = i}^K {{{\overleftarrow H }_{ji}}} {\overleftarrow V _j}{\overleftarrow s _j} + {\overleftarrow n _i} = \underbrace {{{\overleftarrow H }_{ii}}{{\overleftarrow V }_i}{{\overleftarrow s }_i}}_{期望信号} + \underbrace {\sum\limits_{j = 1,j \ne i}^K {{{\overleftarrow H }_{ji}}} {{\overleftarrow V }_j}{{\overleftarrow s }_j} + {{\overleftarrow n }_i}}_{干扰信号}$ (7)
其中：$\overleftarrow {{y_i}} $为Nr×1维接收信号；$\overleftarrow {{V_i}} $为Nt×d(i)维预编码矩阵；$\overleftarrow {{s_j}} $为d(i)×1维信号矢量；$\overleftarrow {{n_i}} $为Nr×1维加性复高斯白噪声矢量，其分布满足$\overleftarrow {{n_i}} $~CN(0,σ2I)；$\overleftarrow {{H_{ji}}} $为Nr×Nt维逆向信道增益矩阵.

由信道系数互惠关系式(5)可得Hji与Hji满足如下关系：

$\begin{align} & {{\overleftarrow{H}}_{11}}={{H}_{22}},{{\overleftarrow{H}}_{12}}={{H}_{12}},{{\overleftarrow{H}}_{13}}={{H}_{24}},{{\overleftarrow{H}}_{14}}={{H}_{23}} \\ & {{\overleftarrow{H}}_{21}}={{H}_{12}},{{\overleftarrow{H}}_{22}}={{H}_{11}},{{\overleftarrow{H}}_{23}}={{H}_{14}},{{\overleftarrow{H}}_{24}}={{H}_{13}} \\ & {{\overleftarrow{H}}_{31}}={{H}_{42}},{{\overleftarrow{H}}_{32}}={{H}_{41}},{{\overleftarrow{H}}_{33}}={{H}_{44}},{{\overleftarrow{H}}_{34}}={{H}_{43}} \\ & {{\overleftarrow{H}}_{41}}={{H}_{32}},{{\overleftarrow{H}}_{42}}={{H}_{31}},{{\overleftarrow{H}}_{43}}={{H}_{34}},{{\overleftarrow{H}}_{44}}={{H}_{33}} \\ \end{align}$ (8)

此外，对于逆向链路信道，在干扰完全对齐到干扰抑制矩阵零空间后，依然满足以下约束条件：

$\overleftarrow{U}_{j}^{H}{{\overleftarrow{H}}_{ji}}{{\overleftarrow{V}}_{i}}=0,\forall j\ne i$ (9)
$\text{rank}\left( \overleftarrow{U}_{j}^{H}{{\overleftarrow{H}}_{ji}}{{\overleftarrow{V}}_{i}} \right)=d\left( i \right)$ (10)
其中：$\overleftarrow {{V_i}} $和$\overleftarrow {{U_i}} $分别为逆向信道中的预编码矩阵和干扰抑制矩阵，由信道互惠性得$\overleftarrow {{V_i}} $=Ui,$\overleftarrow {{U_i}} $=Vi.

针对多用户全双工等效模型，可以利用文献[8]中所涉及的迭代干扰对齐算法来求取预编码矩阵和干扰抑制矩阵. 首先任意选取Vi和Ui，然后对其进行迭代更新来接近干扰对齐. 这种迭代干扰对齐算法的好坏由接收端的干扰泄漏功率来衡量，其目标就是使得干扰泄漏功率最小化，最终干扰泄漏功率为0. 因此在接收端i，非期望发送端j(j≠i)给其带来的干扰泄漏功率可以表示为

${{I}_{\Delta i}}=\text{Tr}\left( U_{i}^{H}{{Q}_{i}}{{U}_{i}} \right)$ (11)
其中：Tr(A)表示矩阵A的迹，Qi为干扰协方差，其具体表示为
${{Q}_{i}}=\sum\limits_{j=i,j\ne i}^{K}{\frac{P\left( j \right)}{d\left( j \right)}{{H}_{ji}}{{V}_{i}}V_{j}^{H}H_{ji}^{H}}$ (12)

对于逆向信道的接收端的干扰泄漏功率为

${{\overleftarrow{I}}_{\Delta i}}=Tr\left( \overleftarrow{U}_{i}^{H}{{\overleftarrow{Q}}_{i}}{{\overleftarrow{U}}_{i}} \right)$ (13)
其中：Qi为逆向信道中的干扰协方差，其具体表示为
${{\overleftarrow{Q}}_{i}}=\sum\limits_{j=i,j\ne i}^{K}{\frac{\overleftarrow{P}\left( j \right)}{d\left( j \right)}{{\overleftarrow{H}}_{ji}}{{\overleftarrow{V}}_{i}}\overleftarrow{V}_{j}^{H}\overleftarrow{H}_{ji}^{H}}$ (14)

在原始信道和逆向信道中的目标就是最小化IΔi和$\overleftarrow I $Δi，其迭代干扰对齐(最小干扰泄漏min_IL)算法步骤如下.

1) 在发送端随机初始化预编码矩阵Vj.

2) 开始迭代，计算接收端i的干扰协方差：

${{Q}_{i}}=\sum\limits_{j=i,j\ne i}^{K}{\frac{P\left( j \right)}{d\left( j \right)}{{H}_{ji}}{{V}_{i}}V_{j}^{H}H_{ji}^{H}}$

3) 计算干扰抑制矩阵：

${{U}_{i}}=v_{d}^{\min }\left[ {{Q}_{i}} \right]$
其中：vdmin[A]表示矩阵A最小的d个特征值对应的特征向量.

4) 逆向通信，此时令Vi=Ui.

5) 计算逆通信接收端的干扰协方差：

${{\overleftarrow{Q}}_{i}}=\sum\limits_{j=i,j\ne i}^{K}{\frac{\overleftarrow{P}\left( j \right)}{d\left( j \right)}{{\overleftarrow{H}}_{ji}}{{\overleftarrow{V}}_{i}}\overleftarrow{V}_{j}^{H}\overleftarrow{H}_{ji}^{H}}$

6) 计算逆向通信中的干扰抑制矩阵(即正向通信的预编码矩阵)：

${{\overleftarrow{U}}_{i}}=v_{d}^{\min }\left[ {{\overleftarrow{Q}}_{i}} \right]$

7) 反转通信，令Vi=$\overleftarrow U $i.

8) 迭代直到收敛.

2.2 最大信干噪比算法

在上面的迭代算法中，没有考虑期望信号的路径，因此使得接收端的信干噪比(SINR,signal to interference plus noise ratio)不是最优的. 虽然在高信噪比下对和速率几乎无影响，但是在小信噪比时却有很大的影响，进一步考虑接收端i的第k(1≤k≤d(i))个数据流的信干噪比：

${{S}_{ki}}=\frac{U_{ki}^{H}{{H}_{ii}}{{V}_{ki}}V_{ki}^{H}H_{kk}^{H}{{U}_{ki}}}{U_{ki}^{H}{{B}_{ki}}{{U}_{ki}}}\frac{P\left( j \right)}{d\left( j \right)}$ (5)
其中噪声加干扰的协方差矩阵Bki为
$\begin{align} & {{B}_{ki}}=\sum\limits_{j=i}^{K}{\frac{P\left( j \right)}{d\left( j \right)}}\sum\limits_{d=1}^{d\left( j \right)}{{{H}_{ki}}{{V}_{dj}}V_{dj}^{H}H_{ki}^{H}-} \\ & \frac{P\left( i \right)}{d\left( i \right)}{{H}_{ii}}{{V}_{ki}}V_{ki}^{H}H_{ii}^{H}+{{I}_{Nr}} \\ \end{align}$ (16)
因此，最大信干噪比准则下的第i个接收端的第k个数据流的干扰抑制矩阵为
${{U}_{ki}}=\frac{{{\left( {{B}_{ki}} \right)}^{-1}}{{H}_{ii}}{{V}_{ki}}}{\left\| {{\left( {{B}_{ki}} \right)}^{-1}}{{H}_{ii}}{{V}_{ki}} \right\|}$ (17)

利用信道的互惠性，则最大信干噪比(max_SINR)算法流程如下.

1) 随机初始化预编码矩阵Vj.

2) 开始迭代. 根据式(16)计算接收端i的第k个数据流的噪声加干扰的协方差矩阵Bki，其中1≤i≤K,1≤k≤d(i).

3) 根据式(17)计算接收端i的第k个数据流的干扰抑制矩阵Uki，1≤i≤K,1≤k≤d(i).

4) 逆向通信，此时令$\overleftarrow {{V_i}} = {U_i}$.

5) 计算逆向接收端i的第k个数据流的噪声加干扰的协方差矩阵${\overleftarrow B _{ki}}$，1≤i≤K，1≤k≤d(i).

6) 计算接收端i的第k个数据流的干扰抑制矩阵${\overleftarrow U _{ki}}$.

7) 反转通信，令Vi=${\overleftarrow U _i}$.

8) 迭代直到收敛.

3 性能仿真及结果

下面给出提出算法与天线干扰消除方法[3]、射频干扰消除方法[4]的性能比较. 针对多用户全双工通信，仿真K=2用户全双工干扰信道，天线配置M=2，即发送天线数Nt和接收天线数Nr均为2，所有信道都是独立同分布瑞利信道，信道矩阵服从均值为0，方差为1的复高斯分布；每个发送端只向其对应的接收端发送期望信号，接收端接收到其他发送端的信号都视为干扰. 仿真结果如图 3所示.

图3 不同信噪比下干扰泄漏功率与算法迭代次数关系(K=2和M=2)

为了验证提出算法的有效性和正确性. 图 3给出了不同信噪比(SNR为5 dB和SNR为20 dB)下，干扰泄漏功率与算法迭代次数关系. 从图 3可以看出，随着迭代次数增加干扰泄漏功率逐渐减小. 在低信噪比(SNR为5 dB)情况下，min_IL算法和max_SINR算法大约750次迭代之后，干扰泄漏总功率小于10-5 W；在高信噪比(SNR为20 dB)情况下，min_IL算法大约500次迭代之后干扰泄漏总功率小于10-5 W，max_SINR算法大约300次迭代之后，干扰泄漏总功率小于10-5 W. 图 3结果表明，不论是在低信噪比还是高信噪比下，采用提出的算法后干扰泄露功率随着迭代次数增加不断减少，从而保证了算法的正确性，并在不同信噪比下验证了算法的有效性.

图 4为不同算法下系统容量随SNR变化的对比曲线. 可以看出，无论哪种用户数和天线配置，容量随着信噪比的增加而增加. 提出算法在容量上比文献[3]中的天线干扰消除方法、文献[4]中的射频干扰消除方法都有较大提高. 此外，在性能方面最大信干噪比算法优于最小干扰泄漏算法，但这也充分验证了对于最小干扰泄漏算法，但由于并没有考虑期望信号的路径，在性能上会低于最大信干噪比算法.

图4 不同算法的容量随SNR变化的对比曲线(K=2和M=2)

在对不同算法的平均能量效率进行仿真时，定义平均能量效率的单位为每焦耳所传输的比特数，计算公式为：η=1b(1+S/N)/Eb，其中：S为信号功率，N为噪声功率，Eb为单位比特能量. 从图 5的仿真结果可以看出，在平均能量效率上提出本文算法比文献[3]中的天线干扰消除方法、文献[4]中的射频干扰消除方法均有所提高，并且依然是最大信干噪比方法优于最小干扰泄漏，尤其是在小信噪比的情况下尤为明显，随着信噪比的增大影响明显减小.

图5 不同算法的平均能量效率对比曲线(K=2和M=2)

为进一步证明提出算法的优越性，考虑残留干扰加噪声功率对系统的影响，图 6为不同天线数下系统所受干扰加噪声功率比较. 图 6结果表明，无论哪种用户和天线数的配置，采用提出算法后，系统所受的干扰加噪声的影响明显减小，即进一步证明了提出算法的干扰消除性能要优于文献[3]的天线干扰消除方法和文献[4]的射频干扰消除方法.

图6 不同天线数下系统所受干扰加噪声功率比较
4 结束语

将干扰对齐思想应用于多用户全双工干扰信道的自干扰和互干扰消除是一种新思路. 首先是分析多用户全双工干扰信道并给出等效模型，然后基于全双工信道的互惠性，将信道和信号进行等效，再应用迭代干扰对齐的思想，采用最小干扰泄露和最大信干噪比方法来进行自干扰和互干扰消除，结果显示提出方案较其他方案有明显性能优势.

参考文献
[1] 尤肖虎, 潘志文, 高西奇. 5G通信发展趋势与若干关键技术[J]. 中国科学: 信息科学, 2014, 44(5): 551-563. You Xiaohu, Pan Zhiwen, Gao Xiqi. Developmental tendence and some key technologies of 5G communication [J]. China Science: Information Science, 2014, 44(5): 551-563.[引用本文:1]
[2] Sabharwal A, Schniter P, Guo Dongning, et al. In-band full-duplex wireless: challenges and opportunities [J]. IEEE Journal on Selected Areas in Communications, 2014, 32(9): 335-349.[引用本文:1]
[3] Jainy M, Choiy J, Kim T, et al. Practical, real-time, full duplex wireless [C]//Proceeding of ACM Annual International Conference on Mobile Computing and Networking (MobiCom). 2011(9): 19-23.[引用本文:5]
[4] Hua Yyingbo, Liang Ping, Ma Yiming, et al. A method for broadband full-duplex MIMO radio[J]. IEEE Signal Processing Letters, 2012, 19(12): 793-796.[引用本文:5]
[5] Duarte M, Dick C, Sabharwal A. Experiment-driven characterization of full-duplex wireless systems [J]. IEEE Transactions on Wireless Communications, 2012, 11(12): 4296-4307.[引用本文:1]
[6] Feng Daquan, Lu Lu, Wu Yiyuan, et al. Device-to-device communications in cellular networks [J]. IEEE Communications Magazine, 2014, 52(4): 49-55.[引用本文:1]
[7] 章扬, 周正, 石磊, 等. 基于严格势博弈的干扰对齐[J]. 北京邮电大学学报, 2013, 36(2): 51-54. Zhang Yang, Zhou Zheng, Shi Lei, et al. Interference alignment based on exact potential game[J]. Journal of Beijing University Posts and Telecommunication, 2013, 36(2): 51-54.[引用本文:1]
[8] Gomadam K, Cadambe V R, Jafar S A. A distributed numerical approach to interference alignment and applications to wireless interference networks[J]. IEEE Transactions on Information Theory, 2011, 57(6): 3309-3322.[引用本文:1]
基于干扰对齐的多用户全双工通信中干扰消除方法
谢显中, 王闯, 张森林, 葛振涛