引用本文
敬茂华, 江彬, 辛阳, 杨义先. PFA在FPGA正则引擎上的设计和仿真[J]. 北京邮电大学学报, 2015, 38(6): 69-73.  
JING Mao-hua, JIANG Bin, XIN Yang, YANG Yi-xian. Design and Simulation of FPGA Engine for Regular Expressions Matching Based on PFA[J]. JOURNAL OF BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS, 2015, 38(6): 69-73.  
Permissions
Copyright©2015, 《北京邮电大学学报》编辑部
《北京邮电大学学报》编辑部 所有
PFA在FPGA正则引擎上的设计和仿真
敬茂华1,2,3, 江彬2, 辛阳3,4, 杨义先2,4    
1. 东北大学秦皇岛分校 计算机与通信工程学院, 河北 秦皇岛 066004;
2. 东北大学 信息科学与工程学院, 沈阳 110819;
3. 云安全技术北京市工程实验室, 北京 100082;
4. 北京邮电大学 信息安全中心, 北京 100876
作者简介: 敬茂华(1977—),女,讲师,E-mail:jing_jmh@163.com;杨义先(1961—),男,教授,博士生导师.
收稿日期: 2015-01-22
基金项目: 国家自然科学基金项目(61100021,61121061,61202447);河北省自然科学基金项目(F2012501014);河北省教育厅自然科学指导项目(Z2010215)
摘要

将后缀自动机构造方法应用到现场可编程门阵列的正则引擎设计上,能够有效地压缩状态空间,提高"速度"和"面积"这2个最主要的现场可编程门阵列的引擎性能指标,并能利用有限的现场可编程门阵列资源来实现更多正则表达式的匹配处理. Testbench模拟仿真结果表明,所设计的正则引擎完全实现了预期匹配要求,而其支持的正则表达式的数量和匹配速度都因有效的规模压缩而得到了很大的提升,对比传统的基于Thompson不确定的有限自动机实现的硬件引擎,其所需要的硬件逻辑资源更少,能够并行执行的正则表达式数量也就越多,有效地提高了匹配效率.

关键词: 正则表达式    模式匹配    现场可编程门阵列    后缀自动机    Thompson不确定的有限自动机         
中图分类号: TN393 文献标志码:A 文章编号:1007-5321-38-6-69 DOI:10.13190/j.jbupt.2015.06.015
Design and Simulation of FPGA Engine for Regular Expressions Matching Based on PFA
JING Mao-hua1,2,3, JIANG Bin2, XIN Yang3,4, YANG Yi-xian2,4    
1. School of Computer and Communication Engineering and Northeastern University at Qinhuangdao, Hebei Qinhuangdao 066004, China;
2. College of Information Science and Engineering and Northeastern University, Shenyang 110819, China;
3. Beijing Engineering Laboratory for Cloud Security, Beijing 100082, China;
4. Information Security Center, Beijing University of Posts and Telecommunications, Beijing 100876, China
Abstract

A field programmable gate array(FPGA) engine for regular expressions matching based on postfix automata(PFA) was designed. PFA can obtain smaller size and then reduce the space effectively. The limited FPGA resources can be used to implement more regular expressions simultaneously. Simulation by Testbench implies that the number and speed of the supported regular expressions is deeply improved. Compared with Thompson non-deterministic finite automata (NFA) method, it needs less hardware resources and the number of regular expressions that can be implemented concurrently becomes more, so the efficiency of implement has been increased.

Key words: regular expression    pattern matching    field programmable    postfix automata    Thompson non-deterministic    

正则表达式在各个领域得到了广泛应用，但目前该技术面临着诸多挑战. 近年来硬件正则引擎设计成为一大研究热点，不确定的有限自动机(NFA，non-deterministic finite automata)的位并行特性非常适宜于现场可编程门阵列(FPGA，field programmable gate array)并行匹配模式. 现有FPGA引擎基本都是基于Thompson构造法，笔者采用后缀自动机(PFA，postfix automata)[1, 2]算法来实现FPGA引擎. Testbench模拟仿真结果表明，该算法能够完全实现预期匹配要求，获得很好的性能指标.

1 相关工作

正则匹配硬件结构研究始于1982年. 2001年，Sidhu等[3]首次提出从正则表达式到基于FPGA的NFA映射算法；Cho等[4]设计了将正则表达式转换成硬件电路的软件，用NFA动态生成高效电路；Bispo等[5]用可重构逻辑来实现NFA匹配，并设计了自动转换工具；2008年Badran等[6]实现了多字符输入NFA；2012年Yamagaki等[7]提出了状态合并NFA构造方法；2010年Korenek等[8]提出了一种节省FPGA资源的新架构.

2 PFA方法概述

FPGA正则引擎设计大体上分为2个步骤：1)构造NFA；2)根据NFA实现各个元符号所对应的FPGA逻辑电路. 用于构造正则表达式的NFA的算法很多，目前FPGA实现中通常采用Thompson算法. 笔者使用PFA构造算法来设计并实现FPGA正则引擎，包含预处理、构造正则解析树、构造正则后缀树、合并等价状态获得NFA这4个步骤，构造r=abx*cd+efy*gh的PFA实例如下. 其中“*”为闭包运算.

预处理，得

r′=abx*cdεefy*gh+

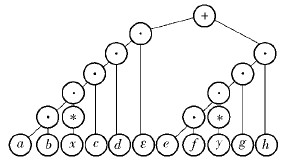
构造正则解析树，如图 1所示.

图1 正则表达式r=abx*cd+efy*gh的解析树

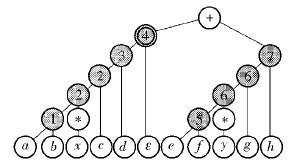
状态合并编码如图 2所示. 构造NFA如图 3所示.

图2 基于解析树的状态合并编码

图3 正则表达式r=abx*cd+efy*gh的NFA

1) PFA构造算法复杂度分析

空间复杂度：PFA算法需要存储和维护1棵二叉树，其节点最小为n+k，最大为n+k+2. 其中，n为输入符号个数，k为运算符个数. 因此，空间复杂度与正则表达式组的长度线性相关，为O(n).

时间复杂度：PFA构造算法全都是基于二叉树遍历操作来实现的，复杂度为O(n)，基于二叉树遍历操作获得状态空间和弧转换关系，复杂度为O(n). 获取当前状态节点的左叶子节点标记符号和更新当前逻辑前驱状态的操作复杂度为O(1). 获取左叶子节点、右叶子节点，以及处理路径上是否有闭包运算(*)节点的操作，需要对21b(n+1)-1个叶子节点进行创建弧操作，复杂度为O(n). 综上，复杂度为O(n2).

2) 规模压缩效率分析

PFA状态数最多为k+2，状态转换弧的条数最多为n+i，0≤i«j，j为正则表达式中闭包运算的个数. 因此，PFA的规模在最好的情况下为s=n+k+i+2≈2n+2，即为O(2n)；在最坏的情况下为s=n+k+i+2≈3n+2，即为O(3n)；通常情况下i=0,1，所以PFA的规模在平均情况下为O(2n). Thompson NFA规模通常不低于O(6n).

3 FPGA设计 3.1 设计思想

通过对Snort系统的正则表达式的语法进行分析，将扩展正则表达式中的各种符号按照其特点和形式进行分类，设计出固定的通用子模块. 对纯正则表达式采用PFA算法构造其规模更小的NFA，然后通过将已经设计好的固定通用子模块进行组合，从而实现整个正则表达式的模式匹配硬件逻辑. 在PFA的构造上，笔者采用Handle C实现了PFA算法，然后将PFA算法的C程序转换成Verilog HDL程序，该程序接收动态输入的纯正则表达式并构造其等价的NFA.

3.2 通用子模块的设计

1) 字符比较模块

这是最基本也是最常用的模块. 采用Verilog HDL语言编程实现，如图 4所示.

图4 字符比较模块

2) 重复匹配模块

重复匹配有以下3种情况：a.匹配次数为n次，表示为{n}；b.匹配次数大于n次，表示为{n,}；c.匹配次数大于n次小于m次，表示为{n,m}. 根据3种不同的情况分别编程并生成相应的子模块供后续电路调用.

① 匹配n次的模块{n}，如图 5所示.

图5 重复匹配次数为n次的模块

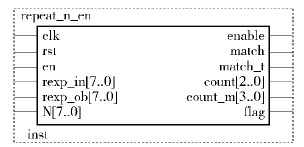
② 重复匹配大于n次的模块{n,}，如图 6所示.

图6 重复匹配次数大于n次的模块

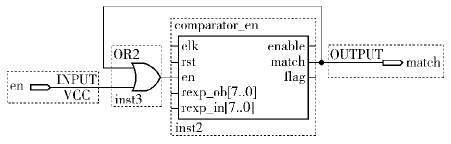
③ n＜匹配次数＜m次的模块{n,m}，如图 7所示.

图7 重复匹配次数大于n次小于m次的模块

3) 任意字符匹配，如图 8所示.

图8 任意字符匹配模块

4) 范围约束匹配

① 字符集合匹配模块[abc]，如图 9所示.

图9 字符集合匹配模块

② 反集合匹配模块[abc]，如图 10所示.

图10 反集合匹配模块

③ 范围匹配模块[a～z]，如图 11所示.

图11 范围匹配模块

④ 反范围匹配模块[^a～z]，如图 12所示.

图12 反范围匹配模块

5) 其他字符匹配模块

① 问号元字符r?，如图 13所示.

图13 问号元字符r?

② 加号元字符r+，如图 14所示.

图14 加号元字符r+

③ 星号元字符r*，如图 15所示.

图15 星号元字符r*

④ 分支元字符r1|r2，如图 16所示.

图16 分支元字符r1|r2

以上各例均通过测试代码的仿真验证，结果与正则表达式所要表达的功能完全一致.

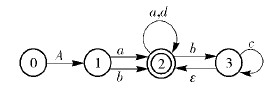
4 PFA的实现仿真及性能分析

下面给出典型实例r=A(a|b)(a*|bc*|d*)*的PFA与Thompson NFA的性能分析比较.

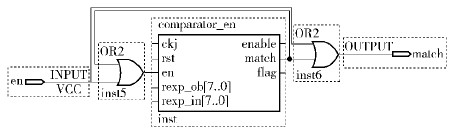
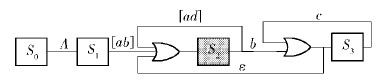
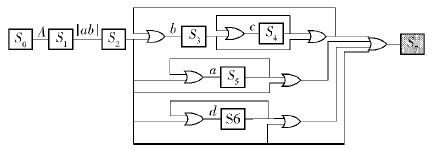
对如图 17所示的PFA进行逻辑化处理，得逻辑电路基本构造，如图 18所示.

图17 r=A(a|b)(a*|bc*|d*)*的PFA

图18 NFA的逻辑实现

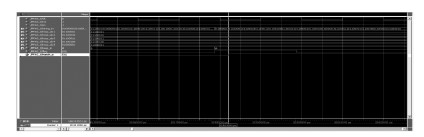
利用Testbench进行模拟仿真，结果与预期完全一致，如图 19所示，延时为2 320 ps.

图19 仿真波形放大显示图

r=A(a|b)(a*|bc*|d*)*的Thompson NFA如图 20所示.

图20 r=A(a|b)(a*|bc*|d*)*的Thompson NFA

优化后得其逻辑电路，如图 21所示.

图21 NFA的逻辑实现

在Testbench平台上对以上程序进行测试仿真，仿真结果如图 22所示，延时时间差为2 824 ps.

图22 仿真波形与放大显示图

从表1可知，PFA自动机构造法在匹配速度上比Thompson构造法快0.32%左右，而在消耗逻辑元件和寄存器等资源方面均比Thompson要少.

表1 性能、资源数比较

为了验证基于PFA的FPGA方案在匹配效率上的提升，任选构造的20组结构或复杂度不同的正则表达式来进行仿真对比. 仿真实验分别通过PFA和Thompson算法进行系列变换，最后用FPGA实现对应的匹配电路，通过建立Testbench测试平台，在Modelsim上进行时序仿真，得到的延时特性数据如图 23所示，其中匹配时钟为160 ns.

图23 PFA与Thompson算法性能比较
5 结束语

PFA方法能够以O(n2)的时间复杂度和O(n)的空间复杂度获得规模最小的NFA和寄存器转换级(RTL，register transfer level)仿真结果，在FPGA上采用PFA能够以更少的逻辑资源实现正则表达式匹配. 后续考虑扩展PFA方法到Snort和Perl等工具和语言的正则表达式技术中，基于实际需求和正则表达式库中的分组处理模式，切实有效地解决由于实际系统中正则表达式数量激增带来的效率低下问题.

参考文献
[1] Jing Maohua, Yang Yixian, Lu Ning, et al. Postfix automata[J]. Theoretical Computer Science, 2015(562): 590-605.[引用本文:1]
[2] 敬茂华, 杨义先, 汪韬, 等. 新颖的正则NFA引擎构造方法[J]. 通信学报, 2014(10): 98-106. Jing Maohua, Yang Yixian, Wang Tao, et al. Novel NFA engine construction method of regular expressions[J]. Journal on Communications, 2014(10): 98-106.[引用本文:1]
[3] Sidhu R, Prasanna V K. Fast regular expression matching using FPGAs[C]//Field-Programmable Custom Computing Machines, FCCM 2001. France: IEEE Press, 2001: 227-238.[引用本文:1]
[4] Cho Y H, Navab S, Mangione-Smith W H. Specialized hardware for deep network packet filtering[C]//Field-Programmable Logic and Applications: Reconfigurable Computing is Going Mainstream. [S. l. ]: Springer Berlin Heidelberg, 2002: 452-461.[引用本文:1]
[5] Bispo J, Sourdis I, Cardoso J M P, et al. Regular expression matching for reconfigurable packet inspection[C]//Field Programmable Technology, FPT 2006. IEEE International Conference on Field Programmable Technology. Bangkok: IEEE Press, 2006: 119-126.[引用本文:1]
[6] Badran T F, Ahmad H H, Abdelgawad M. A reconfigurable multi-byte regular-expression matching architecture for signature-based intrusion detection[C]//Information and Communication Technologies: from Theory to Applications, ICTTA 2008. Piscataway: IEEE Press, 2008: 1-4.[引用本文:1]
[7] Yamagaki N, Sidhu R, Kamiya S. High-speed regular expression matching engine using multi-character NFA[C] //Field Programmable Logic and Applications, FPL 2008.Heidelberg: IEEE Press, 2008: 131-136.[引用本文:1]
[8] Korenek J, Kosar V. Efficient mapping of nondeterministic automata to FPGA for fast regular expression matching[C]//Design and Diagnostics of Electronic Circuits and Systems, DDECS 2010. Piscataway: IEEE Press, 2010: 54-59.[引用本文:1]