2. 河南大学 软件学院, 河南 开封 475000;
3. 北京信息科技大学 计算机学院, 北京 100101
为了解决Hadoop分布式文件系统(HDFS)平台上小文件的存在带来MapReduce程序运行能耗成本偏高问题,建立Hadoop节点集群的能耗模型进行分析推导,证明了在Hadoop平台上,存在能使程序运行能耗成本最低的最优文件大小,并在此基础上结合经济学边际分析理论提出一种基于能耗成本和访问成本考虑的最优文件大小判定策略. 此策略可以对存放在HDFS上的小文件合并进行效益计算,将小文件合并为成本最优文件大小以获得最佳收益. 通过实验证明了能效最优数据块大小的存在,并通过实验证明了成本和效益相结合利用边际分析理论来确定数据块大小的合理性和有效性.
2. Software School, Henan University, Henan Kaifeng 475000, China;
3. Computer School, Beijing Information Science and Technology University, Bejing 100101, China
The map reduce program operated on Hadoop distributed file system (HDFS) has a high-energy-cost problem caused by existence of small files. In order to solve this problem, the article established a new energy model of Hadoop node cluster to analyze data then proved that there exists the optimal file size on Hadoop which can reduce the energy cost of program operation to the lowest level, and based on the above data and the margin analysis theory, a judging strategy was put forward, which can find the optimal file size from the angle of energy cost and visit cost. This strategy can merge the small files on HDFS to the optimal file size according to the cost efficiency, so to get the best benefit. The existence of optimal sized data block was proved by examination, and the reasonability and validity of identifying the data block size by the combination of cost and efficiency under the margin analysis theory are proved as well by examination.
Jim Gray提出一个经验性定律,在网络环境下每18个月产生的数据量等于有史以来数据量总和. 大量数据带来的是存储的成倍增长,进而存储能耗不断增长. 大规模数据中心存储能耗比例占整个数据中心能耗的27%~40%. HDFS是一种具有代表性的云存储,它是Hadoop分布式文件系统(HDFS,Hadoop distributed file system)平台的文件系统,适用于大规模数据集,但对小文件的处理效率不高[1],笔者研究的是HDFS小文件合并后的成本效益问题.
1 相关研究由于小文件的存在以及MapReduce本身架构的制约,HDFS对小文件处理效率不高,这引起了很多学者的关注. Dong[1]等所提出小文件处理的方法主要是针对PPT文件存储效率的提高,Zhang[2]等针对社交网站SNS(social networking sites),提出了一种存储机制来提高存储效率,但这些对小文件合并研究集中在特定文件存取效率方面,对系统能耗成本并未考虑. 当前也有一些文章是研究HDFS能效问题的,有些是从关闭节点[3]考虑的,有些是通过调度算法[4, 5]节能的,这些研究均没有从文件大小和能效之间的关系来考虑. 本研究重点是在物理资源一定的情况下,HDFS存放一定规模文件,文件大小对Hadoop系统程序运行的能耗影响.
2 能效成本分析 2.1 问题描述在HDFS上,小文件一般是指低于64 MB大小的文件. HDFS是用Namenode来管理文件系统中的文件,大量的小文件占用了Namenode的资源,降低程序运行的效率,提高了程序运行时CPU利用率,进而导致程序运行时系统能耗的增加. 对于经常执行统计或分析程序的HDFS文件系统而言,程序执行带来的能耗影响不可忽视.
对于一个由n个节点组成的Hadoop集群,根据物理学能耗公式$E = \int {P\left( t \right){\rm{d}}t} $,可得该集群能耗
| $ {E_{\left[ {{t_1},{t_2}} \right]}} = \sum\limits_{i = 1}^n {\int_{{t_1}}^{{t_2}} {{P_i}\left( t \right){\rm{d}}t} } $ | (1) |
而对于其中的一个节点,根据FAN模型[6],节点功率P可以表示为
| $ {P_{{\rm{pred}}}} = {C_0} + {C_1}{U_{{\rm{cpu}}}} $ | (2) |
其中:C0为常数,是服务器在空闲状态时的功率;C1为服务器峰值状态功率和空闲状态功率的差值. 用时间片占用率来计算CPU占用率也是常用的方法,用ω表示CPU每秒钟执行的平均任务量,δ表示CPU每秒基准计算能力. 时间片计算CPU利用率一般这样表达:CPU占用率 = 1个周期内任务的总运行时间/1个周期内的总时间,若1个时间周期是1 s,1个周期内该任务运行的总时间为t,该CPU每秒的运算能力为λ,则上述表达可以推导$\frac{t}{1} = \frac{{t\lambda }}{\lambda }$,tλ就是这1 s所完成的任务量,即ω,而λ就是该CPU在1 s的基准计算能力,即δ,则可得CPU的利用率
| $ {U_{{\rm{cpu}}}} = \frac{\omega }{\delta } $ | (3) |
其中:ω为CPU每秒钟执行的平均任务量,δ为CPU每秒基准计算能力. 服务器的计算能力在硬件不变的情况下是固定的,而计算任务可用式(4)来表达:
| $ \omega = {\omega _{{\rm{work}}}} + {\omega _{{\rm{operate}}}} $ | (4) |
其中:ωwork为每秒执行的工作计算量,这个计算量的降低只能依靠算法的改进;ωoperate为对任务进行操作和控制每秒所消耗的计算量,是计算框架消耗的计算量. 一般来说,HDFS对应的计算平台是Hadoop平台,则ωoperate主要是由MapReduce这个计算框架消耗. 根据MapReduce的运行机制,可以得出每建立一个任务,就会占用系统一部分资源,如果task过多,则会占用太多资源,如果太少,则影响系统的并行度,影响计算速度. 对于一个节点i来讲,它的能耗为
| $ E = PT = \left( {{C_0} + {C_1}{U_{{\rm{cpu}}}}} \right){T_i} $ | (5) |
在实际运行过程中,只要服务器开启,C0就是存在的,是一个常数,所以引起能耗变化的主要是CPU的波动,定义其为ΔE. 则
| $ \Delta E = {C_1}{U_{{\rm{cpu}}}}{T_i} $ | (6) |
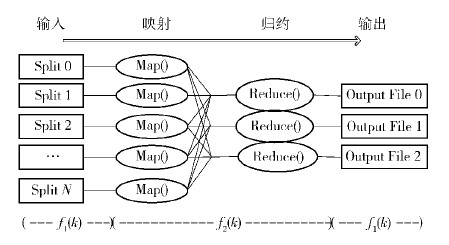
上文已经分析了在不改变算法的情况下,在Hadoop系统中,影响功率变化的因素,而影响时间T的因素又有哪些? 把集群对工作的处理时间描述为以小文件数k为变量的函数. I/O时间f1(k),并行处理时间f2(k),I/O时间f1(k)分为读取时间和输出时间,这个时间和读取的文件大小以及寻址时间有关,f2(k)是并行处理时间,如图 1所示.
在图 1中,I/O时间如f1(k)所示,指的是数据读取时间和数据输出时间. 并行处理时间,是指执行Map和Reduce进行程序运行时间,即f2(k). 如图 1所示,f1(k)时间内,各节点并行读取数据,但是不相互依赖,因此
| $ {f_1}\left( k \right) = \frac{D}{{nv}} = \frac{D}{{n\varphi \left( {k/n} \right)}} $ | (7) |
其中:D(MB)为要读取的数据量,n为存放数据的节点数目,v为节点读取速度,单节点读取速度可以用函数φ(k/n)表示,k为小文件数目. 对于单个节点,其小文件越多(即k/n越大),数据的读取速度越低,v越小,这时f1(k)也就越大.
| $ {f_2}\left( k \right) = \frac{{{R_{{\rm{tasks}}}}}}{{n\left( {k/n} \right){R_k}}}{\omega _h}\left( k \right) = \frac{{{R_{{\rm{tasks}}}}}}{{k{R_k}}}{\omega _h}\left( k \right) $ | (8) |
其中:Rtasks为总的工作计算量(不包含计算框架的计算量),n为节点数目,当MapReduce中的作业调度器调度作业时,会为每个数据块建立一个Map,并将Map任务分配给TaskTracker执行. 由于HDFS数据副本放置的均衡特性,一般认为文件分布是均匀的,则Rtasks/n是每个节点分摊的计算任务量;Rk为系统中启动的每个Map每秒所能获得的计算资源,那么,每个节点所能为工作提供的计算资源就是(k/n)Rk;函数ωh(k)为并行依赖度,k越大,则计算过程并行依赖度越强. 对于(k/n)Rk来说,有
| $ 0 \le \left( {k/n} \right){R_k} < {R_{{\rm{total}}}} - {R_{{\rm{operate}}}} $ | (9) |
其中:Rtotal为该节点每秒的计算资源总量,Roperare为系统和MapReduce控制任务运行每秒所消耗的资源量. Roperare可以用一个函数θ(k)来表示,该函数是k的增函数,也就是k值越大,θ(k)越大. (Rtotal-θ(k))表示可以用于计算任务的资源,k越大,可用的计算资源也就越小.
通过式(9)可以分析,对于单个节点,当k低于一定阈值时,(k/n)Rk随着k增大而增大,可用(k/n)Rk来表示该节点为执行工作而分得的计算资源量,当k超出一定的阈值(这时CPU资源完全被计算任务和计算框架占据),该节点用来执行工作分得的计算资源量应描述为Rtotal-θ(k),随着k的增加而不断减少,假设此阈值为ε. 综合式(7)和式(8),可得
| $ \begin{array}{*{20}{c}} {T = f\left( k \right) = {f_1}\left( k \right) + {f_2}\left( k \right) = }\\ {\left. {\begin{array}{*{20}{c}} {\frac{D}{{n\varphi \left( {k/n} \right)}} + \frac{{{R_{{\rm{tasks}}}}}}{{k{R_k}}}{\omega _h}\left( k \right),\;\;\;k \le \varepsilon }\\ {\frac{D}{{n\varphi \left( {k/n} \right)}} + \frac{{{R_{{\rm{tasks}}}}}}{{n\left( {{R_{{\rm{total}}}} - \theta \left( k \right)} \right)}}{\omega _h}\left( k \right),\;\;\;k > \varepsilon } \end{array}} \right\}} \end{array} $ | (10) |
已知Hadoop集群有n个节点,总量为D的小文件,存放在HDFS文件系统中(HDFS默认block为64 MB),k=D/Sdata(Sdata为合并后文件大小),对这些数据运行统计程序A,其能耗关系满足式(3)(5)(6),时间关系满足式(10),证明存在一个k值使得集群运行程序A能效最优,即ΔE最小.
证明 对于整个集群,$\Delta {E_{{\rm{total}}}} = \sum\limits_{i = 0}^n {\Delta {E_i}} $
对于节点1,由式(3)可得
| $ {U_{{\rm{lcpu}}}} = \frac{{{\omega _1}}}{{{\delta _1}}} = \frac{{{\omega _{1{\rm{work}}}} + {\omega _{1{\rm{operate}}}}}}{{{\delta _1}}} $ |
当k>ε1(ε1即对应式(10)所描述的阈值ε)
| $ \begin{array}{*{20}{c}} {\Delta {E_1} = {P_1}{T_1} = }\\ {\left( {\frac{{{\omega _{1{\rm{work}}}} + {\omega _{1{\rm{operate}}}}}}{{{\delta _1}}}} \right){T_1} = \frac{{{\omega _{1{\rm{work}}}}{T_1}}}{{{\delta _1}}} + \frac{{{\omega _{1{\rm{operate}}}}{T_1}}}{{{\delta _1}}} = }\\ {\left( {\frac{{{R_{1{\rm{tasks}}}}}}{{{\delta _1}}} + \frac{{{\omega _{1{\rm{operate}}}}}}{{{\delta _1}}}} \right)\left( {\frac{D}{{n{\varphi _1}\left( {k/n} \right)}} + } \right.}\\ {\left. {\frac{{{R_{1{\rm{tasks}}}}}}{{n\left( {{R_{1{\rm{total}}}} - {\theta _1}\left( k \right)} \right)}}{\omega _h}\left( k \right)} \right)} \end{array} $ |
由于R1tasks/δ1是一个常量(在没有节点出现故障的情况下,执行同一个程序,每个节点所得任务量变化很小),ω1operate,φ-11(k/n),(R1total-θ1(k))-1,ωh(k)均是(ε1,+∞)区间上的递增函数(见式(7)~(9)的推导),又因为k是正整数,所以在区间(ε1,+∞),当k=ε1+1时,ΔE最小.
同理,对于节点2,3,…,n,分别存在{(ε2+1),(ε3+1),…,(εn+1)},分别在(ε2,+∞),(ε3,+∞),…,(εn,+∞)区间上递增;
由于{(ε2+1),(ε3+1),…,(εn+1)}是由n-1个正整数组成的有限集;
所以存在一个正整数ψ,使得
ψ=max{(ε2+1),(ε3+1),…,(εn+1)}
若ε′为正整数,可设ε′+1=ψ.
1) 当k>ε′;ΔEtotal在(ε′,+∞)上递增,当k=ε′+1时,ΔEtotal最小;
2) 当k≤ε′;对于ΔEtotal来说,由于[1,ε′]是一个闭合区间,且k只能取整数,那么[1,ε′]是一个整数有限集;则必然存在k=m使得ΔEtotal在[1,ε′]有最小值;
综合1)和2),min{ΔEtotal(ε′),ΔEtotal(m)}为ΔE的最小值;所以,存在且必然存在一个整数k使得ΔE有最小值,证毕.
3 基于边际分析的文件合并策略文件的作用不仅是提供程序运行数据,还有访问功能. 这就引发了一个问题,合并后的文件越大,文件内部索引就越复杂,访问到某个数据的定位成本越高. 这样,进行小文件合并就带来了双向问题,收益是节能的能耗收益,成本则来源于访问和进行索引定位的成本,当对小文件的访问达到一定频率时,合并就变得无意义. 为了解决这个问题,采用了经济学的边际分析理论. 合并小文件的边际成本可定义为
| $ J = {m_{\rm{v}}}f\left( s \right){p_{\rm{v}}} $ | (11) |
其中:mv为每小时文件的访问次数,f(s)为大小为s的文件单次访问的成本函数,pv为单次访问的成本价格.
合并小文件的效益可以定义为
| $ B = {m_{\rm{e}}}\Delta E{p_{\rm{e}}} $ | (12) |
其中:me为每小时程序运行的次数,ΔE为运行程序节约的能耗,pe为获得的能耗收益价格,s2为合并后文件大小,那么
| $ \begin{array}{*{20}{c}} {\Delta J = {m_{\rm{v}}}\left( {f\left( {{s_2}} \right) - f\left( s \right)} \right){p_{\rm{v}}}}\\ {\Delta B = {m_{\rm{e}}}\left( {\Delta {E_{{s_2}}} - \Delta {E_s}} \right){p_{\rm{e}}}} \end{array} $ |
根据边际分析理论,当边际成本的变化率和边际收益的变化率相等时,Hadoop系统的总收益达到最大,即
| $ \frac{{\Delta B}}{{\Delta J}} = \frac{{{m_{\rm{e}}}\left( {\Delta {E_{{s_2}}} - \Delta {E_s}} \right){p_{\rm{e}}}}}{{{m_{\rm{v}}}\left( {f\left( {{s_2}} \right) - f\left( s \right)} \right){p_{\rm{v}}}}} = 1 $ |
pv和pe分别为访问成本价格和能耗价格,将它们统一换算为价格便可以求解. 定义mv=1 000,me=2,定义price的基本单位为H(毫),1分=10 H,也就是把检索成本和能耗成本换算成货币. 对J和B都通过s的变化规律拟合了一个线性函数,以此来求解.
用边际效益理论求解最优文件成本时,可用5 MB或者10 MB为一个增量进行递增求解. 从表 2可以看到文件大小从5 MB增加至10 MB,程序运行有明显收益0.008 kW·h,从10 MB增至20 MB时收益只有0.001 kW·h. 递增变量设置小于5 MB时,只有在文件大小低于10 MB的时候收益变化明显,而检索成本相对平缓,所以求解时将增量定为5 MB或10 MB较合适.
| 表2 合并后各种大小文件执行WordCount对应的时间和能耗 |
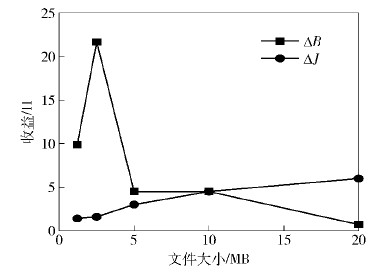
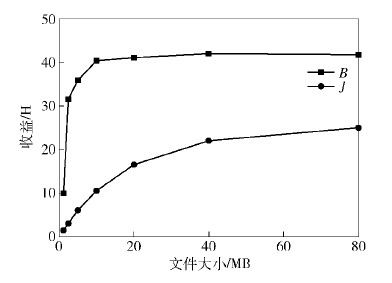
图 2和图 3所示是对大小低于1 MB,总计200 MB数据进行合并的实验. 用上文方法求得s为10 MB时系统收益最大. 图 2是合并小文件带来ΔB,ΔJ 变化,可看到文件合并到10 M时,ΔB/ΔJ≈1,此时收益最大. 通过图 3可以看出,当文件大小为10 MB,成本和收益的差值最大,也就证实对这200 MB的小文件,将其合并为每个10 MB的文件时收益最大.
4 实验
本实验的实验环境为Hadoop2.2.0,5台异构PC,其中1台作为Master节点,剩余4台作为Slave节点,测试数据为600~700 KB的英文文章,总数据量为200 MB,运行的程序为基准测试程序中的WordCount,机器编号和基本配置信息如表 1所示.
| 表1 Hadoop集群各节点基本信息表 |
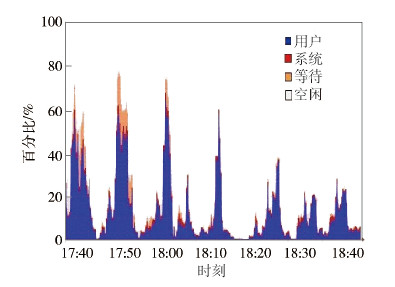
图 4所示是合并后文件大小分别为2.5、5、10、20、40、80、160 MB时,Hadoop集群执行WordCount程序对应的Hadoop集群CPU利用率变化情况. 从图 4可以看出,当文件较小时,运行WordCount程序计算量比较大,CPU利用率比较高,计算速度也比较低,并随着文件增大,CPU利用率和ΔE变化会趋于平缓.
表 2所示为在上述文件大小时,运行WordCount程序的时间以及所消耗的电能. 可以看出,在文件大小为40 MB时,可以获得WordCount程序近似最低能耗,这也证明了所提观点,即存在一个文件大小可以使得程序运行能效最优.
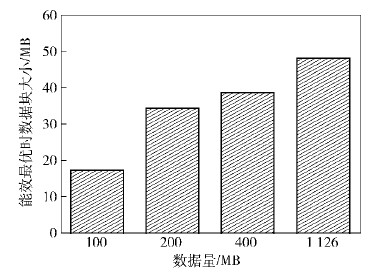
图 5所示为在此实验环境下不同数据规模的最优文件大小. 可以看出,最优文件大小随文件规模变化而变化. 从这个角度推导,无论何种规模的数据,都可以通过合并文件或者修改HDFS默认的Block大小来提高能效. 当文件过大时,调高Block,使Split对应更大数据块以获得合适的Map数;当文件过小时,合并文件使Split对应更多的文件获得合适的Map数,通过这些方式可达到能效优化的目标.
5 结束语在现有的Hadoop系统中,小文件的存在使得平台的实际使用效率降低,通过推导证明了存在一个最优文件大小使得执行程序能耗最低. 并通过实验验证了最优能效文件大小的正确性以及边际分析理论在小文件合并中成本效益分析中的有效性. 未来应进一步研究Hadoop系统中,如何建立更有效的索引提高小文件的存储效率,优化资源配置,提高Hadoop平台在程序运行时的能效.
| [1] | Dong Bo, Qiu Jie, Zheng Qinghua, et al. A novel approach to improving the efficiency of storing and accessing small files on Hadoop: a case study by PowerPoint files[C]//2010 IEEE International Conference on Services Computing IEEE Computer Society. Washington DC: IEEE Computer Society Press, 2010: 65-72.[引用本文:2] |
| [2] | Zhang Ganggang, Zuo Min, Liu Xinliang, et al. Improving the efficiency of storing SNS small files in HDFS[M]. Berlin: Springer Berlin Heidelberg Press, 2013: 154-160.[引用本文:1] |
| [3] | Liao Bin, Yu Jiong, Zhang Tao, et al. Energy-efficient algorithms for distributed storage system based on block storage structure reconfiguration [J]. Journal of Network & Computer Applications, 2015, 48(2): 71-86.[引用本文:1] |
| [4] | Bampis E, Chau V, Letsios D, et al. Energy efficient scheduling of MapReduce jobs[J]. Lecture Notes in Computer Science, 2014, 8632(8): 198-209.[引用本文:1] |
| [5] | Mashayekhy L, Nejad M M, Grosu D, et al. Energy-aware scheduling of MapReduce jobs for big data applications [J]. IEEE Transactions on Parallel & Distributed Systems, 2015, 26(1): 1.[引用本文:1] |
| [6] | Fan X, Weber W D, Barroso L A. Power provisioning for a warehouse-sized computer [J]. ACM SIGARCH Computer Architecture News, 2007, 35(2): 13-23.[引用本文:1] |