2. 总参信息化部驻成都地区军事代表室, 成都 610041
为分析和发现故障预测中表征网络运行状态的多指标和故障间的关联关系,提出了一种基于模糊神经网络的规则发现方法. 该方法利用模糊神经网络具有的学习能力和模糊推理能力,分析和发现网管系统中多指标和故障的关联关系,实现基于多指标的在线故障预测. 仿真实验结果表明,有效的参数初始化确定了算法收敛方向,从而加速了收敛速度;新方法能够准确预测故障的发生,并且优化了预测准确度、真正率、误判率等性能指标.
2. Military Representative Office in Chengdu of Information Department of PLA, Chengdu 610041, China
Aiming at analysis on correlations between failures and various indices characterizing network states in failure prediction, an approach for rule discovery based on fuzzy neural network (ARD_FNN) was proposed. It discoveries the correlations in network management system using the abilities to learn and infer by fuzzy logic in FNN. Simulations show that the effective initialization of parameters indicates the convergence directions that accelerate the convergence rates; thus the approach can predict the occurrence of failures accurately and such performance indicators as precision, true positive rate and false positive rate are optimized.
为了有效应对复杂的网络环境,实现故障的自主化管理,故障预测要求在故障发生前并且没有影响系统提供服务的前提下,利用网络的历史行为建模、预测即将发生故障的可能性. 故障预测系统要具有高度准确的预测能力和快速灵活的响应能力[1, 2, 3].
笔者基于网络管理系统采集的各类表征网络系统运行状态的指标数据,利用模糊神经网络(FNN,fuzzy neural network)所具有的学习能力和模糊推理能力[4],提出了一种规则发现方法,分析和发现了指标与故障触发的关联关系. 通过分析多指标和故障触发的时序关系、指标映射关系指导模型的参数初始化以及模型的训练优化,实现基于该模型的在线故障预测. 仿真实验结果表明,所提出的模型及方法优化了故障预测性能且算法较传统FNN具有更快的收敛速度.
1 模型描述 1.1 在线故障预测场景在线故障预测时序图如图 1所示. τ是进行故障预测的时间窗;Δtl是预测执行时间,实现在t时刻预测t+Δtl之后是否会发生故障;Δtw是Δtl的最小值,与执行某些主动式管理动作所需时间相关;Δtp是预测持续的时间. 因而,故障预测中,若在时刻t执行故障预测,即基于预测模型以及当前τ内获得的指标信息,预测在(t+Δtl,t+Δtl+Δtp)是否会发生故障[4].
“故障”是指由硬件缺陷、设计错误、不可靠环境或操作异常引起的服务或网络节点不可用. 笔者在进行故障关联规则发现以及故障预测时,并不对故障进行具体分类.
1.2 基于FNN的规则发现模型基于FNN的规则发现(ARD_FNN,approach for rule discovery based on FNN)模型由以下5层神经元节点组成.
1) 输入层
输入数值为可表征网络运行状态的τ个时隙内的指标,因而本层节点个数为τ. 设网管系统中采集的可用于故障预测的指标类别数为n,则输入层中输入的是τ个n维指标数据:X=(X1,X2,…,Xτ)T,其中Xk=(x1,x2,…,xn).
2) 预处理层
上报的指标分为3类:正常N、告警A、故障F. 其中,告警还可细化为严重告警Acritical、主要告警Amajor 、次要告警Aminor、警告Awarning 4个等级. 因而指标对应6个不同状态:S={N,Awarning,Aminor,Amajor,Acritical,F}.
针对输入的τ个n维指标数据,预处理层对应了τ×n个神经元节点. 因而,处理不同时隙下相同指标的神经元具有相同的映射处理函数,而不同的指标级别映射函数不同. 通过此层的级别映射函数,用以实现指标数值和指标状态的模糊化映射.
3) 规则层
规则层用于时序规则、指标规则及其他规则的分析发现.
时序规则分析:每个时序规则分析神经元和预处理层中处理不同时隙相同指标的τ个神经元连接,其中对应n个时序规则分析神经元.
指标规则分析:本层的τ(故障预测中数据窗大小)个神经元同预处理层的处理相同时隙内各指标的n个神经元连接.
其他规则分析:不同时隙下不同指标同故障的关联关系有多种可能性,要全覆盖这种关联关系需要数目庞大的神经元. 此处取ε个神经元同上层神经元建立全连接关系,然后通过算法训练连接权重以实现对这种关联关系的表达.
本层每个神经元节点输出一条规则,这些规则的表达通过指标权重W={ωxy}(x=1,2,…,τn,y=1,2,…,τ+n+ε)体现.
4) 模式层
模式层对应2类模式:故障倾向模式和无故障模式. 它们分别用2个神经元表示. 本层神经元节点同规则层神经元节点建立全连接,进而可基于输入的各种规则及组合权重计算输入指标处于对应模式的概率P.
模式层输出的映射关系是反向传播(BP,back propagation)网络的学习结果,其与规则层的输出及对应的权重组合V={vij}(i=1,2,…,n+τ+ε,j=1,2)相关,用于发现和表达各类规则组合同故障的关系,形成各类表征系统状态的模式.
5) 输出层
输出层包含一个神经元节点,将模式层中概率最大的模式作为预测结果输出.
2 规则发现 2.1 模型参数初始化1) 规则表达ωij的初始化
在规则发现中,定义时间影响因子ft用以表达不同时隙获得的指标对未来故障预测的不同影响. 具体而言,定义σij为指标权重中指标采集时间对故障预测的影响,具体表示为
| $ {\sigma _{ij}} = \exp \left[ {\left( { - \frac{{\tau - i}}{\tau }} \right) \times \ln \left( {{f_t}} \right)} \right] $ | (1) |
此外,定义框架间隔为同类型指标超过阈值连续产生告警的时间间隔T=(Δτ1,Δτ2,…,Δτn);定义告警间隔指标为一个框架间隔内告警发生的次数N=(n1,n2,…,nn);定义R=(γ1,γ2,…,γn)为同类型连续告警间隔内发生故障的比例,用以描述指标中同类型指标告警和故障间的关联. δij表示指标权重中指标特性对故障预测的影响:
| $ {\delta _{ij}}∝\frac{{{n_i}{\gamma _i}}}{{\Delta {\tau _i}}} $ | (2) |
因而,最后的规则层权重为式(1)和式(2)中权重及可调权重φij之和:
| $ {\omega _{ij}} = {\sigma _{ij}} + {\delta _{ij}} + {\varphi _{ij}} $ | (3) |
其中:φij为模型训练中的可调部分,在模型训练中通过σij和δij的初始化,可帮助确定算法收敛方向.
2) 规则层神经元的阈值初始化
时序规则、指标规则及其他规则分析神经元的阈值分别初始化为$\frac{1}{\tau }$、$\frac{1}{n}$和$\frac{1}{\varepsilon }$.
3) 规则关联表达vij及阈值的初始化
规则关联表达用于发现指标规则和故障的关联模式,初始化为[0,1]间的任意随机数;模式层神经元阈值${v_i} = \frac{1}{2}\left( {i = 1,2} \right)$.
2.2 后向传播1) 误差
模型输出误差E为
| $ E = \frac{1}{2}\sum\limits_{i = 1}^2 {{{\left( {{P_i} - {d_i}} \right)}^2}} $ | (4) |
其中:di为模式层第i个节点的期望输出,Pi为对应节点的实际输出.
2) 权重修改
按误差函数E的负梯度方向修改权重系数,取修正后的权值,如式(5)和式(6)所示. 其中,dx为预处理层神经元x的输出;Ly为规则层神经元y的输出;ωxy为预处理层第x个节点与规则层第y个节点的连接权重;vij为规则层第i个节点与模式层第j个节点的连接权重;η为学习因子,α为平滑因子,且满足0 < η,α < 1. 权值修正方案可保证算法收敛快,权值平滑变化.
| $ {\begin{array}{*{20}{c}} {{\omega _{xy}}\left( {t + 1} \right) = {\omega _{xy}}\left( t \right) + \eta {\zeta _y}{d_x} + }\\ {\alpha \left( {{\omega _{xy}}\left( t \right) - {\omega _{xy}}\left( {t - 1} \right)} \right)}\\ {{\zeta _y} = {L_y}\left( {1 - {L_y}} \right)\sum\limits_{k = 1}^2 {{\delta _k}{\upsilon _{yk}}} }\\ {x = 1,2, \cdots ,\tau + n + \varepsilon } \end{array}} $ | (5) |
| $ {\begin{array}{*{20}{c}} {{\upsilon _{ij}}\left( {t + 1} \right) = {\upsilon _{ij}}\left( t \right) + \eta {\zeta _j}{L_i} + \alpha \left( {{\upsilon _{ij}}\left( t \right) - {\upsilon _{ij}}\left( {t - 1} \right)} \right)}\\ {{\zeta _j} = {P_j}\left( {1 - {P_j}} \right)\left( {{d_j} - {P_j}} \right)}\\ {i = 1,2, \cdots ,\tau + n + \varepsilon ;j = 1,2} \end{array}} $ | (6) |
通过Matlab仿真对故障进行预测. 仿真实验的数据来源于某网管系统采集的被管系统性能数据,实验中提取了包含CPU利用率、内存占用率、链路丢包率等性能指标,用于故障关联规则的发现以及故障的预测. 预测中,不针对故障的具体类型进行分类. 采集的性能数据中,每个时隙内上报的告警数变化很大,表明了实验数据中告警和故障间存在数量和时序上的因果关系,且实验中故障的分布随机而不均匀. 此外,ARD_FNN是针对多指标数据进行的,在算法执行中,还需要设置预测数据窗口、预测预留时间、预测窗口等参数.
3.2 算法性能图 2所示为多次进行模型训练后对收敛速度取均值的对比结果. 由图 2可知,ARD_FNN的平均误差为0.12,小于对比算法FNN的误差0.42;训练800次后,误差趋于阈值0.002,而对比算法经过1 000次训练后趋于阈值. 因此,所提出的带有参数初始化的方法较之传统FNN算法在收敛速度和训练时间上得到明显改善.
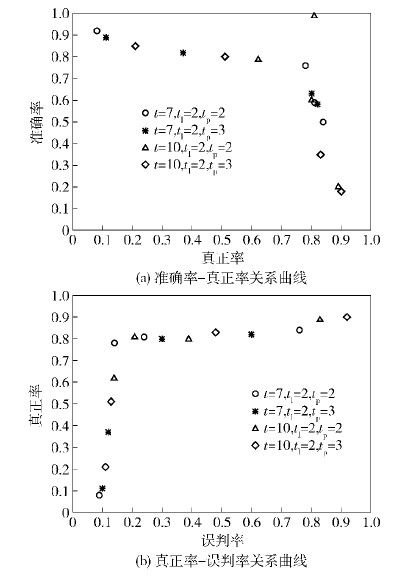
图 3所示为通过调节参数(τ,Δtl,Δtp)获取的准确率-真正率和真正率-误判率关系曲线. 不同的点代表不同参数取值下获得的性能数据. 图 3(a)为准确率-真正率关系曲线,由于准确率和真正率成反比关系,提高准确率的同时会导致真正率降低,反之亦然;通过图中每个节点可计算F-measure,最大可达0.770 0. 图 3(b)为评估模型区分故障态和非故障态能力的真正率-误判率关系曲线,真正率和误判率同样成反比关系,真正率的提高会导致误判率的下降,反之亦然.
图 4所示为算法累计运行开销. 图中选取16个故障点数据(图中黑色实心三角符标注),为了实现对比,加入两条曲线“完全准确预测”和“无预测”,分别表示可准确预测所有故障的情况以及没有故障预测能力的情况. 同时,引入文献[5]中介绍的算法隐半马尔可夫模型(HSMM,hidden semi-Markov model)作为对比. 预测运行的20个时隙内发生的16个故障,对比算法准确预测了14个故障的发生,误报2个故障,还有2个故障没能及时预警,致使累计运行时间增加;而ARD_FNN方法准确预测15个故障,误报1个故障,漏报了1个故障. 因而随着预测持续进行,ARD_FNN在故障预测性能上呈现优势.
提出的ARD_FNN方法在F-measure达到最大值(0.770 0)时,算法准确度s=0.889 3,真正率q=0.679 0. 由前面分析可知,ARD_FNN中训练时间较之其他预测技术明显减少,即所提算法中牺牲部分算法性能换取时间效率,实现在可接受预测效率的前提下算法运行时间明显降低. 表 1所示为文献[5]中HSMM和文献[2]中行为模型频率项分析(FABM,frequency analysis of behavior model) 同ARD_FNN算法在性能上的对比.
| 表1 预测算法在性能上的对比 |
利用FNN的学习能力和模糊推理能力,提出了一种基于FNN的规则发现方法. 该方法用于网管系统中多指标和故障触发间的规则分析和发现,进而实现故障预测. 在方法的模型训练阶段,采用BP算法对模型中预处理层至模式层间的参数进行训练,并且按照多指标和故障触发的时序关系及指标映射关系对模型参数进行初始化. 仿真实验结果表明,通过有效的参数初始化确定了算法收敛方向,加速了算法收敛速度;方法能准确预测故障的发生,在预测准确度、真正率、误判率等指标性能方面得到优化.
| [1] | Ranganai, Chaparadza. UniFAFF: A unified framework for implementing autonomic fault-management and failure-detection for self-managing networks [J]. International Journal of Network Management, 2009, 19(4): 271-290.[引用本文:1] |
| [2] | Abed H J, Al-Fuqaha A, Khan B. Efficient failure prediction in autonomic networks based on trend and frequency analysis of anomalous patterns [J]. International Journal of Network Management, 2013, 23(3): 186-213.[引用本文:2] |
| [3] | 葛艳, 王薇, 闫传军, 等. 基于模糊神经网络的CDMA网络故障诊断方法[J]. 北京邮电大学学报, 2007, 1: 123-126. Ge Yan, Wang Wei, Yan Chuanjun, et al. A fuzzy neural network based fault diagnosis method for the CDMA network [J]. Journal of Beijing University of Posts and Telecommunications, 2007, 1: 123-126.[引用本文:1] |
| [4] | Salfner F, Schieschke M, Malek M. Predicting failures of computer systems: a case study for a telecommunication system[C]//In Proceedings of the 20th International Conference on Parallel and Distributed Processing. Washington DC, USA: IEEE Computer Society, 2006: 348-355.[引用本文:2] |
| [5] | Salfner F, Malek M. Using hidden semi-Markov models for effective online failure prediction [C] //In Proceedings of the 26th IEEE International Symposium on Reliable Distributed Systems. Beijing, China: IEEE, 2007: 161-174.[引用本文:2] |