使用压电方程结合梁弯曲公式和有限元仿真的方法建立了三叠片式压电加速度传感器的数学模型,通过实验验证了模型的正确性. 对三叠片式压电加速度传感器的结构进行了优化设计,在不改变传感器几何轮廓的基础上提高了传感器的灵敏度,并定量分析了不同的结构对传感器性能的影响. 提出了三叠片式压电加速度传感器在矢量水听器中的应用方案,使用有限元法对矢量水听器进行了分析计算,制作了矢量水听器样品并对其主要性能进行了测试.
The sensitivity equation of the bimorph type piezoelectric acceleration sensor was derived from the piezoelectric constitutive equation and the bending formula of cantilever, the finite element method was also used to build the model of the sensor. A method of improving the performance of the acceleration sensor by fabricating hollow structure on surfaces of the metal beam part was analyzed by using finite element method. A vector hydrophone by using bimorph type acceleration sensors was designed, modeled and tested.
同振式矢量水听器中内置了测振传感器，可以直接拾取水下声场中的质点振速信号，单个传感器即可实现对水中声源的定位，作为水下声学接收系统的重要组成部分，广泛应用于海洋环境噪声监测、声纳浮标、潜艇探测和水声通信等领域[1, 2]. 矢量水听器的研制和性能改进受到了国内外普遍重视. 水下声场中质点振速幅值通常很小，三叠片式压电加速度传感器具有结构简单、高灵敏、易于小型化但耐冲击性差等优缺点，适合应用在矢量水听器中，国内外对此进行了大量研究[3, 4].
笔者以三叠片式加速度传感器为对象，建立了数学模型，模型可有效反映几何参数、材料参数和末端固定方式等因素对其性能的影响，通过结构改进等方式优化了其性能，并设计、制作和测试了内置三叠片式压电加速度传感器的矢量水听器.
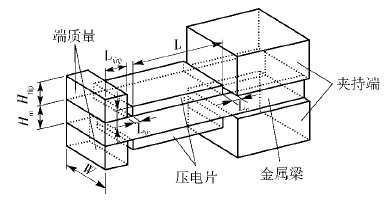
1 加速度传感器的建模和实验 1.1 压电方程结合梁弯曲公式建立的模型三叠片式压电加速度计的基本结构如图 1所示，图中两片压电片极化方向相反，相互之间为电学串联.
|
图1 三叠片式压电加速度传感器的结构示意图 |
令垂直于传感器长度和宽度方向的外加电场为0，此时压电方程可简化为
| $ {D_3} = {d_{31}}T_1^p $ | (1) |
其中：D3为电位移，d31为横向压电系数，T1p为压电片长度方向上的弯曲正应力. 在对传感器进行受力分析时，除了沿梁长方向的弯曲正应力外，假定其他方向的应力为0. 忽略自由端质量块和压电片之间、压电片和夹持端之间的缝隙Ltc和Lc，并将质量块的几何结构简化为梁自由端处的一个质点，质量块之间的金属梁部分视为质量块的一部分. 在加速度载荷a的作用下，质量块对梁部分的作用可以简化为梁距夹持端L处的集中力Ftip(见式(2))，传感器其余部分的惯性力表示为均布载荷ω(见式(3)).
| $ {F_{{\rm{tip}}}} = {L_{{\rm{tip}}}}{\rm{W}}\left( {2{\rho _{{\rm{tip}}}}{H_{{\rm{tip}}}} + {\rho _{\rm{m}}}{H_{\rm{m}}}} \right)a $ | (2) |
| $ \omega = \left( {2{\rho _{\rm{c}}}{H_{\rm{c}}} + {\rho _{\rm{m}}}{H_{\rm{m}}}} \right)Wa $ | (3) |
其中：Ltip为端质量的长度，W为传感器的宽度，Htip为端质量的高度，Hm为金属梁的厚度，Hc为压电片的厚度，ρtip为端质量的密度，ρm为金属梁的密度，ρc为压电片的密度.
简化后的三叠片式压电加速度传感器由压电材料和金属材料组成. 通过将压电材料类比为金属材料，可以将求复合梁弯曲正应力的问题转化为求单一材料悬臂梁弯曲正应力的问题. 类比后压电片的宽度变为nW，其中n为转换系数：
| $ n = {E_{\rm{c}}}/{E_{\rm{m}}} $ | (4) |
其中：Ec为压电片的弹性模量，Em为金属梁的弹性模量.
传感器的截面惯性矩I为
| $ I = \frac{1}{{12}}WH_{\rm{m}}^3 + 2\left[ {\frac{1}{{12}}nWH_{\rm{c}}^3 + nW{H_{\rm{c}}}{{\left( {\frac{{{H_{\rm{c}}} + {H_{\rm{m}}}}}{2}} \right)}^2}} \right] $ | (5) |
由悬臂梁的弯曲正应力公式，可求得距夹持端x处压电片中性层处的弯曲正应力σ(x)为
| $ \sigma \left( x \right) = - \frac{{nM\left( x \right)\left( {\frac{{{H_{\rm{c}}} + {H_{\rm{m}}}}}{2}} \right)}}{I} $ | (6) |
将式(6)代入式(1)，得到传感器在加速度静载荷a作用下产生的总电荷量Q为
| $ Q = {d_{31}}W\int_0^L {\sigma \left( x \right){\rm{d}}x} $ | (7) |
将式(5)和式(6)代入式(7)，可以得到三叠片式压电加速度传感器的电荷灵敏度SQ为
| $ \begin{array}{*{20}{c}} {{S_Q} = \frac{Q}{a} = {d_{31}}{E_{\rm{c}}}{L^2}W\left( {{H_{\rm{c}}} + {H_{\rm{m}}}} \right)\left( {2{\rho _{\rm{c}}}L{H_{\rm{c}}} + } \right.}\\ {\left. {{\rho _{\rm{m}}}L{H_{\rm{m}}} + 6{\rho _{{\rm{tip}}}}{L_{{\rm{tip}}}}{H_{{\rm{tip}}}} + 3{\rho _{\rm{m}}}{L_{{\rm{tip}}}}{H_{\rm{m}}}} \right)/}\\ {\left( {8{E_{\rm{c}}}H_{\rm{c}}^3 + 12{E_{\rm{c}}}H_{\rm{c}}^2{H_{\rm{m}}} + 6{E_{\rm{c}}}{H_{\rm{c}}}H_{\rm{m}}^2 + {E_{\rm{m}}}H_{\rm{m}}^3} \right)} \end{array} $ | (8) |
通过建立三叠片式压电加速度传感器的有限元模型，可以有效地反映压电片和夹持端之间的缝隙Lc等因素对传感器性能的影响.
根据三叠片式压电加速度传感器的几何参数和材料参数，在有限元分析软件ANSYS中建立传感器的几何模型，并输入包括压电矩阵、刚度矩阵和介电常数等在内的材料参数. 划分网格时，传感器的压电材料部分选用单元SOLID226，金属材料部分选用单元SOLID186，通过定义局部坐标系设定各压电片的极化方向，令压电片上下表面极化方向相反，并平行于其厚度方向，然后添加相应电极面. 传感器的夹持端对传感器的作用简化为对相应节点施加位移约束，并对整个模型施加加速度载荷. 通过静态分析、模态分析和谐响应分析，可以计算得到传感器的灵敏度、静态电容、谐振频率和灵敏度幅频特性.
1.3 模型的实验验证制作了电学串联状态的三叠片式压电加速度传感器样品，并用螺钉和夹持片将其固定在基座上，如图 2所示. 样品中压电材料为压电陶瓷PZT-5H，金属梁和端质量材料为不锈钢，基座和夹持片的材料为铝合金. 几何、材料参数如表 1和表 2所示，其中ε33T为相对介电常数.
|
图2 三叠片式压电加速度传感器样品 |
 | 表1 样品几何参数 |
| 表2 样品材料参数 |
分别使用1.1节和1.2节中建立的模型计算三叠片式压电加速度传感器的电荷灵敏度，结果分别为0.38和0.42 pC·m-1·s2. 通过有限元计算和实验得到加速度传感器样品在2 kHz频率范围内的电荷灵敏度幅频特性如图 3所示. 有限元计算得到的结果和实验结果有很好的一致性，验证了所建立模型的有效性，其中压电方程结合梁弯曲公式建立的模型得到的结果略低于实验结果. 通过使用这两种传感器的数学模型，可以分析几何和材料参数等对传感器性能的影响，从而有效地指导三叠片式压电加速度传感器的设计. 在定量分析时，应使用有限元模型以保证结果的准确性.
|
图3 传感器的灵敏度幅频特性 |
通过在传感器的金属梁部分加工镂空结构，可以在提高传感器灵敏度的同时不改变传感器的轮廓外形，并减轻传感器的质量.
典型的镂空结构有弧形孔阵列，如图 4所示. 在传感器的金属梁部分加工镂空孔，一方面降低了传感器的整体抗弯刚度；另一方面降低了传感器的质量. 传感器弯曲刚度的降低会导致其灵敏度上升，谐振频率下降，而质量降低带来的影响则恰好相反. 镂空结构造成的这两种截然相反的影响使这种优化方法更适用于那些压电材料较“软”、端质量较“重”、金属梁材料比较“轻”和“硬”的传感器. 因为满足上述条件的传感器，镂空结构降低传感器弯曲刚度的效果得到凸显，降低传感器质量的效果弱化. 尺寸和数量不同的镂空孔对传感器性能的影响不同，通过对镂空结构进行设计，可以灵活有效地调节传感器包括灵敏度和谐振频率在内的各项参数.
|
图4 无镂空孔和有弧形镂空孔压电片结构 |
通过建立具有镂空结构的传感器有限元模型，可以分析不同镂空结构对传感器性能的影响. 以1.3节中三叠片式加速度传感器为优化对象，分析弧形镂空的变化对传感器性能的影响.
令弧形孔的个数为3，单个弧形孔的跨度为1 mm，弧形孔边缘距离压电片两端边缘均为0.5 mm. 当镂空孔深为0.5 mm时，使用有限元法计算得到传感器的性能变化如表 3所示，其中括号中的数字表示有镂空孔和无镂空孔的传感器对应性能参数之比.
| 表3 镂空孔几何参数 |
由式(7)可知，在加速度载荷作用下，三叠片式压电加速度传感器产生的电荷量和压电片上沿长度方向上弯曲正应力的积分成正比. 以图 4所示传感器压电片上1号点为起点，2号点为终点，使用有限元软件计算得到无镂空孔传感器和有弧形镂空孔传感器的压电片表面起点和终点之间沿长度方向上的弯曲正应力分布如图 5所示. 从图 5中可以直观地看到，压电片上沿梁长方向上弯曲正应力的积分(图 5中对应曲线下方的面积). 在金属梁上加工镂空孔的悬臂梁式压电加速度传感器的弯曲正应力积分明显大于无镂空结构的传感器，造成有镂空孔的加速度传感器的电荷灵敏度高于无镂空孔的结果.
|
图5 加速度计压电片上沿长度方向的弯曲正应力分布 |
基于有限元分析方法，设计了一个上限频率约为500 Hz的胶囊形同振式矢量水听器. 矢量水听器的矢量通道由3个正交安装的自制三叠片式压电加速度传感器(金属梁部分没有加工镂空结构)组成. 加速度传感器安装在由低密度材料加工的主体的中心位置，标量通道为压电陶瓷圆管结构的声压传感器，压电圆管和主体之间存在空气腔，样品整体使用聚氨酯灌封.
使用安装了压电和声学扩展模块的ANSYS Workbench仿真软件并结合APDL命令流对内置压电加速度计的矢量水听器的性能进行分析，可以直接计算得到在给定的水下平面声波的激励下矢量水听器标、矢量通道输出电信号的频响特性. 分析过程中忽略了线缆、螺钉等对矢量水听器样品性能影响较小的部分.
3.2 矢量水听器样品的制作和测试矢量水听器样品如图 6所示. 灌封后的矢量水听器样品半径为32 mm，圆柱部分高度为45 mm，平均密度为1.2 g/cm3.
|
图6 矢量水听器样品 |
矢量水听器样品在驻波管中采用比较法进行了测试. 标、矢量通道的自由场声压灵敏度幅频特性测试结果、200 Hz的指向性测试结果如图 7所示. 矢量水听器样品的测试结果和有限元计算结果吻合得较好，3个矢量通道的声压灵敏度级具有较好的一致性，满足每倍频程6 dB的变化规律，并具有较好“8”字形指向性.
|
图7 标、矢量通道的指向性测试结果 |
使用压电方程结合梁弯曲公式和有限元法建立了三叠片式压电加速度传感器的数学模型，并通过实验验证了模型的正确性. 模型对传感器的设计提供了有效的指导. 给出了在金属梁上加工镂空结构的传感器性能优化方案，可以在不改变加速度计轮廓结构、减轻加速度计质量的基础上增大其灵敏度. 设计了内置三叠片式压电加速度传感器的矢量水听器，用有限元法分析了在水下平面声波的激励下，矢量水听器标、矢量通道输出电信号的频响特性. 制作了矢量水听器的样品并测试了其主要性能，测试结果和有限元计算结果具有很好的一致性.
| [1] | 贾志富. 全面感知水声信息的新传感器技术——矢量水听器及其应用[J]. 物理, 2009, 38(3): 157-168. Jia Zhifu. Novel sensor technology for comprehensive underwater acoustic information-vector hydrophones and their applications[J]. Physics, 2009, 38(3): 157-168.[引用本文:1] |
| [2] | Abdi A, GuoHuaihai, Sutthiwan P. A new vector sensor receiver for underwater acoustic communication[C]//OCEANS 2007. Vancouver: IEEE Press, 2007: 1-10.[引用本文:1] |
| [3] | Mark B Moett, D H Trivett, Patrick J Klippel, et al. A piezoelectric, flexural-disk, neutrally buoyant, underwater accelerometer[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 1998, 45(5): 1341-1346.[引用本文:1] |
| [4] | 尹义龙, 李俊宝, 邢建新, 等. 弛豫铁电单晶弯曲梁矢量水听器研究[J]. 声学学报, 2014, 39(2): 243-250. Yin Yilong, Li Junbao, Xing Jianxin, et al. Research on the relaxor ferroelectric single crystal flexural beam vector hydrophone[J]. Acta Acustica, 2014, 39(2): 243-250.[引用本文:1] |