2. 航天恒星科技有限公司, 北京 100086
针对跳频信号的欠定盲源分离,为了解决现有的时频域方法中算法计算量大、信号存在畸变、恢复精度不高的问题,提出了一种基于滤波的跳频信号欠定盲分离算法. 该算法首先根据估计到的源信号载频设计带通滤波器,利用这些滤波器对观察信号进行滤波,得到只包含某一个源信号的观测信号分量,使原分离问题分为数个时域上稀疏的欠定盲分离问题,然后对各个分量在时域上分别应用欠定盲源分离算法估计每跳数据. 通过仿真对比发现,所提的滤波法得到的跳频信号更精确,信干比比时频域方法大4dB;同时所提算法处理的数据量小,计算复杂度低.
2. Space Star Technology Company Limited, Beijing 100086, China
Aiming at the underdetermined blind source separation (UBSS) of frequency hopping, a UBSS algorithm based on filtering was proposed to solve the problems of high computation and low estimated accuracy of signal caused by distortion method in existing time-frequency domain. Firstly, according to the estimated carrier frequencies, some kinds of band pass filters were designed. And the observed signals were filtered by using these band pass filters. After that, we can get the filter signals just composed of one source signal. Thus, the original UBSS problem was transferred into several UBSS problems in which the sparsity in time domain is satisfied. Finally, according to the filtered signals, the source signal was estimated by using the time domain UBSS algorithm. Simulation show that proposed algorithm can get more accurate estimated signals and have fewer processing data and lower computation complexity. The signal to interference ratio o of proposed algorithm is 4dB bigger than that of time-frequency domain method.
目前,大多数欠定盲源分离(UBSS,under-determined blind source separation)算法都基于稀疏分量分析理论,按照两步法进行. 张烨等[1]首次在传统的两步法基础上提出将最新的压缩感知技术应用于源信号的分离中,与传统的两步法相比取得了较好的分离结果.
近年来,由于跳频信号的广泛应用,多个混合跳频信号的分离问题也成为一项研究热点. 马捷等[2]和顾晨辉等[3]提出利用跳频信号的某些特征参数完成跳频信号分选,但是不能恢复出跳频信号数据,给后续的解调、解密处理带来了一定困难. Wang等[4]和Feng等[5]提出利用盲源分离技术解决跳频信号的恢复问题,但该算法要求接收天线数目大于等于源信号数目,对于欠定混合条件下的跳频信号恢复,算法失效. Sha等[6]提出一种基于时频域转换方式的跳频信号UBSS算法,时频域算法需要对信号进行重叠加窗的短时傅里叶变换和反变换,因此处理的数据量大,计算复杂度高;同时,加窗带来的信号畸变导致恢复出来的信号准确度低.
针对以上问题,笔者提出一种基于滤波的跳频信号UBSS算法. 首先对跳频信号进行滤波处理,将其时域数据稀疏化,然后应用UBSS算法即可直接恢复出源信号的时域数据. 相对时频域方法,该算法由于省略了重叠加窗的短时傅里叶变换和反变换,因此减小了处理的数据量以及由于加窗带来的信号畸变,在提高恢复精度的同时,大大降低了计算复杂度.
1 跳频信号分离模型若在接收时间段Δt内同步正交跳频电台发射了N个跳频源信号,分别是s1(t),s2(t),…,sN(t). sn(t)为
| $ {{s}_{n}}\left( t \right)={{a}_{n}}\left( t \right){{e}^{j[{{\omega }_{n}}\left( t \right)t+{{\varphi }_{n}}\left( t \right)]}} $ | (1) |
其中:an(t)为第n个跳频信号sn(t)的基带复包络,ωn(t)、φn(t)分别为跳频在t时刻的载频及相位. 假设接收天线是M个阵元的均匀线型阵(ULA,uniform linear array),阵元间距为d(d<λmin /2,λmin =c/fmax ( c为光速,fmax 为信号最高载频). 传输距离和发射角度的不同导致信号到达不同阵元的时间不同,即存在时延. 设第n个信源在ULA上的入射角为θn,则每个阵元所接收到的信号时延为
| $ {{\tau }_{m,n}}=\frac{1}{c}\left( m-1 \right)d\sin {{\theta }_{n}}=\left( m-1 \right)\Delta {{\tau }_{n}} $ | (2) |
第n个源信号在第m个阵元上的感应信号为
| $ \begin{array}{l} {x_{m,n}}\left( t \right) = {A_{mn}}{s_n}\left( {t - {\tau _{mn}}} \right) + {v_m}\left( t \right) = \\ {A_{mn}}{a_n}\left( {t - {\tau _{mn}}} \right){e^{j[{\omega _n}\left( {t - {\tau _{mn}}} \right)\left( {t - {\tau _{mn}}} \right) + {\varphi _n}\left( {t - {\tau _{mn}}} \right)]}} + {v_m}\left( t \right) \end{array} $ | (3) |
其中:Amn为第m根天线对第n个源信号幅度上的失配系数,对于慢衰落信道,可假设Amn=1是常数;vm(t)为第m个接收天线接收到的噪声. 若调制分量是缓缓的逐渐改变的信号(带宽很窄),在时延τ内没有发生载频跳变,信号幅度没有减小,那么有
| $ \left. \begin{array}{l} a\left( {t - \tau } \right) \approx a\left( t \right)\\ \varphi \left( {t - \tau } \right) \approx \varphi \left( t \right)\\ \omega \left( {t - \tau } \right) \approx \omega \left( t \right) \end{array} \right\} $ | (4) |
则式(3)可重写成
| $ {x_{mn}}\left( t \right) = {s_n}\left( t \right){e^{ - j{\omega _n}\left( t \right){\tau _{mn}}}} + v\left( t \right) $ | (5) |
N个跳频源信号在第m个阵元上总的感应信号为
| $ \begin{array}{l} {x_m}\left( t \right) = \sum\limits_{n = 1}^N {{x_{mn}}\left( t \right) + v\left( t \right) = } \\ \sum\limits_{n = 1}^N {{s_n}\left( t \right){e^{ - j{\omega _n}\left( t \right){\tau _{mn}}}}} + v\left( t \right) \end{array} $ | (6) |
用矩阵形式表示M个阵元在任意的t时刻接收到的时域信号为
| $ x\left( t \right) = A\left( t \right)s\left( t \right) + v\left( t \right) $ | (7) |
其中A(t)为在ULA接收情形下的信道矩阵,表示为
| $ A\left( t \right) = \left[{\begin{array}{*{20}{c}} 1&1& \cdots &1\\ {{e^{ - j{\omega _1}\left( t \right){\tau _{21}}}}}&{{e^{ - j{\omega _1}\left( t \right){\tau _{22}}}}}& \cdots &{{e^{ - j{\omega _1}\left( t \right){\tau _{2N}}}}}\\ \vdots & \vdots &{}& \vdots \\ {{e^{ - j{\omega _1}\left( t \right){\tau _{M1}}}}}&{{e^{ - j{\omega _1}\left( t \right){\tau _{M2}}}}}& \cdots &{{e^{ - j{\omega _1}\left( t \right){\tau _{MN}}}}} \end{array}} \right] $ | (8) |
由式(7)可以看出,混合矩阵A随着载频发生变化,是时变的,而每一跳之内混合矩阵不变,所以要对跳频信号应用UBSS算法,必须将跳频信号按跳数划分,保证每跳中混合矩阵不发生变化,然后分别对每跳信号进行UBSS. 这里假设同步正交跳频信号相关参数(跳周期、载频等)已经利用现有算法估计得到[7, 8].
2 基于滤波的跳频信号UBSS由UBSS理论可知,要解决跳频信号的UBSS问题,首先需要解决跳频信号时域不满足稀疏性要求的问题. 虽然将跳频信号转换到时频域可以解决这个问题,但直接得到的只是跳频信号的时频域数据,而对于以得到时域数据为恢复目标的跳频信号盲分离,仍需进行一次傅里叶反变换才能得到最终要求的时域数据. 可以看到,这种需要进行傅里叶变换和反变换的处理方式增加了算法的复杂度.
考虑某一跳内跳频信号UBSS模型:
| $ \left( {\begin{array}{*{20}{c}} {{x_1}\left( t \right)}\\ {{x_2}\left( t \right)} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{a_{11}}}&{{a_{12}}}&{{a_{13}}}&{{a_{14}}}\\ {{a_{21}}}&{{a_{22}}}&{{a_{23}}}&{{a_{24}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{s_1}\left( t \right)}\\ {{s_2}\left( t \right)}\\ {{s_3}\left( t \right)}\\ {{s_4}\left( t \right)} \end{array}} \right) $ | (9) |
以第1个观测信号为例,x1(t)=a11s1(t)+a12s2(t)+a13s3(t)+a14s4(t)分别包含4个源信号的频率分量,由于4个同步正交跳频源信号的载频各不相同,且载频信息可以通过跳频信号参数估计算法得到,那么可以让观测信号通过一个中心频率为fj、带宽为跳频信号最小频率间隔的带通滤波器Hn(n=1,2,3,4),该滤波器通带内的增益为0,分别滤出包含各个频率信息的观测信号分量.
那么原UBSS模型可转换为
| $ \left( {\begin{array}{*{20}{c}} {x_1^n\left( t \right)}\\ {x_2^n\left( t \right)} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{a_{1n}}}\\ {{a_{2n}}} \end{array}} \right){s_n}\left( t \right),n = 1,2,3,4 $ | (10) |
即
| $ {x^n}\left( t \right) = {A_n}{s_n}\left( t \right) $ |
其中: $ {x^n}\left( t \right) = \left( {\begin{array}{*{20}{c}} {x_1^n\left( t \right)}\\ {x_2^n\left( t \right)} \end{array}} \right) $为第m个观察信号通过第n个滤波器后得到的向量,An为混合矩阵A的第n列.
可见,通过滤波可以将原UBSS问题分解为4个UBSS问题,且在每一个分解后的模型中,跳频源信号都是充分稀疏的. 由式(10)可知
| $ \frac{{x_2^n\left( t \right)}}{{x_1^n\left( t \right)}} = \frac{{{a_{2n}}}}{{{a_{1n}}}},n = 1,2,3,4 $ | (11) |
即 $ \frac{{x_2^n\left( t \right)}}{{x_1^n\left( t \right)}} = $理论上是一个常数,但是由于噪声等的影响,$ \frac{{x_2^n\left( t \right)}}{{x_1^n\left( t \right)}} = $在不同时间t上往往并不完全相等,但是都会集中在 $ {{\tilde a}_n} \buildrel \Delta \over = \frac{{{a_{2n}}}}{{{a_{1n}}}} $附近,因此可以对所有时刻的 $ \frac{{x_2^n\left( t \right)}}{{x_1^n\left( t \right)}}$进行聚类(即求均值),得到的聚类中心就是 $ {{\tilde a}_n} $的估计值,用 $ {{\hat a}_n} $表示,则混合矩阵的第n个列向量的估计值 $ {{\hat A}_n} $为
| $ {{\hat A}_n} = \left[{\begin{array}{*{20}{c}} 1\\ {{{\hat a}_n}} \end{array}} \right] $ | (12) |
在得到混合矩阵以后,就可以估计出源信号,由式(10)可知
| $ {{\hat s}_n}\left( t \right) = {\left( {\begin{array}{*{20}{c}} {{a_{1n}}}\\ {{a_{2n}}} \end{array}} \right)^†}\left( {\begin{array}{*{20}{c}} {x_1^n\left( t \right)}\\ {x_2^n\left( t \right)} \end{array}} \right),n = 1,2,3,4 $ | (13) |
其中(·)† 表示对矩阵求伪逆.
3 算法步骤观测信号数目取2,源信号数目取4,以统计稀疏分解原则算法为例,对于某一跳信号,基于滤波的跳频信号UBSS算法具体步骤如下:
1) 根据估计得到的4个源信号的载频生成4个带通滤波器,让观测信号通过滤波器得到包含各个源信号频率分量的4个观测信号分量;
2) 分别求取4个观测信号分量中数据的比值,并计算其平均值,得到聚类中心,由此根据式(12)即可得到该跳混合矩阵列向量的估计值;
3) 根据每一个滤波后的信号向量和估计到的混合矩阵列向量,利用式(13)来估计源信号.
对剩下的每跳观测信号分别应用上述算法,即可得到源信号所有跳的时域数据.
4 算法仿真与结果分析用于仿真的参数:跳频源信号数目为4,采样频率为20MHz,调制方式采用二进制相位调制,4个源信号的符号速率分别为20kbit/s、40kbit/s、25kbit/s及50kbit/s,跳速为1000跳/s,接收天线选用ULA,天线间距取半波长,信号到达角为20°、60°、80°、50°. 每次仿真处理3跳数据,跳频频率矩阵为
| $ {f_c} = \left[{\begin{array}{*{20}{c}} 8&6&2\\ {6.5}&{3.5}&5\\ {7.5}&1&6\\ 3&{6.5}&4 \end{array}} \right] $ |
为了定量地衡量算法的混合矩阵估计精确度,定义混合矩阵估计误差EA为
| $ {E_A} = 10\lg \left( {\frac{1}{N}{{\left\| {A - \hat A} \right\|}_F}} \right) $ | (14) |
其中:‖·‖F表示Fro范数,A为真实混合矩阵,$ {\hat A}$ 为估计值,N为跳频源信号数目. EA越小,估计准确度越高.
为了衡量所得时域跳频信号的精确度,利用式(15)所示的信干比γ进行衡量[5].
| $ \gamma = 10\lg \left( {\frac{{\sum\limits_{n = 1}^N {E\left\{ {s_n^2\left( t \right)} \right\}} }}{{\sum\limits_{n = 1}^N {E\left\{ {{s_n}\left( t \right) - {{\hat s}_n}{{\left( t \right)}^2}} \right\}} }}} \right) $ | (15) |
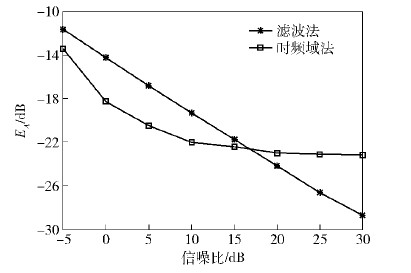
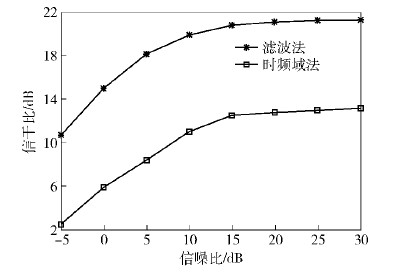
图 1给出了不同信噪比条件下所提算法(简称滤波法)与时频域方法的混合矩阵估计误差. 图 2给出了不同信噪比条件下滤波法和时频域方法所估计的时域跳频信号的信干比对比结果.
从图 1中可以看到,当信噪比较小(小于16dB)时,滤波法估计得到的混合矩阵误差比时频域方法略高;当信噪比较大时,则滤波法估计的混合矩阵误差更小. 这是因为时频域方法进行时频变换后,信号能量集中在信号载频附近,其他地方的信号都当作噪声进行处理,所以有一定的抗噪能力. 信噪比越小,噪声影响越大,因此时频域方法的优势越明显. 但是由于时频域方法对信号进行了加窗的短时傅里叶变换,所以信号会产生一定的畸变. 当信噪比较大时,噪声的影响很小,而时频域方法加窗引起的信号畸变的影响相对更大,因此,此时混合矩阵的估计反而不如滤波法. 从图 1还可以看到,当信噪比大于20dB时,随着信噪比的增大,时频域方法混合矩阵估计误差基本不变,而滤波法则继续下降. 这就是因为时频域方法中信号存在畸变,所以虽然信噪比在增大,但混合矩阵估计误差却不变.
由图 2可以看到,滤波法所估计的时域跳频信号的信干比明显大于时频域方法. 在相同信噪比条件下,滤波法比时频域方法所得信干比提高4dB以上. 这是因为尽管信噪比较小时,滤波法估计的混合矩阵准确性不如时频域方法,但是时频域方法中信号存在畸变,因此滤波法恢复出来的时域跳频信号信干比要大于时频域方法. 而跳频信号UBSS的最终目的是估计出跳频源信号,因此从这方面来说,提出的滤波法要优于时频域方法.
另一方面,由于时频域方法需要对信号进行重叠加窗的短时傅里叶变换和反变换,所以数据存储量和运算复杂度较高;而提出的滤波法只需对信号进行N次滤波即可,数据存储量小,运算复杂度低. 如在仿真中采样点数为60000,源信号数目为4的情况下,短时傅里叶变换长度即窗长取4096,相邻两窗的重叠采样点数为3840,那么时频域转换方式中待处理的数据量为897024,而滤波方式则是将6万个数据处理了4次. 在实际运行时间方面,时频域聚类算法花费0.5559s,所提算法用时0.0321s. 所以在解决跳频信号的UBSS问题时,与现有的时频域转换算法相比,在保证恢复精度的前提下,所提算法的复杂度有明显降低.
5 结束语为了解决现有的时频域方法中算法计算量大、信号存在畸变、恢复精度不高的问题,针对跳频信号的UBSS,提出了一种基于滤波的跳频信号UBSS算法. 该算法首先按照源信号载频设计带通滤波器,得到只包含某一个源信号的观测信号分量,使原分离问题分为数个UBSS问题的线性相加,且每一个滤波得到的观测信号分量组成的模型都满足稀疏分量分析理论的要求,然后再对各个分量分别应用UBSS算法重构每跳数据. 通过仿真对比发现,所提的滤波法得到的跳频信号更精确,信干比比时频域方法大4dB. 同时,由于所提算法省去了加窗的短时傅里叶变换和反变换,可直接处理时域数据,而不是处理数据量远大于时域的时频域数据,因此处理的数据量小,算法复杂度更低.
| [1] | 张烨, 方勇. 基于拉普拉斯势函数的欠定盲分离中源数的估计[J]. 信号处理, 2009, 25(11): 1719-1725. Zhang Ye, Fang Yong. New method to estimate the number of the sources for underdetermined blind separation based on lapulacial potential function[J]. Signal Processing, 2009, 25(11): 1719-1725.[引用本文:1] |
| [2] | 马捷, 俞有光, 钟子发. 一种适用于复杂电磁环境下的跳频信号快速检测方法[J]. 通信对抗, 2010(1): 28-32. Ma Jie, Yu Youguang, Zhong Zifa. An efficient detecting method of frequency hopping signal in complex electromagnetic environment[J]. Communication Countermeasures, 2010(1): 28-32.[引用本文:1] |
| [3] | 顾晨辉, 王伦文. 一种正交跳频信号动态分选算法[J]. 宇航学报, 2012, 33(11): 1699-1705. Gu Chenhui, Wang Lunwen. A method for orthogonal FH signals dynamic sorting[J]. Journal of Astronautics, 2012, 33(11): 1699-1705.[引用本文:1] |
| [4] | Wang Rongjie, Zhan Yiju, Zhou Haifeng. Bind separation method using second-order statistics for multi-hopping frequency signals[J]. Journal of Data Acquisition and Processing, 2011, 26(6): 714-718.[引用本文:1] |
| [5] | Feng Tao, Yuan Chaowei. Blind separation of frequency-hopping signals based on time- frequency distribution[J]. Systems Engineering and Electronics, 2010, 32(5): 900-903.[引用本文:2] |
| [6] | Sha Zhichao, Huang zhitao, Zhou Yiyu, et al. Frequency-hopping signals sorting based on underdetermined blind source separation[J]. IET Communication, 2013, 7 (14) : 1456-1464.[引用本文:1] |
| [7] | 付卫红, 武少豪, 张凡路, 等. 一种基于ARMA模型的欠定混合快速跳频信号参数盲估计算法[J]. 北京邮电大学学报, 2014, 37(5): 17-20. Fu Weihong, Wu Shaohao, Zhang Fanlu, et al. A blind parameter estimation algorithm of fast frequency hopping signals for underdetermined situation based on ARMA model[J]. Journal of Beijing University of Posts and Telecommunications, 2014, 37(5): 17-20.[引用本文:1] |
| [8] | Chen T C. Joint signal parameter estimation of frequency-hopping communications[J]. IET Communication, 2012, 6(4): 381-389.[引用本文:1] |