针对多径信道下分布式多输入多输出正交频分复用系统多载波频偏估计问题和多频偏盲估计难、现有盲估计方法较少的情况,利用多径信道下分布式多输入多输出正交频分复用信号模型与盲源分离领域中信号模型类似的特点,利用卷积混合盲源分离思想,去除接收信号的多径影响及模糊度,得到只含频偏的发送信号,将多维频偏估计问题变成单维估计问题,最后用单个信号频偏盲估计算法得到频偏估计值. 仿真结果表明,提出算法适用于更为复杂的多径信道和正交频分复用信号,具有比导频辅助方法更优的估计性能. 在5dB信噪比下,多频偏盲估计的均方误差可达10-6.
An algorithm of multiple frequency offsets estimation for distributed multiple input multiple output orthogonal frequency division multiplexing (MIMO-OFDM) systems was discussed. Accounting for the difficulty and lack of blind estimation methods, the scheme uses the deconvolution blind source separation (BSS) to distract the effect of multipath and ambiguity and obtain the frequency offset signals by considering that the characteristics of the multipath signal model is similar to the signal in BSS. The multidimensional frequency estimation problem is thus turned into multiple single dimension problems, and then the frequency offset value is obtained by a single frequency offset estimation algorithm. Simulations indicate that the proposed algorithm has better performance in estimating the frequency offsets than pilots-aided ones. Under signal noise ratio (SNR) of 5 dB, the mean square errors of the carrier frequency offset (CFO) reaches to 10-6.
发射天线在地理位置上呈分布式摆放,且分布在不同位置的发射天线由光纤或电缆连接到同一个信号处理中心,这样的多输入多输出(MIMO,multiple input multiple output)系统称为分布式MIMO系统[1]. 分布式系统可以克服远近效应和阴影效应造成的路径损耗,解决小区通信死角的问题,提供更好的小区覆盖率. 正交频分复用(OFDM,multiple input multiple output orthogonal frequency division multiplexing)技术与分布式系统的结合可以有效提高信道容量,使频谱利用率成倍提升. 分布式系统的发送端和接收端之间具有多个频偏、时延和信道系数,接收端收到的是来自不同天线的信号和,需要估计出多个不同的频偏. Yao等[2]发送多个正交的导频,在接收端将导频与接收信号进行相关处理,分离特定发送天线上的信号并估计频偏. Thehanh等[3, 4]采用收敛速度较快的期望最大化算法. Nasir等[5]提出了一种盲估计方法,利用线性盲源分离(BSS,blind source seperation)方法分离接收信号. 笔者考虑多径信道下的分布式多输入多输出正交频分复用(MIMO-OFDM,multiple input multiple output orthogonal frequency division multiplexing)频偏盲估计问题. 利用卷积混合盲源分离思想[6]来实现多径信道下的信号盲分离,将多维估计问题变成单维估计问题,接着利用经典的频偏估计方法即可实现多个1维的频偏估计.
1 分布式MIMO-OFDM信号模型定义Nt为发射端相距很远的天线数,Nr为接收端天线数,分布式通信系统框图如 图 1所示.
其中Xqn为q时刻第n根发射天线发送的频域符号,
| $ \begin{array}{l} X_q^n = {\left\{ {X\left. {_q^n\left( 0 \right),X_q^n\left( 1 \right),\cdots ,X_q^n\left( {N - 1} \right)} \right\}} \right.^T},\\ \;\;\;\;\;\;n = 1,2,\cdots ,{N_t},q = 0,1,\cdots \end{array} $ | (1) |
每个OFDM符号块的子载波数为N,经过反傅里叶变换(IFFT,inverse fast Fourier transform),得到时域信号uqn,随后在OFDM符号块尾部加入K(K≤N)个0,并送入信道进行传输. 第m(1≤m≤Nr)根接收天线上第q个离散时域OFDM符号块可表示为
| $ \begin{array}{l} \sum\limits_{n = 1}^{{N_t}} {{e^{{\rm{j}}\frac{{{\rm{2}}\pi {f_{m,n}}\left( {i + qM} \right)}}{N}}}} \sum\limits_{l = 0}^L {{h_{m,n}}\left( l \right)u_q^n\left( {i - l - {\tau _{m,n}}} \right) + w_q^m\left( i \right),} \\ \;\;\;\;m = 1,2,\cdots ,{N_r},i = 0,1,\cdots M - 1 \end{array} $ | (2) |
其中:hm,n为多径信道响应,路径数为L;τm,n为第n根发射天线到第m根接收天线上的时延;fm,n为第n根发射天线对第m根接收天线的归一化载波频偏(对子载波间隔进行归一化),这里的频偏和信道在多个OFDM符号块内是不变的,并认为所有接收天线共享一个振荡器,因此fm,n可简化为fn;M=N+K为添加了迫零后缀(ZP,zero padding)的OFDM有效长度;wqm(i)为第m根接收天线上的复高斯白噪声,均值为0,方差为σw2. 为了更符合卷积混合信号模型,将式(2)进一步简化为
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;y_q^m\left( i \right) = \\ \sum\limits_{n = 1}^{{N_t}} {{e^{{\rm{j}}\frac{{{\rm{2}}\pi {f_n}\left( {i + qM} \right)}}{N}}}} \sum\limits_{l = {\tau _{m.n}}}^{L + {\tau _{m.n}}} {{h_{m,n}}\left( {l - {\tau _{m,n}}} \right)u_q^n\left( {i - l} \right) + w_q^m\left( i \right),} \\ \;\;\;\;m = 1,2,\cdots ,{N_r},i = 0,1,\cdots M - 1 \end{array} $ | (3) |
如果ZP的长度K足够长,有K≥L+τm,n,那么式(3)可重新写为
| $ \begin{array}{l} y_q^m\left( i \right) = \sum\limits_{n = 1}^{{N_t}} {{e^{j2\pi {f_n}\left( {i + qM} \right)/N}}} \sum\limits_{l = 0}^K {{{\tilde h}_{m,n}}\left( l \right)u_q^n\left( {i - l} \right) + w_q^m\left( i \right),} \\ \;\;\;\;\;m = 1,\cdots ,{N_r},i = 0,1,\cdots M - 1 \end{array} $ | (4) |
其中 $ {{\tilde h}_{m,n}}\left( l \right) = \left\{ \begin{array}{l} {h_{m,n}}\left( {l - {\tau _{m,n}}} \right),{\tau _{m,n}} < l < L + {\tau _{m,n}}\\ 0,\;\;\;\;l < {\tau _{m,n}}或l > L + {\tau _{m,n}} \end{array} \right. $ 可以看出,$ {{\tilde h}_{m,n}}\left( l \right) $为系统的有效信道响应,时延包括在信道内. 下面将频偏包括在信道和信号中,定义 $ {{\hat h}_{m,n}}\left( l \right) = {e^{j\frac{{2\pi {f_n}l}}{N}}}{{\tilde h}_{m,n}}\left( l \right) $和 $ \hat u_q^n\left( l \right) = {e^{j\frac{{2\pi {f_n}\left( {i + qM} \right)}}{N}}}u_q^n\left( l \right) $,则可把式(4)转化为
| $ \begin{array}{l} y_q^m\left( i \right) = \sum\limits_{n = 1}^{{N_t}} {\sum\limits_{l = 0}^K {{{\hat h}_{m,n}}\left( l \right)\hat u_q^n} } \left( {i - 1} \right) + w_q^m\left( i \right),\\ m = 1,\cdots ,{N_r},i = 0,1,\cdots ,M - 1 \end{array} $ | (5) |
从式(5)可以看出,频偏包括在信道和发送符号中. 为了方便盲源分离,将式(5)写成矩阵形式为
| $ {y_q} = \hat H{{\hat u}_q} + {w_q},q = 0,1,\cdots $ | (6) |
其中 $ {\hat H}$为整体信道矩阵,含有待估频偏,为一个NrM×NtN维的Toeplitz矩阵,有
| $ \hat H = \left[{\begin{array}{*{20}{c}} {\hat h\left( {\rm{0}} \right)}&{\rm{0}}& \cdots &{\rm{0}}\\ \vdots &{\hat h\left( {\rm{0}} \right)}&{}& \vdots \\ {\hat h\left( K \right)}& \vdots &{}&{}\\ 0&{\hat h}& \cdots &0\\ {}&{}&{}&{\hat h\left( 0 \right)}\\ \vdots &{}&{}& \vdots \\ 0& \cdots &0&{\hat h} \end{array}} \right] $ | (7) |
定义 $ \hat P{\rm{ = }}{\left[{\hat h\left( 0 \right)\;\;\;\hat h\left( 1 \right)\;\;\; \cdots \;\;\;\hat h\left( K \right)} \right]^T} $,其中
| $ \hat h\left( l \right) = \left[{\begin{array}{*{20}{c}} {{{\hat h}_{1,1}}\left( l \right)}&{{{\hat h}_{1,2}}\left( l \right)}& \cdots &{{{\hat h}_{1,{N_t}}}\left( l \right)}\\ {{{\hat h}_{2,1}}\left( l \right)}&{{{\hat h}_{2,2}}\left( l \right)}& \cdots &{{{\hat h}_{2,{N_t}}}\left( l \right)}\\ \vdots & \vdots &{}& \vdots \\ {{{\hat h}_{{N_r},1}}\left( l \right)}&{{{\hat h}_{{N_r},2}}\left( l \right)}& \cdots &{{{\hat h}_{{N_r},{N_t}}}\left( l \right)} \end{array}} \right] $ | (8) |
为所有发射天线对所有接收天线上的第l径信道的响应系数. 含有频偏的信号为 $ {{\hat u}_q} = {[\hat u_q^1\left( 0 \right) \cdots \hat u_q^{{N_t}}\left( 0 \right)u \cdots \hat u_q^0\left( {N - 1} \right) \cdots \hat u_q^{{N_t}}\left( {N - 1} \right) \cdots \hat u_q^{{N_t}}\left( {N - 1} \right)]^T} $ 噪声为 $ {w_q} = {\left[{w_q^1\left( 0 \right) \cdots w_q^{{N_r}}\left( 0 \right) \cdots w_q^1\left( {M - 1} \right) \cdots w_q^{{N_r}}\left( {M - 1} \right)} \right]^T} $
2 基于盲解卷积的多频偏盲估计算法根据第1节建立的分布式MIMO-OFDM系统信号模型,给出多频偏盲估计算法.
2.1 卷积混合盲源分离若要使得盲解卷积问题可解,需要令接收天线个数大于发送天线个数(Nr≥Nt),同时要求噪声为白噪声且接收天线间的噪声互不相关,噪声和发送信号之间也不相关.
1) 计算接收信号的自相关
| $ {R_{{y_q}}} = E\left( {{y_q}y_q^H} \right) \approx \frac{1}{{{N_s}}}\sum\limits_{q = 1}^{{N_s}} {{y_q}y_q^H} $ | (9) |
这里需要在多个符号块上对自相关进行平均,其中Ns为发送的符号块数.
2) 计算噪声子空间
对自相关函数Ryq进行特征值分解,找到r=MNr-NNt个最小特征值,并求相应的特征向量gk,k=1,2,…,r,构成噪声子空间. 注意到gk为MNr×1维向量,将其划分为
| $ {g_k} = {\left[{\tilde g_k^T\left( 0 \right),\tilde g_k^T\left( 1 \right),\cdots ,\tilde g_k^T\left( {M - 1} \right)} \right]^T} $ | (10) |
其中 ${{\tilde g}_k}$(m),m=0,1,…,M-1为Nr×1维向量.
3) 整体信道矩阵 ${\hat P}$ 的估计
将噪声子空间的特征向量gk,k=1,2,…,r组合成一个新的矩阵为
| $ G = \sum\limits_{k = 0}^{r - 1} {G_k^H{G_k}} $ | (11) |
其中
| $ {G_k} = \left[{\begin{array}{*{20}{c}} {\tilde g_k^H\left( K \right)}&{\tilde g_k^H\left( {K - 1} \right)}& \cdots &{\tilde g_k^H\left( 0 \right)}\\ {\tilde g_k^H\left( {K + 1} \right)}&{\tilde g_k^H\left( K \right)}& \cdots &{\tilde g_k^H\left( 1 \right)}\\ \vdots & \vdots &{}& \vdots \\ {\tilde g_k^H\left( {M - 1} \right)}&{\tilde g_k^H\left( {M - 2} \right)}& \cdots &{\tilde g_k^H\left( {N - 1} \right)} \end{array}} \right] $ | (12) |
对G进行特征值分解,求得Nt个最小特征值,并得到对应的特征向量,构成整体信道矩阵 $ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\hat{H}}} $. $ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\hat{H}}} $为具有模糊度的 $ {\hat P} $ ,即 $ \hat{P}=\bar{\hat{P}}b,b $,为一个Nt×Nt的可逆矩阵.
4) 得到解卷积后的信号
将步骤3)中得到的整体信道矩阵$ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\hat{H}}} $按照式(7)的形式进行组合,得到具有模糊度的 ${\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\hat{H}}}$. 利用最小二乘法,求得发送信号为
| $ {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\hat{u}}}}_{q}}={{\left( \hat{H}\left\| ^{H}\left. {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\hat{H}}} \right\| \right. \right)}^{-1}}{{\left. {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\hat{H}}} \right\|}^{H}}{{y}_{q}} $ | (13) |
得到第q个OFDM符号块的信号为
| $ {{{\bar{\hat{r}}}}_{q}}={{[\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\hat{u}}_{q,}^{1}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\hat{u}}_{q}^{2},\cdots ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\hat{u}}_{q}^{{{N}_{t}}}]}^{T}} $ | (14) |
其中: $ {{{\bar{\hat{r}}}}_{q}}={{[\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\hat{u}}_{q}^{n}\left( 0 \right),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\hat{u}}_{q}^{n}\left( 1 \right),\cdots ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\hat{u}}_{q}^{n}\left( N-1 \right)]}^{T}};$ $ {{{\bar{\hat{r}}}}_{q}} $为Nt×N维矩阵,每一行即为所求的发送信号,共Nt个. 但此时信号还具有线性模糊度,利用线性分离方法可得到没有模糊度的信号 $ {{\hat r}_q} $,此时的信号只含有频偏和噪声. 因此,可对 $ \hat u_q^n $进行频偏估计,得到频偏fn,n=1,2,…,Nt.
2.2 频偏盲估计分离出的 $ \hat u_q^n $为OFDM信号,进行傅里叶变换(FFT,fast Fourier transform)后,得到OFDM解调后的信号 $ \hat U_q^n $. 利用文献[7]中的式(29),可得
| $ {{\hat f}_n} = \frac{1}{M}\mathop {{\mathop{\rm argmax}\nolimits} }\limits_{\left| {{{\bar f}_0}} \right| < \frac{1}{2}} \frac{1}{N}\left| {\sum\limits_{k = 0}^{N - 1} {{{\left( {\hat U_q^n} \right)}^4}{e^{ - j2\pi {{\bar f}_0}k/N}}} } \right| $ | (15) |
其中:M为信号的调制指数,这里采用正交相移键控(QPSK,quadrature phase shift keyin)调制; $ {{\bar f}_0} $为待搜索频偏,范围在[-0.5,0.5]. 依次对Nt个信号进行处理,可得频偏估计值 $ {{\hat f}_n} $,n=1,2,…,Nt.
3 仿真结果与性能分析为了验证上述理论分析的正确性和算法估计的精确度,同时借鉴文献[5]对实验的设计,笔者将从算法性能与接收天线数、OFDM符号数的关系和与现有算法的对比这3个方面进行仿真实验.
实验1 考察不同用户的频偏估计性能随接收天线数变化的情况,如 图 2所示. 发射天线数Nt=2,接收天线数Nr=2,3,4,5,6. 每个OFDM符号块有N=128点子载波,ZP长度K为8. OFDM符号数为800. 采用6径(L=6)的多径信道,信道系数采用均值为0,方差为1的随机高斯变量,归一化频偏(对子载波间隔归一化)分别为0.010,0.015.
由 图 2可以看出,当接收天线数Nr大于发射天线数时,随着接收天线数的增加,估计性能逐步提高,在信噪比为5dB时能达到较高的估计精度. 这是由于接收天线数增加,盲源分离效果更加显著,天线间的干扰被减小,对频偏估计性能的影响变弱. 当接收天线数为5和6时,估计性能趋于稳定.
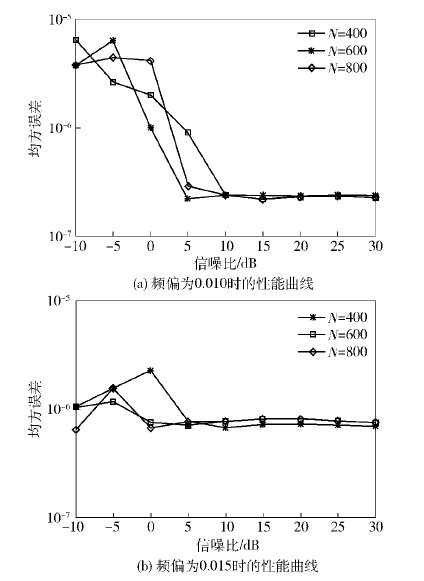
实验2 考察不同用户的频偏估计性能随OFDM符号数变化的结果,如 图 3所示. 接收天线数Nr=5,OFDM符号数分别为400、600、800. 其他仿真条件同实验1.
由 图 3可以看出,当符号数从400增加到600,低信噪比(5dB以下)时的频偏估计性能提升较为显著. 当符号数从600增加到800,估计性能在低信噪比时有一定起伏,但整体趋势是一样的,性能差异不大,即随着符号数的增加并不能显著提高估计性能. 因此,符号数为600时即可有效估计出所有频偏.
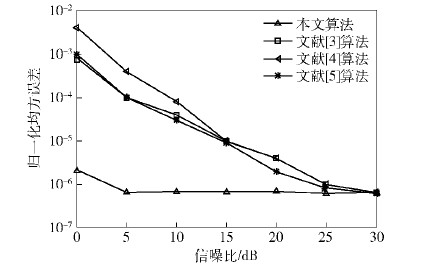
实验3 与现有算法进行对比(见 图 4). 接收天线数为5,OFDM符号数为600,这里对频偏估计的归一化均方误差进行对比,其余仿真条件同上. 在现有算法中,选取基于交替空间广义期望最大化(SAGE,space-alternating generalized expectation-maximization)的算法[3, 4]以及盲估计方法[5].
由 图 4可以看出,在整个信噪比范围内,笔者所提算法性能都优于文献中的算法性能. 同时,笔者所提算法在信噪比为5dB时,性能即趋于稳定. 与现有算法相比,笔者所提算法针对低信噪比、多径信道环境和OFDM信号时具有良好的频偏盲估计性能.
4 结束语笔者提出了一种针对多径衰落信道下分布式OFDM系统的多频偏盲估计算法. 引入盲源分离理论中的去解卷积思想,去除了接收信号中的多径信道影响,进而得到了对频偏的估计. 仿真结果表明,所提算法可以在接收天线数和符号数较少、频偏值比较接近的情况下,实现对多频偏的盲估计.
| [1] | 刘辉. 分布式MIMO-OFDM系统的多载波频偏估计[D]. 哈尔滨: 哈尔滨工业大学, 2010.[引用本文:1] |
| [2] | Yao Yao, Tunasang N. Correlation-based frequency offset estimation in MIMO system[C]//Vehicular Technology Conference. Florida: IEEE, 2003: 438-442.[引用本文:1] |
| [3] | Thehanh P, Nallanathan A, Liang Yingchang. Joint channel and frequency offset estimation in distributed MIMO flat-fading channels[J]. IEEE Transactions on Wireless Communications, 2008, 7(2): 648-656.[引用本文:2] |
| [4] | Tian Yuan, Lei Xia, Xiao Yue, et al. SAGE based joint timing-frequency offsets and channel estimation in distributed MIMO systems[J]. Computer Communications, 2010, 33(17): 2125-2131.[引用本文:2] |
| [5] | Nasir A A, Durrani S, Kennedy R A. Blind timing and carrier synchronisation in distributed multiple input multiple output communication systems[J]. IET Communications, 2011, 5(7): 1028-1037.[引用本文:3] |
| [6] | 付卫红, 杨小牛, 刘乃安, 等. 基于子空间分解的多通道盲解卷积算法[J]. 通信学报, 2009, 30(1): 25-30. Fu Weihong, Yang Xiaoniu, Liu Naian, et al. Algorithm for multichannel blind deconvolution based on subspace decomposition[J]. Journal on Communications, 2009, 30(1): 25-30.[引用本文:1] |
| [7] | Wang Yan, Serpedin E, Ciblat P. Optimal blind carrier recovery for MPSK burst transmissions[J]. IEEE Transactions on Communications, 2003, 51(9): 1571-1581.[引用本文:1] |