2. 河南理工大学 机械与动力工程学院, 河南 焦作 454000
提出Stephenson-Ⅲ型平面六杆机构五精确点轨迹综合代数求解方法.将Stephenson-Ⅲ型平面六杆机构拆分为一个二级杆组和一个四杆机构,先对二级杆组五精确点综合,再对四杆机构进行精确点综合. 采用矩阵约束法建立该问题的数学模型,使用Groebner基和Sylvester结式(GS法)相结合的代数方法进行求解,最终获得一元高次方程及其全部封闭解析解. 通过数值实例,并使用Solidworks和SAM软件对计算结果进行仿真,结果表明该方法的正确性. 该方法为进一步采用代数法对其他类型平面六杆机构轨迹综合问题的研究提供了参考.
2. School of Mechanical and Power Engineering, Henan Polytechnic University, Henan Jiaozuo 454000, China
An algebraic solution for five precision points path synthesis of Stephenson-Ⅲ planar six-bar linkage was presented. The Stephenson-Ⅲ planar six-bar linkage is decomposed into two parts: a dyad and a four-bar linkage. To synthesize the two parts, the dyad first then the four-bar linkage, the kinematic constraint equations are formulated based on displacement matrix. The equations are solved with the Groebner-Sylvester (GS) hybrid approach in which a high degree univariate equation together with all its closed form solution is obtained finally. A numerical example was provided to validate the algorithm and the solutions are verified by Solidworks and SAM. The method given in this article can also be used to solve other types of synthesis problem concerning planar six-bar linkage.
平面六杆机构是机械中常用的一种多杆机构,其轨迹综合问题可分为近似轨迹综合和精确点轨迹综合,求解方法分为数值优化法和代数解析法. 目前,对轨迹综合问题的研究[1, 2, 3],大多数集中于近似轨迹综合,主要采用优化综合方法研究. 而对精确点轨迹综合问题,鲜有学者进行研究[4],究其原因,主要是由于建立的综合方程本质是非线性方程组,且其代数结构通常较复杂,而目前非线性方程组的代数求解方法由于不同方面的局限性使得该方面研究进展缓慢. 笔者以Stephenson-Ⅲ型平面六杆机构为对象,使用分次逆字典序Groebner基和Sylvester结式相结合的代数方法研究五精确点轨迹综合问题. 使用Solidworks和SAM软件对数据进行仿真,验证了结果的正确性.
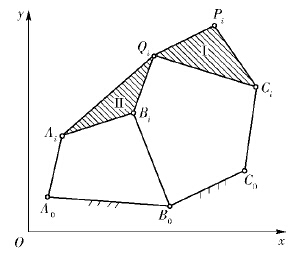
1 数学模型图 1是Stephenson-Ⅲ型平面六杆机构. 该机构有2个浮动杆(连杆),以Δθi=θi-θ1表示浮动杆I的转角,以Δδi=δi-δ1表示浮动杆II的转角(i=2,…,n,其中n是精确点个数). 以Pi点和Qi点分别作为这2个浮动杆的基点,A0、B0和C0为固定铰链点,Ai、Bi和Ci为活动铰链点. 精确点轨迹综合就是求解连杆机构的尺寸并确保六杆机构在运动过程中点Pi精确地通过平面上给定的n个点.
为描述方便,如图 1所示任意建立参考坐标系xOy,设固定铰链点A0、B0和C0的坐标为(a0x,a0y)、(b0x,b0y)和(c0x,c0y),活动铰链点Ai、Bi、Ci和基点Qi、Pi在第i个位置坐标为(aix,aiy)、(bix,biy)、(cix,ciy)、(qix,qiy)和(pix,piy)(i=1,2,…,n). 根据平面刚体转移矩阵,Ci和Qi的坐标为
| $\begin{gathered} amp;\left[ \begin{gathered} amp;{c_{ix}} \hfill \\ amp;{c_{iy}} \hfill \\ amp;1 \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} amp;\cos \left( {\Delta {\theta _i}} \right){\text{ }} - \sin \left( {\Delta {\theta _i}} \right){\text{ }}{P_{ix}} - {P_{1x}}\cos \left( {\Delta {\theta _i}} \right) + {P_{1y}}\sin \left( {\Delta {\theta _i}} \right) \hfill \\ amp;\sin \left( {\Delta {\theta _i}} \right){\text{ }}\cos \left( {\Delta {\theta _i}} \right){\text{ }}{P_{iy}} - {P_{1x}}\sin \left( {\Delta {\theta _i}} \right) + {P_{1y}}cos\left( {\Delta {\theta _i}} \right){\text{ }} \hfill \\ amp;{\text{ }}0{\text{ }}0{\text{ }}1 \hfill \\ \end{gathered} \right] \hfill \\ amp;\left[ \begin{gathered} amp;{c_{1x}} \hfill \\ amp;{c_{1y}} \hfill \\ amp;1 \hfill \\ \end{gathered} \right],i = 2, \cdots ,n \hfill \\ \end{gathered} $ | (1) |
| $\begin{gathered} amp;\left[ \begin{gathered} amp;{q_{ix}} \hfill \\ amp;{q_{iy}} \hfill \\ amp;1 \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} amp;\cos \left( {\Delta {\theta _i}} \right){\text{ }} - \sin \left( {\Delta {\theta _i}} \right){\text{ }}{P_{ix}} - {P_{1x}}\cos \left( {\Delta {\theta _i}} \right) + {P_{1y}}\sin \left( {\Delta {\theta _i}} \right) \hfill \\ amp;\sin \left( {\Delta {\theta _i}} \right){\text{ }}\cos \left( {\Delta {\theta _i}} \right){\text{ }}{P_{iy}} - {P_{1x}}\sin \left( {\Delta {\theta _i}} \right) + {P_{1y}}cos\left( {\Delta {\theta _i}} \right){\text{ }} \hfill \\ amp;{\text{ }}0{\text{ }}0{\text{ }}1 \hfill \\ \end{gathered} \right] \hfill \\ amp;\left[ \begin{gathered} amp;{q_{1x}} \hfill \\ amp;{q_{1y}} \hfill \\ amp;1 \hfill \\ \end{gathered} \right],i = 2, \cdots ,n \hfill \\ \end{gathered} $ | (2) |
因为Ci绕C0旋转,受定长约束条件有
| ${{\left( {{C}_{i}}-{{C}_{0}} \right)}^{T}}\left( {{C}_{i}}-{{C}_{0}} \right)-{{\left( {{C}_{i}}-{{C}_{0}} \right)}^{T}}\left( {{C}_{i}}-{{C}_{0}} \right)=0,i=2,\cdots ,n$ | (3) |
同理Ai和Bi的坐标为
| $\begin{gathered} amp;\left[ \begin{gathered} amp;{a_{ix}} \hfill \\ amp;{a_{iy}} \hfill \\ amp;1 \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} amp;\cos \left( {\Delta {\delta _i}} \right){\text{ }} - \sin \left( {\Delta {\delta _i}} \right){\text{ }}{q_{ix}} - {q_{1x}}\cos \left( {\Delta {\delta _i}} \right) + {q_{1y}}\sin \left( {\Delta {\delta _i}} \right) \hfill \\ amp;\sin \left( {\Delta {\delta _i}} \right){\text{ }}\cos \left( {\Delta {\delta _i}} \right){\text{ }}{q_{iy}} - {q_{1x}}\sin \left( {\Delta {\delta _i}} \right) + {q_{1y}}cos\left( {\Delta {\delta _i}} \right){\text{ }} \hfill \\ amp;{\text{ }}0{\text{ }}0{\text{ }}1 \hfill \\ \end{gathered} \right] \hfill \\ amp;\left[ \begin{gathered} amp;{a_{1x}} \hfill \\ amp;{a_{1y}} \hfill \\ amp;1 \hfill \\ \end{gathered} \right],i = 2, \cdots ,n \hfill \\ \end{gathered} $ | (4) |
| $\begin{gathered} amp;\left[ \begin{gathered} amp;{b_{ix}} \hfill \\ amp;{b_{iy}} \hfill \\ amp;1 \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} amp;\cos \left( {\Delta {\delta _i}} \right){\text{ }} - \sin \left( {\Delta {\delta _i}} \right){\text{ }}{q_{ix}} - {q_{1x}}\cos \left( {\Delta {\delta _i}} \right) + {q_{1y}}\sin \left( {\Delta {\delta _i}} \right) \hfill \\ amp;\sin \left( {\Delta {\delta _i}} \right){\text{ }}\cos \left( {\Delta {\delta _i}} \right){\text{ }}{q_{iy}} - {q_{1x}}\sin \left( {\Delta {\delta _i}} \right) + {q_{1y}}cos\left( {\Delta {\delta _i}} \right){\text{ }} \hfill \\ amp;{\text{ }}0{\text{ }}0{\text{ }}1 \hfill \\ \end{gathered} \right] \hfill \\ amp;\left[ \begin{gathered} amp;{b_{1x}} \hfill \\ amp;{b_{1y}} \hfill \\ amp;1 \hfill \\ \end{gathered} \right],i = 2, \cdots ,n \hfill \\ \end{gathered} $ | (5) |
受定长约束条件有
| ${{\left( {{A}_{i}}-{{A}_{0}} \right)}^{T}}\left( {{A}_{i}}-{{A}_{0}} \right)-{{\left( {{A}_{i}}-{{A}_{0}} \right)}^{T}}\left( {{A}_{i}}-{{A}_{0}} \right)=0,i=2,\cdots ,n$ | (6) |
| ${{\left( {{B}_{i}}-{{B}_{0}} \right)}^{T}}\left( {{B}_{i}}-{{B}_{0}} \right)-{{\left( {{B}_{i}}-{{B}_{0}} \right)}^{T}}\left( {{B}_{i}}-{{B}_{0}} \right)=0,i=2,\cdots ,n$ | (7) |
方程组(3)、(6)和(7)总共含有3(n-1)个方程式,其中含有2n+12个变量,即A0、B0、C0、A1、B1、C1、θi和δi(i=1,2,…,n)(每个矢量含2个标量). 根据方程式个数与变量个数必须相等的原则,可知Stephenson-Ⅲ型平面六杆机构轨迹综合的精确点个数最大为15. 通常要综合的精确点个数越多,所涉及的非线性方程组结构越复杂,代数求解十分困难. 笔者主要研究五精确点的轨迹综合代数法求解问题.
令cθi=cos(Δθi),sθi=sin(Δθi),将式(1)代入式(3),并展开得
| $c\theta _{i}^{2}+s\theta _{i}^{2}=1,i=2,\cdots ,5$ | (8) |
| ${{\alpha }_{i1}}c{{\theta }_{i}}+{{\alpha }_{i2}}s{{\theta }_{i}}+{{\alpha }_{i3}}=0,i=2,\cdots ,5$ | (9) |
| $\begin{align} & {{\alpha }_{i1}}=-{{c}_{0x}}{{c}_{1x}}-{{c}_{0y}}{{p}_{1y}}+{{c}_{0x}}{{p}_{1x}}+{{c}_{0y}}{{p}_{1y}}+{{c}_{1x}}{{p}_{ix}}- \\ & {{p}_{1x}}{{p}_{ix}}+{{c}_{1y}}{{p}_{iy}}-{{p}_{1y}}{{p}_{iy}} \\ & {{\alpha }_{i2}}=-{{c}_{0y}}{{c}_{1x}}+{{c}_{0x}}{{c}_{1y}}+{{c}_{0y}}{{p}_{1x}}+{{c}_{0x}}{{p}_{1y}}+{{c}_{1y}}{{p}_{ix}}- \\ & {{p}_{1y}}{{p}_{ix}}+{{c}_{1x}}{{p}_{iy}}-{{p}_{1x}}{{p}_{iy}} \\ & {{\alpha }_{i3}}=-{{c}_{0x}}{{c}_{1x}}+{{c}_{0y}}{{c}_{1y}}-{{c}_{1x}}{{p}_{1x}}-{{c}_{1y}}{{p}_{1y}}-{{c}_{0x}}{{p}_{ix}}- \\ & {{c}_{0y}}{{p}_{iy}}+\frac{1}{2}\left( p_{1x}^{2}+p_{1y}^{2}+p_{ix}^{2}+p_{iy}^{2} \right) \\ \end{align}$ |
令cδi=cos(Δδi),sδi=sin(Δδi),将式(2)、式(4)、式(5)代入式(6)和式(7),并展开得
| $c\delta _{i}^{2}+s\delta _{i}^{2}=1,i=2,\cdots ,5$ | (10) |
| ${{\beta }_{i1}}c{{\delta }_{i}}+{{\beta }_{i2}}s{{\delta }_{i}}+{{\beta }_{i3}}=0,i=2,\cdots ,5$ | (11) |
| ${{\eta }_{i1}}c{{\delta }_{i}}+{{\eta }_{i2}}s{{\delta }_{i}}+{{\eta }_{i3}}=0,i=2,\cdots ,5$ | (12) |
| $\begin{align} & {{\beta }_{i1}}=-{{a}_{0x}}{{a}_{1x}}-{{a}_{0y}}{{a}_{1y}}+{{a}_{0x}}{{q}_{1x}}+{{a}_{0y}}{{q}_{1y}}+{{a}_{1x}}{{q}_{ix}}- \\ & {{q}_{1x}}{{q}_{ix}}+{{a}_{1y}}{{q}_{iy}}-{{q}_{1y}}{{q}_{iy}} \\ & {{\beta }_{i2}}=-{{a}_{0y}}{{a}_{1x}}+{{a}_{0x}}{{a}_{1y}}+{{a}_{0y}}{{q}_{1x}}+{{a}_{0x}}{{q}_{1y}}+{{a}_{1y}}{{q}_{ix}}+ \\ & {{a}_{1x}}{{q}_{iy}}-{{q}_{1x}}{{q}_{iy}} \\ & {{\beta }_{i3}}=-{{a}_{0x}}{{a}_{1x}}+{{a}_{0y}}{{a}_{1y}}-{{a}_{1x}}{{q}_{1x}}-{{a}_{1y}}{{q}_{1y}}-{{a}_{0x}}{{q}_{ix}}+ \\ & \frac{1}{2}\left( q_{1x}^{2}+q_{1y}^{2}+q_{ix}^{2}+q_{iy}^{2} \right) \\ \end{align}$ |
| $\begin{align} & {{\eta }_{i1}}=-{{b}_{0x}}{{b}_{1x}}-{{b}_{0y}}{{b}_{1y}}+{{b}_{0x}}{{q}_{1x}}+{{b}_{0y}}{{q}_{1y}}+{{b}_{1x}}{{q}_{ix}}- \\ & {{q}_{1x}}{{q}_{ix}}+{{b}_{1y}}{{q}_{iy}}-{{q}_{1y}}{{q}_{iy}} \\ & {{\eta }_{i2}}=-{{b}_{0y}}{{b}_{1x}}+{{b}_{0x}}{{b}_{1y}}+{{b}_{0y}}{{q}_{1x}}-{{b}_{0x}}{{q}_{1y}}-{{b}_{1y}}{{q}_{ix}}+{{q}_{1y}}{{q}_{ix}}+ \\ & {{b}_{1x}}{{q}_{iy}}-{{q}_{1x}}{{q}_{iy}} \\ & {{\eta }_{i3}}=-{{b}_{0x}}{{b}_{1x}}+{{b}_{0y}}{{b}_{1y}}-{{b}_{1x}}{{q}_{1x}}-{{b}_{1y}}{{q}_{1y}}-{{b}_{0x}}{{q}_{ix}}-{{b}_{0y}}{{q}_{iy}}+ \\ & \frac{1}{2}\left( q_{1x}^{2}+q_{1y}^{2}+q_{ix}^{2}+q_{iy}^{2} \right) \\ \end{align}$ |
式(8)~式(12)共20个方程为Stephenson-Ⅲ型平面六杆机构五精确点轨迹综合的数学模型. 假设a0x,a0y,b0x,b0y,c0x,c0y,c1x,c1y,q1x,q1y为已知变量,其他20个待求变量为a1x,a1y,b1x,b1y,cθi,sθi,cδi,sδi (i=2,…,5). 按照所给参数,综合过程中可将该机构拆分为一个二级杆组C0Ci和一个四杆机构A0A1B1B0,综合问题就变为先根据精确点Pi的5个位置对C0Ci综合求出基点Qi的5个精确位置,然后再对A0A1B1B0进行精确点轨迹综合.
2 消元与求解式(8)~式(12)为20元2次非线性多项式方程组,若直接应用常见的代数消元法,如Dixon结式法、Sylvester结式法、吴方法,难以得到求解. 笔者分2步求解:首先通过式(8)和式(9)求出cθi,sθi,并代入式(2)求出qix,qiy;然后求解式(10)~式(12)的分次逆字典序Groebner基,分析所生成基的变量以及由变量不同次幂组成的项,通过压缩合适的变量使基的个数与项的个数相等,构造Sylvester结式,进而得到一元高次方程式.
2.1 求解qix,qiy由式(8)和式(9)求解得
| $\left. \begin{align} & c{{\theta }_{i}}=-\frac{{{\alpha }_{i1}}{{\alpha }_{i3}}+{{\alpha }_{i2}}\sqrt{\alpha _{i1}^{2}+\alpha _{i2}^{2}+\alpha _{i3}^{3}}}{\alpha _{i1}^{2}+\alpha _{i2}^{2}} \\ & s{{\theta }_{i}}=-\frac{{{\alpha }_{i2}}{{\alpha }_{i3}}+{{\alpha }_{i1}}\sqrt{\alpha _{i1}^{2}+\alpha _{i2}^{2}+\alpha _{i3}^{3}}}{\alpha _{i1}^{2}+\alpha _{i2}^{2}} \\ \end{align} \right\}$ |
| $\left. \begin{align} & c{{\theta }_{i}}=\frac{-{{\alpha }_{i1}}{{\alpha }_{i3}}+{{\alpha }_{i2}}\sqrt{\alpha _{i1}^{2}+\alpha _{i2}^{2}+\alpha _{i3}^{3}}}{\alpha _{i1}^{2}+\alpha _{i2}^{2}} \\ & s{{\theta }_{i}}=-\frac{{{\alpha }_{i2}}{{\alpha }_{i3}}+{{\alpha }_{i1}}\sqrt{\alpha _{i1}^{2}+\alpha _{i2}^{2}+\alpha _{i3}^{3}}}{\alpha _{i1}^{2}+\alpha _{i2}^{2}} \\ & i=2,\cdots ,5 \\ \end{align} \right\}$ | (13) |
将式(13)的2组解分别代入式(2)可求出
| $\left. \begin{align} & {{q}_{ix}}={{p}_{ix}}+\left( {{q}_{1x}}-{{p}_{1x}} \right)c{{\theta }_{i}}-\left( {{p}_{1y}}-{{p}_{1y}} \right)s{{\theta }_{i}} \\ & {{q}_{iy}}={{p}_{iy}}+\left( {{q}_{1y}}-{{p}_{1y}} \right)c{{\theta }_{i}}+\left( {{q}_{1x}}-{{p}_{1x}} \right)s{{\theta }_{i}} \\ & i=2,\cdots ,5 \\ \end{align} \right\}$ | (14) |
分次逆字典序Groebner基的基本思想是在原多项式系统所构成的多项式环内,通过对变量多项式的适当排序,求多项式的S多项式,并通过约简,最后生成一个与原系统完全等价的标准基. 直接运用计算机代数系统Mathematica软件中提供的GroebnerBasis命令,以cδi,sδi,a1x,a1y,b1x,b1y (i=2,…,5)为变量,按照单项式的分次逆字典序排列cδ2>sδ2>cδ3>sδ3>cδ4>sδ4>cδ5>sδ5>a1x>a1y>b1x>b1y,计算式(10)~式(12)的分次逆字典序Groebner基,得到一个92个多项式方程的分次逆字典序Groebner基,将b1y作为压缩变量,取Groebner基中第56~78共23个多项式方程,写成矩阵形式为
| ${{M}_{23\times 23}}T=0$ | (15) |
其中:M23×23为一个关于b1y的23×23阶系数矩阵,T为一个含有23个假想变元的列阵,有
T=[1,a1x,a1y,a1xa1y,a21y,b1x,a1xb1x,a1yb1x,b21x,cδ2,cδ3,cδ4,cδ5,a1ycδ5,sδ2,b1xsδ2,sδ3,b1xsδ3,sδ4,b1xsδ4,sδ5,a1ysδ5,b1xsδ5]T
2.3 获取一元高次方程由代数学可知,方程组(15)有解的条件是其系数行列式等于0,即
| $\det \left( {{M}_{23\times 23}} \right)=0$ | (16) |
为准确得到解的数目,在展开行列式前判断方程的次数十分重要. 矩阵M23×23每列关于变量b1y的最高次数为3、2、2、1、1、2、1、1、1、2、2、2、2、1、2、1、2、1、2、1、2、1、1,其总和为36. 根据行列式的运算法则可知,展开式(16)后得到只含变量b1y的多项式最高次数不会超过36. 由式(16),不需要提取任何公因式,展开直接得到的关于变量b1y的一元36次输入输出方程
| $\sum\limits_{i=0}^{36}{{{s}_{i}}b_{1y}^{i}}=0$ | (17) |
由以上分析可知,构造的23阶单变量系数行列式与展开系数行列式后获得的一元多项式在符号形式上最高次数是完全一致的. 解式(17),将得到36个复数解.
2.4 求解其他变量将所求得的36个b1y值代入23个多项式中的任何22个式中,则这22个多项式变成除假想变元1之外的22个假想变元的线性方程组,解此方程组,可求得对应于b1y的a1x,a1y,b1x值. 根据式(13)的2组解,每组对应36组复数解,共72组复数解.
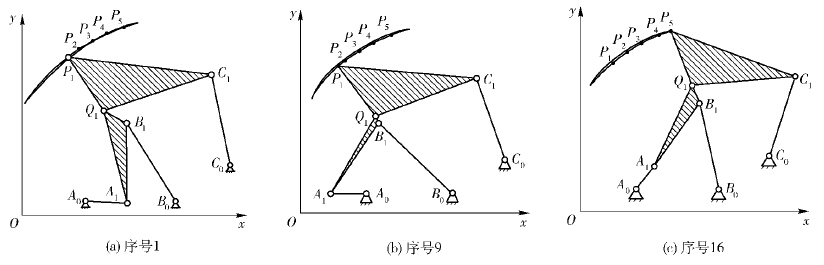
3 数值算例Stephenson-Ⅲ型的平面六杆机构已知参数如下:a0x=5.000 34、a0y=4.006 362、b0x=9.987 826、b0y=3.986 323、c0x=13.024 281、c0y=5.999 102、c1x=11.977 239、c1y=10.995 276、q1x=5.992 995、q1y=9.013 963、p1x=4、p1y=12、p2x=4.625、p2y=12.440、p3x=5.380、p3y=12.880、p4x=6.150、p4y=13.300、p5x=7.120、p5y=13.630. 根据上述步骤,可求得72组复数解,其中实数解为44组,如表1所示. 通过Solidworks和SAM[5]软件仿真,可以验证表1中的数据满足通过五精确点的轨迹要求,例如序号1、9、16的仿真结果如图 2所示.
| 表1 数值算例的44组实数解 |
4 结束语
根据已知参数可将Stephenson-Ⅲ型平面六杆机构的五精确点轨迹综合问题转化为求解一个二级杆组和一个四杆机构的轨迹综合问题. 采用分次逆字典序Groebner基和Sylvester结式结合的代数方法求解Stephenson-Ⅲ型平面六杆机构的五精确点轨迹综合问题,获得该问题的全部封闭形式的解析解. 求解过程中,不需要提取任何公因式,无增根且无漏根. 同时,使用Solidworks和SAM软件对数据进行验证,证明了该方法的有效性. 文中提供的新思路,为进一步采用代数法对其他类型的平面六杆机构轨迹综合问题研究提供了参考.
| [1] | Todorov T S. Synthesis of Watt's six-link mechanism for manipulation action in relative space[J]. Mechanism and Machine Theory, 1997, 32(5): 559-568.[引用本文:1] |
| [2] | Shiakolas P S, Koladiya D, Kebrle J. On the optimum synthesis of six-bar linkages using differential evolution and the geometric centroid of precision positions technique[J]. Mechanism and Machine Theory, 2005, 40(3): 319-335.[引用本文:1] |
| [3] | Mariappan J, Krishnamurty S. A generalized exact gradient method for mechanism synthesis[J]. Mechanism and Machine Theory, 1996, 31(4): 413-421.[引用本文:1] |
| [4] | Kim H S, Hamid S, Soni A H. Synthesis of six-link mechanisms for point path generation[J]. Journal of Mechanisms, 1972, 6(4): 447-461.[引用本文:1] |
| [5] | Creaktor S. The SAM software homepage [EB/OL]. USA: The Artas Enginering Software, 2015[2015-03-26]. http://www.artas.nl.[引用本文:1] |