2. 北京邮电大学 安全生产智能监控北京市重点实验室, 北京 100876
针对多路传输控制协议联合拥塞控制未考虑丢包率对吞吐量的影响和传统静态路径选择方法降低并行数据传输鲁棒性的问题,提出一种以提升吞吐量为优化目标的基于马尔可夫决策过程的动态路径选择方法. 综合考虑往返时延和丢包率对吞吐量的影响,根据最优策略动态地选取不同的路径进行数据传输,数据传输时不减少路径数量,在不影响并行数据传输鲁棒性的基础上提升吞吐量. 仿真结果表明,在路径参数变化时,所提出的路径选择方法可以更有效地均衡流量,提升吞吐量.
2. Beijing Key Laboratory of Work Safety Intelligent Monitoring, Beijing University of Posts and Telecommunications, Beijing 100876, China
To solve the problem that the coupled congestion control mechanism of multipath transmission control protocol (MPTCP) did consider the impact of loss rate to the throughput and the traditional static path selection methods did decrease the robustness of parallel data transmission, a dynamic MPTCP path selection method with improving throughput as an optimization target based on Markov decision processes was proposed. This method takes into account the impact of both round trip time and packet loss rate to throughput, chooses different paths based on optimal policy to transfer data but not reduce the number of paths so that it promotes the throughput without reducing the robustness of the parallel data transmission. Simulation shows that the proposed path selection method balances the data stream more effectively and improves the throughput of MPTCP.
随着互联网和网络接入技术的发展,越来越多的设备装配有多个网络接口(以太网、WiFi和3G/4G等). 标准的TCP/IP协议并不支持多个接口并行传输,这不仅对硬件接口和网络带宽造成了资源上的浪费,而且带来了较差的用户体验. 针对如何使用多个网络接口进行多路并行数据传输(CMT,concurrent multipath transfer)的问题,目前已经有了比较多的研究. 这些研究集中在应用层[1]、传输层[2]和网络层[3]. 多路传输控制协议(MPTCP,multipath transmission control protocol)是一种对标准TCP协议扩展[4]的传输层并行数据传输协议.
MPTCP通过联合拥塞控制[5]来解决TCP公平性问题,均衡各子流的数据传输[6]. 但联合拥塞控制在均衡数据流量时未考虑丢包率对吞吐量的影响,在丢包率较大的网络环境中不能有效地均衡流量. 在并行数据传输中由于各条路径的参数不同,不合理的路径选择会影响其传输性能[7]. 但传统的静态路径选择方法会减少传输路径的数量,降低并行数据传输的鲁棒性.
针对联合拥塞控制未考虑丢包率对吞吐量的影响和传统静态路径选择方法降低并行数据传输鲁棒性的问题,笔者在MPTCP联合拥塞控制的马尔可夫模型[8]基础上提出一种基于马尔可夫决策过程的MPTCP动态路径选择方法. 该方法依据各路径窗口大小动态地选择路径,在数据发送时根据最优策略选用不同的路径进行传输,综合考虑了往返时延和丢包率对吞吐量的影响,可以更加有效地均衡流量;在数据传输中同时使用所有路径进行数据传输,不会影响并行数据传输的鲁棒性,在保证并行传输鲁棒性的基础上提升了吞吐量.
1 动态路径选择模型建立基于马尔可夫决策过程的动态路径选择模型需要确定马尔可夫决策过程的四重组{S,A(i),P(j|i,a),R(i,a),i,j∈S,a∈A(i)},其中S为状态集,A(i)表示状态为i时可采取的行动集,P(j|i,a)表示状态为i时采取行动a后状态转移到j的概率,R(i,a)表示状态为i时采取行动a后得到的反馈.
1.1 模型建立从马尔可夫决策过程四重组出发构建基于马尔可夫决策过程的动态路径选择模型. 假设共有n条路径,n条路径的往返时延、丢包率和最大窗口分别为Tk、pk和Wk,其中k=1,2,…,n.
1) 状态集S
MPTCP各个路径的拥塞窗口具有马尔可夫性,下一时刻的窗口大小只与当前时刻的窗口大小有关,选择各条路径的拥塞窗口组成状态集S.
| $ \begin{array}{*{20}{c}} {S = \left\{ {\left( {c{w_1},c{w_2}, \cdots ,c{w_n}} \right)\left| {c{w_k} \in \left[ {1,{W_k}} \right]} \right.} \right.,}\\ {\left. {k = 1,2, \cdots ,n} \right\}} \end{array} $ | (1) |
2) 行动集A(i)
行动表示不同的路径选择策略,n条路径共有2n-1种策略. 令Atotal表示所有行动的集合,Atotal={a1,a2,…,a2n-1};令Rm表示路径选择策略am所包含的所有路径,m=1,2,…,2n-1;令R表示所有的n条路径. 联合拥塞控制的一个重要目标就是保证数据并行传输过程中的TCP公平性,在基于马尔可夫决策过程的路径选择模型中存在由少路径数量切换到多路径数量的情况. 在这种情况下,如果行动集合为Atotal,则可能出现并行传输吞吐量大于最大单路径传输吞吐量的情况,所以状态i时所选择的策略要满足其吞吐量不大于最大单路径传输吞吐量,即A(i)={am|am∈Atotal且Rm满足式(2)},其中cwki表示在状态i时路径k的窗口大小.
| $ \sum\limits_{k \in {R_m}} {\frac{{cw_k^i}}{{{T_k}}}} \le \mathop {\max }\limits_{k \in R} \frac{{{W_k}}}{{{T_k}}} $ | (2) |
3) 状态转移概率P(j|i,a)
根据MPTCP的联合拥塞控制机制[5],在使用行动am时的拥塞控制可表示为:
① 在路径k上每收到一个应答包,路径k的拥塞窗口cwk就增加min(am/cwtotal,1/cwk);
② 在路径k上一旦发生丢包,路径k的拥塞窗口cwk就减小到cwk/2.
| $ {a_m} = c{w_{{\rm{total}}}}\frac{{\mathop {\max }\limits_{k \in {R_m}} c{w_k}/T_k^2}}{{{{\left( {\sum\limits_{k \in {R_m}} {c{w_k}/{T_k}} } \right)}^2}}} $ | (3) |
假设在使用行动am后,路径k(k∈Rm)经过cntkm个分组后窗口增加1. 路径k窗口的变化有2种可能,窗口cwk增加1或是减半,其概率如式(5)所示. 则从状态i变化到状态j的状态转移概率P(j|i,am)可表示为式(6)所示的形式.
| $ cnt_k^m = \max \left( {\frac{{c{w_{{\rm{total}}}}}}{{{a_m}}},c{w_k}} \right) $ | (4) |
| $ f\left( {{p_k},{\rm{cnt}}_k^m} \right) = \left\{ \begin{array}{l} {\left( {1 - {p_k}} \right)^{{\rm{cnt}}_k^m}},\;\;\;c{w_k}加1\\ 1 - {\left( {1 - {p_k}} \right)^{{\rm{cnt}}_k^m}},\;\;\;c{w_k}减半 \end{array} \right. $ | (5) |
| $ P\left( {j|i,{a_m}} \right) = \prod\limits_{k \in {R_m}} {f\left( {{p_k},{\rm{cnt}}_k^m} \right)} $ | (6) |
4) 反馈R(i,am)
反馈R(i,am)表示在状态i时选择行动am后MPTCP的瞬时吞吐量. 多路并行传输数据时,各个路径的往返时延不同,数据包到达接收端的时间不同,而TCP提供可靠交付的服务,数据包只有按序到达才会被上层获取. 在数据传输时,由于需要等待晚到达的数据包,所以往返时延最大的路径会影响数据传输的吞吐量,将反馈R(i,am)定义为式(7)所示的形式,其中cwkj表示状态j时路径k的窗口值.
| $ R\left( {i,{a_m}} \right) = \sum\limits_{j \in S} {P\left( {j|i,{a_m}} \right)\frac{{\sum\limits_{k \in {R_m}} {cw_k^j} }}{{\mathop {\max }\limits_{k \in {R_m}} {T_k}}}} $ | (7) |
马尔可夫策略由一系列的行动集合构成,使用集合π={π1,π2,…,πl}来表示,其中l表示状态集合S中的状态数量,πi∈A(i). 根据马尔可夫决策过程的平均准则可得到以状态i为起始状态时采用策略π的平均反馈.
| $ V\left( {i,\pi } \right) \equiv \mathop {\lim }\limits_{N \to \infty } \sup \frac{1}{N}\sum\limits_{t = 1}^N {E_i^\pi R\left( {s\left( t \right),{a_\pi }\left( {s\left( t \right)} \right)} \right)} $ | (8) |
其中:s(t)表示在决策时刻t时的系统状态,R(s(t),aπ(s(t)))表示在状态s(t)采取行动aπ(s(t))所获得的立即反馈. 马尔可夫决策过程要解决的问题就是求解出一个最优策略集π*使得反馈V(i,π*)最大.
1.2 应用实例针对现有大多数移动终端提供2个网络接口的实际情况,使用2条路径作为应用实例进行介绍.
2条路径时状态集合S就由2条路径拥塞窗口的组合构成,状态的个数为W12W22.
| $S = \left\{ {\left( {c{w_1},c{w_2}} \right)|c{w_1} \in \left[{1,{W_1}} \right],c{w_2} \in \left[{1,{W_2}} \right]} \right\} $ | (9) |
行动集合Atotal={a1,a2,a3},a1表示同时选择路径1和路径2,a2表示选择路径1,a3表示选择路径2. 由于窗口减半向下取整会出现零值,为了方便表示,定义窗口减半函数如式(10)所示.
| $ h\left( x \right) = \max \left( {\left\lfloor {x/2} \right\rfloor ,1} \right) $ | (10) |
当采取行动a1时,同时使用路径1和路径2进行数据传输,状态的变化有4种[8],状态转移概率如式(11a)~式(11d)所示.
| $ \begin{array}{*{20}{c}} {{P_{{1^ - }{2^ - }}} = P\left( {\left( {h\left( {c{w_1}} \right),h\left( {c{w_2}} \right)} \right)|\left( {c{w_1},c{w_2}} \right),{a_1}} \right) = }\\ {\left( {1 - {{\left( {1 - {p_1}} \right)}^{{\rm{cnt}}_1^1}}} \right)\left( {1 - {{\left( {1 - {p_2}} \right)}^{{\rm{cnt}}_2^1}}} \right)} \end{array} $ | (11a) |
| $ \begin{array}{*{20}{c}} {{P_{{1^ - }{2^ + }}} = P\left( {\left( {h\left( {c{w_1}} \right),c{w_2} + 1} \right)|\left( {c{w_1},c{w_2}} \right),{a_1}} \right) = }\\ {\left( {1 - {{\left( {1 - {p_1}} \right)}^{{\rm{cnt}}_1^1}}} \right){{\left( {1 - {p_2}} \right)}^{{\rm{cnt}}_2^1}}} \end{array} $ | (11b) |
| $ \begin{array}{*{20}{c}} {{P_{{1^ + }{2^ - }}} = P\left( {\left( {c{w_1} + 1,h\left( {c{w_2}} \right)} \right)|\left( {c{w_1},c{w_2}} \right),{a_1}} \right) = }\\ {{{\left( {1 - {p_1}} \right)}^{{\rm{cnt}}_1^1}}\left( {1 - {{\left( {1 - {p_2}} \right)}^{{\rm{cnt}}_2^1}}} \right)} \end{array} $ | (11c) |
| $ \begin{array}{*{20}{c}} {{P_{{1^ + }{2^ + }}} = P\left( {\left( {c{w_1} + 1,c{w_2} + 1} \right)|\left( {c{w_1},c{w_2}} \right),{a_1}} \right) = }\\ {{{\left( {1 - {p_1}} \right)}^{{\rm{cnt}}_1^1}}{{\left( {1 - {p_2}} \right)}^{{\rm{cnt}}_2^1}}} \end{array} $ | (11d) |
其中:${\rm{cnt}}_2^1 = \max \left( {\frac{{c{w_{{\rm{total}}}}}}{{{a_1}}},c{w_1}} \right),{\rm{cnt}}_2^1 = \max \left( {\frac{{c{w_{{\rm{total}}}}}}{{{a_1}}},c{w_2}} \right)$. 当采取行动a2时,只使用路径1进行数据传输,不向路径2调度数据,路径2的拥塞窗口大小不变,状态的变化有2种,状态转移概率如式(12a)~式(12b)所示,式中cnt12=cw1.
| $ \begin{array}{*{20}{c}} {{P_{{1^ - }2}} = P\left( {\left( {h\left( {c{w_1}} \right),c{w_2}} \right)|\left( {c{w_1},c{w_2}} \right),{a_2}} \right) = }\\ {1 - {{\left( {1 - {p_1}} \right)}^{{\rm{cnt}}_1^2}}} \end{array} $ | (12a) |
| $ \begin{array}{*{20}{c}} {{P_{{1^ + }2}} = P\left( {\left( {c{w_1} + 1,c{w_2}} \right)|\left( {c{w_1},c{w_2}} \right),{a_2}} \right) = }\\ {{{\left( {1 - {p_1}} \right)}^{{\rm{cnt}}_1^2}}} \end{array} $ | (12b) |
同理,当采取行动a3时,只使用路径2进行数据传输,不向路径1调度数据,路径1的拥塞窗口大小不变,状态的变化有2种,状态转移概率如式(13a)~式(13b)所示,式中cnt23=cw2.
| $ \begin{array}{*{20}{c}} {{P_{{{12}^ - }}} = P\left( {\left( {c{w_1},h\left( {c{w_2}} \right)} \right)|\left( {c{w_1},c{w_2}} \right),{a_3}} \right) = }\\ {1 - {{\left( {1 - {p_1}} \right)}^{{\rm{cnt}}_2^3}}} \end{array} $ | (13a) |
| $ \begin{array}{*{20}{c}} {{P_{{{12}^ + }}} = P\left( {\left( {c{w_1},c{w_2} + 1} \right)|\left( {c{w_1},c{w_2}} \right),{a_3}} \right) = }\\ {{{\left( {1 - {p_1}} \right)}^{{\rm{cnt}}_2^3}}} \end{array} $ | (13b) |
在状态i时选取不同行动后的预期吞吐量表示反馈. 选取行动a1时使用2条路径进行数据传输,预期吞吐量为2条路径并行传输的吞吐量;选取行动a2和a3时使用1条路径进行数据传输,预期吞吐量即为对应单条路径的吞吐量.
| $ \begin{array}{*{20}{c}} {R\left( {i,{a_1}} \right) = }\\ {{P_{{1^ - }{2^ - }}}\frac{{h\left( {cw_1^i} \right) + h\left( {cw_2^i} \right)}}{{\max \left( {{T_1},{T_2}} \right)}} + {P_{{1^ - }{2^ + }}}\frac{{h\left( {cw_1^i} \right) + cw_2^i + 1}}{{\max \left( {{T_1},{T_2}} \right)}} + }\\ {{P_{{1^ + }{2^ + }}}\frac{{cw_1^i + cw_2^i + 2}}{{\max \left( {{T_1},{T_2}} \right)}} + {P_{{1^ + }{2^ - }}}\frac{{cw_1^i + 1 + h\left( {cw_2^i} \right)}}{{\max \left( {{T_1},{T_2}} \right)}}} \end{array} $ | (14) |
| $ R\left( {i,{a_2}} \right) = {P_{{1^ - }2}}\frac{{h\left( {cw_1^i} \right)}}{{{T_1}}} + {P_{{1^ + }2}}\frac{{cw_1^i + 1}}{{{T_1}}} $ | (15) |
| $ R\left( {i,{a_3}} \right) = {P_{{{12}^ - }}}\frac{{h\left( {cw_2^i} \right)}}{{{T_2}}} + {P_{{{12}^ + }}}\frac{{cw_2^i + 1}}{{{T_2}}} $ | (16) |
使用NS3进行仿真,仿真参数如表1所示. 数据调度使用轮询算法(round robin),拥塞控制使用联合拥塞控制算法(coupled congestion control),接收端数据重组算法使用D_SACK算法. 考虑到实际应用当中的耗时问题,在仿真验证中将策略求解精度和求解时间进行了折中,求解精度设置为10-4,最大迭代次数设置为106.
| 表1 仿真参数 |
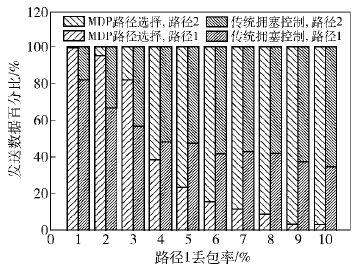
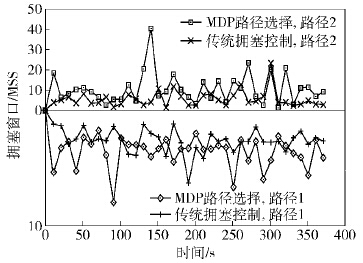
将路径2的丢包率固定为1%,路径1的丢包率从1%增加到10%,测量通过每条路径发送数据的百分比,结果如图1所示. 路径1的丢包率为5%时,测量每条路径的拥塞窗口变化,结果如图2所示.
图1为路径1和路径2在传统的联合拥塞控制和使用路径选择2种情况下发送数据的百分比. 从图1中可以看出,路径选择能更有效地将数据均衡到质量较好的路径上进行传输. 使用联合拥塞控制时,通过路径1传输的数据从81.94%减少到34.66%,通过路径2传输的数据从18.06%增加到65.34%;使用路径选择时,通过路径1传输的数据从99.53%减少到3.02%,通过路径2传输的数据从0.47%增加到96.98%. 这是由于随着路径1丢包率的增加,在联合拥塞控制中路径1窗口减半的概率增加,所以通过路径1的数据比重也会减小,但是由于路径1的往返时延较小,仍然会向路径1分配较多的数据;在使用路径选择时,由于综合考虑了往返时延和丢包率,在路径1的路径质量变差时能够根据路径的真实情况更有效地将数据均衡到路径2上.
图2为路径1丢包率为5%时在传统的联合拥塞控制和使用路径选择2种情况下路径1和路径2拥塞窗口的变化. 从图2中可以看出,当路径1的丢包率为5%时,路径2的质量优于路径1,但联合拥塞控制没有考虑丢包率对吞吐量的影响,不能有效地向路径2均衡数据,并且联合拥塞控制会减小拥塞窗口的增长速率,导致路径2的拥塞窗口增长缓慢. 路径选择会根据拥塞窗口的变化选择不同的路径组合传输数据,将更多的数据均衡到路径质量较好的路径2上,使得路径2的拥塞窗口能够快速增长. 路径选择方法在路径1的拥塞窗口较小时不选择路径1传输数据,避免了路径1的窗口由于丢包而减小,使得路径1的拥塞窗口平均值相对较大.
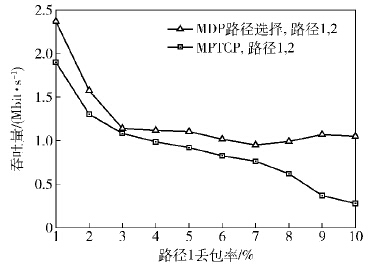
2.2 吞吐量提升结果分析将路径2的丢包率固定为1%,路径1的丢包率从1%增加到10%,观测仿真结果,平均吞吐量变化如图3所示. 平均吞吐量变化表明基于马尔可夫决策过程的路径选择方法可以提高MPTCP的吞吐量,特别是当路径1的丢包率较大时,路径选择能明显地提升吞吐量. 使用路径选择时吞吐量会在减小到一定程度后不再发生大幅度的降低,这是由于路径选择综合考虑了往返时延和丢包率对吞吐量的影响,使用最优化平均吞吐量的路径选择策略,减少了接收端的乱序包和数据包等待,提升了吞吐量.
3 结束语在MPTCP联合拥塞控制的马尔可夫模型的基础上建立了基于马尔可夫决策过程的动态路径选择模型. 动态路径选择方法可以在路径质量变化时有效地将数据均衡到较优路径进行传输,在不影响并行数据传输鲁棒性的基础上提升吞吐量,同时建立的马尔可夫决策模型也可为优化MPTCP其他性能参数提供一定的理论参考.
| [1] | Mao S, Bushmitch D, Narayanan S, et al. MRTP: a multiflow real-time transport protocol for Ad hoc networks[J]. IEEE Transactions on Multimedia, 2006, 8(2): 356-369.[引用本文:1] |
| [2] | Iyengar J R, Amer P D, Stewart R. Concurrent multipath transfer using SCTP multihoming over independent end-to-end paths[J]. IEEE/ACM Transactions on Networking, 2006, 14(5): 951-964.[引用本文:1] |
| [3] | Yabandeh M, Zarifzadeh S, Yazdani N. Improving performance of transport protocols in multipath transferring schemes[J]. Computer Communications, 2007, 30(17): 3270-3284.[引用本文:1] |
| [4] | Ford A, Raiciu C, Handley M, et al. TCP extensions for multipath operation with multiple addresses[J]. Internet Engineering Task Force, RFC, 2013, 6824.[引用本文:1] |
| [5] | Wischik D, Raiciu C, Greenhalgh A, et al. Design, implementation and evaluation of congestion control for multipath TCP[C]//Proceedings of the 8th USENIX Conference on Networked Systems Design and Implementation. Boston: USENIX NSDI, 2011, 11: 8.[引用本文:2] |
| [6] | Ford A, Raiciu C, Handley M, et al. Architectural guidelines for multipath TCP development[J]. Internet Engineering Task Force, RFC, 2011, 6182.[引用本文:1] |
| [7] | Arzani B, Gurney A, Cheng S, et al. Impact of path characteristics and scheduling policies on MPTCP performance[C]//28th International Conference on Advanced Information Networking and Applications Workshops. Victoria, BC: IEEE, 2014: 743-748.[引用本文:1] |
| [8] | 徐明伟, 张志超. MPTCP联合拥塞控制机制的Markov模型[J]. 清华大学学报: 自然科学版, 2012, 52(9): 1281-1285. Xu Mingwei, Zhang Zhichao. Markov modeling of MPTCP's coupled congestion control[J]. Journal of Tsinghua University Science and Technology, 2012, 52(9): 1281-1285.[引用本文:2] |