2. 国网江西省电力公司, 南昌 330077
利用正交频分复用信号包含循环前缀的特点,提出一种针对该信号的多用户场景下的协作检测模型,用最大化偏移系数的方法对系统的权值向量进行优化,得到优化权值向量的闭合表达式. 理论分析和仿真结果均表明,所提算法检测性能优于经典协作检测算法.
2. State Grid Jiangxi Electric Power Company, Nanchang 330077, China
Utilizing the cyclic prefix characteristic of orthogonal frequency division multiplexing(OFDM) signal, this paper optimizes the system weight vector with the improved maximum deflection coefficient, proposes a multiuser cooperation detection algorithm, and obtains optimized weight vector expression. Theoretical analysis and simulation results demonstrate the remarkable improvement of proposed algorithm on detection performance compared with the classical cooperation detection algorithm.
如何对授权频谱进行有效感知是认知无线技术中的重点和难点,多用户协作频谱检测利用空间上的分集,有效地提高了检测效率[1]. 但大多数协作感知技术在较低信噪比(SNR,signal noise ratio)时检测效率低下[2]. 认知无线电中认知用户(CR,cognitive relay)对正交频分复用(OFDM,orthogonal frequency division multiplexing)信号的检测已经成为近年来研究的热点. Chaudhari等[3]采样单个符号块信号,比对循环前缀(CP,cyclic prefix)位置判断是否存在OFDM信号,Bokharaiee等[4]把这种检测范围扩大到多个符号块. Axell等[5]在Chaudhari等[3]的基础上进行了改进,利用同步技术,只采样OFDM符号块中CP段的数据,提出最优NP检测算法(ONPD,optimal NEYMAN-PEARSON detector). 但未利用到空间分集技术提升检测性能.
将ONPD算法运用到对OFDM信号的协作检测中,提出一种新的协作检测算法,采用偏移系数最大化对认知加权向量进行优化,并求出优化后权值的闭合表达式. 所提出的检测算法性能优于基于能量检测的协作检测算法,利用偏移系数最大化的合并算法也优于其他软合并算法.
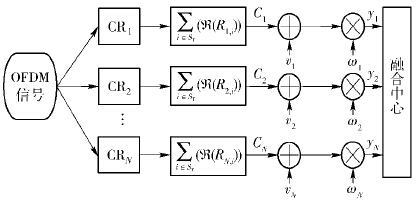
1 系统检测模型 1.1 单点检测模型模型假设主用户(PU,primary user)发送OFDM制式信号,每个OFDM符号中长度包含Nd的数据序列和长度为Nc的循环前缀,在每个感知周期Ts内,共采样到K+1个OFDM符号块,其中包含有K个完整的OFDM符号数.
模型中CR对PU信号的检测采用最优NP检测算法,该算法复杂度较低,适用于多用户分集检测. CR接收到的信号x中包含有K个连续的OFDM符号,定义接收信号采样的值积为${r_i} \buildrel \Delta \over = {x_i}x_{i + {N_{\rm{d}}}}^*,{R_i} \buildrel \Delta \over = \frac{1}{K}\sum\limits_{k = 0}^{K - 1} {{r_{i + k\left( {{N_{\rm{c}}} + {N_{\rm{d}}}} \right)}},i = 0,\cdots ,{N_{\rm{c}}} + {N_{\rm{d}}} - 1} $. 当PU发送OFDM信号时,Ri为感知周期内单个CP与重复部分的值积的累积,当PU不工作时,Ri为高斯噪声值积的累积. Sτ为CP所在位置的集合,R(·)为复数的实数部分的值. 检测算法的判决公式为
| $ C = \sum\limits_{i \in {S_\tau }} {\left( {R\left( {{R_i}} \right)} \right)\frac{{\mathop > \limits^{{{\rm{H}}_{\rm{1}}}} }}{{\mathop < \limits_{{{\rm{H}}_0}} }}} \lambda $ | (1) |
整个系统采用线性加权方式,如图1所示,设有N个CR用户对PU信号同时进行检测. 感知过程分为感知阶段和报告阶段,感知阶段接收信号为
| $ {x_i}\left( t \right) = \left\{ \begin{array}{l} {n_i}\left( t \right)\;\;\;{H_0}\;\;\;0 \le t \le {T_s}\\ {h_i}s\left( t \right) + {n_i}\left( t \right)\;\;\;{H_1}\;\;\;i = 1,2,\cdots ,N \end{array} \right. $ | (2) |
其中:xi(t)为接收复OFDM信号,hi为PU到CRi的衰减因子,s(t)为OFDM发射信号,s(t)~Nc(0,σs2),ni(t)为该信道的噪声分量,ni(t)~Nc(0,σn,i2),Nc(·)为复高斯分布. CR采用ONPD算法对发射信号xi(t)进行检测,在报告阶段把检测结果通过完全正交的报告信道发送到融合中心(FC,fusion center),融合中心接收到的信号为yi(t)=Ci+vi,用线性加权的方法融合接收的数据,与设定门限值比较,判断是否存在PU.
2 性能分析 2.1 单点性能分析 Axell等[5]给出了Rn,i分布,由于Rn,i(i)i∈Sτ相互独立,推导第i个CR的检测结果Ci=$\sum\limits_{i \in {S_\tau }} {\left( {R\left( {{R_i}} \right)} \right)} $分布为
| $ {D_i} \sim \left\{ \begin{array}{l} N\left( {0,\frac{{{N_{\rm{c}}}\sigma _{n.i}^4}}{{2K}}} \right)\;\;\;{{\rm{H}}_0}\\ N\left( {{N_{\rm{c}}}h_i^2\sigma _{\rm{s}}^2,{N_{\rm{c}}}\frac{{h_i^4\sigma _{\rm{s}}^4 + \sigma _{n.i}^4/2 + h_i^2\sigma _{\rm{s}}^2 + \sigma _{n.i}^2}}{K}} \right)\;\;\;{{\rm{H}}_1} \end{array} \right. $ | (3) |
在H0和H1两种检测条件下,Ci的期望和方差分别为
| $ \left. \begin{array}{l} {\mu _{0,i}} = E\left( {{C_i}|{H_0}} \right) = 0\\ {\mu _{1,i}} = E\left( {{C_i}|{H_1}} \right) = {N_{\rm{c}}}h_i^2\sigma _{\rm{s}}^2 \end{array} \right\} $ | (4) |
| $ \left. \begin{array}{l} {\xi _{0,i}} = {\mathop{\rm var}} \left( {{C_i}|{{\rm{H}}_0}} \right) = \frac{{{N_{\rm{c}}}\sigma _{n.i}^4}}{{2K}}\\ {\xi _{1,i}} = {\mathop{\rm var}} \left( {{C_i}|{H_1}} \right) = {N_{\rm{c}}}\frac{{h_i^4\sigma _{\rm{s}}^4 + \sigma _{n.i}^4/2 + h_i^2\sigma _{\rm{s}}^2 + \sigma _{n.i}^2}}{K} \end{array} \right\} $ | (5) |
融合中心通过报告信道接收各CR检测到的数据{Ci},根据图1和式(3),CR接收数据{yi}服从高斯分布,期望为E(yi)=E(Ci),方差为
| $ \left. \begin{array}{l} {\xi _{0,i}} = {\mathop{\rm var}} \left( {{y_i}|{H_0}} \right) = \frac{{{N_{\rm{c}}}\sigma _{n.i}^4}}{{2K}} + \sigma _{v,i}^2\\ {\xi _{1,i}} = {\mathop{\rm var}} \left( {{y_i}|{H_1}} \right) = {N_{\rm{c}}}\frac{{h_i^4\sigma _{\rm{s}}^4 + \sigma _{n.i}^4/2 + h_i^2\sigma _{\rm{s}}^2 + \sigma _{n.i}^2}}{K} + \sigma _{v,i}^2 \end{array} \right\} $ | (6) |
融合中心接收{yi}之后,采用线性融合算法处理采集到的数据,最终判决是否存在OFDM信号.
| $ {y_c} = \sum\limits_{i = 1}^N {{\omega _i}{y_i} = {\omega ^{\rm{T}}}y} \frac{{\mathop > \limits^{{{\rm{H}}_{\rm{1}}}} }}{{\mathop < \limits_{{{\rm{H}}_0}} }}\gamma $ | (7) |
其中:γ为全局判决门限值,权值向量为ω$ \buildrel \Delta \over = $[ω1,ω2,…,ωN]T,反映对融合结果贡献的大小,ω的值相关于感知信道与报告信道的状态.
3 性能优化算法偏移系数是反映二元检测算法性能的单一参数,采用最大化偏移系数的方法对权值建模优化,偏移系数的求解公式分为2类:分母分别采用var(yc|H0)和var(yc|H1),采用改进的偏移系数优化方法,优化目标为选择合适的ω,使得d2(ω)最大化,建模为
| $ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\arg \max \;\;{d^2}\left( \omega \right) = }\\ {\frac{{{{\left( {E\left( {{y_{\rm{c}}}|{{\rm{H}}_{\rm{1}}}} \right) - E\left( {{y_{\rm{c}}}|{{\rm{H}}_{\rm{0}}}} \right)} \right)}^2}}}{{p{\mathop{\rm var}} \left( {{y_{\rm{c}}}|{{\rm{H}}_{\rm{1}}}} \right) + \left( {1 - p} \right){\mathop{\rm var}} \left( {{y_{\rm{c}}}|{{\rm{H}}_{\rm{1}}}} \right)}} = }\\ {\frac{{{{\left( {{\omega ^{\rm{T}}}{\mu _1}} \right)}^2}}}{{p\left( {{\omega ^{\rm{T}}}\sum {_1\omega } } \right) + \left( {1 - p} \right)\left( {{\omega ^{\rm{T}}}\sum {_0\omega } } \right)}}} \end{array}}\\ {0 \le p \le 1} \end{array} $ | (8) |
由于ω是唯一变量,‖ω‖=1;d2(ω)为ω的连续函数,故d2(ω)存在最大值,最大值所在点为满足$\frac{{\partial {d^2}\left( \omega \right)}}{{\partial \omega }} = 0$时向量ω的值. 推出
| $ \begin{array}{*{20}{c}} {\frac{{\partial {d^2}\left( \omega \right)}}{{\partial \omega }} = \frac{{2{\mu _1}\mu _1^{\rm{T}}\left( {p\sum {_1} + \left( {1 - p} \right)\sum {_0} } \right)\omega }}{{{{\left( {{\omega ^{\rm{T}}}\left( {p\sum {_1} + \left( {1 - p} \right)\sum {_0} } \right)\omega } \right)}^2}}} - }\\ {\frac{{2{{\left( {{\omega ^{\rm{T}}}{\mu _1}} \right)}^2}\left( {p\sum {_1} + \left( {1 - p} \right)\sum {_0} } \right)\omega }}{{{{\left( {{\omega ^{\rm{T}}}\left( {p\sum {_1} + \left( {1 - p} \right)\sum {_0} } \right)\omega } \right)}^2}}} = 0} \end{array} $ | (9) |
根据式(9)得出优化的权值为
| $ \begin{array}{*{20}{c}} {{\omega _{{\rm{opt}}}} = \frac{{{\omega ^{\rm{T}}}\left( {p\sum {_1} + \left( {1 - p} \right)\sum {_0} } \right)\omega }}{{{\omega ^{\rm{T}}}{\mu _1}}} \times }\\ {{{\left( {p\sum {_1} + \left( {1 - p} \right)\sum {_0} } \right)}^{ - 1}}{\mu _1}} \end{array} $ | (10) |
由于${\frac{{{\omega ^{\rm{T}}}\left( {p\sum {_1} + \left( {1 - p} \right)\sum {_0} } \right)\omega }}{{{\omega ^{\rm{T}}}{\mu _1}}}}$为大于0的实数,对权值向量的比例关系不构成影响,所以ωopt是归一化的权值向量,为
| $ {\omega _{{\rm{opt}}}} = \varepsilon {\left( {p\sum {_1} + \left( {1 - p} \right)\sum {_0} } \right)^{ - 1}}{\mu _1} $ | (11) |
其中$\varepsilon = \frac{1}{{\left\| {{{\left( {p\sum {_1} + \left( {1 - p} \right)\sum {_0} } \right)}^{ - 1}}{\mu _1}} \right\|}}$.
4 仿真验证对所提算法的性能进行仿真验证. 系统采用蒙特卡罗仿真,感知信道为高斯衰落信道,平均信噪比为常数值,假设报告阶段FC无衰减地接收来自CRi的信号,仿真模型如图2所示.
图2为CP数和OFDM块的数量不同时仿真性能的比较. 仿真中CR用户数为N=5,报告信道的平均信噪比为-10 dB,ONPD算法中CP数的大小直接决定字符串的长度,CP的长度也决定了检测的性能.由图2可以看出,OFDM模块的CP越长,采样的OFDM符号块越多,系统检测性能越优.
式(11)改进偏移系数公式中的不同p值决定了优化权值ω存在差异,仿真图3是p值不同时系统检测性能的比较,仿真条件为-2 dB,感知时间内采样的符号块N=5. 循环前缀个数Nc=5. 由图3可知,算法检测性能随着p的增大非线性增加.
图4所示为OFDM优化后协作算法、最大比合并(MRC,maximal ratio combing)算法和协作能量检测之间的算法比较,报告信道的平均信噪比为-2 dB,能量检测采用MRC合并算法. 需要说明的是,由于平均信噪比很小,使得在p=0和p=1时权值向量ω的差别微乎其微,使得检测性能曲线在p=0和p=1几乎重合. 图4仿真结果表明,所提优化算法性能优于MRC协作检测和能量检测,用户数N越大,检测性能越好. 相比于经典能量协助检测算法,本模型在单点CR上采用复杂度更高、性能更好的ONPD检测算法. 考虑报告信道噪声条件,用最大化偏移系数的方法求出最优的权值,复杂度大于MRC协助检测算法中的权值求解算法,性能也更优.
5 结束语对ONPD算法性能进行了分析,推导了该算法的性能参数. 提出了针对OFDM信号的多用户协作检测模型,求出了系统性能参数,并用最大化偏移系数的方法对加权系数进行优化,求出了权值表达式. 仿真结果表明,所提出的算法有明显的性能优势.
| [1] | 王秋才, 袁超伟, 张金波, 等. SC-FDMA上行系统中一种频域迭代块DFE均衡方法[J]. 西安电子科技大学学报, 2013, 40(2): 25-30. Wang Qiucai, Yuan Chaowei, Zhang Jinbo, et al. Frequency domain iterative block DFE for SC-FDMA uplink system[J]. Journal of Xidian University, 2013, 40(2): 25-30.[引用本文:1] |
| [2] | 李映雪, 沈树群, 袁超伟, 等. 认知无线电中改进的低复杂度联合检测方法[J]. 北京邮电大学学报, 2013, 36(2): 89-92. Li Yingxue, Shen Shuqun, Yuan Chaowei, et al. A joint spectral detection algorithm with low complexity in cognitive radio[J]. Journal of Beijing University of Posts and Telecommunications, 2013, 36(2): 89-92.[引用本文:1] |
| [3] | Chaudhari S, Koivunen V, PoorH V. Autocorrelation-based decentralized sequential detection of OFDM signals in cognitive radios[J]. Signal Processing, IEEE Transactions on, 2009, 57(7): 2690-2700.[引用本文:2] |
| [4] | Bokharaiee S, Nguyen H H, Shwedyk E. Blind spectrum sensing for OFDM-based cognitive radio systems[J]. IEEE Transactions on Vehicular Technology, 2011, 60(3): 858-871.[引用本文:1] |
| [5] | Axell E, Larsson E G. Optimal and sub-optimal spectrum sensing of OFDM signals in known and unknown noise variance[J]. IEEE Journal on Selected Areas in Communications, 2011, 29(2): 290-304.[引用本文:2] |