提出了一种基于最小定位误差限的Wi-Fi指纹定位接入点位置优化方法.利用费歇尔信息矩阵的特性,分析了定位误差与不同信号强度分布的数学关系.首先,根据信号强度分布特性的不同,将定位目标区域划分为若干子区域;然后,推导出定位目标区域所对应的平均定位误差限;最后,利用模拟退火算法搜索最优接入点位置使得平均定位误差限达到最小. 仿真结果表明,此方法可以有效提高Wi-Fi位置指纹定位法的精度.
A new access point placement optimization approach based on lowest positioning error bound in Wi-Fi fingerprint based localization was proposed. Analysis towards the theoretical relationship between positioning error and various signal distributions by using Fisher information matrix was presented. The target environment was divided into several subareas based on signal distributions. And then, the average error bound corresponding to the target environment was derived out. Thirdly, the heuristic simulated annealing algorithm towards the lowest average error bound to optimize access point locations was adopted. Simulation demonstrates that the proposed access point placement optimization approach effectively improves the precision of Wi-Fi fingerprint based localization.
随着用户对信息即时性和就地性需求越来越强烈,基于位置的服务也备受关注.在Wi-Fi定位[1]系统中,位置指纹定位方法的精度较高且无需添加额外基础硬件设施,从而得到了较为广泛的应用.
Wi-Fi接入点(AP,access point)位置对定位误差存在较大影响.现有方法中,为了优化AP位置,主要关注因素有信号覆盖范围、通信服务质量、信号传输速率等[2, 3]. 然而,现有方法不能很好地描述AP位置与指纹定位方法精度的数学依赖关系.因此利用费歇尔信息矩阵[4]分析定位误差与不同信号强度分布的数学关系,并且推导了指纹定位方法的定位误差限. 此外,根据AP位置与定位误差限的依赖关系,利用模拟退火算法对AP位置进行优化,进而提高指纹定位方法的精度.
1 系统描述最小定位误差限的Wi-Fi定位AP位置优化的系统结构包括3个部分,即定位目标区域划分、定位误差限计算以及AP位置优化. 在定位区域内,信噪比不同,信号强度的统计特性也不相同.当接收信号中存在较多直射信号时,信噪比较大,令信号接收强度(RSS,received signal strength)服从高斯分布;当信号中存在较多散射信号时,信噪比较小,令RSS服从瑞利分布;当信号中存在直射信号和散射信号时,令RSS服从莱斯分布. 由于接收来自不同AP的RSS不可能服从某单一分布,因此根据用户与各AP位置的距离将区域进行划分,求出实际环境中混合信号分布的误差限. 根据区域划分情况,计算实际定位误差限,从而得到对应的定位误差限. 将定位误差限作为模拟退火目标函数,得到最小定位误差限下的最优AP位置.
2 AP位置优化假设Wi-Fi信号传播特性服从多墙模型,于是接收端接收到的信号强度P的计算表达式为
| $ P = P\left( {{d_0}} \right) - 10\beta \lg \left( {d/{d_0}} \right) - {P_{\rm{w}}} - \chi $ | (1) |
其中:d0为参考距离,β为路径损耗指数,d为传播距离,Pw为墙面的损耗,χ为随机变量.
设第i个用户为θi=(xi,yi)T,xi和yi表示第i个用户的横纵坐标,估计位置为θ′i=(x′i,y′i)T,则θ′i的均方误差矩阵var[θ′i]为
| $ {\mathop{\rm var}} \left[{{\theta _i}'} \right] = {E_0}\left\{ {\left( {{\theta _i}' - {\theta _i}} \right){{\left( {{\theta _i}' - {\theta _i}} \right)}^{\rm{T}}}} \right\} = \left[{\begin{array}{*{20}{c}} {\delta _{{x_i}'}^2}&{{\delta _{{x_i}'{y_i}'}}}\\ {{\delta _{{y_i}'{x_i}'}}}&{\delta _{{y_i}'}^2} \end{array}} \right] $ | (2) |
其中:δx′i2和δy′i2为平均平方误差,δx′iy′i和δy′ix′i为x′i和y′i协方差.根据克拉美罗界不等式,有
| $ {\mathop{\rm var}} \left[{{\theta _i}'} \right] \ge {\left\{ {J\left( {{\theta _i}'} \right)} \right\}^{ - 1}} $ | (3) |
其中J(θi)为θi的费歇尔信息矩阵. fθi(P)为在θi处接收到的信号强度P的概率分布函数,从而定义Score函数U(θ)为fθi(P)的对数函数梯度,即
| $ U\left( {{\theta _i}} \right) = \nabla \ln {f_\theta }\left( P \right) = \frac{\partial }{{\partial \theta }}\ln {f_{{\theta _i}}}\left( P \right) $ | (4) |
由于J(θi)=var[U(θi)],根据式(5)得到E[U(θi)]=0,于是$J\left( {{\theta _i}} \right) = E{\left[{\frac{\partial }{{\partial \theta }}\ln {f_{{\theta _i}}}\left( P \right)} \right]^2}$.
| $ \begin{array}{*{20}{c}} {E\left[{U\left( {{\theta _i}} \right)} \right] = E\left[{\frac{\partial }{{\partial \theta }}\ln {f_{{\theta _i}}}\left( P \right)} \right] = }\\ {\int {\frac{\partial }{{\partial \theta }}\ln \left( {{f_{{\theta _i}}}\left( P \right)} \right)\left( {1/{f_{{\theta _i}}}\left( P \right)} \right){f_{{\theta _i}}}\left( P \right){\rm{d}}P = 0} } \end{array} $ | (5) |
用户从AP处接收到的RSS服从高斯分布,m个相互独立AP的RSS联合概率密度函数为
| $ {f_{{\theta _i}}}\left( P \right) = \prod\limits_{k = 1}^m {1/\sqrt {2\pi } {\sigma _1}\exp \left( { - {\xi ^2}/2\sigma _1^2} \right)} $ | (6) |
其中:ξ=P-P(d0)+10βlg(dik)+Pw,dik=$\sqrt {{{\left( {{x_i} - {x_k}} \right)}^2} + {{\left( {{y_i} - {y_k}} \right)}^2}} $(xk和yk为第k个AP的横纵坐标,如图1所示);σ1为高斯分布的标准差;根据图1,式(6)可简化为
| $ {f_{{\theta _i}}}\left( P \right) = \prod\limits_{k = 1}^m {1/\sqrt {2\pi } {\sigma _1}\exp \left\{ { - {\rho _1}/2{{\left( {\ln {d_{ik}}} \right)}^2}} \right\}} $ | (7) |
其中ρ1=(10β/σ1ln10)2.
另外,有
| $ J\left( {{\theta _i}} \right) = \left[{\begin{array}{*{20}{c}} {{J_{xx}}\left( {{\theta _i}} \right)}&{{J_{xy}}\left( {{\theta _i}} \right)}\\ {{J_{yx}}\left( {{\theta _i}} \right)}&{{J_{yy}}\left( {{\theta _i}} \right)} \end{array}} \right] $ | (8) |
由式(5)可得ln dik期望值为零,于是有
| $ \left. \begin{array}{l} {J_{xx}}\left( {{\theta _i}} \right) = {\rho _1}\sum\limits_{k = 1}^m {{{\left[{\cos {\alpha _{ik}}/{d_{ik}}} \right]}^2}} \\ {J_{xy}}\left( {{\theta _i}} \right) = {J_{yx}}\left( {{\theta _i}} \right) = {\rho _1}\sum\limits_{k = 1}^m {\sin {\alpha _{ik}}\cos {\alpha _{ik}}/{d_{ik}}^2} \\ {J_{yy}}\left( {{\theta _i}} \right) = {\rho _1}\sum\limits_{k = 1}^m {{{\left[{\sin {\alpha _{ik}}/{d_{ik}}} \right]}^2}} \end{array} \right\} $ | (9) |
其中αik为第i个用户与第k个AP的连线与x轴的夹角,如图1所示.由于
| $ {\left\{ {J\left( {{\theta _i}} \right)} \right\}^{ - 1}} = \frac{1}{{\left| {J\left( {{\theta _i}} \right)} \right|}}\left[{\begin{array}{*{20}{c}} {{J_{yy}}\left( {{\theta _i}} \right)}&{ - {J_{yx}}\left( {{\theta _i}} \right)}\\ { - {J_{xy}}\left( {{\theta _i}} \right)}&{{J_{xx}}\left( {{\theta _i}} \right)} \end{array}} \right] $ | (10) |
其中|J(θi)|=Jxx(θi)Jyy(θi)-Jxy2(θi),可得
| $ \left. \begin{array}{l} \delta _{{x_i}'}^2 = E{\left( {{x_i}' = {x_i}} \right)^2} \ge J_{xx}^{ - 1}\\ \delta _{{y_i}'}^2 = E{\left( {{y_i}' = {y_i}} \right)^2} \ge J_{yy}^{ - 1} \end{array} \right\} $ | (11) |
关于第i个用户的定位误差限V1(θi)为
| $ \begin{array}{*{20}{c}} {{V_1}\left( {{\theta _i}} \right) = J_{xx}^{ - 1} + J_{yy}^{ - 1} = \frac{{{J_{xx}} + {J_{yy}}}}{{{J_{xx}}{J_{yy}} - J_{xy}^2}}}\\ {\frac{{\frac{1}{{{\rho _1}}}\left( {\sum\limits_{k = 1}^m {{{\left[{\frac{{\cos {\alpha _{ik}}}}{{{d_{ik}}}}} \right]}^2} + \sum\limits_{k = 1}^m {{{\left[{\frac{{\sin {\alpha _{ik}}}}{{{d_{ik}}}}} \right]}^2}} } } \right)}}{{\sum\limits_{k = 1}^m {{{\left[{\frac{{\sin {\alpha _{ik}}}}{{{d_{ik}}}}} \right]}^2}} \sum\limits_{k = 1}^m {{{\left[{\frac{{\cos {\alpha _{ik}}}}{{{d_{ik}}}}} \right]}^2} - \left[{\sum\limits_{k = 1}^m {{{\left[{\frac{{\sin {\alpha _{ik}}\cos {\alpha _{ik}}}}{{d_{ik}^2}}} \right]}^2}} } \right]} }}} \end{array} $ | (12) |
用户从AP接收到的RSS服从瑞利分布,RSS的联合概率密度函数可以表示为
| $ {f_{{\theta _i}}}\left( P \right) = \prod\limits_{k = 1}^m {\left( {\xi /{\sigma _2}^2\exp \left[{ - {\xi ^2}/2\sigma _2^2} \right]} \right)} $ | (13) |
其中${\sigma _2} = \sqrt {2{\mathop{\rm var}} \left( \xi \right)/4 - \pi } $.
同理,可以得到
| $ \left. \begin{array}{l} {J_{xx}}\left( {{\theta _i}} \right) = \sum\limits_{k = 1}^m {s{{\left[{\cos {\alpha _{ik}}/{d_{ik}}} \right]}^2}} \\ {J_{xy}}\left( {{\theta _i}} \right) = {J_{yx}}\left( {{\theta _i}} \right) = \sum\limits_{k = 1}^m {s\sin {\alpha _{ik}}\cos {\alpha _{ik}}/{d_{ik}}^2} \\ {J_{yy}}\left( {{\theta _i}} \right) = \sum\limits_{k = 1}^m {s{{\left[{\sin {\alpha _{ik}}/{d_{ik}}} \right]}^2}} \end{array} \right\} $ | (14) |
其中s=(10β/σ2ln10)2+1/ln2dik. 从而,得到第i个用户的定位误差限V2(θi).
2.3 莱斯分布用户接收到的RSS服从莱斯分布,RSS的联合概率密度函数可以表示为
| $ {f_{{\theta _i}}}\left( P \right) = \prod\limits_{k = 1}^m {\left( {\xi /{\sigma _3}^2\exp \left( { - \frac{{{\xi ^2} + {A^2}}}{{2{\sigma _3}^2}}} \right){{\rm{I}}_0}\left( {\frac{{A\xi }}{{{\sigma _3}^2}}} \right)} \right)} $ | (15) |
其中:σ32为噪声功率,A为信号幅度,I0(·)为修正的0阶贝塞尔函数.
同理,可以得到
| $ \left. \begin{array}{l} {J_{xx}}\left( {{\theta _i}} \right) = \sum\limits_{k = 1}^m {f{{\left[{\cos {\alpha _{ik}}/{d_{ik}}} \right]}^2}} \\ {J_{xy}}\left( {{\theta _i}} \right) = {J_{yx}}\left( {{\theta _i}} \right) = \sum\limits_{k = 1}^m {f\sin {\alpha _{ik}}\cos {\alpha _{ik}}/{d_{ik}}^2} \\ {J_{yy}}\left( {{\theta _i}} \right) = \sum\limits_{k = 1}^m {f{{\left[{\sin {\alpha _{ik}}/{d_{ik}}} \right]}^2}} \end{array} \right\} $ | (16) |
其中
| $ \begin{array}{*{20}{c}} {f = {{\left( {\frac{{10\beta }}{{{\sigma _3}\ln 10}}} \right)}^2} + \frac{1}{{{{\ln }^2}{d_{ik}}}} + }\\ {\frac{{10\beta A}}{{\ln 10}}\frac{{\frac{{A\xi }}{{{\sigma _3}^2}}I_0^2\left( {\frac{{A\xi }}{{\sigma _3^2}}} \right) + I_1^2\left( {\frac{{A\xi }}{{\sigma _3^2}}} \right) - {I_0}\left( {\frac{{A\xi }}{{\sigma _3^2}}} \right){I_1}\left( {\frac{{A\xi }}{{\sigma _3^2}}} \right)}}{{\frac{{A\xi }}{{\sigma _3^2}}I_0^2\left( {\frac{{A\xi }}{{\sigma _3^2}}} \right)}}} \end{array} $ |
从而得到第i个用户的定位误差限V3(θi).
2.4 平均定位误差限在实际中,来自不同AP的RSS可能服从不同信号分布.从一般性考虑,令来自m1个相互独立AP的RSS服从高斯分布,m2个相互独立AP的RSS服从瑞利分布,m3个相互独立AP的RSS服从莱斯分布.基于此,接收到的来自m个相互独立AP的RSS联合概率密度函数为
| $ {f_{{\theta _i}}}\left( P \right) = {f_{{\theta _i}}}\left( {{P_1}} \right){f_{{\theta _i}}}\left( {{P_2}} \right) = {f_{{\theta _i}}}\left( {{P_3}} \right) $ | (17) |
其中fθi(P1)、fθi(P2)和fθi(P3)如式(6)、式(13)和式(15)所示.
根据上述结果,可以得到
| $ \left. {\begin{array}{*{20}{c}} {J{'_{xx}}\left( {{\theta _i}} \right) = }\\ {\sum\limits_{{k_1} = 1}^{{m_1}} {{\rho _1}{{\left[ {\frac{{\cos {\alpha _{i{k_1}}}}}{{{d_{i{k_1}}}}}} \right]}^2} + \sum\limits_{{k_2} = 1}^{{m_2}} {s{{\left[ {\frac{{\cos {\alpha _{i{k_2}}}}}{{{d_{i{k_2}}}}}} \right]}^2} + } \sum\limits_{{k_3} = 1}^{{m_3}} {f{{\left[ {\frac{{\cos {\alpha _{i{k_3}}}}}{{{d_{i{k_3}}}}}} \right]}^2}} } }\\ {J{'_{xy}}\left( {{\theta _i}} \right) = J{'_{yx}}\left( {{\theta _i}} \right) = }\\ {\sum\limits_{{k_1} = 1}^{{m_1}} {{\rho _1}\frac{{\sin {\alpha _{i{k_1}}}\cos {\alpha _{i{k_1}}}}}{{{d_{i{k_1}}}^2}} + \sum\limits_{{k_2} = 1}^{{m_2}} {s\frac{{\sin {\alpha _{i{k_2}}}\cos {\alpha _{i{k_2}}}}}{{{d_{i{k_2}}}^2}} + } } }\\ {\sum\limits_{{k_3} = 1}^{{m_3}} {f\frac{{\sin {\alpha _{i{k_3}}}\cos {\alpha _{i{k_3}}}}}{{{d_{i{k_3}}}^2}}} }\\ {J{'_{yy}}\left( {{\theta _i}} \right) = }\\ {\sum\limits_{{k_1} = 1}^{{m_1}} {{\rho _1}{{\left[ {\frac{{\sin {\alpha _{i{k_1}}}}}{{{d_{i{k_1}}}}}} \right]}^2} + \sum\limits_{{k_2} = 1}^{{m_2}} {s{{\left[ {\frac{{\sin {\alpha _{i{k_2}}}}}{{{d_{i{k_2}}}}}} \right]}^2}} + \sum\limits_{{k_3} = 1}^{{m_3}} {f{{\left[ {\frac{{\sin {\alpha _{i{k_3}}}}}{{{d_{i{k_3}}}}}} \right]}^2}} } } \end{array}} \right\} $ | (18) |
从而,当RSS统计特性服从此混合分布时,得到第i个用户的平均定位误差限V(θi).
因此,整个定位目标区域所对应的平均定位误差限V为
| $ V = 1/n\sum\limits_{i = 1}^n {V\left( {{\theta _i}} \right)} $ | (19) |
其中n为定位目标区域内用户可能位置的总数.
3 仿真结果实验仿真环境如图2所示,在12 m×12 m的方形区域内均匀标记144个用户可能位置,相邻位置间距为0.8 m.
3.1 AP数目的变化基于上述结果,当AP数目从k增加到k+1时,定位误差限的变化情况为
| $ {\frac{{{{\left( {\begin{array}{*{20}{c}} {\frac{{\sin {\alpha _{i\left( {m + 1} \right)}}}}{{{d_{i\left( {m + 1} \right)}}}}\sqrt {{\eta _{im}}{{\sum\limits_{k = 1}^m {\left[{\frac{{c\cos {\alpha _{ik}}}}{{{d_{ik}}}}} \right]} }^2} - {\omega _{im}}} }\\ {\frac{{ - \frac{{\cos {\alpha _{i\left( {m + 1} \right)}}}}{{{d_{i\left( {m + 1} \right)}}}}\sqrt {{\eta _{im}}{{\sum\limits_{k = 1}^m {\left[{\frac{{c\sin {\alpha _{ik}}}}{{{d_{ik}}}}} \right]} }^2} - {\omega _{im}}} }}{{}}} \end{array}} \right)}^2}}}{{\left( {{\omega _{im}}{\omega _{i\left( {m + 1} \right)}}} \right)}}} $ | (20) |
其中
| $ \begin{array}{*{20}{c}} {{\eta _{im}} = {{\sum\limits_{k = 1}^m {\left[{\frac{{c\cos {\alpha _{ik}}}}{{{d_{ik}}}}} \right]} }^2} + {{\sum\limits_{k = 1}^m {\left[{\frac{{c\sin {\alpha _{ik}}}}{{{d_{ik}}}}} \right]} }^2}}\\ {{\omega _{im}} = {{\sum\limits_{k = 1}^m {\left[{\frac{{c\sin {\alpha _{ik}}}}{{{d_{ik}}}}} \right]} }^2}{{\sum\limits_{k = 1}^m {\left[{\frac{{c\cos {\alpha _{ik}}}}{{{d_{ik}}}}} \right]} }^2} - }\\ {{{\left[{\sum\limits_{k = 1}^m {\frac{{{c^2}\sin {\alpha _{ik}}\cos {\alpha _{ik}}}}{{{d_{ik}}^2}}} } \right]}^2}} \end{array} $ |
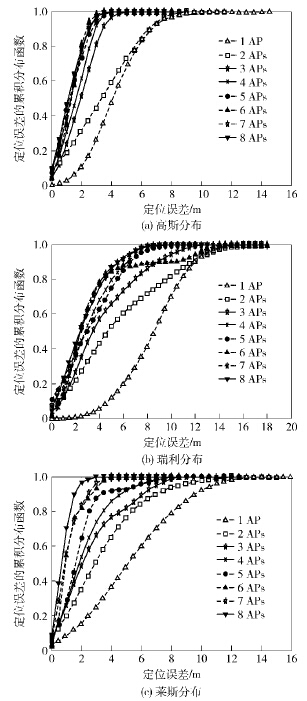
当RSS服从高斯分布、瑞利分布和莱斯分布时,有c=ρ1,c=s,c=f. 由于ωimωi(m+1)>0,可得AP数目的增加将减小定位误差限,且当αi(m+1)=αik,k∈{1,2,…,m}(所有AP共线)时,有Vm(θi)=Vm+1(θi).图3给出了当RSS统计特性服从高斯分布、瑞利分布和莱斯分布时,定位误差随AP数目的变化情况.由图3可以看到,随着AP数目的增加,定位精度在整体上是提高的,然而当AP数目大于3时,定位精度的变化不明显.
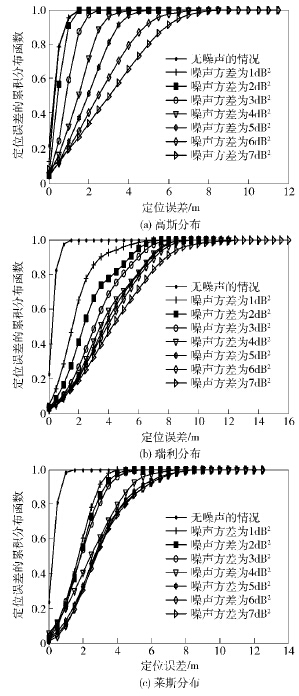
3.2 噪声功率的变化图4给出了当RSS服从高斯分布、瑞利分布和莱斯分布时,定位误差随噪声功率变化情况.可以看到,随着噪声功率增大,定位精度恶化.此外,当RSS服从高斯分布时,噪声功率变化对定位误差影响较大,在大信噪比下,噪声功率变化会显著影响定位精度.
4 结束语提出了最小定位误差限的Wi-Fi定位AP位置优化方法. 利用费歇尔信息矩阵,推导在不同RSS统计特性条件下用户可能位置处的定位误差限,得到目标区域所对应的定位误差限.将定位误差限作为模拟退火算法目标函数搜索最优AP位置.通过仿真实验,对不同AP数目和信号强度分布下的最优AP位置和定位误差进行分析.
| [1] | Zhou Mu, Wong Albert, Tian Zengshan, et al. Personal mobility map construction for crowd-sourced Wi-Fi based indoor mapping [J]. IEEE Communications Letters, 2014, 18(8): 1427-1430.[引用本文:1] |
| [2] | Fang Shih-Hau, Lin Tsung. A novel access point placement approach for WLAN-based location systems [C]//Abbas Jamalipour. 2010 IEEE WCNC. Sydney: IEEE, 2010: 1-4.[引用本文:1] |
| [3] | Zhao Yongxiang, Zhou Huaibei, Li Meifang. Indoor access points location optimization using differential evolution [C]//Anthony Skjellum. Computer Science and Software Engineering. Hubei:IEEE, 2008: 382-385.[引用本文:1] |
| [4] | Shen Yuan, Wymeersch Henk, Win Moe. Fundamental limits of wideband cooperative localization via Fisher information [C]//General Chairs. 2007 IEEE WCNC. Kowloon:IEEE, 2007: 3951-3955.[引用本文:1] |