2. 北京邮电大学 信息安全中心, 北京 100876;
3. 国网河南省电力公司 南阳供电公司, 河南 南阳 473008
针对大秘密共享存在效率和安全方面的不足,提出一个可验证多次使用动态门限大秘密共享方案. 为了提高效率,将大秘密分解,且表示为较小有限域上的矩阵,并利用了二元单向函数. 为了增强安全性,推广门限动态调整方法,利用了椭圆曲线群上离散对数. 理论分析结果表明,该方案不仅存储等效率大大提高,还能抵抗不诚信参与者攻击,且重建过程中秘密份额始终保密无须更新. 尤其当参与者信任发生变化或参与者人数变动时,门限值能够被t个可信参与者及时调整.
2. Information Security Center, Beijing University of Posts and Telecommunications, Beijing 100876, China;
3. Nanyang Power Supply Company, State Grid Henan Electric Power Company, Henan Nanyang 473008, China
For the efficiency and security problems of large secret sharing, a verifiable multi-use dynamic thres hold large secret sharing scheme was put forward. To improve the efficiency, the large secret is divided and represented as a matrix over smaller finite field, and the two-variable one-way function is also utilized; to enhance security, the thres hold modification method is slightly expanded and the elliptic curve discrete logarithm problem is employed. By analysis, this new scheme not only is high-efficiency, but also can prevent dishonest participants from cheating. Meanwhile, the secret shadows can always be kept secret and need not to be renewed in the process of reconstruction. Especially, when the mutual trust varies or the number of the participants belonging to an organization fluctuates, the threshold value will be adjusted by at least t credible participants in time.
秘密共享技术在密钥管理和安全多方计算等方向有着广泛的应用,因而秘密共享技术一直是信息安全领域的一个重要研究方向.
Shamir[1]和Blakley[2]分别独立提出秘密共享概念和门限秘密共享方案. 可是研究发现Shamir(t,n)门限方案存在2点缺陷:1)当秘密被参与者恢复后,分配者需通过安全信道重新分配一个新的秘密份额给每个参与者;2)即使t个参与者中有一个参与者提供虚假秘密份额,其他参与者只能恢复出错误的秘密,只有提供虚假份额的参与者可以获得正确的秘密. 为了克服上述缺陷,多次使用秘密共享方案被设计出[3, 4],具有验证功能的秘密共享方案被广泛关注[5, 6, 7, 8],且大量动态门限秘密共享方案不断涌现出来[9, 10, 11].
此外,为了满足特殊需求,Zhao等[12]设计出大秘密共享方案,但是该方案研究的重点仅为如何降低存储花费. 于是笔者以将大秘密分解并表示为较小有限域上的矩阵为核心提出一个新的大秘密共享方案,该方案不仅提高效率,还降低存储代价,同时克服初始秘密共享方案的所有缺陷.
1 预备知识 1.1 二元单向函数函数f(r,x)表示任意一个二元单向函数,映射任意变量r和x到固定长度的比特串. 二元单向函数具有如下性质:
1) 给定r和x,容易计算f(r,x);
2) 给定x和f(r,x),计算r是困难的;
3) 不知道x任何信息,对于任意r,计算f(r,x)是困难的;
4) 给定x,寻找2个互不相同的值r1和r2,使得f(r1,x)=f(r2,x)是困难的;
5) 给定r和f(r,x),计算x是困难的;
6) 给定一对ri和f(ri,x),对于r′≠ri,计算f(r′,x)是困难的.
1.2 门限动态调整方法由于实际应用中参与者信任值或参与者人数随时可能发生变化,如何设计动态门限方案变成一个亟待解决的问题. 重点介绍一种高效改变门限参数的方法[11].
1) 一个由至少t个被选举出的参与者组成的集合Δ. 每个参与者Pi∈Δ,随机选取一个t′阶多项式gi(x)且使gi(0)=f(i),他们分别发送gi(j)给参与者Pj(1≤j≤n),其中gi(j)被称为辅助份额,借助它可以重新分享初始秘密份额.
2) 计算公开参量为
| $ r_i^\Delta = \prod\limits_{j \in \Delta ,j \ne i} {\frac{j}{{j - i}},i \in \Delta } $ | (1) |
3) 每一个参与者Pj(1≤j≤n)按照要求擦掉初始秘密份额,然后利用来自其他参与者的辅助份额计算他自己的新份额为
| $ {\phi _j} = \sum\limits_{i = \Delta } {\left( {r_i^\Delta {g_i}\left( j \right)} \right)} $ | (2) |
4) 假设包含至少t′个被选举出的参与者集合Δ′,所有参与者Pj∈Δ′一起利用拉格朗日插值公式恢复秘密为
| $ \alpha = \sum\limits_{i = \Delta '} {\left( {r_i^{\Delta '}{\phi _j}} \right)} $ | (3) |
为了更好地实现笔者的方案,需要将常用的有限域上多项式函数和拉格朗日插值公式进一步推广到向量空间上. 首先令Fq是一个包含q个元素的有限域,其中q是素数的阶,n是一个正整数. 通常用
| $ F_q^{\left( n \right)} = \left\{ {{{\left( {{x_1},{x_2},\cdots ,{x_n}} \right)}^{\rm{T}}}\left| {{x_i} \in {F_q},i = 1,2,\cdots ,n} \right.} \right\} $ | (4) |
表示一个n维列向量空间. 向量空间Fq(n)上多项式函数为
| $ \begin{array}{*{20}{c}} {f\left( x \right) = \left( {\begin{array}{*{20}{c}} {{a_{01}}}\\ {{a_{02}}}\\ \vdots \\ {{a_{0n}}} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {{a_{11}}}\\ {{a_{12}}}\\ \vdots \\ {{a_{1n}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{x_1}}\\ {{x_2}}\\ \vdots \\ {{x_n}} \end{array}} \right) + \cdots \left( {\begin{array}{*{20}{c}} {{a_{\left( {n - 1} \right)1}}}\\ {{a_{\left( {n - 1} \right)2}}}\\ \vdots \\ {{a_{\left( {n - 1} \right)n}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {x_1^{n - 1}}\\ {x_2^{n - 1}}\\ \vdots \\ {x_n^{n - 1}} \end{array}} \right) = }\\ {\left( {\begin{array}{*{20}{c}} {{a_{01}}}\\ {{a_{02}}}\\ \vdots \\ {{a_{0n}}} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {{a_{11}}{x_1}}\\ {{a_{12}}{x_2}}\\ \vdots \\ {{a_{1n}}{x_n}} \end{array}} \right) + \cdots + \left( {\begin{array}{*{20}{c}} {{a_{\left( {n - 1} \right)1}}x_1^{n - 1}}\\ {{a_{\left( {n - 1} \right)2}}x_2^{n - 1}}\\ \vdots \\ {{a_{\left( {n - 1} \right)n}}x_n^{n - 1}} \end{array}} \right)} \end{array} $ | (5) |
向量空间Fq(n)上拉格朗日插值公式为
| $ \begin{array}{*{20}{c}} {f\left( x \right) = \sum\limits_{i = 1}^t {f\left( {\left( {\begin{array}{*{20}{c}} {{k_{i1}}}\\ {{k_{i2}}}\\ \vdots \\ {{k_{in}}} \end{array}} \right)} \right)} \prod\limits_{j = 1.j \ne i}^t {\frac{{\left( {\begin{array}{*{20}{c}} {{x_1}}\\ {{x_2}}\\ \vdots \\ {{x_n}} \end{array}} \right) - \left( {\begin{array}{*{20}{c}} {{k_{j1}}}\\ {{k_{j2}}}\\ \vdots \\ {{k_{jn}}} \end{array}} \right)}}{{\left( {\begin{array}{*{20}{c}} {{k_{i1}}}\\ {{k_{i2}}}\\ \vdots \\ {{k_{in}}} \end{array}} \right) - \left( {\begin{array}{*{20}{c}} {{k_{j1}}}\\ {{k_{j2}}}\\ \vdots \\ {{k_{jn}}} \end{array}} \right)}} = } }\\ {\left( {\begin{array}{*{20}{c}} {\sum\limits_{i = 1}^t {f\left( {{k_{i1}}} \right)\prod\limits_{j = 1.j \ne i}^t {\frac{{x - {k_{j1}}}}{{{k_{i1}} - {k_{j1}}}}} } }\\ {\sum\limits_{i = 1}^t {f\left( {{k_{i2}}} \right)\prod\limits_{j = 1.j \ne i}^t {\frac{{x - {k_{j2}}}}{{{k_{i2}} - {k_{j2}}}}} } }\\ \vdots \\ {\sum\limits_{i = 1}^t {f\left( {{k_{in}}} \right)\prod\limits_{j = 1.j \ne i}^t {\frac{{x - {k_{jn}}}}{{{k_{in}} - {k_{jn}}}}} } } \end{array}} \right)} \end{array} $ | (6) |
根据实际安全性和存储要求,级联一个字符串β(|β| < |S|)到秘密S后面使得整个字符串S′是t和t′乘积的整数倍,然后S′被分割且表示成一个t′×t矩阵P,其中t是方案门限值,由参与者人数和安全级别决定,|β|和t′是2个随机变量. 它们之间存在一个重要的关系表达式为
| $ d = \frac{{\left| S \right| + \left| \beta \right|}}{{tt'}} = \frac{1}{t}\left( {\frac{{\left| S \right|}}{{t'}} + \frac{{\left| \beta \right|}}{{t'}}} \right) $ | (7) |
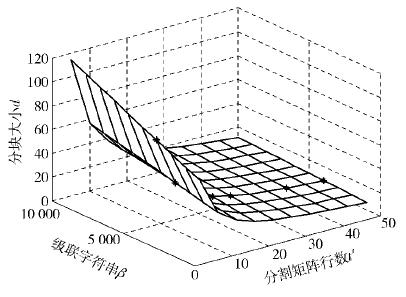
其中d是分割后每个数据块的尺寸. 当存储空间确定时,寻找较小|β|和较大t′,使得d符合要求,如图1所示.
图1表示当门限值t=35,S大小为1 kbit时,随机变量|β|和t′变化时,d大小变化规律图,其中黑色*表示d可能的取值,根据实际需求确定出合适的d.
2 (t,n)门限大秘密共享方案 2.1 分发阶段1) 分发者(简记为D)随机选取一个大秘密S,利用上述思想根据实际安全和存储需求,在大秘密S后面级联一个比特串β,使得整个比特串S′是t和t′乘积的整数倍. 特别注意|β|尽可能小,t′尽可能大,使d达到实际需求. 然后分发者将整个字符串S′分割成tt′个子秘密si∈Fq(q=2d),满足关系式S′=s1||s2||…||stt′,其中“||”表示级联. 最后分发者将所有子秘密按顺序排列得到矩阵为
| $ P = \left( {\begin{array}{*{20}{c}} {{s_1}}&{{s_2}}& \cdots &{{s_t}}\\ {{s_{t + 1}}}&{{s_{t + 2}}}& \cdots &{{s_{2t}}}\\ \vdots & \vdots &{}& \vdots \\ {{s_{t\left( {t' - 1} \right) + 1}}}&{{s_{t\left( {t' - 1} \right) + 2}}}& \cdots &{{s_{tt'}}} \end{array}} \right) $ | (8) |
2) 分发者D将P分解成t份pi(i=0,…,n-1)满足关系P=(p0,p1,…,pt-1),每一份是一个t′维列向量.
3) 如1.3小节所述,分发者D利用上述t个向量pi构造一个向量空间上t-1阶多项式h(x)=p0+p2x+…+pt-1xt-1mod q,并选取n个互不相同t′维列向量ki,计算yi=h(ki),1≤i≤n.
4)分发者D 发送秘密份额(ki,yi)给每一个参与者Ui,1≤i≤n.
2.2 重构阶段不失一般性,假设存在t个参与者Ui (i=1,…,t)想要恢复大秘密S.
1) 每一个参与者Ui贡献他自己的秘密份额(ki,yi),(i=1,…,t).
2) 根据t个参与者贡献的秘密份额(ki,yi)(i=1,…,t),利用1.3小节推广的拉格朗日插值公式,t-1阶多项式函数h(x)能够被重建,即p0,p1,…,pt-1被得到,因为它们是矩阵P的列向量,所以参与者获得大秘密S.
2.3 效率分析效率方面主要统计大秘密恢复过程所需的乘法操作和求逆操作,容易发现该方案中每个参与者仅需较低存储空间且拥有较高效率.
1) 假设n个参与者想要分享一个大秘密S. 在整个协议的执行过程中,该方案中每个参与者至多需要存储尺寸为$\frac{{2\left( {\left| S \right| + \left| \beta \right|} \right)}}{t}$的秘密份额,其中|β|根据实际需要选取且满足条件(|β|<|S|). 而Shamir方案中,参与者需要存储尺寸为2|S|的秘密份额. 显然该方案中每个参与者仅需较少的存储空间.
2) 考虑整个秘密重构过程中计算花费,对于分享同样的大秘密,该方案效率明显高于Shamir秘密共享方案. 不失一般性,假设t个参与者想要恢复大秘密S,对于Shamir方案而言,需要在有限域Fqn1上执行2t(t-1)次乘法操作和t次求逆操作,其中n1>$\frac{{tt'}}{2}$,因为|β| < |S|. 而该方案需要执行$\frac{{{t^2}\left( {t - 1} \right)t' + 2t\left( {t - 1} \right)t'}}{2}$次乘法操作和tt′次求逆操作. 然而,通常在有限域上执行1次乘法操作和1次求逆操作需要花费为O(d2)和O(d3)(最新算法能将求逆操作时间复杂性降到O(d2)). 假设n1取最小值$\frac{{tt'}}{2}$,2种算法的效率分析如表1所示.
| 表1 秘密恢复计算花费 |
其中†Fq表示有限域Fq上的求逆操作.
综上所述,显然笔者方案中每个参与者仅需较低存储空间且拥有较高效率.
3 可验证多次使用动态门限大秘密共享方案假设分发者只存在初始化阶段和分发阶段,此后t个被选出的参与者会根据实际安全需求一起调整方案的门限值.
3.1 初始化阶段第1步 令D和U1,U2,…,Un分别表示分发者和n个参与者. 首先分发者D随机选择1个大素数q1≥3和2个正整数a和b,使得Eq1(a,b)为有限域Fq1上一条椭圆曲线,并且Eq1(a,b)包含一个素数p阶椭圆曲线群H= < g>,满足在该椭圆曲线群上求解离散对数问题是困难的. 此外,分发者D随机选取一个二元单向函数f(r,x),最后公布公共信息q 1,p,g和f(r,x).
第2步 每一个参与者Ui随机选取一个元素xi∈Fq1作为自己的初始秘密份额并通过安全信道发送xi给分发者D,D必须保证xi≠xj,一旦xi=xj,D要求参与者Ui重新选取秘密份额xi,直到所有的秘密份额xi(1≤i≤n)互不相同.
3.2 分发阶段前2步和第2节所述方案一样,不作详细介绍.
3) 如1.3小节所述,分发者D利用上述t个向量pi构造一个向量空间上t-1阶多项式h(x)=p0+p2x+…+pt-1xt-1mod q. 对每个t′维列向量ki=(f(r1,xi),f(r2,xi),…,f(rt′,xi))Tmod p,计算yi=h(ki),1≤i≤n.
4) 分发者D计算y′i=gyi mod q1(1≤i≤n),并通过安全信道发送yi给参与者Ui,1≤i≤n.
5) 分发者D公布公共参数(r1,r2,…,rt′;k1,k2,…,kn;y′1,y′2,…,y′n;f(r,x)).
3.3 门限修改阶段1) 假设包含t个被选出的参与者集合Δ,每个参与者Ui∈Δ随机选取一个t″阶多项式hi(x)满足hi(0)=yi并计算yli=hi(kl)和y′li=gylimod q1,然后公布y′li和发送yli给参与者Ul(1≤l≤n). 利用辅助秘密份额yli重新分享旧秘密份额.
2) 计算公共参数为
| $ r_i^\Delta = \prod\limits_{j \in \Delta ,j \ne i} {\frac{{x - {k_j}}}{{{k_i} - {k_j}}},i \in \Delta } $ | (9) |
3)每个参与者按照要求擦去旧的秘密份额,利用辅助份额计算新的秘密份额为
| $ {\phi _l} = \sum\limits_{i = \Delta } {\left( {r_i^\Delta {h_i}\left( {{k_l}} \right)} \right)} $ | (10) |
不失一般性,假设存在t个参与者想要恢复大秘密S.
1) 每个参与者贡献他自己所拥有的辅助份额yli,任何参与者都能通过验证等式验证其真伪. 如果验证等式
2) 根据公开信息并利用拉格朗日插值公式多项式能够被重建,能够得到P的列向量p0,p1,…,pt-1,即得到秘密S. 方法为
| $ \begin{array}{*{20}{c}} {h\left( x \right) = \sum\limits_{l \in \Delta '} {{\phi _l}} \prod\limits_{m \in \Delta ',m \ne l} {\frac{{ - {k_m}}}{{{k_m} - {k_l}}}} = }\\ {\sum\limits_{l \in \Delta '} {\sum\limits_{i \in \Delta } {\prod\limits_{j \in \Delta ,j \ne i} {\prod\limits_{m \in \Delta ',m \ne l} {\frac{{x - {k_j}}}{{{k_i} - {k_j}}}\frac{{ - {k_m}}}{{{k_m} - {k_l}}}{h_i}\left( {{k_l}} \right)} } } } } \end{array} $ | (11) |
本文方案和几种经典方案的功能比较如表2所示.
| 表2 本文方案和几种经典方案的功能比较 |
值得注意的是,Shamir(t,n)门限秘密共享方案中一个提供虚假秘密份额的不诚信参与者Ui不会被发现,除了不诚信参与者Ui外,其他参与者只能恢复出一个错误秘密. 而在笔者的方案中,修改过门限值后,不诚信参与者不被发现,只有他提供的辅助份额能够通过验证等式y′li=gylimod q1. 可是如果不诚信参与者成功,说明他能够成功解决椭圆曲线上离散对数难题.
此外,就合谋攻击而言,当t″>t时,对于内部不诚信参与者,该协议安全性和初始协议安全性一样,因为内部不诚信参与者,可能没有按要求擦掉旧的秘密份额;当t″<t时,协议安全性基于新的门限值t″. 对于外部攻击者,协议的安全性始终依赖方案的门限值. 进一步,由于二元单向函数的性质和初始秘密份额是由每个参与者自己选取的,所以每个参与者的秘密份额xi始终是保密的. 因此,笔者的方案不仅可以抵抗外部攻击还可以抵抗内部攻击.
4 结束语首先提出一种新思想,将任意大秘密分解并表示成一个较小有限域上的矩阵,该思想有助于大秘密共享方案降低存储代价和提高方案效率. 然后,根据上述思想,利用已存在的二元单向函数、椭圆曲线上离散对数难题和笔者推广的动态门限改变方法,设计出一个新的可验证多次使用动态门限大秘密共享方案. 该方案不仅克服了Shamir等门限方案只能使用一次且不能抵抗来自不诚信参与者攻击的不足,还能有效地解决实际应用中参与者信任变化和参与者人员变动问题.
| [1] | Shamir A. How to share a secret[C]//Communications of the ACM, 1979, 22(11): 612-613.[引用本文:2] |
| [2] | Blakley G R. Safeguarding cryptographic keys[J]. In Proc NCC, AFIPS Press, 1979, 48: 313-317.[引用本文:2] |
| [3] | He J, Dawson E. Multistage secret sharing based on one-way function[J]. Electronics Letters, 1994, 30(19): 1591-1592.[引用本文:2] |
| [4] | Lin H Y, Yeh Y S. Dynamic multi-secret sharing scheme[J]. Int J Contemp Math Sciences, 2008(3): 37-42.[引用本文:2] |
| [5] | Chor B, Goldwasser S, Micali S, et al. Verifiable secret sharing and achieving simultaneity in the presence of faults[C]//In 26th Annual Symposium on Foundations of Computer Science, IEEE, 1985: 383-395.[引用本文:2] |
| [6] | Eslami Z, Zarepour A J. A verifiable multi-secret sharing scheme based on cellular automata[J]. Information Sciences, 2010, 180: 2889-2894.[引用本文:2] |
| [7] | Hu C Q, Liao X F, Cheng X Z. Verifiable multi-secret sharing based on LESR sequences[J]. Theoretical Computer Science, 2012, 445: 52-62.[引用本文:2] |
| [8] | Shao J. Efficient verifiable multi-secret sharing scheme based on hash function[J]. Information Sciences, 2014, 278: 104-109.[引用本文:2] |
| [9] | Martin K M, Pieprzyk J, Safavi-Naini R, et al. Changing thresholds in the absence of secure channels[C]//In 4th Australasian Conference Information Security and Privacy, ACISP, 1999, 1587: 177-191.[引用本文:2] |
| [10] | Tartary C, Wang H X. Dynamic threshold and cheater resistance for shamir secret sharing scheme[C]//In 2nd SKLOIS Conference on Information Security and Cryptology, 2006, 318: 103-117.[引用本文:2] |
| [11] | Nojoumian M, Stinson D R. On dealer-free dyna mic threshold schemes[J]. Advance in Mathema Tics of Communications, 2013(7): 39-56.[引用本文:3] |
| [12] | Zhao D W, Peng H P, Wang C, et al. Secret sharing scheme with short share realizing (t,n) threshold and adversary structure[J]. Computers and Mathematics with Applications, 2012, 64(4): 611-615.[引用本文:2] |