无线传感器网络由大量能够感知环境参数的传感器节点组成，这些节点通过无线通信方式形成自组织网络,可广泛应用于环境监测与保护、医疗护理、目标跟踪及军事侦测等领域. 由于传感器节点所处环境往往较为复杂以及成本限制等原因,单个传感器的观测信息并不能直接反映感知对象的真实物理状态，据其可能做出错误判决. 为了降低节点误判对系统整体性能的影响，可以利用决策融合技术对多个传感器的判决信息进行融合，以获得对同一事件更完全、更准确的描述^[1]. 与传统的分布式决策融合不同，无线传感器网络中的决策融合要考虑节点能量受限、系统资源受限以及信道衰落的影响. 为了降低传输能耗，Rago等^[2]针对低传输速率环境，提出了仅当传感器判决有事件发生时才向融合中心发送信息的筛选传输策略. 在此基础上，Cheng等^[3]提出了三级量化的传输策略，并与传统的传输策略进行了比较. Wang等^[4] 进一步对传感器个数未知条件下的决策融合问题进行了研究，并给出了最优筛选概率的选取方法. 考虑到无线信道对局部决策传输的影响,一些学者结合信道信息对带宽受限并行无线传感器网络决策融合问题进行了研究^{[5, 6]}. 上述文献的研究工作均是基于瑞利衰落信道模型进行的. 瑞利衰落信道模型适用于传感器与融合中心之间只有散射，不存在视距传播的情形. 如果存在视距传播，则可以建模为莱斯衰落信道. 笔者在莱斯衰落信道模型下，对使用三级量化筛选策略的传感器网络决策融合问题进行了研究，并给出了理论分析和仿真结果.

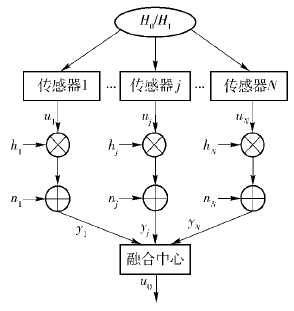
分布式传感器网络决策融合系统由传感器节点、无线信道及融合中心3部分组成，如图1所示. 系统中有N个传感器节点，所观测的事件称为H，H₁表示有事件发生，H₀表示没有事件发生.

Figure 1

		Figure Option View Download New Window
		图1 分布式传感器网络决策融合系统模型

在三级量化筛选策略下，传感器观测值经量化后输出局部判决为

其中：θ_0j、θ_1j为量化区间的端点，Z_j为传感器观测值. 此时，传感器的检测概率和虚警概率分别为p_dj=P(u_j=1|H₁)和p_fj=P(u_j=1|H₀). 定义传感器筛选概率为p_cj=P(H₁)q_1j+P(H₀)q_0j，其中q_1j=P(u_j=0|H₁)，q_0j=P(u_j=0|H₀)，P(H₀)、P(H₁)分别为H₀、H₁发生的先验概率.

局部判决u_j经无线信道后输出为

其中：h_j为信道增益，这里服从莱斯分布；n_j为信道噪声，且服从均值为0、方差为σ²的高斯分布. 将传输信号的平均能量标准化，则h_j的概率密度函数为

其中：I₀(·)为第一类零阶修正贝塞尔函数，K为莱斯因子.

融合中心接收到y₁,…,y_j,…,y_N后，根据融合规则做出全局决策u₀. 融合系统的检测错误概率为

在三级量化筛选策略下，通过改变筛选概率值，可以得到不同的检测错误概率. 当检测错误概率最小时，筛选概率值达到最优. 根据检测错误概率随筛选概率变化的关系曲线，可以比较不同融合算法的性能，并获得最优的筛选概率值.

假设各个传感器的观测相互独立，且信道实时状态信息(CSI,channel state information)和节点性能参数已知，则融合中心的似然比融合规则Λ_CSI为

进一步在低信噪比和高信噪比条件下对融合规则Λ_CSI进行近似处理,可以得到2种简化的融合规则.

1) 当SNR→0时，融合规则Λ_CSI可以近似为融合规则Λ₁，即

如果各个节点的性能参数相同，Λ₁可进一步简化为融合规则Λ_MRC(maximum ratio combiner)，即

其中τ_MRC为判决门限.

融合规则Λ_MRC无须节点性能参数，与融合规则Λ_CSI相比，需要预知的信息更少，计算量也更小.

2) 当SNR→∞时，融合规则Λ_CSI可以近似为融合规则Λ_CV(Chair-Varshney)，即

融合规则Λ_CV仅需节点性能参数，因而对系统要求更低. 但在低信噪比时，由于算法的近似处理，检测性能会有所降低.

似然比融合规则Λ_CSI在理论上是最优的^[7]，但它需要知道CSI，实现起来较为困难. 融合规则Λ_MRC和Λ_CV虽然算法简单,容易实现,但检测性能与最优算法还有一定的差距. 为此，下面寻求替代CSI进行似然比决策融合的方法，即推导基于莱斯信道统计分布信息的次优决策融合规则.

当信道增益服从单位功率的莱斯分布时，Wang等^[8]给出条件概率密度为

其中：t=1+2(1+K)σ²，Γ(·)为伽玛函数，D_n(·)为抛物圆柱面函数.

由式(9)可以计算条件概率密度P(y_j|H₀)和P(y_j|H₁)，进一步可以得到基于信道统计分布信息的决策融合规则Λ_CS(channel statistics)，即

其中 $\xi \left( i \right) = \frac{{{{\left( {K + {K^2}} \right)}^i}}}{{{{\left( {i!} \right)}^2}}}{\left( {\frac{t}{{{\sigma ^2}}}} \right)^{ - \left( {i + 1} \right)}}\Gamma \left( {2i + 2} \right). $

当SNR→0时,Λ_CS可进一步近似为融合规则Λ₂，即

其中Q_0j和Q_1j分别定义为

证明 当SNR→0时，σ→∞，仅保留 $\sum\limits_{i = 0}^\infty {\xi \left( i \right){D_{ - \left( {2i + 2} \right)}}\left( {\frac{{ - {y_j}}}{{\sigma \sqrt t }}} \right)} $中的前2项，有

由 $\mathop {\lim }\limits_{x \to 0} {D_{ - n}}\left( x \right) = a + bx,a = \frac{{\sqrt x }}{{{2^{n/2}}\Gamma \left( {\frac{{n + 1}}{2}} \right)}},b = - \frac{{\sqrt {2\pi } }}{{{2^{n/2}}\Gamma \left( n \right)}} $可得

同理，有

将式(15)和式(16)代入式(10)，应用近似公式 $\mathop {\lim }\limits_{x \to 0} \lg \left( {1 + x} \right) = x$，可得

当节点性质相同时，Q_0j和Q_1j也是常数，即Q_0j=Q₀，Q_1j=Q₁，略去常数项，Λ₂可进一步简化为Λ_EGC(equal gain combiner)，即

其中τ_EGC为判决门限.

可见，融合规则Λ_EGC需要预知的信息最少，算法最简单. 但是，在高信噪比时，由于算法的近似处理，检测性能会有所下降.

当各个传感器观测独立且检测性能相同时，融合规则Λ_MRC和Λ_EGC的统计量将是一系列独立同分布的随机变量之和. 如果N较大，根据中心极限定理，Λ_MRC和Λ_EGC的统计量近似服从正态分布. 表1给出了H₀和H₁条件下Λ_MRC和Λ_EGC统计量的均值和方差. 利用高斯近似，可得Λ_MRC和Λ_EGC的检测错误概率为

表1

表1

表1 H0和H1条件下ΛMRC和ΛEGC统计量的均值和方差 H ΛMRC ΛEGC H0 $ \begin{array}{l} {\mu _{{0_{MRC}}}} = 2{p_f} + {q_0} - 1\\ \sigma _{{0_{MRC}}}^2 = \frac{1}{N}\left[ {\frac{{2\left( {1 - {q_0}} \right)}}{{{{\left( {K + 1} \right)}^2}}}1{F_1}\left( { - 2,1; - K} \right) + {\sigma ^2} - {{\left( {2{p_f} + {q_0} - 1} \right)}^2}} \right] \end{array} $ $ \begin{array}{l} {\mu _{{0_{EGC}}}} = \sqrt {\frac{\pi }{{4\left( {K + 1} \right)}}} 1{F_1}\left( { - \frac{1}{2},1; - K} \right)\left( {2{p_f} + {q_0} - 1} \right)\\ \sigma _{{0_{EGC}}}^2 = \frac{1}{N}\left[ {1 - {q_0} + {\sigma ^2} - \frac{\pi }{{4\left( {K + 1} \right)}}} \right.1{F_1}^2\\ \;\;\;\;\;\;\;\;\;\;\left( { - \frac{1}{2},1; - K} \right)\left. {{{\left( {2{p_f} + {q_0} - 1} \right)}^2}} \right] \end{array} $ H1 $ \begin{array}{l} {\mu _{{1_{MRC}}}} = 2{p_d} + {q_1} - 1\\ \sigma _{{1_{MRC}}}^2 = \frac{1}{N}\left[ {\frac{{2\left( {1 - {q_1}} \right)}}{{{{\left( {K + 1} \right)}^2}}}1{F_1}\left( { - 2,1; - K} \right) + {\sigma ^2} - {{\left( {2{p_d} + {q_1} - 1} \right)}^2}} \right] \end{array} $ $ \begin{array}{l} {\mu _{{1_{EGC}}}} = \sqrt {\frac{\pi }{{4\left( {K + 1} \right)}}} 1{F_1}\left( { - \frac{1}{2},1; - K} \right)\left( {2{p_f} + {q_1} - 1} \right)\\ \sigma _{{1_{EGC}}}^2 = \frac{1}{N}\left[ {1 - {q_1} + {\sigma ^2} - \frac{\pi }{{4\left( {K + 1} \right)}}} \right.1{F_1}^2 \end{array} $

表1 H0和H1条件下ΛMRC和ΛEGC统计量的均值和方差

其中

本节使用Matlab7.11对各个融合规则进行仿真，Monte Carlo仿真次数为10⁶次. 假设H₀和H₁等概率发生，节点观测值服从高斯分布，有H₀∶Z_j～N(0,1)，H₁∶Z_j～N(m,1)，且各个节点性质相同，传感器个数N=20.

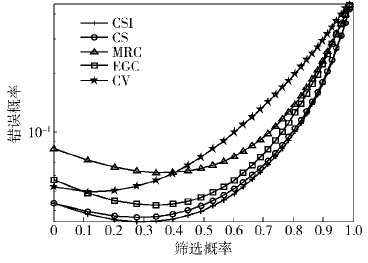
图2为通过Monte Carlo仿真得到的检测错误概率随筛选概率变化的曲线，此时莱斯因子K=2，信道信噪比为10dB，观测信号强度m=1. 图2中，当筛选概率值为0时，对应于无筛选的传统传输策略. 随着筛选概率值的增加，检测错误概率先减小后增加. 曲线最低点对应的筛选概率为最优筛选概率，此时系统检测错误概率达到最小. 这表明，三级量化筛选策略的引入可以改善系统的检测性能. 同时，当传感器判决为0时，不用传输判决信息，从而有效降低了系统传输能耗. 表2是在不同信噪比情况下，当传感器筛选概率设定为p_c=0.1时，5种融合规则的检测错误概率的比较结果. 由图2和表2的仿真结果看，Λ_CSI的检测错误概率最小，性能最好；Λ_CS性能其次，但与Λ_CSI非常接近. 进一步比较3种简化的融合规则，在高信噪比时，Λ_CV检测性能较好；在低信噪比时，Λ_MRC检测性能却较好；而Λ_EGC在整个信噪比范围内均有较好的性能，鲁棒性不错.

Figure 2

		Figure Option View Download New Window
		图2 不同融合规则的错误概率曲线

表2

表2

表2 不同融合规则的检测错误概率比较 SNR/dB 融合规则 ΛCSI ΛCS ΛCV ΛMRC ΛEGC -10 0.3052 0.3056 0.3498 0.3058 0.3156 -5 0.2032 0.2058 0.2559 0.2085 0.2139 0 0.1092 0.1136 0.1482 0.1271 0.1196 5 0.0577 0.0585 0.0762 0.0875 0.0686 10 0.0383 0.0394 0.0496 0.0725 0.0493 20 0.0312 0.0315 0.0413 0.0666 0.0416

表2 不同融合规则的检测错误概率比较

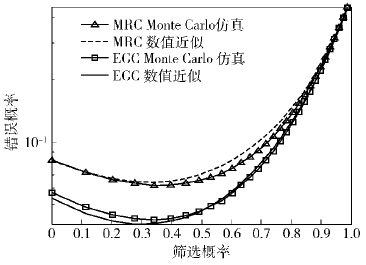
图3为分别通过Monte Carlo仿真和数值近似得到的融合规则Λ_MRC和Λ_EGC的检测错误概率曲线. 由图3可以看出,在筛选概率较小时，Λ_MRC的Monte Carlo仿真曲线与数值近似曲线吻合程度较为理想；

Figure 3

		Figure Option View Download New Window
		图3 ΛMRC、ΛEGC的错误概率曲线

而在筛选概率较大时，Λ_EGC的Monte Carlo仿真曲线与数值近似曲线吻合程度良好.

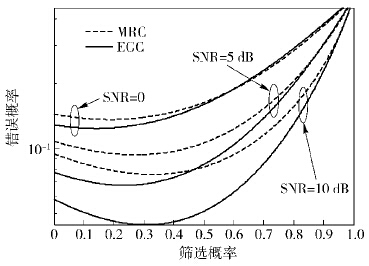
图4为检测错误概率与信噪比的关系曲线，此时K=1，m=1. 由图4可知，随着信噪比增大，最优筛选概率也相应增加. 这是由于信噪比越大，信道越可靠，此时传感器的错误判决经过信道传输后会直接造成系统检测性能的下降，因而有必要通过增加筛选概率来降低传输错误判决的可能性.

Figure 4

		Figure Option View Download New Window
		图4 检测错误概率与信噪比的关系

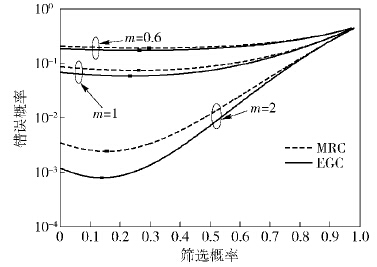
图5为检测错误概率与观测信号强度m的关系曲线，此时K=3，SNR为5dB. 由图5可知，随着m的增加，最优筛选概率值却相应减小. 这是由于m值越大，观测信号越可靠，传感器误判的可能性就越低，此时筛选概率也应该相应降低，以便尽可能多地传输节点判决信息.

Figure 5

		Figure Option View Download New Window
		图5 检测错误概率与m的关系

笔者研究了三级量化筛选策略下的传感器网络决策融合问题，给出了基于CSI的最优融合规则以及基于莱斯信道统计分布信息的次优融合规则，并对上述融合规则进行了简化. 通过理论分析和仿真实验比较了这几种融合规则在检测性能、计算复杂度和耗费系统资源方面的优劣，并探讨了最优筛选概率与信道信噪比、观测信号强度的关系.