针对无线传感网络中节点被俘获导致融合值偏离的问题,提出了一种基于信任的态势数据融合机制,根据历史信任与节点数据相关度,制定信任度感知规则,并分3个阶段确保数据完整性. 首先,事件检测时,运用最可信多数规则,提升事件检测的准确性;其次,数据融合时,运用数据筛选规则处理不可靠数据,提升数据可靠性;最后,一致性检测时,采用一致性检测规则,在降低通信量与计算量的同时,有效而简便地检测了融合中心一致性. 新机制能有效遏制谎报攻击,改善异常节点数占有比重大时的网络性能,让融合值更贴近真实值. 理论分析及仿真证实了新机制的可靠性与有效性.
To cope with the problem captured nodes causing the deviation, the situation data fusion mechanism based on trust was presented. It makes trust awareness rule based on historical trust or data correlation, and guarantees consistency in three stages. Firstly, in event detection, after collecting data, it detects events through most trust majority rule to enhance accuracy. Secondly, during data fusion, it uses data filter rule to improve reliability. Finally, in consistency detection, it utilizes the consistency detection rule to reduce communication traffic, simultaneously judging the consistence of centers. The new mechanism can suppress misrepresentation and enhance the performance when abnormity is more than normal ones. It can also reduce the deviation between real value and fusion data. Simulation verifies the reliability and validity.
态势感知[1]是对状态或趋势进行感知,可实现网络态势的管理与评估,要素数据信息[2]的采集主要来源于传感网络. 传感网络受能源与存储容量限制,P2P、Ad hoc等参与融合,也注定网络具有开放性、脆弱性等性质. 这为敌手俘获节点创造条件,其引起融合值偏离主要方式[3]包括篡改终端数据、隐瞒终端数据、伪造中心融合数值.
现有基于信任的态势数据融合机制,较少考虑信任历史值,忽略了时间衰减性与节点数据相关度,缺少检测节点可靠性的规则. 融合时,或数据融合权值相同,或融合权值固定,但实际网络数据往往随着环境动态变化. 对于中位数融合算法[4](MFR,median aggregation rule)、平均函数融合算法[5](AFR,average fusion rule)、异构神经元融合算法[6](BPR,heterogeneous fusion processing rule)等数据融合方法,MFR可靠性最优,AFR最简单易计算但得到的融合值与实际值差距较大.
针对上述问题,在终端与中心节点均可被俘获的情况下,考虑信任的相关性和时间衰减性,笔者设计出一种基于信任的态势数据融合机制(SDFT,situation data fusion mechanism based on trust),该机制能有效遏制谎报攻击,让融合值更贴近真实值.
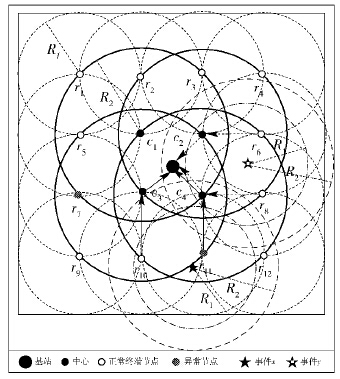
1 系统网络模型设系统中存在基站、融合中心与终端节点. 基站可与所有节点通信,能处理并存储数据;中心可收集并处理数据;终端只收集数据. 组网模型如图1所示,终端节点r1,r2,r5、r3,r4,r6、r7,r9,r10、r8,r11,r12分别属于融合中心c1、c2、c3、c4. 事件x与y同时发生,y的相关节点为r6、r8、c2、c4,x的相关节点为r10、r11、c4. 中心c4可检测事件x与y. 若事件发生在节点传感检测范围内,则该节点为事件相关节点. 若相关节点中存在中心节点,则中心直接为事件相关中心,如c2、c4对y. 若相关节点中无中心节点,则选取相关节点的上层中心为事件相关中心,如c3对x. 所有节点构成集Z′.
2 SDFTSDFT先后分3个阶段实现数据融合. 事件检测阶段,用最可信多数规则(MMR,most trust majority rule)判定事件是否发生. 数据融合阶段,若单个事件发生,则启动数筛选规则处理;若多个事件发生,先对比优先级再进行数据预处理. 一致性检测阶段,用一致性检测规则(CDR,consistency detection rule)验证中心可靠性,发布最终融合值.
2.1 事件检测事件检测阶段用于确定事件是否已发生. 事件发生,令事件状态为1;事件未发生,令事件状态为0. 目前判定事件是否发生有“与”规则、“或”规则和多数规则(GMR,general majority rule). “与”规则:有一个节点判定事件未发生,状态为未发生;“或”规则:有一个节点判定事件发生,状态为发生;GMR[7]:超过半数或半数节点认为事件发生超过半数及以上节点认为事件发生,状态为发生. SDFT用MMR判定事件是否发生,可减少系统被攻击成功的概率. 设节点检测误差范围为(-ε,ε),发生事件集为E′=[e1,e2,…,ew′]. 设对于事件e,可能相关的节点数为N′e,对应相关节点矩阵nN′e×1,则N′=[nN′1×1,…,nN′e×1,…,nN′w×1]为E′的可能相关节点矩阵. 首先,信任筛选,筛选函数为f:$ \vartheta $ (θi,e)→[0, 1],i∈N′,e∈E′,若θi,e>$ \hat \theta $,$ \hat \theta $为信任筛选门限,则$ \vartheta $(θi,e)=1,否则为0,θi,e∈[0, 1]为节点i对事件e可信度;其次,个体检测,检测函数为f:δi,e→[0, 1],若i认为e发生则δi,e=1,否则为0;最后,系统依nN′e×1中可信节点检测判定e发生状态:
| $ \begin{array}{*{20}{c}} {even{t_e} = }\\ {\left\{ \begin{array}{l} 1,\sum\limits_{i \in N'} {{\theta _{i,e}}{\delta _{i,e}} \times \vartheta \left( {{\theta _{i,e}}} \right) > \sum\limits_{i \in N'} {{\theta _{i,e}}\left( {{\rm{1 - }}{\delta _{i,e}} \times \vartheta \left( {{\theta _{i,e}}} \right)} \right) > } } \\ 0,{\rm{其他}} \end{array} \right.} \end{array} $ | (1) |
若节点i检测与系统判决一致且信任高于 A$ \hat \theta $U2 ,则纳入相关节点矩阵N=[nN1×1,…,nNe×1,…,nNw×1],Ne为相关节点数. 确已发生事件集E=[e1,e2,…,ew],优先级集Π=[ρ1,…,ρe,…,ρw]1×w,ρe∈(0,1),w为确已发生事件数. 图1模型中E=[x,y],N=[nN1×1,nN2×1],nN1×1=[r10,r11,c4]T,nN2×1=[r6,r8,c2,c4]T.
定理1 若恶意节点被MMR筛选出来的概率为l>0,则MMR的被攻击成功平均概率PFM小于或等于GMR的被攻击成功平均概率PFG,即PFM≤PFG.
证明 对同时发生的w个事件进行联合检测[8]的错误检测概率为
| $ {p_f} = P\left\{ {1/w\sum\limits_{k = 1}^w {S_k^2 > \eta } } \right\} = 1 - P\left\{ {\sum\limits_{k = 1}^w {S_k^2 \le w\eta } } \right\} $ | (2) |
其中:S2k为噪声方差,η为判决门限,$ \sum\limits_{k = 1}^w {S_k^2} $为自由度w的卡方分布. 累积分布为χF2(·),pf=1-χ2w(wη),正确检测概率为1-pf>0.5. 设恶意节点数为X,入局GMR节点数H,入局MMR节点数F=H-Xl<H,得MMR被攻击成功的平均概率:
| $ {{P}_{FM}}=\sum\limits_{\begin{smallmatrix} q=F/2 \\ F=H-XL \end{smallmatrix}}^{F}{\left( \begin{align} & F \\ & q \\ \end{align} \right)}{{\left( 1-{{p}_{f}} \right)}^{F-q}}{{\left( {{p}_{f}} \right)}^{q}} $ | (3) |
其中pf为误检概率,将pf=1-χ2w(wη)代入式(3)得
| $ {{P}_{FM}}=\sum\limits_{\begin{smallmatrix} q=F/2 \\ F=H-XL \end{smallmatrix}}^{F}{\left( \begin{align} & F \\ & q \\ \end{align} \right)}{{\left( \chi _{w}^{2}\left( w\eta \right) \right)}^{F-q}}{{\left( 1-\chi _{w}^{2}\left( w\eta \right) \right)}^{q}} $ | (4) |
同理,可得GMR被攻击成功的平均概率为
| $ {P_{FG}} = \sum\limits_{q = H/2}^{R = X} {\left( \begin{array}{l} H\\ q \end{array} \right)} {\left( {\chi _w^2\left( {w\eta } \right)} \right)^{H - q}}{\left( {1 - \chi _w^2\left( {w\eta } \right)} \right)^q} $ | (5) |
当X<H/2时,PFM=PFG=0;当X=H/2时,$ {P_{FM}} = 0 < {P_{FG}} = \left( \begin{array}{l} H\\ q \end{array} \right){\left( {1 - p} \right)^{H - q}}{\left( p \right)^q} $;当H/2<X≤H时,F=H-Xl<H,$ f\left( F \right) = \sum\limits_{q = 0}^{F/2 - 1} {\left( \begin{array}{l} F\\ q \end{array} \right)} {\left( {1 - p} \right)^{F - q}}{\left( p \right)^q} $为减函数,得PFM<PFG. 因此,PFM≤PFG.
2.2 态势数据融合数据融合的对象为具体数据,若发生事件为火灾,数据对应为温度与烟雾浓度. SDFT机制的融合步骤包含选定事件、筛选数据与融合数据.
步骤1 选定事件:若单个事件发生,节点数据直接进入数据筛选;若多个事件同时发生,基站将用优先级判别规则决定事件处理的先后顺序.
定义1 优先级判别规则:若同时发生多个事件,则集E内有多个元素,选取优先级权重最大的事件 $ e = \mathop {\max }\limits_{i \in E} {I_i} $做优先处理,其中 $ {I_i} = {\rho _i}/\sum\limits_{v \in E} {{\rho _v},{\rho _i},{\rho _v}} \in \Pi . $
步骤2 筛选数据:根据数据筛选规则,对融合数据进行预处理,选出可靠的节点数据.
定义2 数据筛选规则:对事件e,若nNe×1内所有节点共隶属于L个相关融合中心Av(v=1,2,…,L),则将L个中心组成相关中心集Ce=A1,…,Av,…,AL. nNe×1内所有隶属于中心Av∈Ce的节点组成可检测集Ov,e(v=1,2,…,L). 对任意节点i∈Ov,e,若满足条件1:|di-dOv,emed|≤Δd(di为节点i的数据,dOv,emed为Ov,e中所有节点数据的中位数,Δd为数据相关度量差值),则i被允许进入步骤3,否则以概率1-ε拒绝.
经步骤2后Ov,e内满足条件1的节点组成集Jv,e,Ov,e内可进入数据融合的节点组成可融合集Tv,e. 记录Ov,e内元素个数为mv,e,若Av∈Ce的相关节点中有Mv,e个节点满足条件1,则Jv,e内有Mv,e个元素,Tv,e内有 $\;\left\lfloor {{M_{v,e}} + \left( {{m_{v,e}} - {M_{v,e}}} \right)\varepsilon } \right\rfloor $个元素. 系统模型中y的相关中心集为Ce={c2,c4}={A1,A2},可检集为O1,y={c2,r6}、O2,y={c4,r8}. 因y的可检测范围内无异常节点,得dO1,ymed=(dc2+dr6)/2,T1,y=O1,y,T2,y=O2,y,dO2,ymed=(dc4+dr8)/2.
步骤3 融合数据:用融合规则得出中心融合值.
定义3 数据融合规则:将预融合数据根据均衡原理乘以反函数γi: $ f\left( x \right) = \sqrt {2\pi } \sigma \exp \left\{ {{{\left( {x - u} \right)}^2}/2{\sigma ^2}} \right\} $(u为数据真实值,σ为噪声方差)得归一化数值. 依据Tv,e内节点数据与可信度,得Av融合值为
| $ {d_{{A_{v,}}e}} = \frac{{\sum\limits_{i \in {T_{v,e}}} {{\theta _{i,e}}{d_i}} }}{{\sum\limits_{i \in {T_{v,e}}} {{\theta _{i,e}}} }} $ | (6) |
其中,di为隶属于相关融合中心Av的节点i数据,θi,e为节点i对事件e的可信度. 根据可信度θAv,e(Av∈Ce),可得出Av中心融合值为
| $ {b_e} = \frac{{\sum\limits_{{A_v} \in {C_e}} {{\theta _{{A_{v,}}e}}{d_{{A_{v,}}e}}} }}{{\sum\limits_{{A_v} \in {C_e}} {{\theta _{{A_{v,}}e}}} }} $ | (7) |
在系统模型中,对事件y,可得
dA1,y=(θc4,ydc4+θr8,ydr8)/(θc4,y+θr8,y)
dA2,y=(θc2,ydc2+θr6,ydr8)/(θc2,y+θr6,y)
by=(θA1,ydA1,y+θA2,ydA2,y)/(θA1,y+θA2,y)
2.3 一致性检测定义4 CDR:基站收到Ce内中心的数值后,随机抽取对应中心下层λ个节点发送数据,λ个节点组成集Se并形成融合值ge=med[di](i∈Se). 若|ge-be|<Δa(Δa为度量差值),则基站认为Ce的所有相关中心可信并将be作为事件e的融合值,否则重复进行检测. 若重复κ次仍失败,则降低不满足条件2:be-med[dAv,e]<Δa(Av∈Ce)的相关中心可信度并将ge作为最终融合值,dAv,e为Av∈Ov,e的融合数据,med[dAv,e]为dAv,e的中位数.
SDFT用CDR随机采样对中心进行检测. 全局搜索检测法(GAS,global all search detection) 检测所有节点以验证中心可靠性. 设检测节点总数为Q,采样点数为U<Q,则复杂度:GAS为Ο(Q2+Q/2)、CDR为Ο(UQ+Q/2),前后比值为Q/U;可靠性:GAS小于且接近1、CDR为1-CikCm-in-k/Cmn.
2.4 可信度感知准则SDFT机制根据时间衰减性与数据相关性,按照节点报送的事件数据调整可信度. 非相关节点保持参数不变. 若系统检测出终端异常,则降低终端可信度0.1;若检测出中心异常,则降低中心可信度0.2. 初始设终端可信度为0.8,中心可信度为1.0. 因异常行为被剔除的节点,需待处理5次事件后可重回系统. 每执行融合20次,所有节点可信度重回初始值. 可信度准则1)、2)、4)适用于终端与中心节点,准则3)仅适用于中心节点. 对事件e,可信度感知准则如下.
1) 事件检测阶段,相关节点个体检测后输出事件状态值与系统判决的状态值不一致,则把该节点可信度减低Δθ,其他节点可信度保持不变.
2) 数据融合步骤2中Ov,e内任意节点i不满足条件1,则将其可信度更新为θi,e=θi,e-0.1.
3) 一致性检测阶段,基站对比be与ge,若满足条件ge-be<Δa,则保持Ce内相关中心的可信度不变;若不满足条件且重复κ次检测仍不失败,则将Ce内不满足条件2:be-med[dAv,e]<Δa的中心Av∈Ce可信度降低,更新为θAv,e=θAv,e-0.2.
4) 发布最终融合数据后,机制根据节点信任与数据相关度微调可信度. 对于参与步骤3的所有节点,令任意两节点i,q∈Tv,e的数据相关度为ξiq,若满足条件di-dq<Δa,则ξiq=1,否则ξiq=0. 若节点i∈Tv,e历史可信度为θi,时间衰减因子为μ,则完成事件e数据融合后,节点i可信度更新为
| $ {\theta _{i,e}} = \mu {{\tilde \theta }_i} + \frac{{\left( {1 - \mu } \right)}}{{{M_{v,e}} + \left( {{m_{v,e}} - {M_{v,e}}} \right)\varepsilon }}\sum\limits_{q = 1}^{\left\lfloor {{M_{v,e}} + \left( {{m_{v,e}} - {M_{v,e}}} \right)\varepsilon } \right\rfloor } {{\xi _{iq}}} $ | (8) |
为评估上述机制性能,现根据理论构架进行仿真验证,考虑传输中的路径损耗和阴影衰落. 设网络在中等城市区域传输通信,传感节点最大发射功率为19dBm,载波频率为2.4GHz,传感节点天线高度为1m,节点天线增益为2.15dBi;基站天线有效高度为10m,基站天线增益为11dBi. 根据3GPP TS25. 102标准的多径衰落模型与阴影衰落建模方法[9]进行仿真,设96个终端节点、4个融合中心与1个基站均匀分布在110m×110m区域内,相邻节点间距为1m,终端传感半径为1m,中心传感半径大于 $ 2\sqrt 2 $m. 数据筛选条件1中 A$ \hat \theta $U2 =0.3,μ=0.3. 可信度感知准则1)中Δθ=0.1,数据筛选差值Δd与检测差值Δa均为5. 一致性检测最大重复次数κ=10,采样数λ=20. 以下选择MFR[4]、AFR[5]、BPR[6]与SDFT做比对,使用推荐参数与推荐基函数进行计算.
3.1 机制融合值与真实值偏离程度评估因不确定性因素影响,机制无法避免地会存在偏离误差. 用毁坏程度衡量机制融合值与真实值的差异,毁坏程度越大则融合值与真实值差异越大;反之,差异越小. 衡量指标为平均绝对毁坏程度百分比λ:
| $ \lambda = \frac{1}{N}\sum\limits_{n = 1}^N {\left| {\frac{{fusio{n_n} - real}}{{\max \left( {real,fusio{n_n}} \right)}}} \right|} $ | (9) |
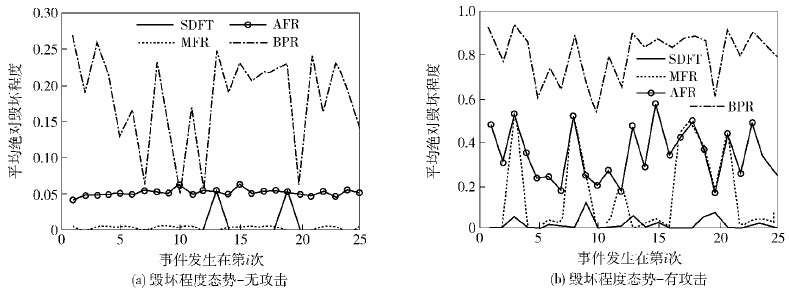
其中:fusionn为第n次融合值,real为真实值,N为融合次数. 仿真针对加法与平方类型窜改攻击,在无攻击与有攻击的情况下运行SDFT、AFR[5]、BPR[6]与MFR[4]25次后求平均得到毁坏程度态势如图2所示. 由图2(a)可知,无攻击时,MFR毁坏程度最低,事件13、19处有凸起,因一致性检测时下层未通信节点被采样,造成数据毁坏程度增加. 图2(b)为存在攻击时的毁坏程度态势,SDFT的MADDP最低,因在第3、8、13、15、18事件处有攻击存在,4种规则毁坏程度相应增高. 由此可知,无攻击时MFR毁坏程度最低,有攻击时SDFT毁坏程度最低.
3.2 机制稳定性评估机制稳定性以最小均方误差作为评估标准,均方误差越小,系统越稳定. 因SDFT能滤除异常节点,可降低均方误差. 根据图2(b)中SDFT、MFR[4]、AFR[5]与BPR[6]有攻击情况下的MADDP,分别得均方误差0.026、0.073、0.144、0.652,稳定性性能如表1所示.
| 表1 稳定性性能 |
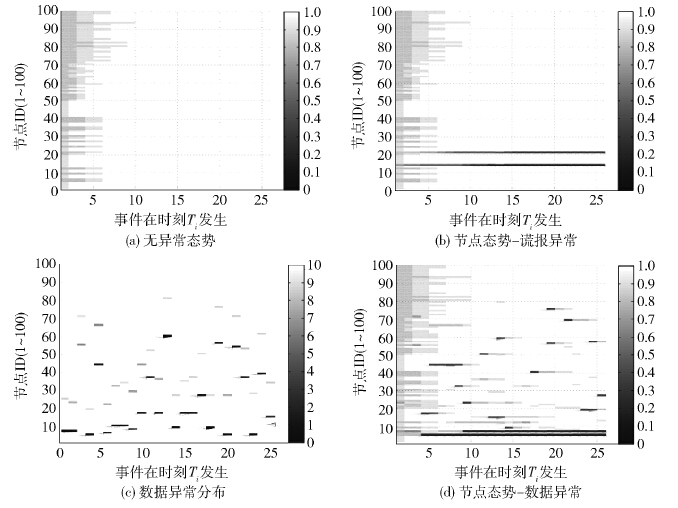
机制依据节点可信度及相关度进行信任态势评估,把节点可信度分别按取值范围[0.0,0.3)、[0.3,0.5)、[0.5,0.8)、[0.8,1.0]分为A、B、C、D 4个可信等级,分别表示不可信、近似可信、近似不可信与可信,并规定节点可信度为B及以上等级可参与融合. SDFT根据事件发生顺序,仿真得到可信度态势如图3.
图3(a)为机制仿真25个无攻击事件得到的可信度态势,图左上角灰色区域表示学习过程. 图3(b)为机制仿真25个事件在节点14、21处存在谎报的可信度态势,第14与21节点总谎报,因而可信度从0.8降到0.3,低于可信度门限0.3则被剔除. 图3(c)为视化节点对25个事件提供的数据异常情况得到的态势,其中灰色区域表示节点在对应事件处近似异常,而白色区域表示可信,黑色表示异常. 机制处理图3(c)中的事件数据后得图3(d)异常节点的可信度态势. 对比图3(c)可知,图3(d)中显示出节点7、10、23处存在连续多次异常,节点30、31、32处存在偶发异常,态势视化存在遗漏,但态势图对谎报异常与数据连续异常能较准确地反映节点态势分布情况.
4 结束语针对无线传感网络中节点被俘获而导致融合值偏离的问题,提出了一种SDFT机制. 理论分析了该机制功能的具体实现,仿真验证了该机制降低了被攻击成功的概率,在恶意节点存在的情况下,减少了融合值与真实值的偏离程度.
| [1] | Coronato A, Pietro G. Situation awareness in applications of ambient assisted living for cognitive impaired people[J]. Mobile Networks and Applications, 2013, 18(3): 444-453.[引用本文:2] |
| [2] | Dong X, Srivastava D. Big data integration[C]//International Conference on Very Large Data Bases. Brisbane: IEEE Press, 2013: 1245-1248.[引用本文:1] |
| [3] | Dietzel S, Schoch E, Konings B, et al. Resilient secure aggregation for vehicular network[J]. IEEE Networks, 2010, 24(1): 26-31.[引用本文:1] |
| [4] | Wagner D. Resilient aggregation in sensor networks[C]//ACM Workshop on Security of Ad hoc and Sensor Networks. Washington: ACM Press, 2004: 78-87.[引用本文:4] |
| [5] | Bohili J, Papadimitratos P, Verardi D, et al. Resilient data aggregation for unattended WSNs[C]//IEEE International Workshop on Practical Issues in Building Sensor Network Applications. Bonn: IEEE Press, 2011: 994-1002.[引用本文:4] |
| [6] | Liu Xiaowu, Yu Jiguo, Wang Maoli. Network security situation generation and evaluation based on heterogeneous sensor fusion[C]//International Conference on Wireless Communnications, Networking and Mobile Computing. Beijing: IEEE Press, 2009: 1-4.[引用本文:4] |
| [7] | 闫琦, 杨家玮, 张雯. 认知无线电网络中安全的合作频谱感知[J]. 北京邮电大学学报, 2011, 34(2): 71-75. Yan Qi, Yang Jiawei, Zhang Wen. The sensing of the secure cooperative spectrum in cognitive radio networks[J]. Journal of Beijing University of Posts and Telecommunications, 2011, 34(2): 71-75.[引用本文:1] |
| [8] | Thomas C, Kewal K, Parameswaran R. Fault tolerance in collaborative sensor networks for target detection[J]. IEEE Transactions on Computers, 2004, 53(3): 320-333.[引用本文:1] |
| [9] | Cai Xiaodong, Giannakis G. A two-dimensional channel simulation model for shadowing processes[J]. IEEE Transactions on Vehicular Technology, 2003, 52(6): 1558-1567.[引用本文:1] |